Applied Statistics Assignment: Golf Score Data Analysis and Regression

This assignment provides a comprehensive statistical analysis of golf scores, comparing performance with original and new clubs. It begins with a scatter plot analysis to visualize the relationship between scores, followed by the calculation and interpretation of the correlation coefficient, demonstrating a positive and moderately strong linear relationship. The solution then constructs a regression model, determining the least squares regression line, slope coefficient, and SSE. Predictions for new scores are made based on old scores. Further, the assignment delves into hypothesis testing for the slope coefficient, using confidence intervals to assess its significance. The coefficient of determination is computed to explain the variation in golf scores. Finally, the document calculates point estimates and confidence intervals for a golfer's scores using the new clubs, illustrating the application of statistical concepts in real-world scenarios.

APPLIED STATISTICS
STUDENT ID:
[Pick the date]

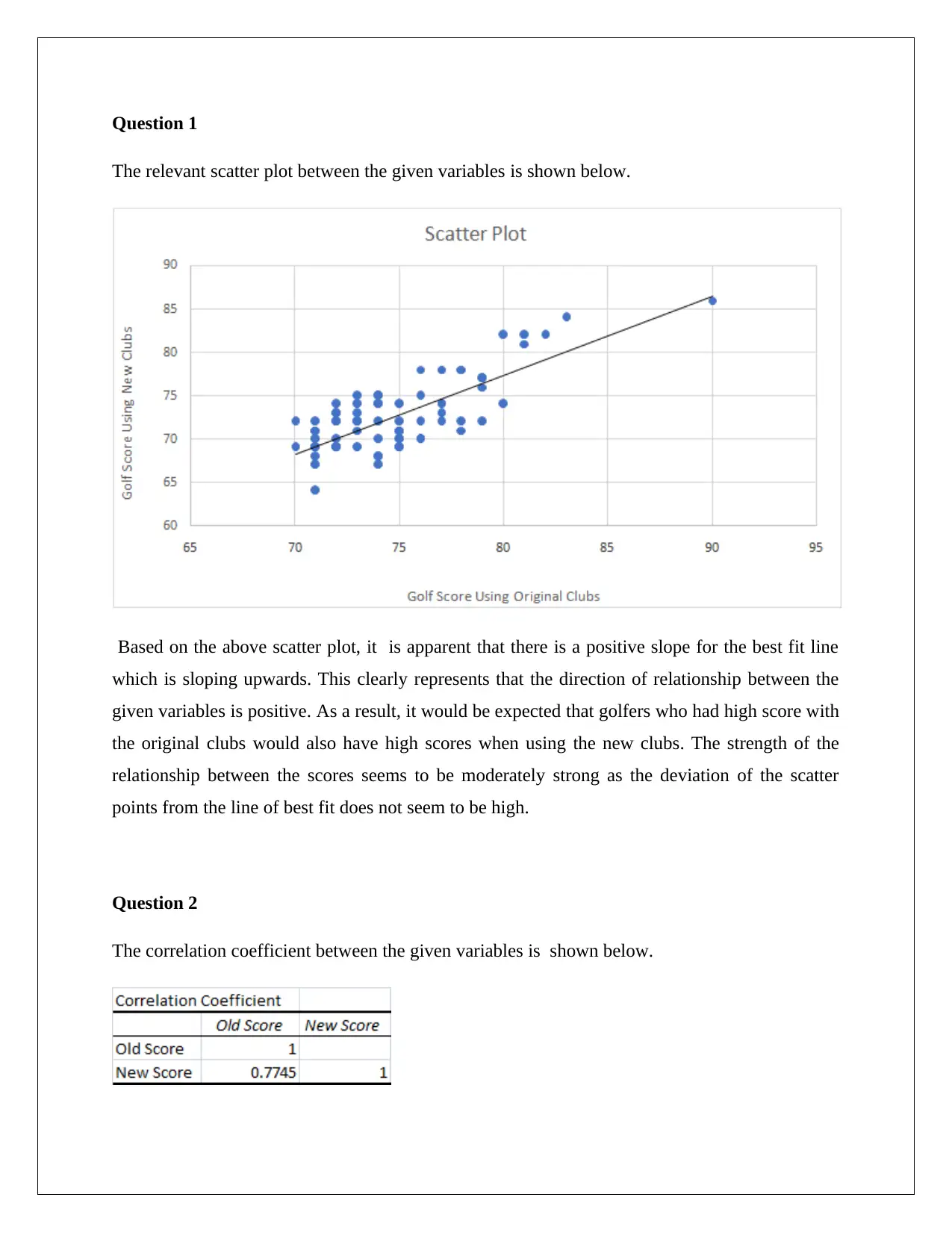
Question 1
The relevant scatter plot between the given variables is shown below.
Based on the above scatter plot, it is apparent that there is a positive slope for the best fit line
which is sloping upwards. This clearly represents that the direction of relationship between the
given variables is positive. As a result, it would be expected that golfers who had high score with
the original clubs would also have high scores when using the new clubs. The strength of the
relationship between the scores seems to be moderately strong as the deviation of the scatter
points from the line of best fit does not seem to be high.
Question 2
The correlation coefficient between the given variables is shown below.

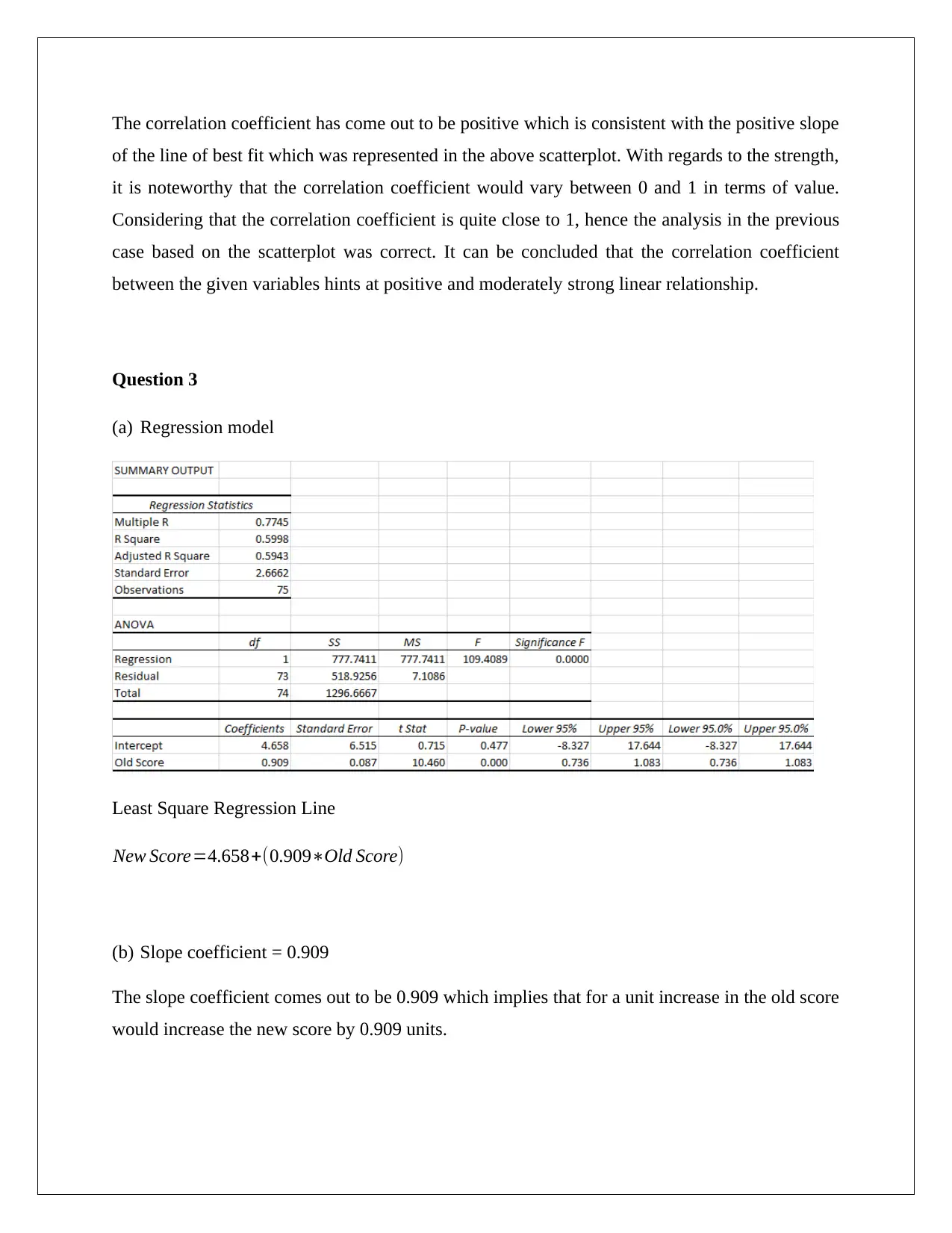
The correlation coefficient has come out to be positive which is consistent with the positive slope
of the line of best fit which was represented in the above scatterplot. With regards to the strength,
it is noteworthy that the correlation coefficient would vary between 0 and 1 in terms of value.
Considering that the correlation coefficient is quite close to 1, hence the analysis in the previous
case based on the scatterplot was correct. It can be concluded that the correlation coefficient
between the given variables hints at positive and moderately strong linear relationship.
Question 3
(a) Regression model
Least Square Regression Line
New Score=4.658+(0.909∗Old Score)
(b) Slope coefficient = 0.909
The slope coefficient comes out to be 0.909 which implies that for a unit increase in the old score
would increase the new score by 0.909 units.

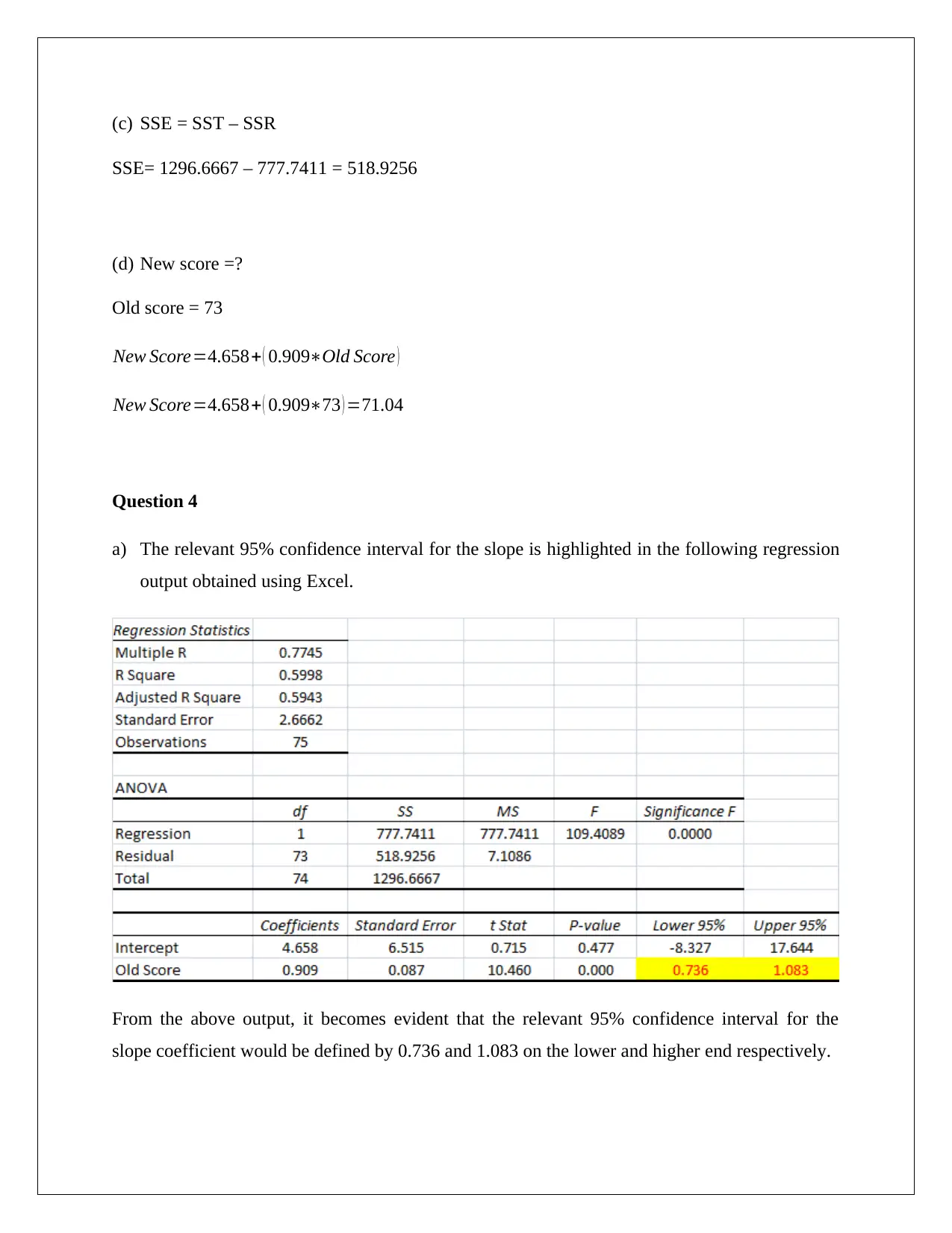
(c) SSE = SST – SSR
SSE= 1296.6667 – 777.7411 = 518.9256
(d) New score =?
Old score = 73
New Score=4.658+ ( 0.909∗Old Score )
New Score=4.658+ ( 0.909∗73 ) =71.04
Question 4
a) The relevant 95% confidence interval for the slope is highlighted in the following regression
output obtained using Excel.
From the above output, it becomes evident that the relevant 95% confidence interval for the
slope coefficient would be defined by 0.736 and 1.083 on the lower and higher end respectively.

b) The relevant hypothesis testing for the slope coefficient is carried out based on the following
hypothesis.
Null Hypothesis (H0): βold score = 1
Alternative Hypothesis (H1): βold score ≠1
The significance level for the test has been assumed as 10% or 0.1.
The hypothesis testing in this case would be performed using the confidence interval approach.
The decision rule as per this approach is that null hypothesis would be rejected only when the
hypothesized value does not lie in the relevant confidence interval.
The computation of the 90% confidence interval for the slope is shown below.
Mean value of slope = 0.909 (From regression output)
Standard error = 0.087 (From regression output)
T critical value with df = 74 and 90% confidence level is +/- 1.6657
Lower limit of 90% confidence interval of slope = 0.909*-1.6657*0.087 = 0.764
Higher limit of 90% confidence interval of slope = 0.909*+1.6657*0.087 = 1.054
The 90% confidence interval for the slope under testing is (0.764,1.054). It is apparent that the
hypothesized value of 1 is included in the confidence interval. As a result, the available evidence
is not sufficient to reject the null hypothesis and accept the alternative hypothesis. As a result, it
may be concluded that the slope value does not significantly differ from 1.
Question 5
The coefficient of determination is the square of the underlying correlation coefficient. Hence,
the computation of this is indicated below.
Coefficient of determination = (0.7745)2 = 0.5998

The above value implies that 59.98% of the variation in the dependent variable (i.e. new score)
can be explained on account of corresponding variation in the independent variable (i.e. old
score). Also, 40.02% of the variation in the new score cannot be explained by the variation in the
old score. As a result, other useful predictor variables would need to be inserted in the given
regression model so as to improve predictive power.
Question 6
a) The point estimate of Thurio’s scores in round 1 using the new club can be computed using
the regression equation derived which is listed below.
New Score=4.658+ ( 0.909∗Old Score )
New Score=4.658+ ( 0.909∗72 ) =70.13
b) The interval evaluated for this problem would be a confidence interval and not prediction
interval. This is because it would consider only the uncertainty associated with the mean of
the population and not with any uncertainty regarding the data scatter. The prediction interval
takes both the factors into consideration and is thereby wider.
c) In order to compute the 90% confidence interval of Thurio’s score in round one, it would be
necessary to estimate the 90% confidence interval of the regression coefficients.
The 90% confidence interval for the slope under testing is (0.764,1.054). This has been estimated
in question 4
The 90% confidence interval computation for the intercept coefficient is shown below.
Mean value of intercept coefficient = 4.658 (From regression output)
Standard error = 6.515 (From regression output)
T critical value with df = 74 and 90% confidence level is +/- 1.6657
Lower limit of 90% confidence interval of intercept coefficient= 4.658 -1.6657*6.515 = -6.195

Higher limit of 90% confidence interval of intercept coefficient = 4.658+1.6657*6.515= 15.511
Lower limit of 90% confidence interval for Thurio’s score = -6.195 + 0.764*72 = 48.81
Higher limit of 90% confidence interval for Thurio’s score =15.511 + 1.054*72 = 91.4