Physics Project: Gravitational Acceleration Experiment Analysis

This physics project investigates gravitational acceleration through a free-fall experiment. The student analyzes experimental data, calculates gravitational acceleration (g) for various celestial bodies (Callisto, Larissa, Earth, Io, Ceres), and determines associated errors. The project includes the derivation of the formula for g, calculations of range and maximum height of a projectile, and estimations of the mass and radius of planets and moons based on escape velocity. The student discusses potential sources of error, compares calculated values with theoretical values, and provides a comprehensive analysis of the experiment, including the impact of various factors on the results. The project provides a detailed look at the concepts of gravitational acceleration and its application in physics.

Gravitational Acceleration Experiment – Individual Investigation 1
GRAVITATIONAL ACCELERATION EXPERIMENT – INDIVIDUAL INVESTIGATION
Name
Course
Professor
University
City/state
Date

Gravitational Acceleration Experiment – Individual Investigation 2
Gravitational Acceleration Experiment – Individual Investigation
Part A
The validity of the formula g= 8 H
T 22 −T 1² is investigated using the experimental results obtained
using free fall method. The results are provided in Table 1 below
Table 1: experimental results
Moon/planet Height (m) Time (s) H (m) T2² – T1² g (m/s2)
Callisto 0.61 0.95 0.20 0.7875 2.03
Larissa 0.81 1.30 0.19 0.4356 3.49
Earth 1 1.12 0.29 0.4444 5.22
Io 0.71 0.90 0.24 0.3744 5.13
Ceres 0.47 0.66 0.14 0.4669 2.40
The values of H and T22 – T12 can be used to plot a graph of T22 – T12 against 8 H
g . The graph is
expected to be linear with its slope being equivalent to 8
g . Using the experimental results
obtained, the graph of T22 – T12 against 8 H
g is provided in Figure 1 below.

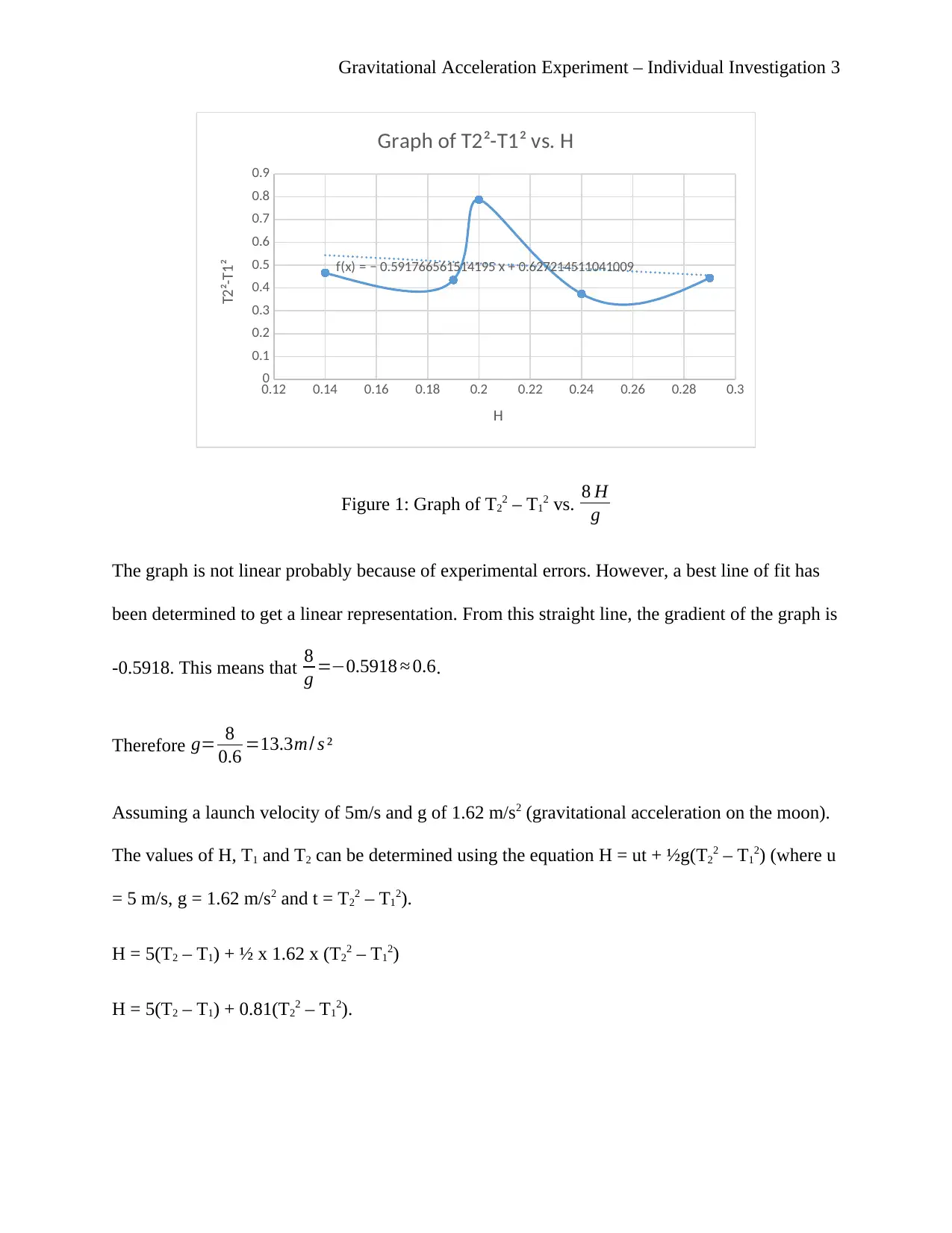
Gravitational Acceleration Experiment – Individual Investigation 3
0.12 0.14 0.16 0.18 0.2 0.22 0.24 0.26 0.28 0.3
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
f(x) = − 0.591766561514195 x + 0.627214511041009
Graph of T2²-T1² vs. H
H
T2²-T1²
Figure 1: Graph of T22 – T12 vs. 8 H
g
The graph is not linear probably because of experimental errors. However, a best line of fit has
been determined to get a linear representation. From this straight line, the gradient of the graph is
-0.5918. This means that 8
g =−0.5918 ≈ 0.6.
Therefore g= 8
0.6 =13.3m/ s ²
Assuming a launch velocity of 5m/s and g of 1.62 m/s2 (gravitational acceleration on the moon).
The values of H, T1 and T2 can be determined using the equation H = ut + ½g(T22 – T12) (where u
= 5 m/s, g = 1.62 m/s2 and t = T22 – T12).
H = 5(T2 – T1) + ½ x 1.62 x (T22 – T12)
H = 5(T2 – T1) + 0.81(T22 – T12).

Gravitational Acceleration Experiment – Individual Investigation 4
In general the formula for gravitational acceleration is formula g= 8 H
T 22 −T 1² . This means that
when H is fixed, a smaller value of g than 9.8 m/s2 will result to an increase in the difference
between T12 and T22, and a larger value of g than 9.8 m/s2 will result to a decrease in the
difference between T12 and T22. This is because when H is fixed, the difference between T12 and
T22 is inversely proportional to g.
Calculating g and Δg
Calculations of g:
The values of g are calculated using the equation ¿ 8 H
T 22−T 1² as follows:
Callisto moon: g= 8 x (0.81 m−0.61 m)
1.30 s ²−0.95 s ² = 8 x 0.2 m
0.7875 s ² =2.03 m/s ²
Larissa moon: g= 8 x (1 m−0.81 m)
1.30 s ²−1.12 s ² = 8 x 0.19 m
0.4356 s ² =3.49 m/ s ²
Earth: g= 8 x (1 m−0.71 m)
1.12 s ²−0.90 s ² = 8 x 0.29 m
0.4444 s ² =5.22m/ s ²
Io moon: g= 8 x (0.71 m−0.47 m)
0.90 s ²−0.66 s ² = 8 x 0.24 m
0.3744 s ² =5.13 m/ s ²
Ceres moon: g= 8 x (0.61 m−0.47 m)
0.95 s ²−0.66 s ² = 8 x 0.14 m
0.4669 s ² =2.39 m/ s ²
Calculations of Δg:
When ΔH = 0.001, ΔT1 = 0.1 and ΔT2 = 0.1

Gravitational Acceleration Experiment – Individual Investigation 5
The values of Δg are calculated using the equation Δg=g ( ΔH
H + 2T 1 ΔT 1
T 22−T 12 + 2T 2 ΔT 2
T 22−T 12 ) as
follows:
Callisto moon: Δg=2.03 ( 0.001
0.2 + 2 x 0.95 x 0.1
1.3²−0.95² + 2 x 1.3 x 0.1
1.3²−0.95² )=2.03 ( 0.005+0.24+ 0.33 ) =1.17
Larissa moon: Δg=3.49 ( 0.001
0.19 + 2 x 1.3 x 0.1
1.3²−1.12² + 2 x 1.12 x 0.1
1.3²−1.12² )=3.49 ( 0.0053+ 0.60+0.51 )=3.89
Earth: Δg=5.22 ( 0.001
0.29 + 2 x 1.12 x 0.1
1.12²−0.9² + 2 x 0.9 x 0.1
1.12²−0.9² )=5.22 ( 0.0034+ 0.50+0.41 )=4.77
Io moon: Δg=5.13 ( 0.001
0.24 + 2 x 0.9 x 0.1
0.9²−0.66² + 2 x 0.66 x 0.1
0.9²−0.66² )=5.13 ( 0.0042+0.48+0.35 )=4.28
Ceres moon: Δg=2.39 ( 0.001
0.14 + 2 x 0.95 x 0.1
0.95²−0.66² + 2 x 0.66 x 0.1
0.95²−0.66² )=2.39 ( 0.0071+0.41+0.28 )=1.67
When ΔH = 0.001, ΔT1 = 0.01 and ΔT2 = 0.01
The values of Δg are calculated using the equation Δg=g ( ΔH
H + 2T 1 ΔT 1
T 22−T 12 + 2T 2 ΔT 2
T 22−T 12 ) as
follows:
Callisto moon:
Δg=2.03 ( 0.001
0.2 + 2 x 0.95 x 0.01
1.3²−0.95² + 2 x 1.3 x 0.01
1.3²−0.95² )=2.03 ( 0.005+0.024+ 0.033 )=0.13
Larissa moon: Δg=3.49 ( 0.001
0.19 + 2 x 1.3 x 0.01
1.3²−1.12² + 2 x 1.12 x 0.01
1.3²−1.12² )=3.49 ( 0.0053+ 0.06+0.05 ) =0.40

Gravitational Acceleration Experiment – Individual Investigation 6
Earth: Δg=5.22 ( 0.001
0.29 + 2 x 1.12 x 0.01
1.12²−0.9² + 2 x 0.9 x 0.01
1.12²−0.9² )=5.22 ( 0.0034+0.05+0.041 )=0.49
Io moon: Δg=5.13 ( 0.001
0.24 + 2 x 0.9 x 0.01
0.9²−0.66² + 2 x 0.66 x 0.01
0.9²−0.66² )=5.13 ( 0.0042+0.048+0.035 ) =0.45
Ceres moon:
Δg=2.39 ( 0.001
0.14 + 2 x 0.95 x 0.01
0.95²−0.66² + 2 x 0.66 x 0.01
0.95²−0.66² )=2.39 ( 0.0071+0.041+0.028 ) =0.18
The summary of the calculations is provided in Table 2 below
Table 2: Summary of values of g and Δg
Trial Height
(m)
Time
(s)
g
(m/s2)
Δg1
(m/s2)
Δg2 (m/s2) Exp. g1
(m/s2)
Exp. g2
(m/s2)
Callisto 0.61 0.95 2.03 1.17 0.13 3.20 2.16
Larissa 0.81 1.30 3.49 3.89 0.40 7.38 3.89
Earth 1 1.12 5.22 4.77 0.49 9.99 5.71
Io 0.71 0.90 5.13 4.28 0.45 9.41 5.58
Ceres 0.47 0.66 2.39 1.67 0.18 4.06 2.57
From Table 2 above, the closest value to the gravitational acceleration on earth is 9.99 m/s2,
which is the gravitational acceleration for earth. Compared with theoretical g on earth, the
percent error is as follows:
% error= 9.99−9.80
9.8 x 100 %=1.94 %
This is a very small percent error meaning that the accuracy of the readings was high. However,
the g calculated from other readings is very small in comparison with the g on earth. Therefore is
it expected that g will be measured with less precision than the ones given.
Derivation of the formula for g

Gravitational Acceleration Experiment – Individual Investigation 7
One of the equations of uniform acceleration is s = ut + ½at2 [1]; where s = distance between two
points, u = initial velocity, = acceleration and t = time taken for the object to cover the distance s.
In this case, s = H, u = 0, and t = T2 – T1.
Substituting these values in the equation gives:
H = 0 + ½g(T22 – T12)
H = ½g(T22 – T12)
Making g the subject of the formula gives:
2H = g(T22 – T12)
g= 2 H
T 22 −T 1²
Part B
Calculating range
Range is calculated using the following equation: R=u2 sin 2θ
g ; where R = range, u = initial
velocity of cannonball, θ = angle of launch, and g = gravitational acceleration [2].
Take u = 10 m/s, θ = 45° → 2θ = 90°, and g = 9.8 m/s2.
R=102 x sin 90
9.8 =10.2 m
Calculating maximum height

Gravitational Acceleration Experiment – Individual Investigation 8
Maximum height is calculated using the following equation: s= u2 sin ² θ
2 g ; where s = maximum
height, u = initial velocity of cannonball, θ = angle of launch, and g = gravitational acceleration
[3].
Take u = 10 m/s, θ = 90°, and g = 9.8 m/s2.
There s= 102 x sin ² 90
2 x 9.8 =5.1m
The other aspects of the solar object that might impact the result include: shape of the object, size
of the object, mass of the object, the level from which the object is launched, and the velocity of
wind.
Calculating mass and radius of the planet/moon
The escape velocity, vesc is 10 km/s = 10,000 m/s
The escape velocity is given as: vesc = √ 2 GM
r ; making GM the subject gives:
GM =rVesc ²
2 ; where r = radius of the planet, G = universal gravitational constant, M = mass of
the planet and vesc = escape velocity of the planet.
But g is also given as: g= GM
r ² CITATION Sofnd \l 1033 [1]; making GM the subject gives:
GM = gr2; where g = gravitational acceleration of the planet, G = universal gravitational
constant, M = mass of the planet, and r = radius of the planet.
Equating the two expressions for GM gives:

Gravitational Acceleration Experiment – Individual Investigation 9
rVesc ²
2 =g r2; dividing r on both sides of the equation gives:
Vesc²
2 =gr; making r the subject gives:
r =Vesc ²
2 g ; substituting the values of vesc and g
r =(10,000)²
2 x 9.8 =5.1 x 106 m
The value of M can be obtained from the equation GM = gr2; → M = g r2
G ; substituting the values
of g, r and G gives:
M = 9.8 x ( 5.1 x 106 )
2
6.67 x 10−11 =3.82 x 1024 kg
Therefore the radius and mass of the planet is 5.1 x 106 m and 3.82 x 1024 kg respectively.
For speeds greater than the escape velocity, the cannonball will escape into space.
Radius and mass of the moons
Assuming that escape velocity for all the moons/planet is 10,000 m/s
The values of g used are the ones in the last column of Table 2 above.
Callisto moon:
g = 2.16 m/s2
r =Vesc ²
2 g ; substituting the values of vesc and g gives:

Gravitational Acceleration Experiment – Individual Investigation 10
r =(10,000)²
2 x 2.16 =23.1 5 x 106 m
M = g r2
G ; substituting the values of g, r and G gives:
M = 2.16 x ( 23.15 x 106 )
2
6.67 x 10−11 =17.3 5 x 1024 kg
Larissa moon:
g = 3.89 m/s2
r =Vesc ²
2 g ; substituting the values of vesc and g gives:
r =(10,000)²
2 x 3 . 89 =12. 8 5 x 106 m
M = g r2
G ; substituting the values of g, r and G gives:
M = 3 . 89 x ( 12. 8 5 x 106 ) 2
6.67 x 10−11 =9 .63 x 1024 kg
Earth:
g = 5.71 m/s2
r =Vesc ²
2 g ; substituting the values of vesc and g gives:
r =(10,000)²
2 x 5.71 =8 .76 x 106 m
M = g r2
G ; substituting the values of g, r and G gives:

Gravitational Acceleration Experiment – Individual Investigation 11
M = 5 .71 x ( 8 .76 x 106 ) 2
6.67 x 10−11 =6 .57 x 1024 kg
Io moon:
g = 5.58 m/s2
r =Vesc ²
2 g ; substituting the values of vesc and g gives:
r =(10,000)²
2 x 5.58 =8.96 x 106 m
M = g r2
G ; substituting the values of g, r and G gives:
M = 5 .58 x ( 8.96 x 106 ) 2
6.67 x 10−11 =6 . 72 x 1024 kg
Ceres moon:
g = 2.57 m/s2
r =Vesc ²
2 g ; substituting the values of vesc and g gives:
r =(10,000)²
2 x 2 .57 =19.46 x 106 m
M = g r2
G ; substituting the values of g, r and G gives:
M = 2.57 x ( 19 . 46 x 106 ) 2
6.67 x 10−11 =1 4 .6 x 1024 kg
The summary of radius and mass of moons is provided in Table 3 below

Gravitational Acceleration Experiment – Individual Investigation 12
Table 3: Radius and mass of the moons
Moon/plant Radius (m) Mass (kg)
Callisto moon 23.15 x 106 17.35 x 1024
Larissa moon 12.85 x 106 9.63 x 1024
Earth 8.76 x 106 6.57 x 1024
Io moon 8.96 x 106 6.72 x 1024
Ceres moon 19.46 x 106 14.6 x 1024
References
[1] G. Elert, "Equations of motion," 2019. [Online]. Available: https://physics.info/motion-equations/.
[Accessed 6 April 2019].
[2] BYJU'S, "Projectile Motion Formula," 2019. [Online]. Available: https://byjus.com/projectile-motion-
formula/. [Accessed 6 April 2019].
[3] P. Chudinov, V. Eltyshev and Y. Barvkin, "Simple analytical description of projectile motion in a
medium with quadratic drag force," Athens Journal of Natural & Formal Sciences, vol. 1, no. 2, pp.
97-106, 2014.
[4] Softschools.com, "Acceleration Due to Gravity Formula," (n.d.). [Online]. Available:
http://www.softschools.com/formulas/physics/acceleration_due_to_gravity_formula/54/.
[Accessed 7 April 2019].