Physics Group Report: Gravitational Acceleration Experiment Analysis
VerifiedAdded on 2023/01/16
|7
|1607
|86
Report
AI Summary
This group report details a physics experiment designed to determine gravitational acceleration using the free fall method. The experiment involved measuring the time it took for a ball to cross specific height markers when thrown vertically upwards. By measuring the time difference at two different heights, the gravitational acceleration (g) was calculated using a derived formula. The report includes a detailed description of the experimental procedure, materials used (stopwatch, meter stick, ball, markers), and the data collection process. The results section presents calculated values of g for different scenarios (e.g., Callisto, Larissa, Earth) along with their associated errors. The analysis section includes a graph showing the relationship between height and time and a discussion of the error analysis. The report concludes with a comparison of the experimental value of g with the theoretical value, a calculation of the percentage difference, and a discussion of potential sources of error and suggestions for improvement, such as improving measurement precision and controlling environmental factors. The report highlights the importance of accurate measurements and error analysis in experimental physics.

Gravitational Acceleration – Group Report 1
GRAVITATION ACCELERATION EXPERIMENT – GROUP EXPERIMENT
Names of Group Members
Course
University
City/state
Date
GRAVITATION ACCELERATION EXPERIMENT – GROUP EXPERIMENT
Names of Group Members
Course
University
City/state
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Gravitational Acceleration – Group Report 2
Gravitation acceleration experiment – Group Experiment
Introduction
There are different methods of determining gravitation acceleration due to gravity. The main
purpose of this experiment is to determine gravitational acceleration using free fall method. This
method is based on the fact that if a ball is thrown up vertically, it will cross a given height H1
twice – when moving up and when moving down [1]. The difference between the times when the
ball cross the given height when moving up and down is taken as T1. If the same ball is thrown
up vertically to a different height, it will also cross this particular height twice. The difference in
time when the ball crosses this particular time when moving up and down is taken as T2. The
difference between the two heights is determined as: H = H1 – H2. In this experiment it is
assumed that the only force acting on the ball when it is thrown up vertically is gravitational
force. This means that air resistance is neglected [2]. This is because the sources of friction,
which are the distance within which the ball is falling and the speed at which the ball is falling,
are small hence resistance is insignificant [3].
Using the above information, gravitational acceleration g can be calculated using equation 1
below
g= 8 H
T 22 −T 12 ………………………………………….. (1)
It is important to note that the calculation of g is not dependent on the ball’s initial velocity, vo.
In cases where the height and times have been measured with uncertainty ΔH, ΔT1 and ΔT2
respectively then the error Δg can be estimated using equation 2 below
Gravitation acceleration experiment – Group Experiment
Introduction
There are different methods of determining gravitation acceleration due to gravity. The main
purpose of this experiment is to determine gravitational acceleration using free fall method. This
method is based on the fact that if a ball is thrown up vertically, it will cross a given height H1
twice – when moving up and when moving down [1]. The difference between the times when the
ball cross the given height when moving up and down is taken as T1. If the same ball is thrown
up vertically to a different height, it will also cross this particular height twice. The difference in
time when the ball crosses this particular time when moving up and down is taken as T2. The
difference between the two heights is determined as: H = H1 – H2. In this experiment it is
assumed that the only force acting on the ball when it is thrown up vertically is gravitational
force. This means that air resistance is neglected [2]. This is because the sources of friction,
which are the distance within which the ball is falling and the speed at which the ball is falling,
are small hence resistance is insignificant [3].
Using the above information, gravitational acceleration g can be calculated using equation 1
below
g= 8 H
T 22 −T 12 ………………………………………….. (1)
It is important to note that the calculation of g is not dependent on the ball’s initial velocity, vo.
In cases where the height and times have been measured with uncertainty ΔH, ΔT1 and ΔT2
respectively then the error Δg can be estimated using equation 2 below

Gravitational Acceleration – Group Report 3
Δg=g ( ΔH
H + 2T 1 ΔT 1
T 22−T 12 + 2T 2 ΔT 2
T 22−T 12 ) ……………………………. (2)
The theoretical or numerical value of gravitational acceleration is 9.80 m/s2 [4].
Procedure
The devices and materials used in this experiment included the following: a stopwatch, meter
stick, ball and marker. Two horizontal markers were drawn on the board then the distance
between them measured carefully and recorded as ΔH. One member of the group threw a ball up
vertically then the remaining members of the group recorded the time the ball crossed the first
and second horizontal markers.
Results
The measured and calculated results from the experiment are provided in Table 1 below.
Calculations of g:
The values of g are calculated using equation 1 as follows
Callisto moon: g= 8 x (0.81 m−0.61 m)
1.30 s ²−0.95 s ² = 8 x 0.2 m
0.7875 s ² =2.03 m/s ²
Larissa moon: g= 8 x (1 m−0.81 m)
1.30 s ²−1.12 s ² = 8 x 0.19 m
0.4356 s ² =3.49 m/ s ²
Earth: g= 8 x (1 m−0.71 m)
1.12 s ²−0.90 s ² = 8 x 0.29 m
0.4444 s ² =5.22m/ s ²
Io moon: g= 8 x (0.71 m−0.47 m)
0.90 s ²−0.66 s ² = 8 x 0.24 m
0.3744 s ² =5.13 m/ s ²
Δg=g ( ΔH
H + 2T 1 ΔT 1
T 22−T 12 + 2T 2 ΔT 2
T 22−T 12 ) ……………………………. (2)
The theoretical or numerical value of gravitational acceleration is 9.80 m/s2 [4].
Procedure
The devices and materials used in this experiment included the following: a stopwatch, meter
stick, ball and marker. Two horizontal markers were drawn on the board then the distance
between them measured carefully and recorded as ΔH. One member of the group threw a ball up
vertically then the remaining members of the group recorded the time the ball crossed the first
and second horizontal markers.
Results
The measured and calculated results from the experiment are provided in Table 1 below.
Calculations of g:
The values of g are calculated using equation 1 as follows
Callisto moon: g= 8 x (0.81 m−0.61 m)
1.30 s ²−0.95 s ² = 8 x 0.2 m
0.7875 s ² =2.03 m/s ²
Larissa moon: g= 8 x (1 m−0.81 m)
1.30 s ²−1.12 s ² = 8 x 0.19 m
0.4356 s ² =3.49 m/ s ²
Earth: g= 8 x (1 m−0.71 m)
1.12 s ²−0.90 s ² = 8 x 0.29 m
0.4444 s ² =5.22m/ s ²
Io moon: g= 8 x (0.71 m−0.47 m)
0.90 s ²−0.66 s ² = 8 x 0.24 m
0.3744 s ² =5.13 m/ s ²
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Gravitational Acceleration – Group Report 4
Ceres moon: g= 8 x (1 m−0.61 m)
1.12 s ²−0.95 s ² = 8 x 0.39 m
0.3519 s ² =8.87 m/ s ²
Using Excel, the standard deviation of height and time is 0.18 and 0.22 respectively. The
standard error can be determined by dividing standard deviation by the square root of the number
of data points in the sample [5]. This is calculated as follows:
Standard error of time, ΔT = Standard deviationof time
√5 = 0.18
√5 =0.08
Standard error of height, ΔH = Standard deviation of height
√5 = 0.22
√5 =0.1
It is assumed that ΔT = ΔT1 = ΔT2 = 0.08
It is assumed that ΔH = ΔH1 = ΔH2 = 0.1
Calculations of Δg:
The values of are calculating using equation 2
Callisto moon: Δg=2.03 ( 0.1
0.2 + 2 x 0.95 x 0.08
1.3²−0.95² +2 x 1.3 x 0.08
1.3²−0.95² )=2.03 ( 0.5+ 0.19+0.26 ) =1.93
Larissa moon: Δg=3.49 ( 0.1
0.19 + 2 x 1.3 x 0.08
1.3²−1.12² +2 x 1.12 x 0.08
1.3²−1.12² )=3.49 ( 0.53+0.48+ 0.41 ) =4.96
Earth: Δg=5.22 ( 0.1
0.29 + 2 x 1.12 x 0.08
1.12²−0.9² + 2 x 0.9 x 0.08
1.12²−0.9² )=5.22 ( 0.34+0.40+ 0.32 ) =5.53
Io moon: Δg=5.13 ( 0.1
0.24 + 2 x 0.9 x 0.08
0.9²−0.66² + 2 x 0.66 x 0.08
0.9²−0.66² )=5.13 ( 0.42+0.39+0.28 )=5.59
Ceres moon: Δg=8.87 ( 0.1
0.39 + 2 x 0.95 x 0.08
1.12²−0.95² + 2 x 1.12 x 0.08
1.12²−0.95² )=8.87 ( 0.26+0.43+0.51 )=10.64
Ceres moon: g= 8 x (1 m−0.61 m)
1.12 s ²−0.95 s ² = 8 x 0.39 m
0.3519 s ² =8.87 m/ s ²
Using Excel, the standard deviation of height and time is 0.18 and 0.22 respectively. The
standard error can be determined by dividing standard deviation by the square root of the number
of data points in the sample [5]. This is calculated as follows:
Standard error of time, ΔT = Standard deviationof time
√5 = 0.18
√5 =0.08
Standard error of height, ΔH = Standard deviation of height
√5 = 0.22
√5 =0.1
It is assumed that ΔT = ΔT1 = ΔT2 = 0.08
It is assumed that ΔH = ΔH1 = ΔH2 = 0.1
Calculations of Δg:
The values of are calculating using equation 2
Callisto moon: Δg=2.03 ( 0.1
0.2 + 2 x 0.95 x 0.08
1.3²−0.95² +2 x 1.3 x 0.08
1.3²−0.95² )=2.03 ( 0.5+ 0.19+0.26 ) =1.93
Larissa moon: Δg=3.49 ( 0.1
0.19 + 2 x 1.3 x 0.08
1.3²−1.12² +2 x 1.12 x 0.08
1.3²−1.12² )=3.49 ( 0.53+0.48+ 0.41 ) =4.96
Earth: Δg=5.22 ( 0.1
0.29 + 2 x 1.12 x 0.08
1.12²−0.9² + 2 x 0.9 x 0.08
1.12²−0.9² )=5.22 ( 0.34+0.40+ 0.32 ) =5.53
Io moon: Δg=5.13 ( 0.1
0.24 + 2 x 0.9 x 0.08
0.9²−0.66² + 2 x 0.66 x 0.08
0.9²−0.66² )=5.13 ( 0.42+0.39+0.28 )=5.59
Ceres moon: Δg=8.87 ( 0.1
0.39 + 2 x 0.95 x 0.08
1.12²−0.95² + 2 x 1.12 x 0.08
1.12²−0.95² )=8.87 ( 0.26+0.43+0.51 )=10.64
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Gravitational Acceleration – Group Report 5
Table 1: Measured and calculated values
Moon/
planet
Height (m) Time (s) g (m/s2) Δg (m/s2) Experimental g (m/s2)
Callisto 0.61 0.95 2.03 1.93 3.96
Larissa 0.81 1.30 3.49 4.96 8.45
Earth 1 1.12 5.22 5.53 10.75
Io moon 0.71 0.90 5.13 5.59 10.72
Ceres 0.47 0.66 8.87 10.64 19.51
Average 0.72 0.986 4.948 5.73 10.68
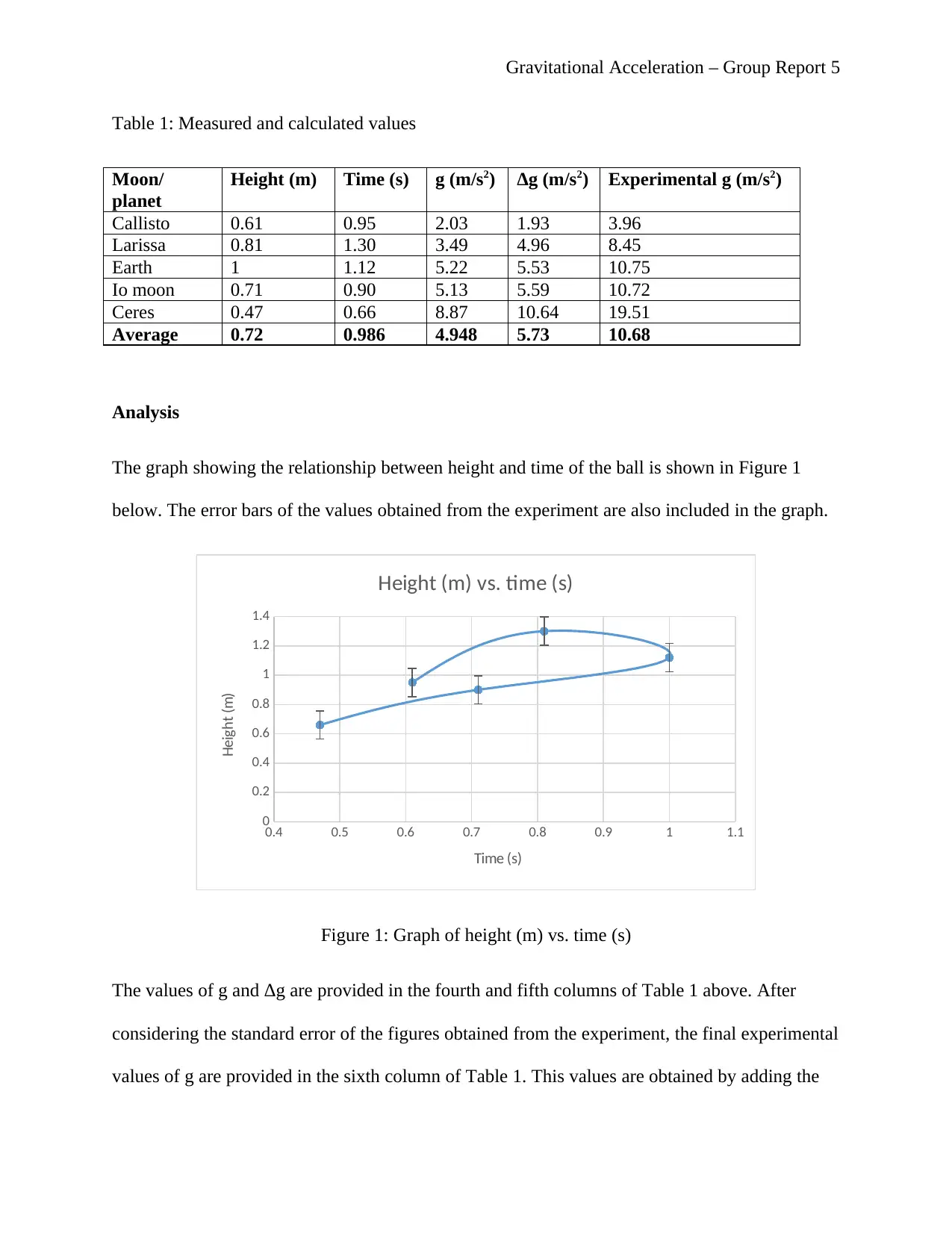
Analysis
The graph showing the relationship between height and time of the ball is shown in Figure 1
below. The error bars of the values obtained from the experiment are also included in the graph.
0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Height (m) vs. time (s)
Time (s)
Height (m)
Figure 1: Graph of height (m) vs. time (s)
The values of g and Δg are provided in the fourth and fifth columns of Table 1 above. After
considering the standard error of the figures obtained from the experiment, the final experimental
values of g are provided in the sixth column of Table 1. This values are obtained by adding the
Table 1: Measured and calculated values
Moon/
planet
Height (m) Time (s) g (m/s2) Δg (m/s2) Experimental g (m/s2)
Callisto 0.61 0.95 2.03 1.93 3.96
Larissa 0.81 1.30 3.49 4.96 8.45
Earth 1 1.12 5.22 5.53 10.75
Io moon 0.71 0.90 5.13 5.59 10.72
Ceres 0.47 0.66 8.87 10.64 19.51
Average 0.72 0.986 4.948 5.73 10.68
Analysis
The graph showing the relationship between height and time of the ball is shown in Figure 1
below. The error bars of the values obtained from the experiment are also included in the graph.
0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Height (m) vs. time (s)
Time (s)
Height (m)
Figure 1: Graph of height (m) vs. time (s)
The values of g and Δg are provided in the fourth and fifth columns of Table 1 above. After
considering the standard error of the figures obtained from the experiment, the final experimental
values of g are provided in the sixth column of Table 1. This values are obtained by adding the

Gravitational Acceleration – Group Report 6
values in the fourth and fifth columns. It is important to note that Δg can either be positive or
negative. In this case, positive values were used because the gravitation acceleration was
assumed to be positive – the free ball was accelerating along its trajectory. Therefore the average
g is 10.68 m/s2.
Conclusion
The gravitation acceleration in Melbourne is 9.7997 m/s2 ≈ 9.8 m/s2. The percentage difference
between the experimental g and g in Melbourne is calculated as follows:
% difference= Experimental value−Theoretical value
Experimental value x 100 %
= 10.68−9.8
10.68 x 100 %=8.2 %
Since the percentage difference between the value of gravitational acceleration obtained from the
experiment and the numerical value in Melbourne is 8.2%, which is relatively small, the
experiment can be said to have been performed to the expected accuracy level.
However, the accuracy of this experiment can be improved in the future through the following
means: ensuring that the devices (meter stick and stopwatch) used do not have any defects;
avoiding parallax error by ensuring that the meter stick is positioned vertically and the
measurements of height of the free ball read horizontal to the marked points on the meter stick;
improving reaction time of participants by ensuring that they read and record the exact time that
the ball passes through the specified points; by performing the experiment in a room where flow
of air is controlled (enclosed room where there is minimal entry and exit of air); ensuring that the
stopwatch is calibrated appropriately before starting to take time measurements; ensuring that the
values in the fourth and fifth columns. It is important to note that Δg can either be positive or
negative. In this case, positive values were used because the gravitation acceleration was
assumed to be positive – the free ball was accelerating along its trajectory. Therefore the average
g is 10.68 m/s2.
Conclusion
The gravitation acceleration in Melbourne is 9.7997 m/s2 ≈ 9.8 m/s2. The percentage difference
between the experimental g and g in Melbourne is calculated as follows:
% difference= Experimental value−Theoretical value
Experimental value x 100 %
= 10.68−9.8
10.68 x 100 %=8.2 %
Since the percentage difference between the value of gravitational acceleration obtained from the
experiment and the numerical value in Melbourne is 8.2%, which is relatively small, the
experiment can be said to have been performed to the expected accuracy level.
However, the accuracy of this experiment can be improved in the future through the following
means: ensuring that the devices (meter stick and stopwatch) used do not have any defects;
avoiding parallax error by ensuring that the meter stick is positioned vertically and the
measurements of height of the free ball read horizontal to the marked points on the meter stick;
improving reaction time of participants by ensuring that they read and record the exact time that
the ball passes through the specified points; by performing the experiment in a room where flow
of air is controlled (enclosed room where there is minimal entry and exit of air); ensuring that the
stopwatch is calibrated appropriately before starting to take time measurements; ensuring that the
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Gravitational Acceleration – Group Report 7
same force is used every time the ball is thrown up; and taking several values for each time and
height measurements and then determining the average value.
References
[1] The Physics Classroom, "Kinematics equations and free fall," (n.d.). [Online]. Available:
https://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations-and-Free-Fall.
[Accessed 6 April 2019].
[2] D. MacDougal, Newton's Gravity: An Introductory Guide to the Mechanics of the Universe, New
York: Springer-Verlag, 2012.
[3] P. Johnson and R. Coleman, "Experiment: Measuring the acceleration of gravity: ag," 15 June 2015.
[Online]. Available: https://mypages.iit.edu/~smart/martcar/lesson2/free-fall-experiment.html.
[Accessed 6 April 2019].
[4] N. Suwanpayak, S. Sutthiyan, K. Kulsirirat, P. Srisongkram, C. Teeka and P. Buranasiri, "A comparison
of gravitational acceleration measurement methods for undergraduate experiment," Journal of
Physics Conference Series, vol. 1144, no. 1, pp. 1-6, 2018.
[5] L. Johnson, "How to Calculate Error Bars," 31 March 2015. [Online]. Available:
https://www.techwalla.com/articles/how-to-calculate-error-bars. [Accessed 6 April 2019].
same force is used every time the ball is thrown up; and taking several values for each time and
height measurements and then determining the average value.
References
[1] The Physics Classroom, "Kinematics equations and free fall," (n.d.). [Online]. Available:
https://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations-and-Free-Fall.
[Accessed 6 April 2019].
[2] D. MacDougal, Newton's Gravity: An Introductory Guide to the Mechanics of the Universe, New
York: Springer-Verlag, 2012.
[3] P. Johnson and R. Coleman, "Experiment: Measuring the acceleration of gravity: ag," 15 June 2015.
[Online]. Available: https://mypages.iit.edu/~smart/martcar/lesson2/free-fall-experiment.html.
[Accessed 6 April 2019].
[4] N. Suwanpayak, S. Sutthiyan, K. Kulsirirat, P. Srisongkram, C. Teeka and P. Buranasiri, "A comparison
of gravitational acceleration measurement methods for undergraduate experiment," Journal of
Physics Conference Series, vol. 1144, no. 1, pp. 1-6, 2018.
[5] L. Johnson, "How to Calculate Error Bars," 31 March 2015. [Online]. Available:
https://www.techwalla.com/articles/how-to-calculate-error-bars. [Accessed 6 April 2019].
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




