HA1011 Statistics Assignment: Data Analysis, Probability, Holmes

This assignment solution for HA1011 Statistics covers various statistical concepts, including data analysis, probability, and regression. It begins with constructing a frequency distribution and histogram from passenger data at Melbourne train stations, followed by calculating mean, median, and mode. The assignment then explores the relationship between student attendance and chocolate bar sales using standard deviation, interquartile range (IQR), and correlation coefficient. Furthermore, it involves calculating and interpreting a regression equation to predict chocolate bar sales based on student attendance, along with the coefficient of determination. The assignment also delves into probability calculations related to player recruitment and training in a cricket team, using Bayes' Rule to analyze market research data for launching new products. The solutions provide detailed workings and interpretations, demonstrating a comprehensive understanding of statistical principles and their practical applications.

HOLMES INSTITUTE
FACULTY OF HIGHER EDUCATION
HA1011 Group Assignment
Due End of Week 10
WORTH 20%
(Maximum 5 students in the group)
1

Attempt all the questions (8x2.5 = 20 Marks)
Question 1 of 8
HINT: We cover this in Lecture 1 (Summary Statistics and Graphs)
Data were collected on the number of passengers at each train station in Melbourne. The
numbers for the weekday peak time, 7am to 9:29am, are given below.
456 1189 410 318 648 399 382 248 379 1240 2268 272
267 1113 733 262 682 906 338 1750 530 1584 2985 323
1311 1632 1606 982 878 169 583 548 429 658 344 2630
538 494 1946 268 435 862 866 579 1359 1022 1618 1021
401 1181 1178 637 2830 1000 2958 962 697 401 1442 1115
Tasks:
a. Construct a frequency distribution using 10 classes, stating the Frequency, Relative
Frequency, Cumulative Relative Frequency and Class Midpoint
Answer
Class
Interval
Mid-point Frequency Relative
Frequency
Cumulative Relative
Frequency
100-400 250 13 21.67% 21.67%
401-700 550 17 28.33% 50.00%
701-1000 850 8 13.33% 63.33%
1001-1300 1150 8 13.33% 76.67%
1301-1600 1450 4 6.67% 83.33%
1601-1900 1750 4 6.67% 90.00%
1901-2100 2050 1 1.67% 91.67%
2101-2400 2350 1 1.67% 93.33%
2401-2700 2650 1 1.67% 95.00%
2701-3000 2950 3 5.00% 100.00%
b. Using (a), construct a histogram. (You can draw it neatly by hand or use Excel)
Answer
2

c. Based upon the raw data (NOT the Frequency Distribution), what is the mean, median
and mode? (Hint – first sort your data. This is usually much easier using Excel.)
Answer
Number of passengers
Mean 954.37
Median 715
Mode 401
Question 2 of 8
HINT: We cover this in Lecture 2 (Measures of Variability and Association)
You are the manager of the supermarket on the ground floor below Holmes. You are
wondering if there is a relation between the number of students attending class at Holmes
each day, and the amount of chocolate bars sold. That is, do you sell more chocolate bars
when there are a lot of Holmes students around, and less when Holmes is quiet? If there is a
relationship, you might want to keep less chocolate bars in stock when Holmes is closed over
the upcoming holiday. With the help of the campus manager, you have compiled the
following list covering 7 weeks:
3

Weekly attendance Number of chocolate bars sold
472 6916
413 5884
503 7223
612 8158
399 6014
538 7209
455 6214
Tasks:
a. Is above a population or a sample? Explain the difference.
Answer
This is a sample. This is because the data is just for a selected number of weeks.
Population would have required considering all the dataset since Holmes probably
started.
b. Calculate the standard deviation of the weekly attendance. Show your workings. (Hint
– remember to use the correct formula based upon your answer in (a).)
Answer
x= 472+ 413+503+612+399+538+455
7 =3392
7 =484.5714
SD= √ ∑
i=1
n
( xi −x )2
n−1 = √ ( 472−484.57 )2 + ( 413−484.57 )2 +…+ ( 538−484.57 )2+ ( 455−484.57 )2
30−1 = √ 32909.71
7−1 =
c. Calculate the Inter Quartile Range (IQR) of the chocolate bars sold. When is the IQR
more useful than the standard deviation? (Give an example based upon number of
chocolate bars sold.)
Answer
IQR=Q3 −Q1
Q3=7216
4

Q1=6114
IQR=Q3 −Q1 → 7216−6114=1102
IQR is more useful in cases where there are outliers and the data seems not to be
normally distributed.
Example is when we for instance have chocolate bars sold more than 8869 or less
than 5563.
d. Calculate the correlation coefficient. Using the problem we started with, interpret the
correlation coefficient. (Hint – you are the supermarket manager. What does the
correlation coefficient tell you? What would you do based upon this information?)
Answer
r = n ∑ xy −∑ x ∑ y
√ [ n∑ x2− ( ∑ x )
2
] [ n∑ y2− ( ∑ y ) 2
]
∑ xy =23425707
∑ x =3392
∑ y=47618
∑ x2=1676576
∑ y2 =327928878
r = n ∑ xy −∑ x ∑ y
√ [ n∑ x2− (∑ x )2
] [ n∑ y2− (∑ y )2
] = 7∗23425707−3392∗47618
√ ( 7∗1676576−33922 ) ( 7∗327928878−476182 ) =0.96799
The correlation coefficient is 0.96799. This shows that there is a very strong relationship
between student’s weekly attendance and the number of chocolate bars sold. That is, an
increase in the number of weekly attendance is expected to increase the number of chocolate
bars sold. Based on this information I would stock more chocolate bars when there are a lot
of Holmes students around, and less when Holmes is quiet. I would be prompted to keep less
chocolate bars in stock when Holmes is closed over the upcoming holiday.
5

Question 3 of 8
HINT: We cover this in Lecture 3 (Linear Regression)
(We are using the same data set we used in Question 2)
You are the manager of the supermarket on the ground floor below Holmes. You are
wondering if there is a relation between the number of students attending class at Holmes
each day, and the amount of chocolate bars sold. That is, do you sell more chocolate bars
when there are a lot of Holmes students around, and less when Holmes is quiet? If there is a
relationship, you might want to keep less chocolate bars in stock when Holmes is closed over
the upcoming holiday. With the help of the campus manager, you have compiled the
following list covering 7 weeks:
Weekly attendance Number of chocolate bars sold
472 6916
413 5884
503 7223
612 8158
399 6014
538 7209
455 6214
Tasks:
a. Calculate AND interpret the Regression Equation. You are welcome to use Excel to
check your calculations, but you must first do them by hand. Show your workings.
(Hint 1 - As manager, which variable do you think is the one that affects the other
variable? In other words, which one is independent, and which variable’s value is
dependent on the other variable? The independent variable is always x.
Hint 2 – When you interpret the equation, give specific examples. What happens
when Holmes are closed? What happens when 10 extra students show up?)
Answer
6

In this problem, the independent variable (x) is the weekly attendance while
dependent variable (y) is the number of chocolate bars sold. This is because the
weekly attendance is believed to affect the number of chocolate bars sold.
We compute the regression parameters as follows;
a= (∑ y ) (∑ x2 )− (∑ x ) (∑ xy )
n ( ∑ x2 )− (∑ x )2
b= n ( ∑ xy )− (∑ x ) (∑ y )
n (∑ x2 )− (∑ x )2
∑ xy =23425707
∑ x =3392
∑ y=47618
∑ x2=1676576
a= ( ∑ y ) ( ∑ x2 ) − ( ∑ x ) ( ∑ xy )
n ( ∑ x2 )− ( ∑ x )
2 = 47618∗1676576−3392∗23425707
7∗1676576−33922 =1628.689
b= n ( ∑ xy ) − ( ∑ x ) ( ∑ y )
n ( ∑ x2 ) − ( ∑ x )
2 =7∗23425707−3392∗47618
7∗1676576−33922 =10.67723
From the calculations the regression equation is given as follows;
Number of chocolate bars sold=1628.689+10.67723(weekly attendance)
From the regression equation we can make the following interpretations;
The coefficient of weekly attendance is 10.67723; this means that a unit increase in
the weekly attendance would result to an increase in the number of chocolate sold by
approximately 11. Also if 10 extra students show up we would expect the number of
chocolate bars sold to increase by approximately 107.
7

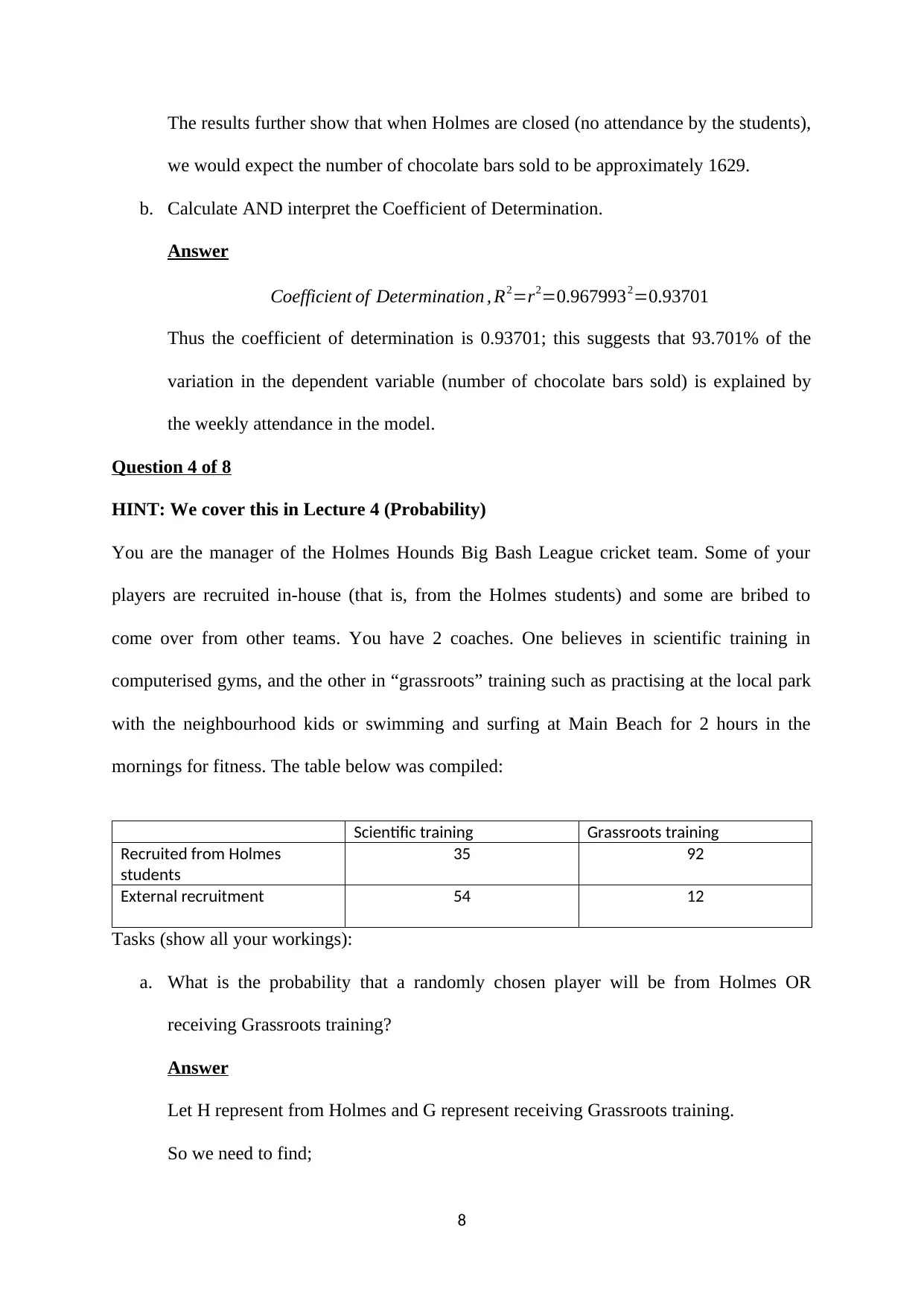
The results further show that when Holmes are closed (no attendance by the students),
we would expect the number of chocolate bars sold to be approximately 1629.
b. Calculate AND interpret the Coefficient of Determination.
Answer
Coefficient of Determination , R2=r2=0.9679932=0.93701
Thus the coefficient of determination is 0.93701; this suggests that 93.701% of the
variation in the dependent variable (number of chocolate bars sold) is explained by
the weekly attendance in the model.
Question 4 of 8
HINT: We cover this in Lecture 4 (Probability)
You are the manager of the Holmes Hounds Big Bash League cricket team. Some of your
players are recruited in-house (that is, from the Holmes students) and some are bribed to
come over from other teams. You have 2 coaches. One believes in scientific training in
computerised gyms, and the other in “grassroots” training such as practising at the local park
with the neighbourhood kids or swimming and surfing at Main Beach for 2 hours in the
mornings for fitness. The table below was compiled:
Scientific training Grassroots training
Recruited from Holmes
students
35 92
External recruitment 54 12
Tasks (show all your workings):
a. What is the probability that a randomly chosen player will be from Holmes OR
receiving Grassroots training?
Answer
Let H represent from Holmes and G represent receiving Grassroots training.
So we need to find;
8

P ( H∨G ) =P ( H ) + P ( G ) −P( H ∧G)
P ( H )= 127
193 =0.65803
P ( G )= 104
193 =0.53886
P ( H∧G )= 92
193 =0.47668
P ( H∨G )=0.65803+0.53886−0.47668=0.72021
Thus probability is 0.72021 or 72.021%
b. What is the probability that a randomly selected player will be External AND be in
scientific training?
Answer
P ( E∧S )= 54
193 =0.27979
c. Given that a player is from Holmes, what is the probability that he is in scientific
training?
Answer
P ( S∨H ) = P ( S∧H )
P(H )
P ( S∧H ) = 35
193 =0.181347
P ( H )= 127
193 =0.65803
P ( S∨H ) = P ( S∧H )
P( H ) = 0.181347
0.65803 =0.27559
d. Is training independent from recruitment? Show your calculations and then explain in
your own words what it means.
Answer
For independence we have;
9

P ( S∧H ) =P ( S ) × P(H )
P ( S ) = 89
193
P ( H ) = 127
193
P ( S ) × P ( H ) =
89
193∗127
193 =0.30344
P ( S∧H ) = 35
193 =0.181347
From the above, we can see that
P ( S∧H ) ≠ P ( S ) × P( H )
Thus we can conclude that training is not independent from recruitment. This means
that the kind of training one gets depends on how the person was recruited.
Question 5 of 8
HINT: We cover this in Lecture 5 (Bayes’ Rule)
A company is considering launching one of 3 new products: product X, Product Y or Product
Z, for its existing market. Prior market research suggest that this market is made up of 4
consumer segments: segment A, representing 55% of consumers, is primarily interested in the
functionality of products; segment B, representing 30% of consumers, is extremely price
sensitive; and segment C representing 10% of consumers is primarily interested in the
appearance and style of products. The final 5% of the customers (segment D) are fashion
conscious and only buy products endorsed by celebrities.
To be more certain about which product to launch and how it will be received by each
segment, market research is conducted. It reveals the following new information.
 The probability that a person from segment A prefers Product X is 20%
 The probability that a person from segment B prefers product X is 35%
 The probability that a person from segment C prefers Product X is 60%
10

 The probability that a person from segment C prefers Product X is 90%
Tasks (show your workings):
A. The company would like to know the probably that a consumer comes from segment
A if it is known that this consumer prefers Product X over Product Y and Product Z.
Answer
P ( A |X ) = P ( A∧X )
P ( X )
P ( A∧ X ) =0.55∗0.2=0.11
P ( X )=P ( A∧X ) + ( B∧ X )+P ( C∧ X )+ P ( D∧X )
¿ 0.5 5∗0.2+ 0.30∗0.35+0.10∗0.60+0.05∗0.90=0.11+ 0.105+0.06+0.045
¿ 0.32
P ( A |X ) = P ( A∧X )
P ( X ) = 0.11
0.32 =0.34375
11
A
B
C
D
0.55
0.30
0.10
0.05
Prefers X
Does not Prefer X
Prefers X
Does not Prefer X
Prefers X
Does not Prefer X
Prefers X
Does not Prefer X
0.20
0.80
0.35
0.65
0.60
0.40
0.90
0.10

Thus the probability that a consumer comes from segment A if it is known that this
consumer prefers Product X over Product Y and Product Z is 0.34375.
B. Overall, what is the probability that a random consumer’s first preference is product
X?
Answer
P ( X ) =P ( A∧X ) + ( B∧ X ) + P ( C∧ X ) + P ( D∧X )
¿ 0.55∗0.2+0.30∗0.35+0.10∗0.60+0.05∗0.90=0.11+ 0.105+0.06+0.045
¿ 0.32
Thus the probability that a random consumer’s first preference is product X is 0.32.
Question 6 of 8
HINT: We cover this in Lecture 6
You manage a luxury department store in a busy shopping centre. You have extremely high
foot traffic (people coming through your doors), but you are worried about the low rate of
conversion into sales. That is, most people only seem to look, and few actually buy anything.
You determine that only 1 in 10 customers make a purchase. (Hint: The probability that the
customer will buy is 1/10.)
Tasks (show your workings):
A. During a 1 minute period you counted 8 people entering the store. What is the
probability that only 2 or less of those 8 people will buy anything? (Hint: You have to
do this by hand, showing your workings. Use the formula on slide 11 of lecture 6. But
you can always check your calculations with Excel to make sure they are correct.)
Answer
P(2∨less)=P(2)+ P (1)+P( 0)
P ( 2 )=C2
8∗0.12∗0.96= 8 !
6 ! 2 !∗0.12∗0.96=0.148803
12

P ( 1 ) =C1
8∗0.11∗0.97= 8 !
7 ! 1! ∗0.11∗0.97 =0.382638
P ( 0 )=C0
8∗0.10∗0.98= 8 !
8! 0!∗0.10∗0.98=0.430467
P ( 2∨less ) =P ( 2 ) + P ( 1 ) + P ( 0 )=0.148803+0.382638+0.430467=0.961908
P ( 2∨less ) =0.961908
B. (Task A is worth the full 2 marks. But you can earn a bonus point for doing Task B.)
On average you have 4 people entering your store every minute during the quiet 10-
11am slot. You need at least 6 staff members to help that many customers but usually
have 7 staff on roster during that time slot. The 7th staff member rang to let you know
he will be 2 minutes late. What is the probability 9 people will enter the store in the
next 2 minutes? (Hint 1: It is a Poisson distribution. Hint 2: What is the average
number of customers entering every 2 minutes? Remember to show all your
workings.)
Answer
The average number of customersentering per minute=4
The average number of customersentering every 2 minutes=2∗4=8
P ( X )= e− μ μx
x !
P ( X=9 )= e−8 89
9 ! =0.124077
Thus the probability 9 people will enter the store in the next 2 minutes is 0.124077.
Question 7 of 8
HINT: We cover this in Lecture 7
13

You are an investment manager for a hedge fund. There are currently a lot of rumours going
around about the “hot” property market on the Gold Coast, and some of your investors want
you to set up a fund specialising in Surfers Paradise apartments.
You do some research and discover that the average Surfers Paradise apartment currently
sells for $1.1 million. But there are huge price differences between newer apartments and the
older ones left over from the 1980’s boom. This means prices can vary a lot from apartment
to apartment. Based on sales over the last 12 months, you calculate the standard deviation to
be $385 000.
There is an apartment up for auction this Saturday, and you decide to attend the auction.
Tasks (show your workings):
A. Assuming a normal distribution, what is the probability that apartment will sell for
over $2 million?
Answer
We seek to find;
P(X > 2000000)
So we calculate the Z-score as follows;
Z= X−μ
σ = 2000000−1100000
385000 =2.337662
P ( Z >2.337662 )=1−0. 009704=0.990296
Thus the probability that apartment will sell for over $2 million is 0.09704
B. What is the probability that the apartment will sell for over $1 million but less than
$1.1 million?
Answer
We seek to find;
P(1000000<X <1100000)
So we calculate the z score as follows;
14

Z= X−μ
σ = 1 000000−1100000
385000 =−0.25974
Z= X−μ
σ = 11 00000−1100000
385000 =0
P( Z>−0.25974)=1−0.397432=0.602468
P( Z<0.00000)=0.5
P (−0.25974< XZ<0 )=0.6024 68−0.5=0.102468
Thus the probability that the apartment will sell for over $1 million but less than $1.1
million is 0.102468.
Question 8 of 8
HINT: We cover this in Lecture 8
You are an investment manager for a hedge fund. There are currently a lot of rumours going
around about the “hot” property market on the Gold Coast, and some of your investors want
you to set up a fund specialising in Surfers Paradise apartments.
Last Saturday you attended an auction to get “a feel” for the local real estate market. You
decide it might be worth further investigating. You ask one of your interns to take a quick
sample of 50 properties that have been sold during the last few months. Your previous
research indicated an average price of $1.1 million but the average price of your assistant’s
sample was only $950 000.
However, the standard deviation for her research was the same as yours at $385 000.
Tasks (show your workings):
A. Since the apartments on Surfers Paradise are a mix of cheap older and more expensive
new apartments, you know the distribution is NOT normal. Can you still use a Z-
distribution to test your assistant’s research findings against yours? Why, or why not?
Answer
15

Yes you can still use z-distribution to test the claim. This is because the sample size is
large enough (n > 30). The larger the sample size, the more the data is close to normal
distribution.
B. You have over 2 000 investors in your fund. You and your assistant phone 45 of them
to ask if they are willing to invest more than $1 million (each) to the proposed new
fund. Only 11 say that they would, but you need at least 30% of your investors to
participate to make the fund profitable. Based on your sample of 45 investors, what is
the probability that 30% of the investors would be willing to commit $1 million or
more to the fund?
Answer
^p= x
n = 11
45
p= 30
100 = 3
10
Z= ^p− p
√ p ( 1−p )
n
=
11
45 −0.3
√ 0.3 ( 1−0.3 )
45
=−0.81325
P( Z=−0.81325)=0.416218
Thus the probability that 30% of the investors would be willing to commit $1 million
or more to the fund is 0.416218.
16