HIT400 Discrete Structures Assignment 1: Graph Theory and Functions

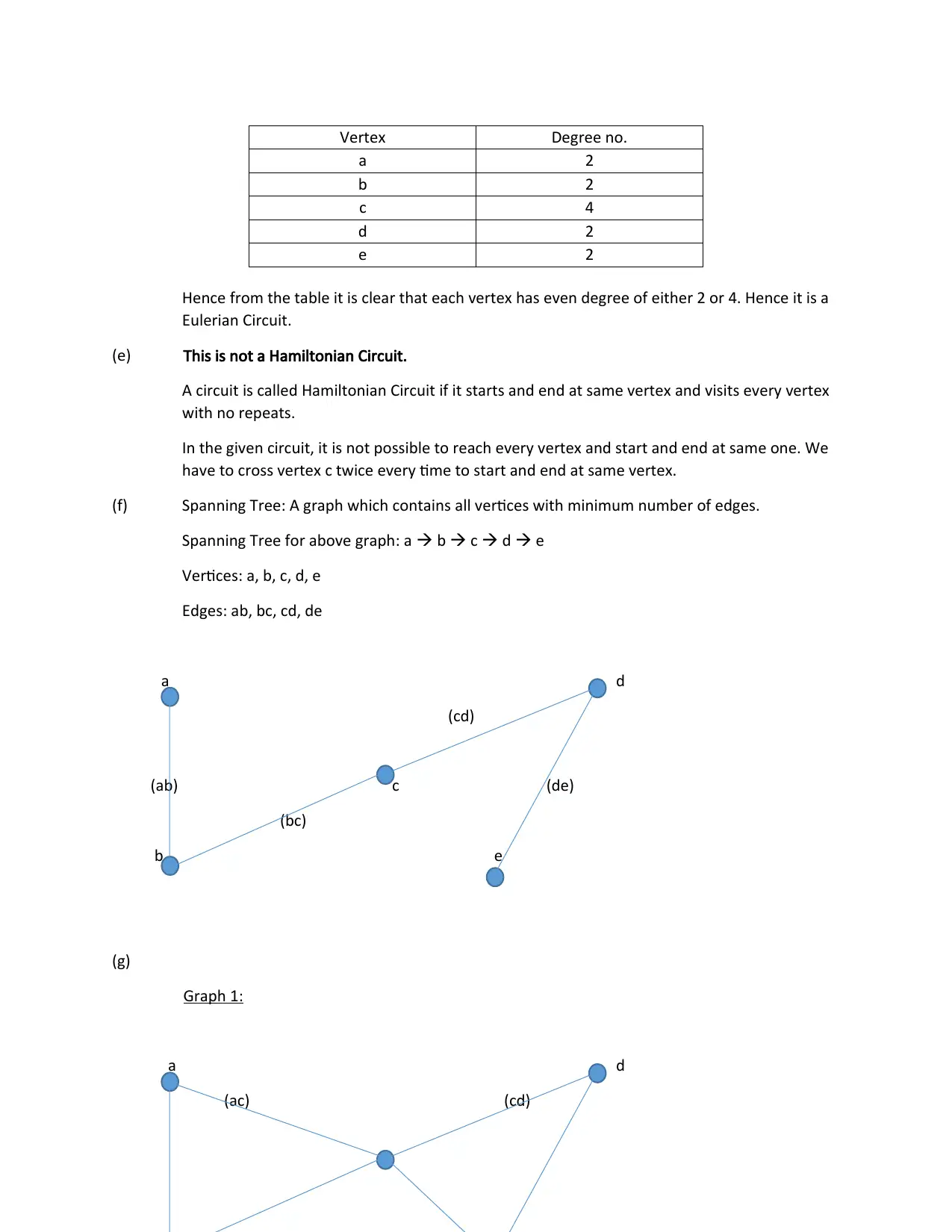
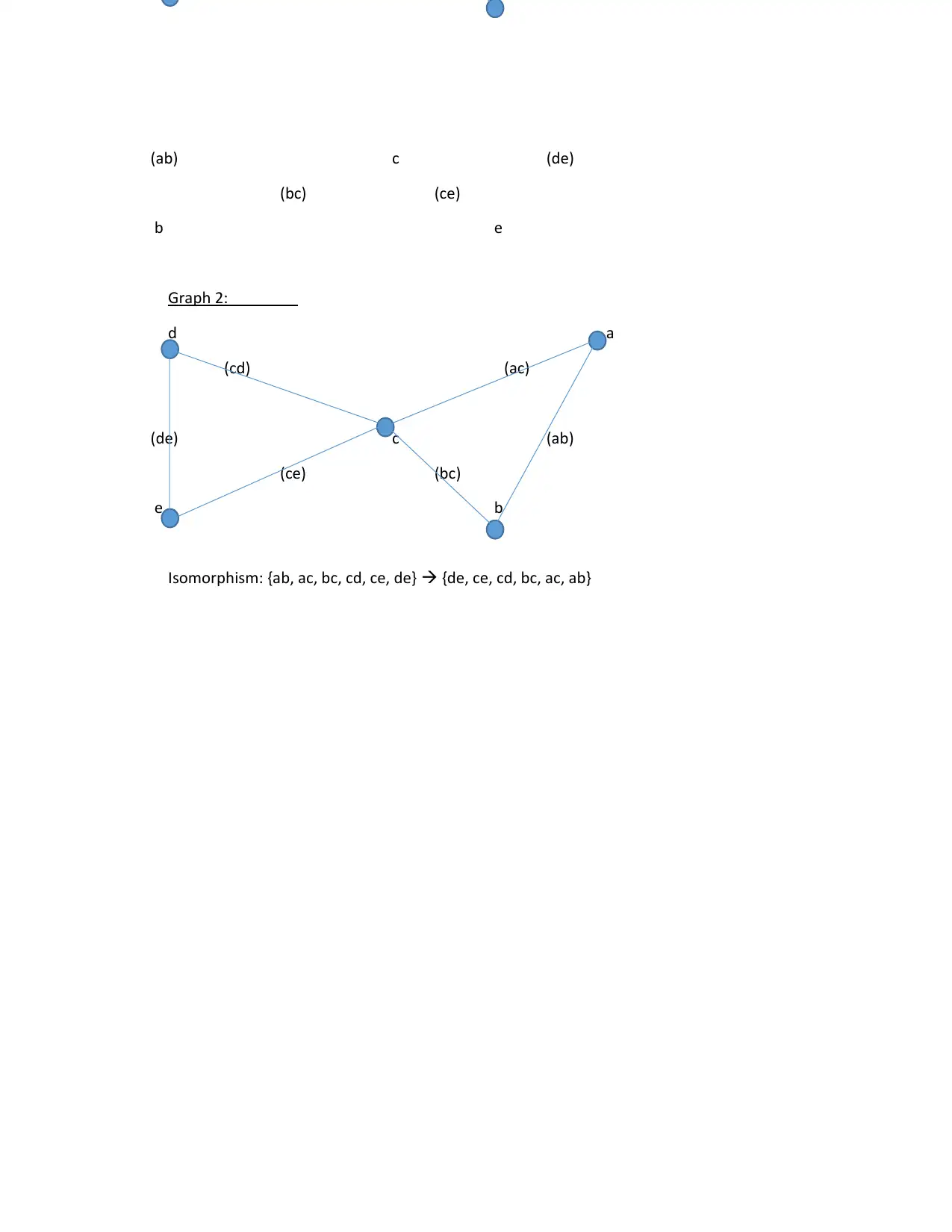
This assignment solution addresses three problems related to discrete structures. The first problem explores functions and their compositions, including the analysis of a function f: R → [0,1] and g: [0,1] → [-1,1], and the evaluation of (g o f)(x) and (f o g)(x). The second problem involves mathematical induction, specifically proving or disproving the inequality ∑(2i-1)/i^4 ≤ 4 - (2n+1)/n^2. The third problem delves into graph theory, examining a given graph's properties. The analysis includes determining if the graph is complete, regular, connected, Eulerian, or Hamiltonian, and identifying a spanning tree and demonstrating graph isomorphism between two graphs. The solution provides detailed explanations and justifications for each part of the problems.

1.f : R [0,1]g : [0,1]  [-1,1]g(x) = 2y-1(gof)(x) = 2(f(x)) – 1
= {2|x|−1−1 |x|>1
2|x|−1 |x|<1
(Fog)(x) = {|2 y−1|−1 |2 y−1|>1
|2 y−1||2 y−1|<1
Case 1:
|2 y−1|>1
2y -1 >1 or -(2y - 1) >1
2y >2 or -2y>0
y>1 or y<0
y == {-∞, 0} U {1, ∞}
Case 2:
|2y - 1|<1
2y-1 < 1 or -(2y-1) < 1
2y<2 or -2y<0
y<1 or y>0
y == {0,1}
(Fog)(x) = {|2 y−1|−1 y ∈ {−∞ , 0 }∪{1 , ∞ }
|2 y−1| y ∈{0,1}
2.
∑
i=1
n (2i2−1)
i4 < 4−2 n+1
n2
At n=1,

∑
i=1
1 (2i2−1)
i4 =1≤ 4− 2 ( 1 )+1
12 ≤ 4−3 ≤1 ……….{Correct Result}
At any positive integer value n = k+1,
∑
i=1
k (2i2−1)
i4 + 2 ( k +1 )2−1
¿ ¿
≤ 4− ( 2 k +1 ) ( k +1 )4−2k 2 ( k +1 )2 + k2
k2 ( k +1 )4
≤ 4− ( k +1 ) 2 ( ( 2 k +1 ) ( k2 +2 k +1 )−2k 2 ) +k 2
k2 ( k +1 ) 4
≤ 4− ( k +1 ) 2 ( 2 k3+ 4 k2+ 2 k+ k2 +2 k +1−2 k2 ) + k2
k2 ( k +1 ) 4
≤ 4− ( k +1 ) 2 ( 2 k3+ 2 k2+ 4 k+ k2 +1 ) +k 2
k 2 ( k +1 ) 4
≤ 4− 4 k2+ 4 k+ 1−2 k2
k2 ( k +1 ) 2
≤ 4− 2 k2+ 4 k+ 1
k 2 ( k +1 ) 2
≤ 4−2 (k ¿¿ 2+2 k +1)−2+1
k2 ( k +1 )2 ¿
≤ 4− 2 ( k +1 )2−1
k2 ( k +1 )2
Therefore, sum (-1 + 2 i^2)/i^4<=4 - (2 n + 1)/n^2 is not always true for
i>0 and i element Z
3.
V = {a, b, c, d, e}
E = {ab, ac, bc, cd, ce, de}
a d

(ac) (cd)
(ab) c (de)
(bc) (ce)
b e
(a) This is not a complete graph.
A complete graph has its every vertex connected to each other with a direct link.
Let number of vertices be n then number of edges is given by formula,
No. of edges = n(n+1)/2
Here, n= 5,
E = 5*6/2 = 15
But E given in question is 6.
Hence it is not a complete graph.
(b) This is not a regular graph.
For a graph to be regular every vertex in it should have equal number of neighboring vertexes.
From above table we can see that c has 4 neighbor vertexes with others have only 2.
(c) This is connected graph.
For a graph to be called as ‘connected graph’, there must be at least one path from any vertex
to any other vertex.
In the above graph, we can observe that each point is connected to every other point with at
least one direct or indirect path.
(d) This is a Eulerian Circuit.
For any graph to be Eulerian circuit, every vertex present should have even degrees. Number
of degree is total number of paths from a given vertex.
Vertex No. of neighbor vertexes
a 2
b 2
c 4
d 2
e 2

Hence from the table it is clear that each vertex has even degree of either 2 or 4. Hence it is a
Eulerian Circuit.
(e) This is not a Hamiltonian Circuit.
A circuit is called Hamiltonian Circuit if it starts and end at same vertex and visits every vertex
with no repeats.
In the given circuit, it is not possible to reach every vertex and start and end at same one. We
have to cross vertex c twice every time to start and end at same vertex.
(f) Spanning Tree: A graph which contains all vertices with minimum number of edges.
Spanning Tree for above graph: a  b  c  d  e
Vertices: a, b, c, d, e
Edges: ab, bc, cd, de
a d
(cd)
(ab) c (de)
(bc)
b e
(g)
Graph 1:
a d
(ac) (cd)
Vertex Degree no.
a 2
b 2
c 4
d 2
e 2

(ab) c (de)
(bc) (ce)
b e
Graph 2:
d a
(cd) (ac)
(de) c (ab)
(ce) (bc)
e b
Isomorphism: {ab, ac, bc, cd, ce, de}  {de, ce, cd, bc, ac, ab}