Biomechanical Modeling of Human Gait: Advancements and Analysis

This report provides a comprehensive overview of biomechanical modeling of human gait, focusing on model-based approaches. It begins with an introduction to human gait, its definition, and the importance of gait analysis, including its applications in sports biomechanics and the assessment of individuals with walking impairments. The report then delves into a literature review of three key research papers. The first paper explores automated person recognition through walking and running gaits, introducing coupled oscillator models to reduce data collection. The second paper examines bipedal human walking control derived from the analysis of robotic locomotion, proposing a controller design that utilizes the relationship between sensory input and motor output. The third paper presents a theoretical and computational model of human gait to simulate pathological patterns, utilizing a biped model based on an inverted pendulum to describe both normal and pathological movements. Each research paper's model, including the Van der Pol oscillator, least mean squares method, and inverted pendulum model, is discussed in detail, offering insights into the methodologies and findings. The report highlights the advancements and applications of biomechanical modeling in understanding and analyzing human locomotion.

Running Head: BIOMECHANICAL MODELING OF HUMAN GAIT
1
BIOMECHANICAL MODELING OF HUMAN GAIT
Student Name
Institution Affiliation
Facilitator
Course
Date

BIOMECHANICAL MODELING OF HUMAN GAIT 2
Introduction
In its basic definition, Human gait is the locomotion achieved as human beings move
their limbs. It’s commonly defined as the bipedal and biphasic forward impulsion of the human
body’s center of gravity besides the sinuous movements of other body segments under minimal
use of energy. Gait patterns are described by the different patterns of limb-movement, the overall
velocity, kinetic and potential energy cycles. Human gaits are therefore the different ways
through which the human bodies move naturally or through a specialized training (Dupuis,
Savatier & Vasseur, 2013). On the other hand, Gait analysis entails the systematic examination
of human locomotion as well as other animals through eye observations by third parties
augmented by instrumentation for computing body movements, mechanics and muscle activities.
Mainly, Gait analysis techniques are utilized used to assess and treat individuals with conditions
affecting their ability to walk. It is also commonly used in sports biomechanics to enhance the
efficiency of athletes in running and to identify movement and posture related problems in
people with injuries (Nandy & Chakraborty, 2017).
Human gait is achieved through the coordination of neuromuscular and
musculotendinous elements of a body in motion working together to come up with body
dynamics. The synchronization of those different body parts has been scrutinized by different
researchers to understand motion dynamics. A sample human gait has been presented as in the
figure below to help in understanding how the human gait dynamics change when a person is in
motion (Lishani, Boubchir, Khalifa & Bouridane, 2017).

BIOMECHANICAL MODELING OF HUMAN GAIT 3
Mainly, human gait analysis has been divided into two main approaches. The two
approaches are model-free approaches and model-based approaches. With the model-free
approach, motion information of a body in motion is used directly as it’s obtained from
silhouettes while model-based approaches map models to represent the human body gait using
the parameters of models that update dynamically (Hu, Wang, Zhang, Zhang & Little, 2013).
Compared to, model-based approach, model-free approaches has recently captured the attention
of most of the researchers and has begun to shift from model-based approaches to this approach
because of its performance, robustness and low computational performance as compared to
model-based approach. This paper reviews the current advancements in the model-based
approaches.
Literature Review
Research 1: Automated person recognition by walking and running via model-based
approaches

BIOMECHANICAL MODELING OF HUMAN GAIT 4
In this research, the authors observed that gait analysis enjoys more benefits than other
biometric studies because it is difficult for it to be disguised and can also be perceived from a
distance. According to them, most of the gait analysis approaches applied currently concentrate
on walking only and are mainly statistical. This study, therefore, concentrated on analyzing the
motion of the leg in order to show that people can be recognized not only through walking gait
but also through their running gait (Yam, Nixon & Carter 2004). They came up with two new
modeling techniques which employed a coupled oscillator and human locomotive biomechanics
as the underlying concept. According to the three authors, the two models would provide
plausible methods to reduce the amount of data collected because they would provide inclination
estimates of thighs and that of legs from the image data. The two models would also derive some
phase-weighted Fourier descriptions of gait signatures using an automated non-invasive way.
Although the two models would operate in a similar manner, the difference between them is that
one of them required a specification of all the parameters to differentiate walking and running
while the other one would be completely automated. Eventually, the two models proved that both
gaits were potential biometrics but running being more potent. The model proved to withstand
low resolutions and noise.
Model
The design of this model was founded on a fact discovered in the 20th century which
stipulated that spinal marrow contained some basic nervous system signals which generated
locomotion. According to the three authors, the nets of nervous cells on vertebrates which
produced rhythmic movements remained questionable. They, however, found out that the
nervous nets in the spinal marrow were capable of generating rhythmic movements such as

BIOMECHANICAL MODELING OF HUMAN GAIT 5
walking swimming and jumping when sequestered from sensorial entrances and brain. They
termed those specialized nervous systems as central pattern generators (CPGs) and which would
be responsible in controlling the human locomotion partially as evidenced in research by Xu,
Huang, Zeng, & Xu (2012) and Yahya, boukadi, Maamar & Abdallah (2015).The choice of an
appropriate locomotion pattern in this model depended on the combination of sensorial data, the
instructions on the determined motor conditions as well as the central programming. This
information was then used to determine the general organization of muscular synergy which
organizes for multiple conditions of gait and posture.
As shown in the figure above, the model comprised of a scheme of controlled systems of
human locomotion which were managed by the central nervous system and which would be
supplied with pattern curves of all the parts of the locomotor by the CPG. The information would
then be passed to all the muscles through a network of motoneurons while the conjoined
muscular activities perform the locomotion. The sensorial information regarding disturbances

BIOMECHANICAL MODELING OF HUMAN GAIT 6
and environmental conditions are supplied as system feedback in fast actions which proceed
from the CPG and which adapts gaits to new situations. CFGs are extensively used to analyze
biochemical and physiological modeling. Van der Pol oscillator has been used to demonstrate
the CFG model through the consideration of n coupled oscillators. From van der Pol equation:
Where p, £, and Ω are the parameters of an oscillator adding the coupling terms that denote the
velocities of the n oscillators, we get:
(2) Represents the coupling between the oscillators which have the same frequency and where θ
is the system degree of freedom. However, in a case where the coupling between the oscillators
has an integer relationship with the frequency, the equation would become:
Research 2: Bipedal human walking control derived from analysis of robotic locomotion
This paper proposed a bipedal robotic controller design where the coordination between
the motor output and the sensory input would be treated as a black box retrieved from the
human data. To achieve that, the four authors investigated the causal relationship between the
filter functions transforming the sensory-motor actions and the contact information from legs
to feet muscle when a human being is walking (De Boer, 2012). After establishing the
relationship, a robust and nonlinear control system was created and analyzed by matching it to

BIOMECHANICAL MODELING OF HUMAN GAIT 7
a bipedal robot in absence of any trajectory control or a central pattern generator. The end
results demonstrated that the controllers were capable of generating a stable robotic walk. This
was, therefore, an indication that multifaceted locomotion arrays could result from simple
models based on the reflexes and supports the principle that the strategies derived from human
gait control have prospective applications (De Boer, 2012).
Model
The model demonstrated the entire processing of EMG signals, XmXm (m = BF, RF,
TA, LG) and FSR signals FiFi [i = contralateral heel (CH), ipsilateral heel (IH), ipsilateral toe
(IT)], were used to get the estimated EMG output signals for all the muscles YmYm by the use
of a least mean squares (LMS) method through convolution of filter impulse
responses hm,ihm,i were FSR contacts the signal FiFi.
Ym=Fi∗hm,iYm=Fi∗hm,i
Error signals which are denoted by E would be calculated as the difference between EMG
signals XmXm and the projected EMG signals YmYm. So,
E=Xm−YmE=Xm−Ym

BIOMECHANICAL MODELING OF HUMAN GAIT 8
The filter coefficient would be updated by the optimization algorithm which is driven
by error signals. The filter response duration would be set to the length of the two strides
below (De Boer, 2012):
hm,i,p+1=hm,i+E⋅Fi⋅μhm,i,p+1=hm,i+E⋅Fi⋅μ.
μμ denoted the learning rate of the adaptive filters, which was set to 0.001.
In regard to EMG muscle signals, the diagram above was used to demonstrate how
those signals were related and elicited to the ground contact in a single complete gait cycle.
The characteristics of transfer function coefficients were identified conforming to the muscle
activities which promote joint movement when people are walking ( De Boer, 2012). The TA
function was presented with to have two peaks responsible plantarflexion of ankles at the heel
strike (HS) and the dorsiflexion when toes are off (TO), respectively. The LG peak produced
ankle push-off which is related to the heel off (HO) when walking. RF transfer function was

BIOMECHANICAL MODELING OF HUMAN GAIT 9
related to both hip flexion joint movement at TO and the knee extension when a hip reaches
the anterior extreme angle (AEA).
Research 3: Theoretical and computational model of the human gait to simulate
pathological patterns
In this analysis, the authors used the systematic quantification, interpretation of temporal
sequences and follow up movements that describe human locomotion. The analysis utilized a
collection of kinetic and kinematic data to describe angles, forces, and displacements on the
lower limb as well as its joints under the gait cycle (Cifuentes & la Portilla, 2012). The data was
retrieved from videos, force platforms and Electromyography (EMG) and analyzed as a clinical
report. This is despite the fact that the interpretation of dynamic patterns and human gait analysis
highly dependent on the specialist. To gain such an experience, the study suggested that
extensive training was a mandatory coupled with an interaction with a large number of patients
with different pathologies to allow the specialist to identify the features of different gait patterns
with a degree of certainty. As part of the strategy, models which described the dynamics of
normal and pathological gait were formulated and implemented (Cifuentes & la Portilla, 2012).
The four authors then came up with a computational model of a human gait that allowed them to
describe both pathological and normal movements using some simple representation of
biomechanics to describe the complete CoG displacement and the inverse kinetic approach of
obtaining clinical gait description.
Model
The model used in this paper was a biped model that simplified the structure of the
human body using a simple mechanical analogy of an inverted pendulum. The rigid structures

BIOMECHANICAL MODELING OF HUMAN GAIT
10
that appear to support the body mass (m) in the model represent the legs (Cifuentes & la Portilla,
2012).
According to the model, the path marked by the inverted pendulum approximates the
normal movement of a human body and can be expressed mathematically as ˙θ(t) = g l cosθ1 ,
because it generated a semicircular movement to approximate the CoG observed in gait
laboratories and which have not been described by any non-linear human movement before
(Cifuentes & la Portilla, 2012). The model introduced a direct relationship between pathological
and normal gaits based on the passive dynamic theory which states that gait dynamics can be
defined using structural relationships that indicate the important role of muscle strength and the
control put forth by the nervous system to ensure an efficient movement which is observed in a
normal gait. The model represented the body as a double inverted pendulum where the trunk
represented the body mass while the feet were represented by the two masses separated by the
rigid structure which represented the legs and that closely related to the slope of the ramp. To
compute β as shown in the model they used the formula β = m M ≈ 0 which could be simplified
into the classical inverted pendulum equations as shown below (Cifuentes & la Portilla, 2012)

BIOMECHANICAL MODELING OF HUMAN GAIT
11
To describe the human gait, the equation above was reduced into a set of dynamic patterns which
led to the relationship below (Cifuentes & la Portilla, 2012):
Simulation of the heel strike was also factored in through the introduction of the restriction rule,
φ(t) = 2θ(t), during the gait cycle given by (Cifuentes & la Portilla, 2012):
This allowed for support gait exchange during leg balancing. The mass ratio was however
ignored during the movement to reduce the dimensions of the model. Lastly, the model was
modified by the four authors through the addition of variables that described the angular
momentum occurring on the hips whenever heel striking was taking place (Cifuentes & la
Portilla, 2012).
Research 4: On automated model-based extraction and analysis of gait
This study aimed at coming up with an automated non-invasive model in order to identify

BIOMECHANICAL MODELING OF HUMAN GAIT
12
people based on their walking and running traits. This was achieved through leg motion analysis
as well as the analysis on the limb angles (Wagg & Nixon, 2004). Through the model, people
could be recognized not only when walking but also when running.
Model
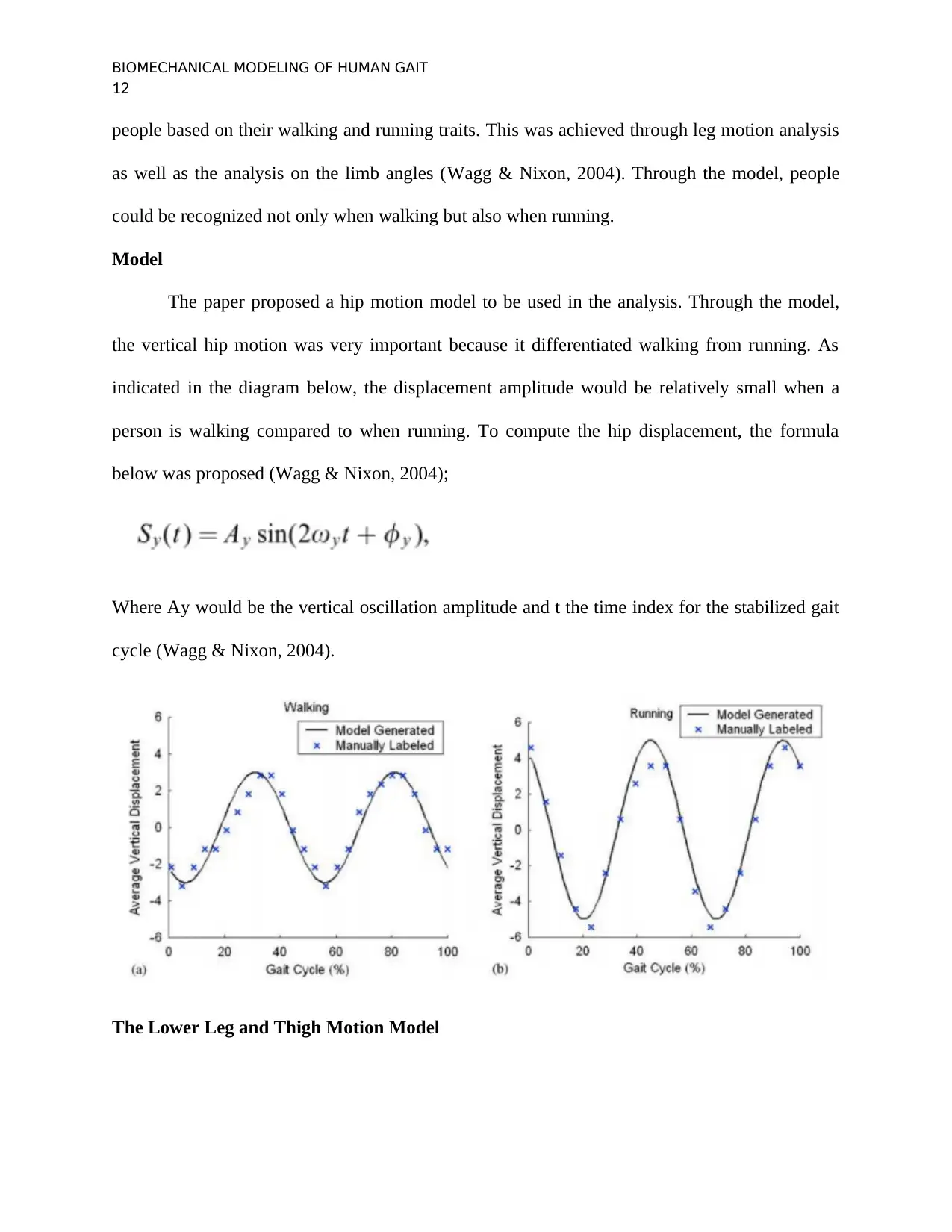
The paper proposed a hip motion model to be used in the analysis. Through the model,
the vertical hip motion was very important because it differentiated walking from running. As
indicated in the diagram below, the displacement amplitude would be relatively small when a
person is walking compared to when running. To compute the hip displacement, the formula
below was proposed (Wagg & Nixon, 2004);
Where Ay would be the vertical oscillation amplitude and t the time index for the stabilized gait
cycle (Wagg & Nixon, 2004).
The Lower Leg and Thigh Motion Model

BIOMECHANICAL MODELING OF HUMAN GAIT
13
The obvious movement of the legs has its basis on the model development and was to be
computed using the formula below (Wagg & Nixon, 2004)
The two models had some promising recognition results and could be used on noisy and low-
resolution images which in most of the models affected the recognition results (Wagg & Nixon,
2004).
Research 5: Automatic Gait Recognition by Symmetry Analysis
The authors of this paper described a new method which they saw useful for automatic
recognition of gait based on the analysis of human motion symmetry using a generalized
symmetry operator. The generalized symmetry operator could locate the features of a human
gait based on their symmetrical properties with no reference to shape borders or the general
appearance (Hayfron-Acquah, Nixon & Carter, 2003). The approach was supported by
psychologists’ view that human gait has a symmetrical motion pattern. The authors applied
new methods to different databases and were able to derive gait signatures for optical flow and
silhouettes. From the model analysis, it was observed that individual symmetry gait properties
are unique and could indeed be used to recognize a person ( Hayfron-Acquah, Nixon & Carter,
2003). The model also indicated a promising recognition success rate of 95% and with a
performance analysis suggesting that symmetry enjoys a practical advantage of relative
immunity to missing frames and noise and also has the ability to handle occlusion.
Model
Based on the fact that Symmetry is the fundamental property suggesting the important
principle of perception and objects are said to be symmetric if their shapes are invariant to the

BIOMECHANICAL MODELING OF HUMAN GAIT
14
application of symmetric operations, this model has used the Boolean symmetry operations to
assess human gait (Hayfron-Acquah, Nixon & Carter, 2003). To extract a human body in
motion, feature templates would be extracted from the gait sequence to obtain template
sequences. The symmetry operator would thereafter use the edge map of the images in the
sequence to ascribe symmetry magnitudes and orientation to the image points which could be
accumulated at the midpoint of all pairs of points as shown below (Hayfron-Acquah, Nixon &
Carter, 2003).
Research 6: Gait Recognition without Subject Cooperation
In their research, the authors of this paper suggested an approach that would involve a
selection of gait feature to work on gallery pair selection basis and probe gait sequencing by the
use of Gait Entropy Image (GEnI) (Bashir, Xiang & Gong, 2010). The model would also

BIOMECHANICAL MODELING OF HUMAN GAIT
15
incorporate selection features based on Adaptive Components and Discriminant Analysis
(ACDA) in a robust and fast recognition against the changes in appearance. In simple terms, the
method was based on computing Shannon entropy of pixels over gait full motions by
differentiating dynamic and static pixels of a Gait Entropy Image (GEI) model to extract
silhouette from the different frames which were applied after the horizontal alignment and
normalization of all the frames which were extracted (Bashir, Xiang & Gong, 2010). The gait
motions were then differentiated by estimating their frequencies using a maximum entropy
estimation technique. The Gait Energy Image (GEI) would then be calculated afterward, using
the following formula below.
Where T denoted the total frames in full gait motion while I denoted the silhouette image with
pixel coordinates represented by x and y. The model clearly differentiated static and dynamic
areas of Gait Energy Image (GEI) through the evaluation of Shannon entropy of each and every
pixel (Bashir, Xiang & Gong, 2010). Shannon entropy measured the ambiguity linked with the
random variables when the gait cycle was full gait cycle and could be calculated in a Gait
Entropy Image (GEnI) shown in the formula below

BIOMECHANICAL MODELING OF HUMAN GAIT
16
Where y and x are the coordinates of the pixel while pk (x,y) is the probability of the pixel taken
on the kth value (Bashir, Xiang & Gong, 2010)
Summary
From the above scrutiny, it’s without any reasonable doubt that gait analysis is becoming
an unobtrusive and a promising biometric measure that is currently attracting many researchers.
Its application areas include but not limited to intelligent services and surveillance which entail
the identification of people from a distance based on their gait traits. In the past, it was seen as a
triggering factor in the gait analysis sector where scientists could manage to differentiate people
based on their walking and running styles using silhouette methods. Following the increasing
interest in the sector, researchers have come up some additional advanced models such as Patch
Distribution Feature (PDF) model which has combined the Regularized Locally Tensor
Discriminant Analysis (RLTDA) and Enhanced Gabors (EG) as well as the Gait Energy Images
(GEI) as a collection of augmented Gabor feature to enhance the evaluation of human gait.
Moving forward, the Hip motion model is introduced, an important model through which the
vertical hip motion can be differentiated on a person walking or running. As a backup to this
model, an automated non-invasive model has also been introduced with an aim of identifying
people based on their walking and running traits. This was achieved through leg motion analysis
as well as the analysis on the limb angles. Through the model, people could be recognized not
only when walking but also when running. Another interesting model named introduced in this

BIOMECHANICAL MODELING OF HUMAN GAIT
17
paper was the biped model, a model that simplified the structure of the human body using a
simple mechanical analogy of an inverted pendulum. Among them, the automated non-invasive
model which had the capability of identifying people based on their walking and running traits
and another model which is lower leg and thigh motion model stood out as the best models
because of their excellent ability to recognize results and also could easily be used in
environments which were noisy to capture low-resolution images which in most of the models
proved to negatively affect the recognition results largely.
References
Bashir, K., Xiang, T., & Gong, S. (2010). Gait recognition without subject cooperation. Pattern
Recognition Letters, 31(13), 2052-2060.
Cifuentes De la Portilla, C (2012). A theoretical and computational model of the human gait to
simulate pathological patterns(Doctoral dissertation, Universidad Nacional de
Colombia).
Dupuis, Y., Savatier, X., & Vasseur, P. (2013). Feature subset selection applied to model-free
gait recognition. Image and vision computing, 31(8), 580-591.
De Boer, T. (2012). Foot placement in robotic bipedal locomotion.
Hayfron-Acquah, J. B., Nixon, M. S., & Carter, J. N. (2003). Automatic gait recognition by
symmetry analysis. Pattern Recognition Letters, 24(13), 2175-2183.
Hu, M., Wang, Y., Zhang, Z., Zhang, D., & Little, J. J. (2013). Incremental learning for video-
based gait recognition with LBP flow. IEEE transactions on cybernetics, 43(1), 77-89.

BIOMECHANICAL MODELING OF HUMAN GAIT
18
Lishani, A. O., Boubchir, L., Khalifa, E., & Bouridane, A. (2017). Human gait recognition based
on Haralick features. Signal, Image and Video Processing, 11(6), 1123-1130.
Nandy, A., & Chakraborty, P. (2017). A study on human gait dynamics: modeling and
simulations on the OpenSim platform. Multimedia Tools and Applications, 76(20),
21365- 21400.
Wagg, D. K., & Nixon, M. S. (2004, May). On automated model-based extraction and analysis
of gait. In null (p. 11). IEEE.
Xu, Y. Huang, Z. Zeng, & X. Xu (2012), Human Gait Recognition Using Patch Distribution
Feature and Locality-Constrained Group Sparse Representation, vol. 21, no. 1, pp. 316–
326.
Yahya, K. boukadi, Z. Maamar, & H. Ben Abdallah (2015), Enhancing Business Processes with
Web 2.0 Features, Proc. 12th Int. Conf. E-bus., pp. 183–190.
Yam, C., Nixon, M. S., & Carter, J. N. (2004). Automated person recognition by walking and
running via model-based approaches. Pattern Recognition, 37(5), 1057-1072.