Project: Vibration Analysis and Mechanical Efficiency of IC Engine

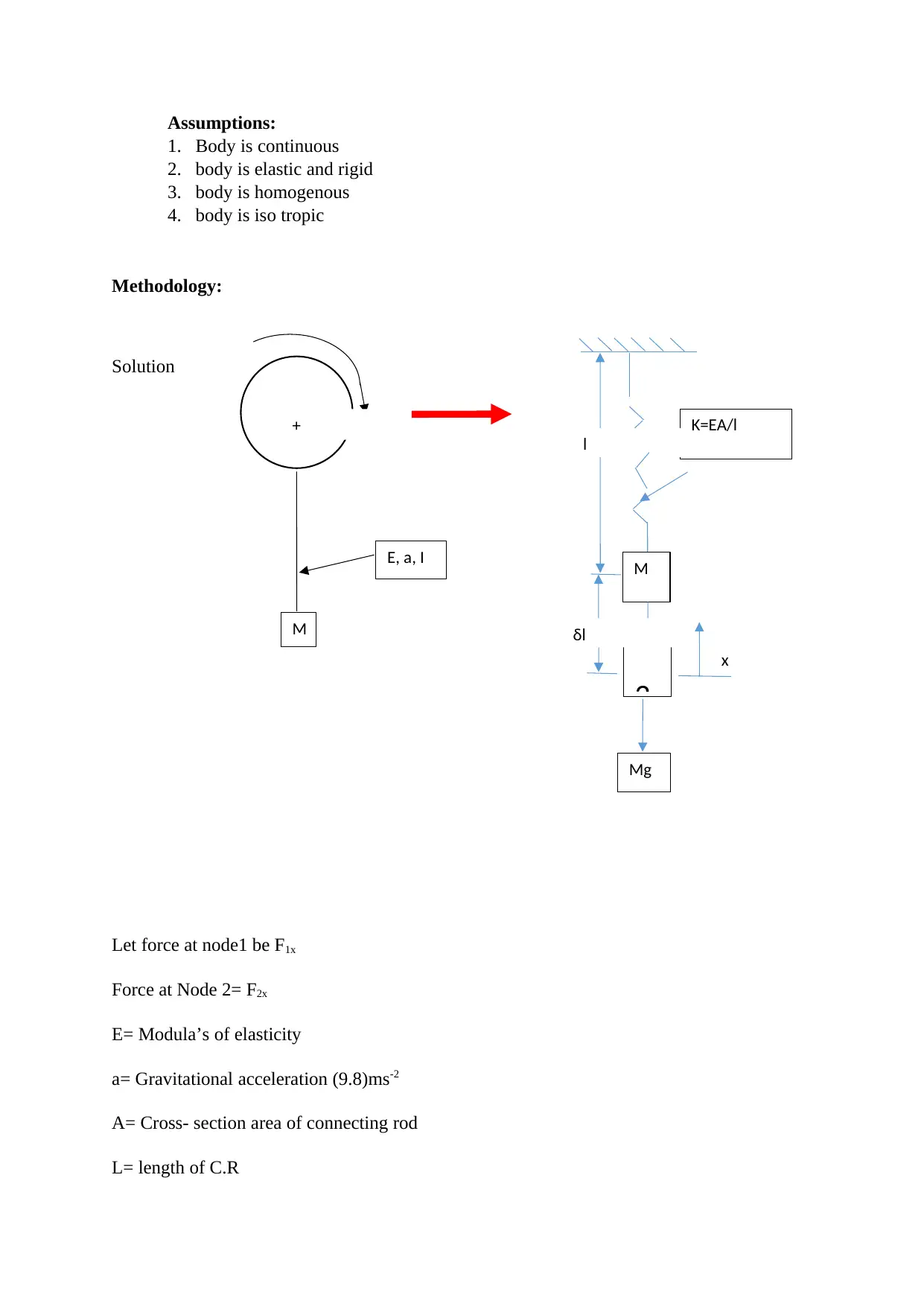
This project analyzes the impact of vibration on the mechanical efficiency of an internal combustion engine. The study utilizes both analytical and numerical approaches, with a focus on the finite element method (FEM) to calculate strain, deflection, and vibration frequency within the engine system. The vibration frequency is then used to determine friction losses, ultimately leading to the calculation of the engine's mechanical efficiency. The project includes detailed assumptions, a clear methodology section outlining the FEM approach, and a case study centered on a 125cc two-stroke engine. Key calculations involve stiffness matrix derivation, strain and displacement analysis, and friction power determination. The conclusion highlights the impact of vibration on efficiency and material properties like fracture toughness, emphasizing the importance of damping systems and friction reduction strategies. This work provides a comprehensive overview of vibration's influence on engine performance and efficiency.

Internal Combustion Engines
[Document subtitle]
[DATE]
[Company name]
[Company address]

Table of content
1. Introduction.
2. Assumptions.
3. Methodology.
4. Case study.
5. Conclusion.
6. References.

Abstract
The paper deals with the effect of vibration on the mechanical efficiency of the engine. It
involves analytical and numerical approach to solve the problems relating to vibration. Finite
Element method analysis has been done on the engine to calculate strain, deflection and the
frequency of vibration of the system. Now the vibration frequency is further used to calculate
the losses in the engine when engine is in dynamic condition. At last mechanical efficiency of
engine has been calculated.
Introduction
1. Engine:- It is a device comprising of the linkages which converts on form of energy
into mechanical work. The input energy may in form of some chemical reactions, heat
energy, electricity etc. The paper deals only with the internal combustion engine.
Based upon operating principles an IC engine is classified as 2 stroke and 4 stroke
engine. An ideal engine generally works in following steps:-
1. Suction.
2. Isentropic Compression.
3. Heat addition.
4. Isentropic expansion.
5. Heat rejection.
In the cycle only the way of heat rejection differs the cycle.
When heat addition takes place at constant volume the cycle is known as the Otto Cycle.
When heat addition takes place at constant pressure the cycle is known as the Diesel Cycle.
When heat addition takes place first at constant volume and then at constant pressure the
cycle is known as the Dual Cycle.
During working engine will be at dynamic condition and produces vibration. This vibration
causes decrease in efficiency of engine due to increase in friction losses.
2. Vibration:- It is defined as to and fro motions of a body about their equilibrium
positions. There are two types of mechanical vibration:-
1. Harmonic.
2. Oscillation.
The vibrations in which there is no kinetic friction at all as well as there is no external force
after the initial release of the system are known as natural vibration. If there is any micro-
crack present at the system than due to vibration this crack may propagate and results in
system failure.
In this paper the piston cylinder arrangement is assumed as spring mass system where piston
is considered as rigid mass and connecting rod as spring. By the use of FEM stiffness of
spring is derived and further strain, displacement of mass and strain is calculated. Due to
vibration there are some friction losses occurred in the system. These friction losses are
calculated by using the frequency of vibration term and further mechanical frequency is
calculated.

Assumptions:
1. Body is continuous
2. body is elastic and rigid
3. body is homogenous
4. body is iso tropic
Methodology:
Solution
Let force at node1 be F1x
Force at Node 2= F2x
E= Modula’s of elasticity
a= Gravitational acceleration (9.8)ms-2
A= Cross- section area of connecting rod
L= length of C.R
M
+
E, a, I M
2
Mg
K=EA/l
x
l
δl

By Method of FEM
Stiffness matrix of above system is
K1 = AE/l
K12= k 1 −k 1
−k 1 k 1
Let displacement of 1 be d1x & for node 2 be d2x
[F] = [k][d]
F 1 x
F 2 x = k 1 −k 1
−k 1 k 1
d 1 x
d 2 x
F 1 x
mg = k 1 −k 1
−k 1 k 1
d 1 x
d 2 x
Mg= (-k1 x 0) + (d2x)
D2x = Mg/K1
=Mgl/AE
Strain = x
l [-1 1]
d 1 x
d 2 x
Strain = x
l xd2x = Mgl/AEL= Mg/AE
Strain= l−δl
l =1- δl
l
δl = (1-ɛ)l = l- Mg/AE
Where M = mass of the piston
Frequency of system f= 1
2 π √ K 1
M
f= 1
2 π √ AE
Ml CITATION Dav03 \l 16393 (Hutton, 2003)
Considering of 125 cc 2 stroke
Global stiffness matrix

Case study:
Engine cc- 124.7cc
No. of cylinder =1
Max. Brake Power = 9 BHP
At Nmax= 7000 rpm
Max. Torque = 10.35 at N= 4000rpm.
Material of Piston= Aluminium A390-T5
Modula’s of elasticity E = 81.2Gpa
Density of elasticity ρ = 20°c = 2730 kgm-3
Mass of piston = density x engine cc
M = ρ x engine cc
M= 2730 x (124.77 x 10-6) = 0.3406kg
Cross sectional
D = piston dia = 63 mm
A = cross sectional area of piston = π
4 x d2
A = π
4 x (6.3 X 10-3 )2 = 3.117 x 10-3 m2
Indicate power = Brake Power loss is due to vibration and other wanted factors
Frequency fn = 1
2 π x √ k 1
M
K1 = AE/l
Connecting rod length l = 110mm =0.11
K1 = AE
l = fn = 3.117 X 103
¿
0.1 ¿ X 81.2 X 10^9
K1 = 23.01 X 108 Nm-1

fn = 1
2 π x √ 23.1 X 103 0
0.3406 = 13081.45704 S-1
n = no. of revolutions
Friction force =μN = μmg = 0.25 x 0.3406 x 9.81
Ff= 0.8353N
Friction power = Ff X ωn = Ff X 2πfn x r (r= crank radius)
Fp = 0.8353 x 2π x 13081.4570 x 0.04
Fp = 2746.24 watt
Bp =9 x 735 = 6615 watts
Ip = BP + fp = 6615 + 2746.24 = 9361.24watt
η = efficiency
% η = BP
IP x 100 = 6615
9361.24 x 100= 70%
η = 70% at max speed
so η can be increased by decreasing the coefficient of friction of the piston cylinder.
Conclusion: From the above analysis it is clear that due to vibration there are friction losses.
Apart from this some material property such as fracture toughness also gets affected. For
system working in dynamic environment surface hardness and fracture toughness both are
very important. During vibration if there is some micro crack present in the system which
may be due to manufacturing defect than this micro-crack propagates and causes problem.
Engine efficiency can be increased by decreasing friction and other minor losses. For engine
to stop vibrating proper damping system must be installed so that vibration losses can be
minimized.
References
Hutton, D. V., 2003. Fundamentals of Finite Element Analysis. New York City: McGraw-
Hill, 2003.