International Financial Management Report: Financial Analysis

This report delves into the core concepts of international financial management (IFM), exploring topics such as expected Net Present Value (NPV), standard deviation of NPV, and Internal Rate of Return (IRR). The report analyzes financial decisions within an international context, including capital budgeting, risk management, and the impact of privatization on financial performance. It examines cash flow analysis, probability of avoiding liquidation, and the ranking of investment projects based on financial metrics. The analysis incorporates numerical examples and calculations to illustrate key concepts and provide insights into making informed financial decisions. The report also compares and contrasts NPV and IRR, and calculates the probability of negative NPV under varying conditions. This report serves as a comprehensive guide to understanding and applying IFM principles.

International Financial Management
1

Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY...................................................................................................................................3
Question 1........................................................................................................................................3
Question 2........................................................................................................................................5
Question 3......................................................................................................................................10
Conclusion.....................................................................................................................................14
REFERENCES..............................................................................................................................15
2

INTRODUCTION
Main objective of this report is to understand the concept of international financial
management which is also known as the international finance. It is related to the management of
finance in an international business environment. Main objective of international finance
management is to maximize the shareholders wealth (Andreeva and et. al. 2018). An
international finance manager will require to effectively study the concept of exchange rate and
currency markets, various risk such as political, exchange rate risk, interest rate risk, various risk
management techniques, cost of capital and capital budgeting in international context, working
capital management, balance of payment and so on. With the increase in globalization
entrepreneurs are free to operate their business in any corner of world (Shapiro and Hanouna,
2019). There are various factors which play an important role in international finance
management such as cross-boarder sharing, multi-currency shares, currency swaps, foreign
mutual funds and so on. This report includes various aspects of financial management through
different numeric task such as expected NPV, standard deviation of NPV, Net present value and
internal rate of return.
MAIN BODY
Question 1
a. The expected NPV:
Expected net present value refers to a capital budgeting technique which helps in
adjusting uncertainty and effectively calculating the net present value under various different
situations and profitability (Angrick, 2018). It helps in predicting future outcome and it provide
more accurate result as compare to traditional NPV method. It is a method of capital budget
which provide effective weightage for identifying the best net present value. It is a method which
is used for effective finance analysis which determine the feasibility of investment in a particular
project or business. This define the present value of future cash flow as compared to initial
investment of investors. In this method instead of depending on a single net present value
company calculate NPV under different situations such as best case, worst case, base case,
estimated profit of each scenario, weights of NPV are calculated according to related
probabilities and the expected NPV is find out. Expected NPV is the sum of total products of net
3

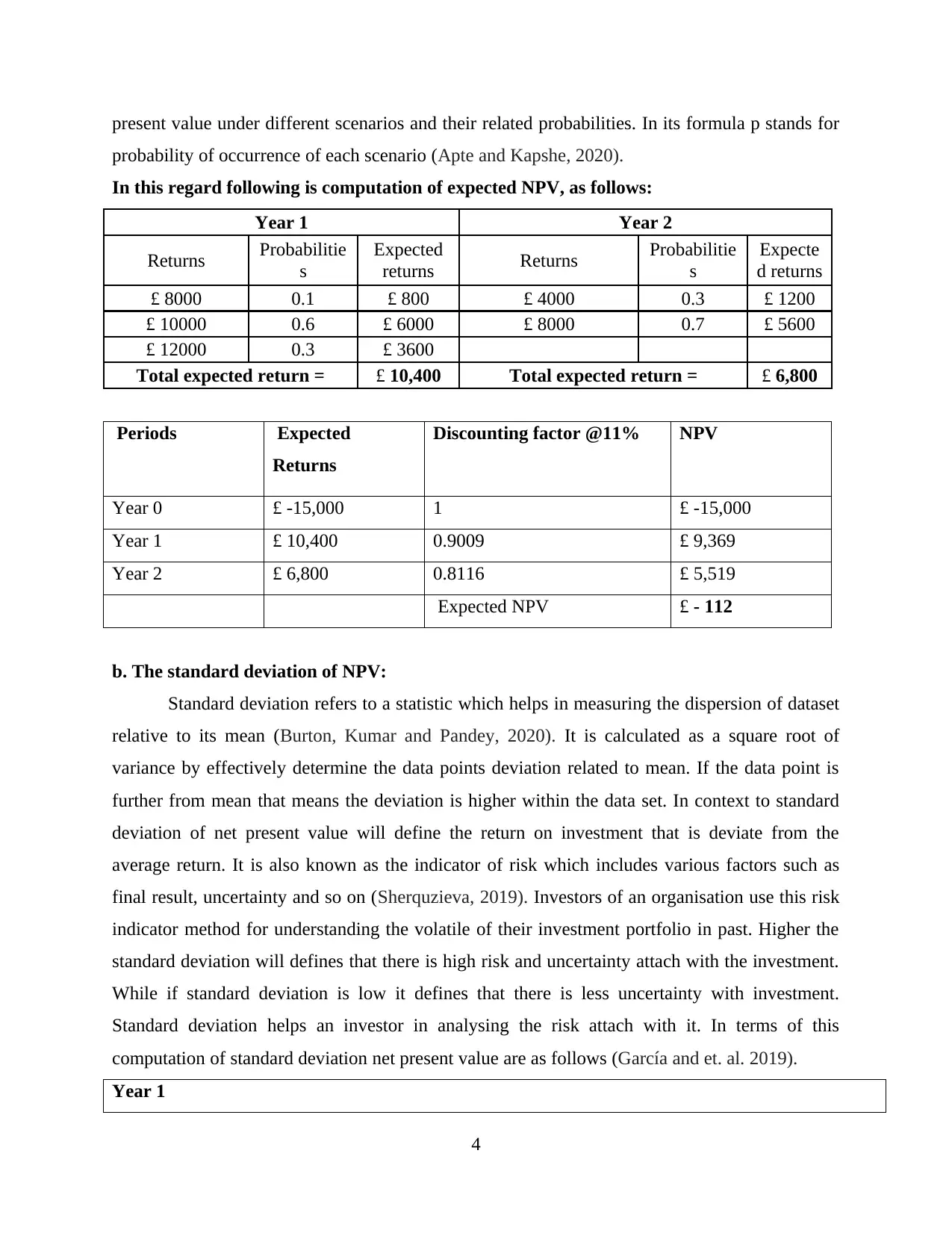
present value under different scenarios and their related probabilities. In its formula p stands for
probability of occurrence of each scenario (Apte and Kapshe, 2020).
In this regard following is computation of expected NPV, as follows:
Year 1 Year 2
Returns Probabilitie
s
Expected
returns Returns Probabilitie
s
Expecte
d returns
£ 8000 0.1 £ 800 £ 4000 0.3 £ 1200
£ 10000 0.6 £ 6000 £ 8000 0.7 £ 5600
£ 12000 0.3 £ 3600
Total expected return = £ 10,400 Total expected return = £ 6,800
Periods Expected
Returns
Discounting factor @11% NPV
Year 0 £ -15,000 1 £ -15,000
Year 1 £ 10,400 0.9009 £ 9,369
Year 2 £ 6,800 0.8116 £ 5,519
Expected NPV £ - 112
b. The standard deviation of NPV:
Standard deviation refers to a statistic which helps in measuring the dispersion of dataset
relative to its mean (Burton, Kumar and Pandey, 2020). It is calculated as a square root of
variance by effectively determine the data points deviation related to mean. If the data point is
further from mean that means the deviation is higher within the data set. In context to standard
deviation of net present value will define the return on investment that is deviate from the
average return. It is also known as the indicator of risk which includes various factors such as
final result, uncertainty and so on (Sherquzieva, 2019). Investors of an organisation use this risk
indicator method for understanding the volatile of their investment portfolio in past. Higher the
standard deviation will defines that there is high risk and uncertainty attach with the investment.
While if standard deviation is low it defines that there is less uncertainty with investment.
Standard deviation helps an investor in analysing the risk attach with it. In terms of this
computation of standard deviation net present value are as follows (García and et. al. 2019).
Year 1
4

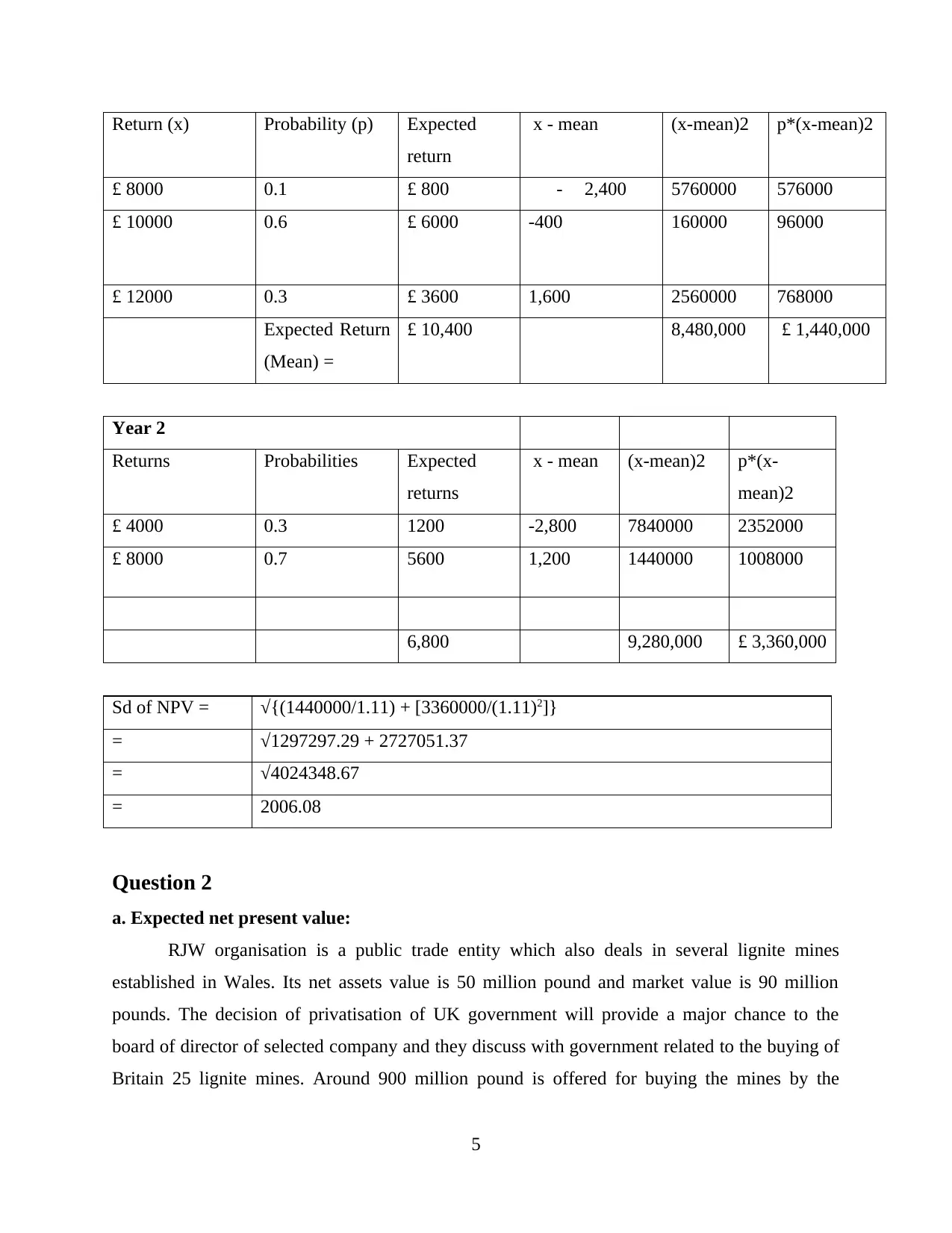
Return (x) Probability (p) Expected
return
x - mean (x-mean)2 p*(x-mean)2
£ 8000 0.1 £ 800 - 2,400 5760000 576000
£ 10000 0.6 £ 6000 -400 160000 96000
£ 12000 0.3 £ 3600 1,600 2560000 768000
Expected Return
(Mean) =
£ 10,400 8,480,000 £ 1,440,000
Year 2
Returns Probabilities Expected
returns
x - mean (x-mean)2 p*(x-
mean)2
£ 4000 0.3 1200 -2,800 7840000 2352000
£ 8000 0.7 5600 1,200 1440000 1008000
6,800 9,280,000 £ 3,360,000
Sd of NPV = √{(1440000/1.11) + [3360000/(1.11)2]}
= √1297297.29 + 2727051.37
= √4024348.67
= 2006.08
Question 2
a. Expected net present value:
RJW organisation is a public trade entity which also deals in several lignite mines
established in Wales. Its net assets value is 50 million pound and market value is 90 million
pounds. The decision of privatisation of UK government will provide a major chance to the
board of director of selected company and they discuss with government related to the buying of
Britain 25 lignite mines. Around 900 million pound is offered for buying the mines by the
5

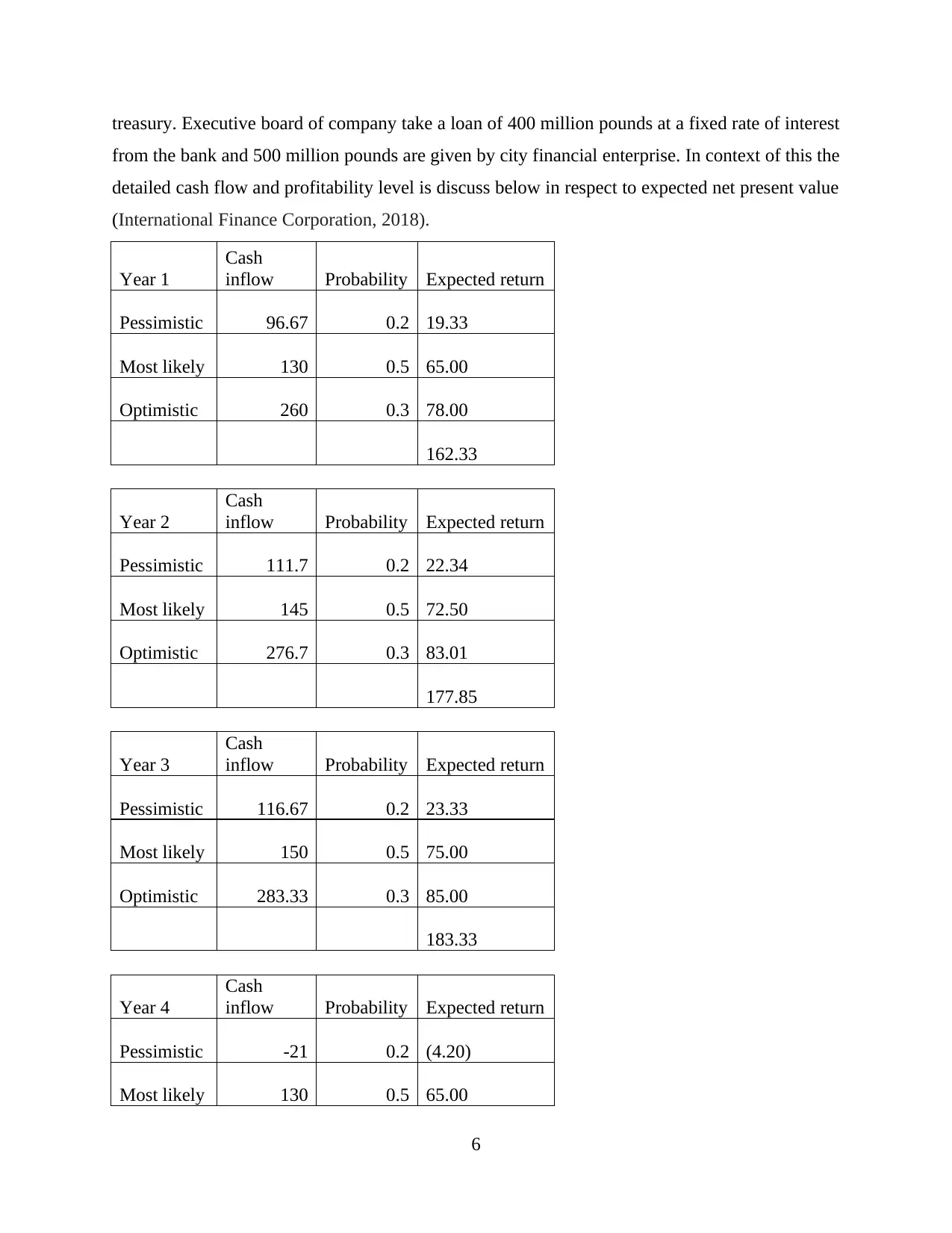
treasury. Executive board of company take a loan of 400 million pounds at a fixed rate of interest
from the bank and 500 million pounds are given by city financial enterprise. In context of this the
detailed cash flow and profitability level is discuss below in respect to expected net present value
(International Finance Corporation, 2018).
Year 1
Cash
inflow Probability Expected return
Pessimistic 96.67 0.2 19.33
Most likely 130 0.5 65.00
Optimistic 260 0.3 78.00
162.33
Year 2
Cash
inflow Probability Expected return
Pessimistic 111.7 0.2 22.34
Most likely 145 0.5 72.50
Optimistic 276.7 0.3 83.01
177.85
Year 3
Cash
inflow Probability Expected return
Pessimistic 116.67 0.2 23.33
Most likely 150 0.5 75.00
Optimistic 283.33 0.3 85.00
183.33
Year 4
Cash
inflow Probability Expected return
Pessimistic -21 0.2 (4.20)
Most likely 130 0.5 65.00
6

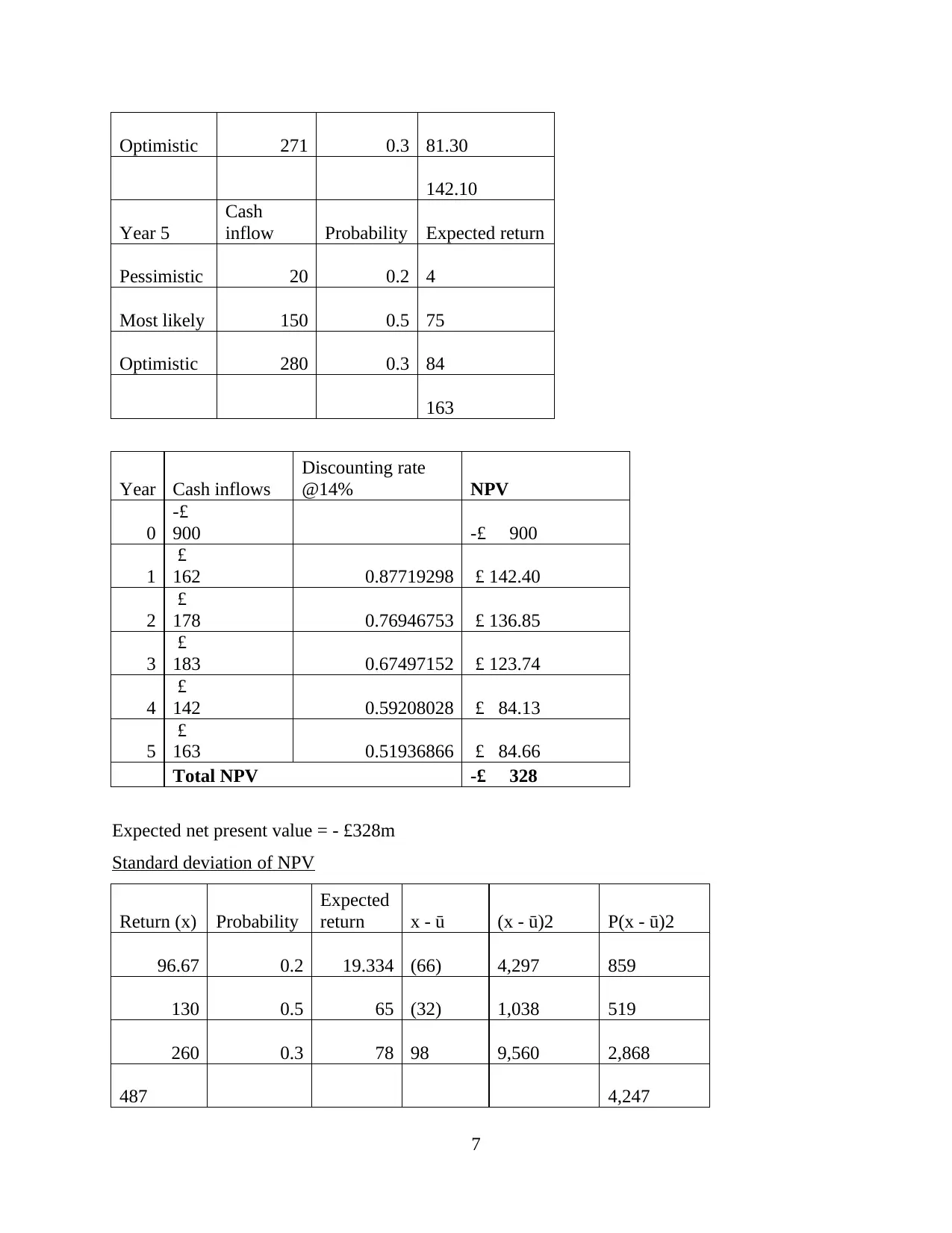
Optimistic 271 0.3 81.30
142.10
Year 5
Cash
inflow Probability Expected return
Pessimistic 20 0.2 4
Most likely 150 0.5 75
Optimistic 280 0.3 84
163
Year Cash inflows
Discounting rate
@14% NPV
0
-£
900 -£ 900
1
£
162 0.87719298 £ 142.40
2
£
178 0.76946753 £ 136.85
3
£
183 0.67497152 £ 123.74
4
£
142 0.59208028 £ 84.13
5
£
163 0.51936866 £ 84.66
Total NPV -£ 328
Expected net present value = - £328m
Standard deviation of NPV
Return (x) Probability
Expected
return x - ū (x - ū)2 P(x - ū)2
96.67 0.2 19.334 (66) 4,297 859
130 0.5 65 (32) 1,038 519
260 0.3 78 98 9,560 2,868
487 4,247
7

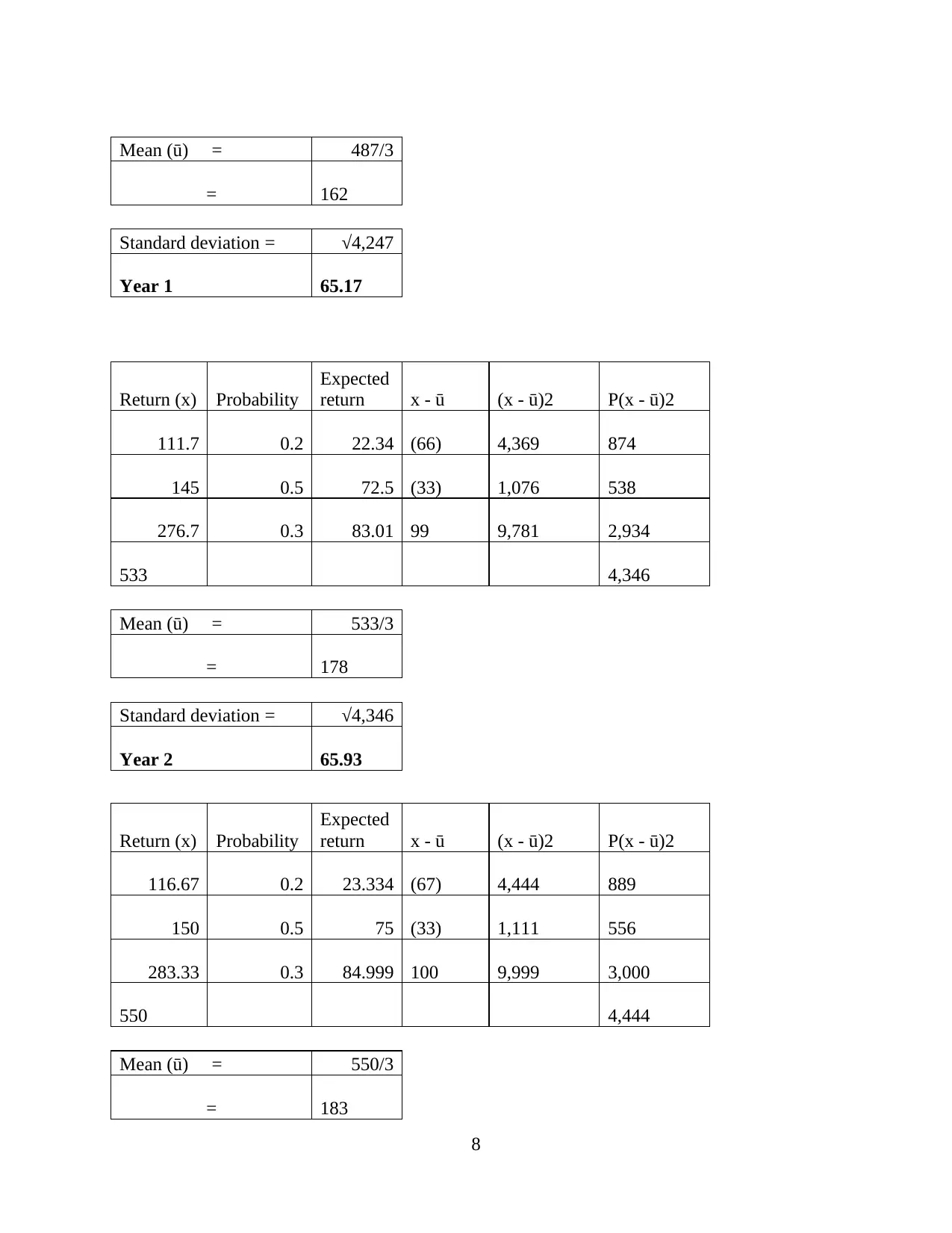
Mean (ū) = 487/3
= 162
Standard deviation = √4,247
Year 1 65.17
Return (x) Probability
Expected
return x - ū (x - ū)2 P(x - ū)2
111.7 0.2 22.34 (66) 4,369 874
145 0.5 72.5 (33) 1,076 538
276.7 0.3 83.01 99 9,781 2,934
533 4,346
Mean (ū) = 533/3
= 178
Standard deviation = √4,346
Year 2 65.93
Return (x) Probability
Expected
return x - ū (x - ū)2 P(x - ū)2
116.67 0.2 23.334 (67) 4,444 889
150 0.5 75 (33) 1,111 556
283.33 0.3 84.999 100 9,999 3,000
550 4,444
Mean (ū) = 550/3
= 183
8

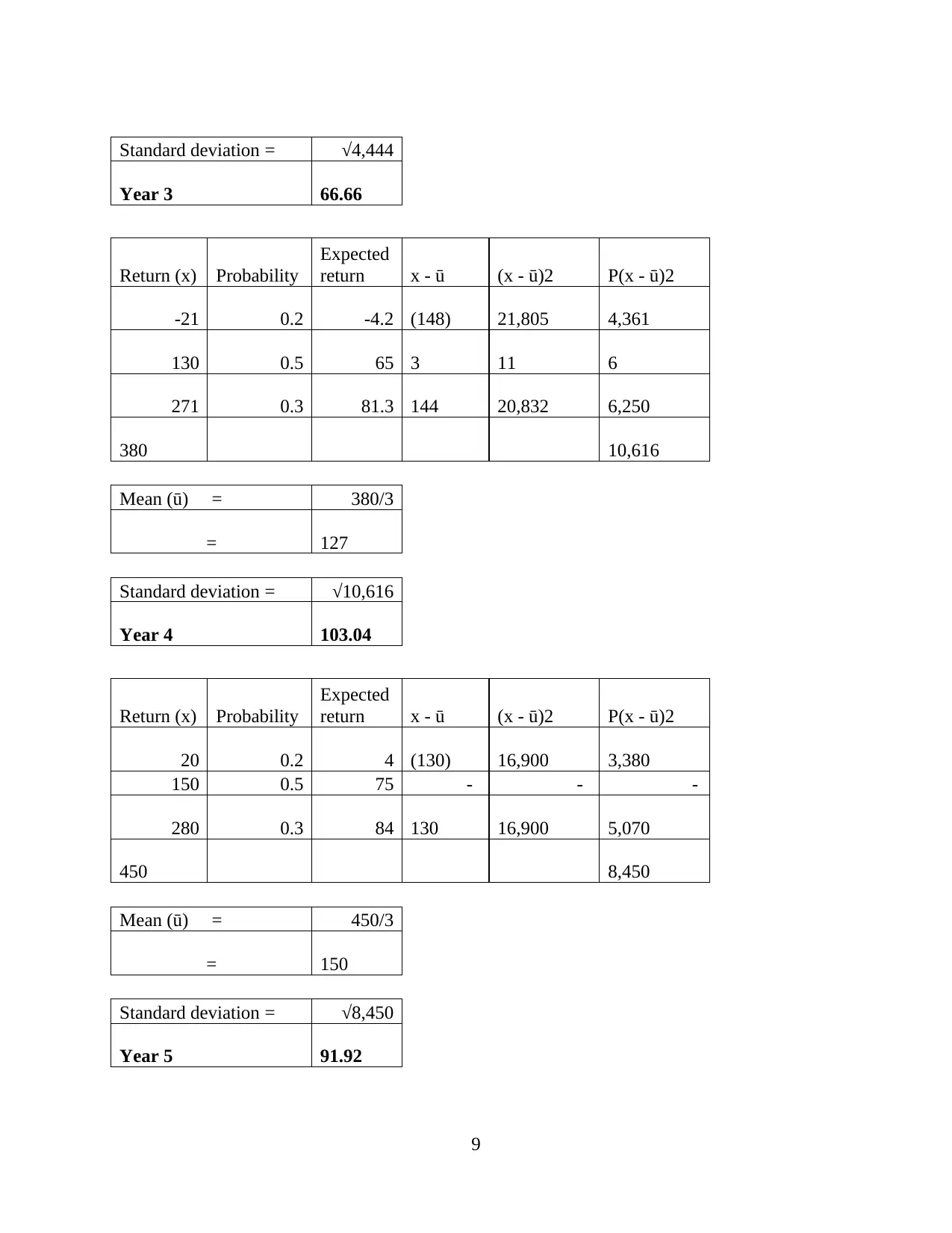
Standard deviation = √4,444
Year 3 66.66
Return (x) Probability
Expected
return x - ū (x - ū)2 P(x - ū)2
-21 0.2 -4.2 (148) 21,805 4,361
130 0.5 65 3 11 6
271 0.3 81.3 144 20,832 6,250
380 10,616
Mean (ū) = 380/3
= 127
Standard deviation = √10,616
Year 4 103.04
Return (x) Probability
Expected
return x - ū (x - ū)2 P(x - ū)2
20 0.2 4 (130) 16,900 3,380
150 0.5 75 - - -
280 0.3 84 130 16,900 5,070
450 8,450
Mean (ū) = 450/3
= 150
Standard deviation = √8,450
Year 5 91.92
9

Standard deviation of NPV = Year 1 + Year 2 + Year 3 + Year 4 + Year 5
= 65.17 + 65.93 + 66.66 + 103.04 + 91.92
= £392.72 Million
b. Probability of avoiding liquidation
Value of Mean NPV = - £328m
Standard deviation = 392.72
Applying the normal distribution:
Probability (x < -£550m):
P (x < -£550m) = - 0.57
Value here of -0.57 in the z table is 0.28434 or 28.43% chance to avoid liquidity.
c. Probability of NPV greater than £100m
NPV mean value = - £328m
Standard deviation = 392.72
Applying here normal distribution:
Probability of the avoiding liquidation that is (x > £100m):
P(x > £100m) = 1 - P(x < £100m)
= 1 –
= 1 – 1.089
= - 0.09
Value of Z = 0.4641 or 46.41%
Question 3
a. Rank of the projects
Years
Project 0 1 2 3 4 5 NPV
A
£
(500,000)
£
600,000
B £ £ £
10

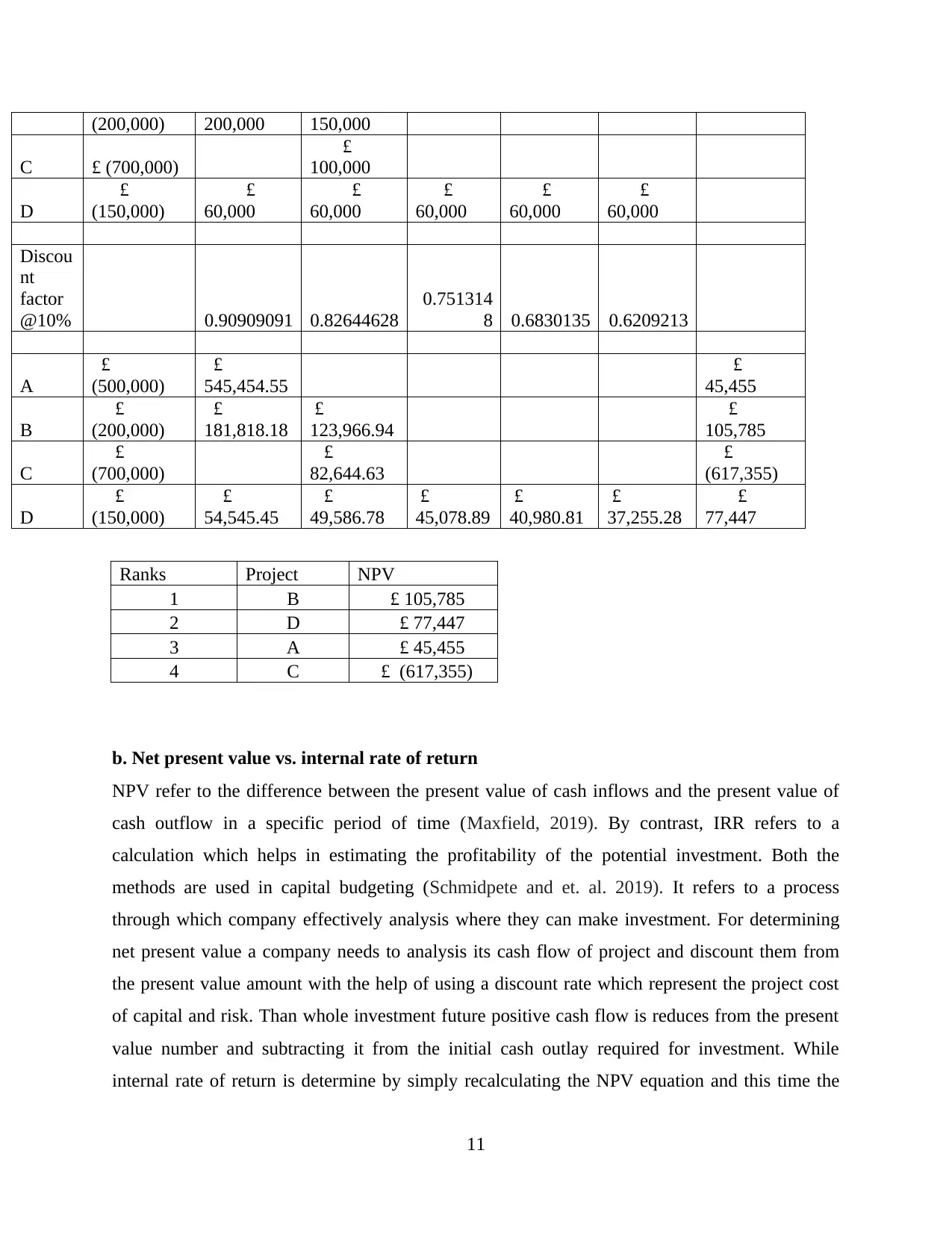
(200,000) 200,000 150,000
C £ (700,000)
£
100,000
D
£
(150,000)
£
60,000
£
60,000
£
60,000
£
60,000
£
60,000
Discou
nt
factor
@10% 0.90909091 0.82644628
0.751314
8 0.6830135 0.6209213
A
£
(500,000)
£
545,454.55
£
45,455
B
£
(200,000)
£
181,818.18
£
123,966.94
£
105,785
C
£
(700,000)
£
82,644.63
£
(617,355)
D
£
(150,000)
£
54,545.45
£
49,586.78
£
45,078.89
£
40,980.81
£
37,255.28
£
77,447
Ranks Project NPV
1 B £ 105,785
2 D £ 77,447
3 A £ 45,455
4 C £ (617,355)
b. Net present value vs. internal rate of return
NPV refer to the difference between the present value of cash inflows and the present value of
cash outflow in a specific period of time (Maxfield, 2019). By contrast, IRR refers to a
calculation which helps in estimating the profitability of the potential investment. Both the
methods are used in capital budgeting (Schmidpete and et. al. 2019). It refers to a process
through which company effectively analysis where they can make investment. For determining
net present value a company needs to analysis its cash flow of project and discount them from
the present value amount with the help of using a discount rate which represent the project cost
of capital and risk. Than whole investment future positive cash flow is reduces from the present
value number and subtracting it from the initial cash outlay required for investment. While
internal rate of return is determine by simply recalculating the NPV equation and this time the
11

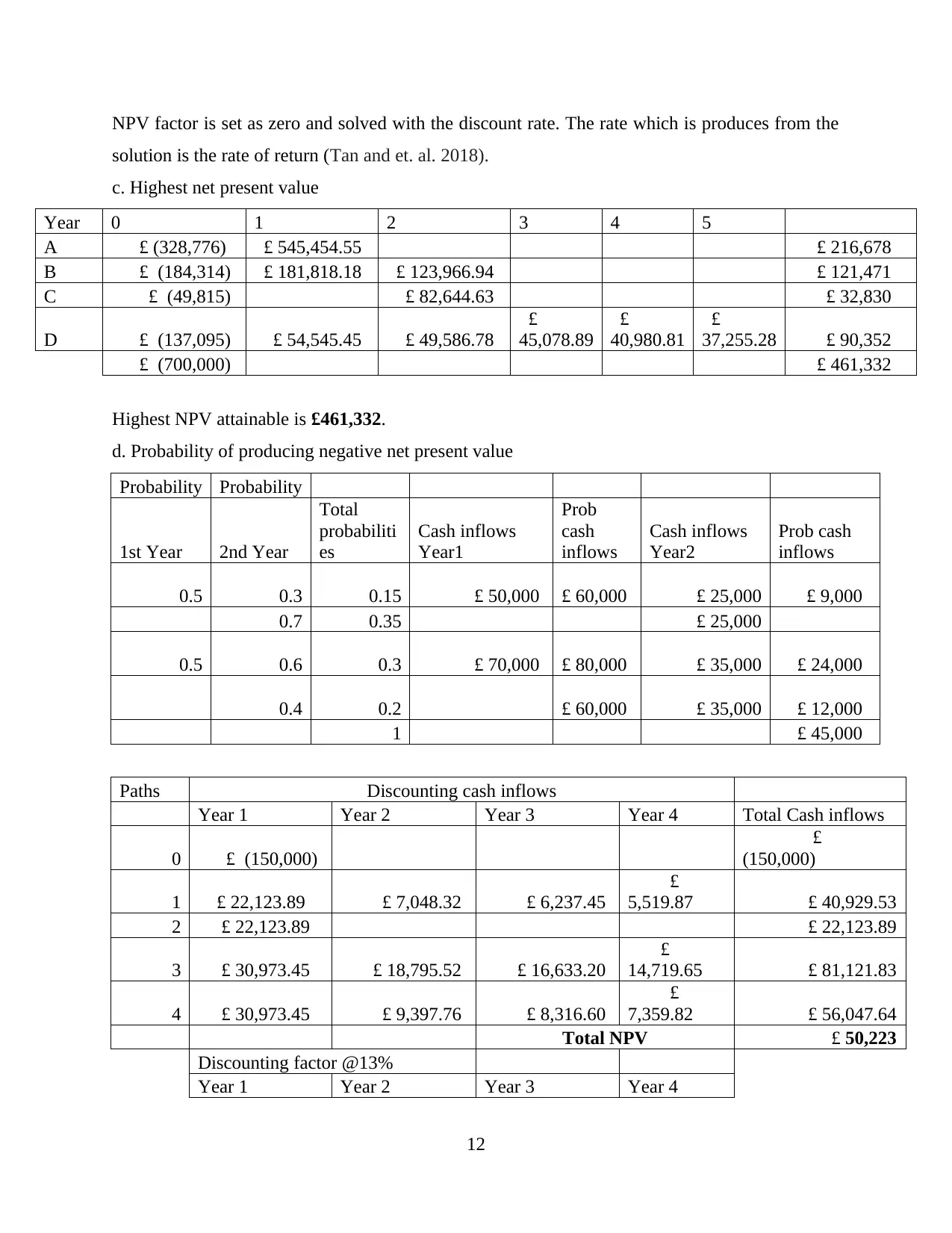
NPV factor is set as zero and solved with the discount rate. The rate which is produces from the
solution is the rate of return (Tan and et. al. 2018).
c. Highest net present value
Year 0 1 2 3 4 5
A £ (328,776) £ 545,454.55 £ 216,678
B £ (184,314) £ 181,818.18 £ 123,966.94 £ 121,471
C £ (49,815) £ 82,644.63 £ 32,830
D £ (137,095) £ 54,545.45 £ 49,586.78
£
45,078.89
£
40,980.81
£
37,255.28 £ 90,352
£ (700,000) £ 461,332
Highest NPV attainable is £461,332.
d. Probability of producing negative net present value
Probability Probability
1st Year 2nd Year
Total
probabiliti
es
Cash inflows
Year1
Prob
cash
inflows
Cash inflows
Year2
Prob cash
inflows
0.5 0.3 0.15 £ 50,000 £ 60,000 £ 25,000 £ 9,000
0.7 0.35 £ 25,000
0.5 0.6 0.3 £ 70,000 £ 80,000 £ 35,000 £ 24,000
0.4 0.2 £ 60,000 £ 35,000 £ 12,000
1 £ 45,000
Paths Discounting cash inflows
Year 1 Year 2 Year 3 Year 4 Total Cash inflows
0 £ (150,000)
£
(150,000)
1 £ 22,123.89 £ 7,048.32 £ 6,237.45
£
5,519.87 £ 40,929.53
2 £ 22,123.89 £ 22,123.89
3 £ 30,973.45 £ 18,795.52 £ 16,633.20
£
14,719.65 £ 81,121.83
4 £ 30,973.45 £ 9,397.76 £ 8,316.60
£
7,359.82 £ 56,047.64
Total NPV £ 50,223
Discounting factor @13%
Year 1 Year 2 Year 3 Year 4
12