International Standard Golf Course Modelling by Integer Programming

This case study examines the feasibility of constructing an international standard golf course, specifically focusing on the Cunningham Gudgal Golf Resort. The study employs integer programming to optimize the design, considering various constraints such as budget, acreage, and the number of different types of golf holes. The primary objective is to maximize the golfers' enjoyment index, comparing different clubhouse models: standard and exclusive. The analysis explores multiple scenarios, including variations in clubhouse costs, acreage, and overall project budgets. Findings reveal the optimal solutions for each model, highlighting the trade-offs between cost, land use, and enjoyment. The case study provides a detailed business report, discussing the implications of each model and offering recommendations for the most viable approach, ultimately aiming to provide the maximum enjoyment index within the project's financial and practical constraints. The study provides detailed solutions for the golf course design including the number of different types of holes to be built, the acreage for the clubhouse, and the overall budget for the project.

International Standard Golf Course Modelling by Integer Programming –
A Case Study on Cunningham Gudgal Golf Resort
1

Table of Contents
Part 1: Action Plan.....................................................................................................................2
Part 2: Spread Sheet Model Implementation.............................................................................3
Part 3: Business Report & Communication...............................................................................8
Executive Summary.................................................................................................................10
Overview of the Study.............................................................................................................11
Management Policy..............................................................................................................11
Mathematical Modelling......................................................................................................11
Analysis and Findings..............................................................................................................12
Model 1: Standard Clubhouse Model..................................................................................12
Model 2: Exclusive Clubhouse Model.................................................................................12
Model 3: Exclusive Clubhouse with Reduced Area............................................................13
Model 4: Exclusive Clubhouse with Reduced Cost.............................................................13
Model 5: Exclusive Clubhouse with Increased Overall Cost...............................................14
Discussion of Implications.......................................................................................................14
Recommendation......................................................................................................................15
References................................................................................................................................16
2

Part 1: Action Plan
1. There were six decision variables in the optimization problem. Number of golfing holes
to be built were the desion variables of the study. The list provided below with
abbreviation and algebric name for each variable.
Table 1: Decision Variables with abbreviation and algebraic form
Kind of golfing hole Abbreviatio
n
Algebric Expression
“Straight par 5” Sp5 X1
“Dogleg par 5” Dp5 X2
“Straight par 4” Sp4 X3
“Dogleg par 4” Dp4 X4
“long par 3” lp3 X5
“short par 3” sp3 X6
2. The objective was to maximize enjoyment index of golfers. Hence, the objective function
was the enjoyment index from golf course and clubhouse.
3. The constraints were practical, mangement oriented or technological in nature. – There
were limitations as well as requirement criterion with some restrictions.
Table 2: Constraints with limitations, requirement and restrictions
Contraint
Type
Constraint Requirement Restrictio
n
Limitation
Technical Sp5 ≥ 1
Dp5 ≥ 1
Sp4 ≥ 2
Dp4 ≥ 2
lp3 ≥ 1
sp3 ≥ 1
Sp5 & Dp5 ≤ 4
Sp4 & Dp4 ≤ 14
lp3 & sp3 ≤ 4
Total Par ≥ 70 ≤ 72
Total Golf -Holes = 18
Total acreage ≥ 36 ≤ 42
Management Standard Clubhouse Acreage = 2
Standard Clubhouse Cost = $ 3.5 Million
Overall Budget = 20 Million
Exclusive Clubhouse Acreage ≤ 4
Exclusive Clubhouse Cost ≤ $ 6 Million
3

Practical Sp5, Dp5, Sp4, Dp4, lp3, sp3 Integer
4. Mathematical modelling of the integer programming problem was stated as below.
Objective Function:
Max Z = 2X1 + 1.5 X2 + 1.5 X3 + 2X4 + 1.75 X5 + 2.25 X6 +X7
X7 = Enjoyment Index of Clubhouse (Standard = 0, Exclusive = 4)
Constraints:
Individual Pars => X1 ≥ 1, X2 ≥ 1, X3 ≥ 1, X4 ≥ 1, X5 ≥ 1, X6 ≥ 1
Sum of Pars => X1 + X2 ≥ 4, X3 + X4 ≥ 14, X5 + X6 ≥ 4
Total Par => 70 ≤ 5X1 + 5X2 + 4X3 + 4X4 + 3X5 + 3X6 ≤ 72
Total Holes => X1 + X2 + X3 + X4 + X5 + X6 = 18
Acreage: 36 ≤ 3X1 + 3.5X2 + 2X3 + 2.5 X4 + X5 + 0.75X6 + X8 ≤ 42
X8 : Clubhouse Areage (Standard = 2, Exclusive = 4)
Budget => 10,00,000 X1 + 15,00,000 X2 + 7,50,000 X3 + 9,00,000 X4 + 6,00,000 X5 +
6,50,000 X6 + X9 ≤ 2,00,00,000
X9 = Clubhouse Cost (Standard = $ 3.5 Million, Exclusive =$ 6 Million)
X1, X2, X3, X4, X5, X6 ≥ 0 (Integer), X7, X8, X9 ≥ 0 (Mason, 2012).
Part 2: Spread Sheet Model Implementation
Standard Clubhouse Model
4

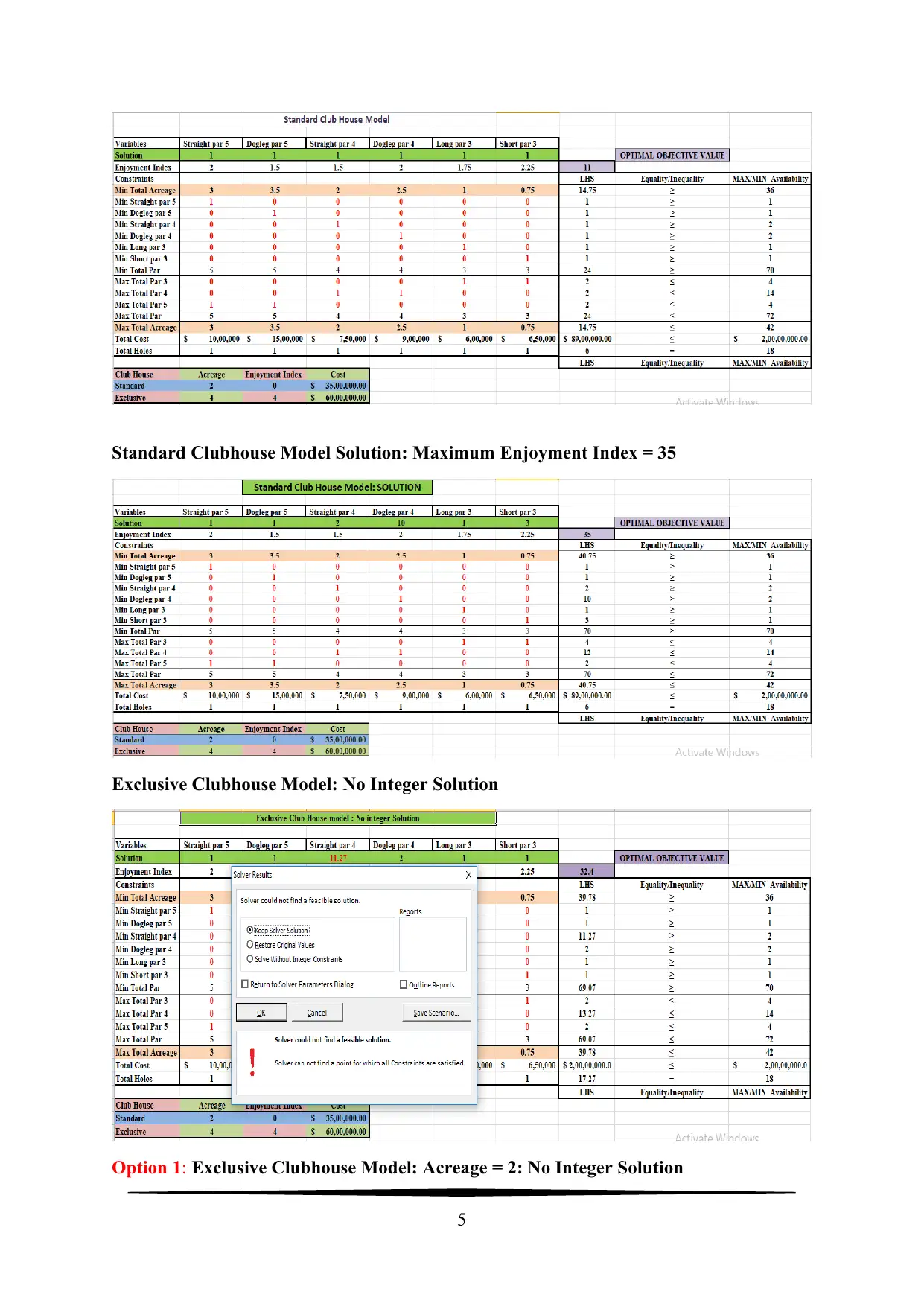
Standard Clubhouse Model Solution: Maximum Enjoyment Index = 35
Exclusive Clubhouse Model: No Integer Solution
Option 1: Exclusive Clubhouse Model: Acreage = 2: No Integer Solution
5

Exclusive Clubhouse Model: Acreage = 2.5: No Integer Solution
Exclusive Clubhouse Model: Acreage = 3: No Integer Solution
Exclusive Clubhouse Model: Acreage = 3.5: No Integer Solution
6

Option 2: Exclusive Clubhouse: Budget = $ 5.5 Million: Maximum Enjoyment Index =
35.5
Exclusive Clubhouse: Budget = $ 5 Million: Maximum Enjoyment Index = 37
Exclusive Clubhouse: Budget = $ 4 Million: Maximum Enjoyment Index = 38
7

Exclusive Clubhouse: Budget = $ 3.5 Million: Maximum Enjoyment Index = 38
Option 3: Overall Budget = $ 21.5 Million: Maximum Enjoyment Index = 38
Overall Budget = $ 22 Million: Maximum Enjoyment Index = 38
8

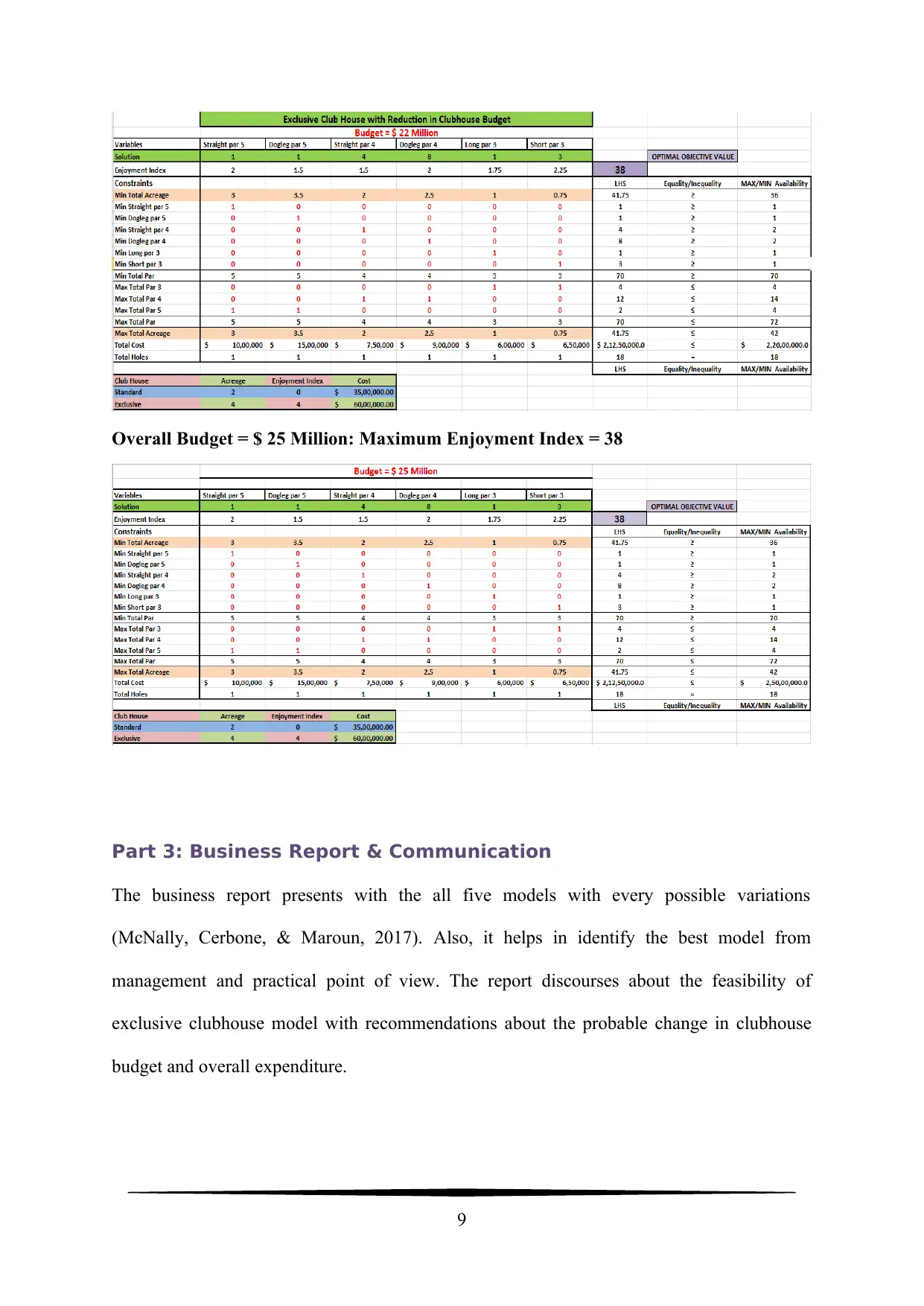
Overall Budget = $ 25 Million: Maximum Enjoyment Index = 38
Part 3: Business Report & Communication
The business report presents with the all five models with every possible variations
(McNally, Cerbone, & Maroun, 2017). Also, it helps in identify the best model from
management and practical point of view. The report discourses about the feasibility of
exclusive clubhouse model with recommendations about the probable change in clubhouse
budget and overall expenditure.
9

Feasibility of International Standard Golf Course with Exclusive Clubhouse
10

Executive Summary
The report elucidates the feasibility of construction an international standard golf-
course at Charters Towers. The proposed model by management for a golf course with a
standard clubhouse has been appraised. Parallel study on golf course with exclusive
clubhouse model has also been assessed in pursuit of best feasible model providing maximum
enjoyment to golfers. The optimization part of the mathematical problems has been estimated
using Integer Programming methodology. According to the guidelines, an international
standard golf course should have 18 golf holes with individual restrictions on each kind of
golfing holes as mentioned in the action plan. The purpose of using the Integer Programming
method was to satisfy all constraints and find integer solution for all kind of golfing holes. A
standard clubhouse model was first optimized to achieve a maximum enjoyment index (EI) of
35. The stakeholders were inclined towards higher EI with luxurious facilities in the
clubhouse. Hence, an exclusive clubhouse with international standard golf course model was
assessed, which lacked any feasible integer solution. Subsequently, the land area of exclusive
clubhouse was altered to achieve a realistic solution, only to learn that no such option existed.
The cost of the exclusive clubhouse was reduced gradually from $ 6 million to $ 3.5 million
11

(standard model clubhouse cost), and optimum solution with integer number of holes was
evaluated to provide EI of 38 (at $ 4 million budget and below). Finally, overall budget was
hypothetically raised from $ 20 million to achieve EI of 38 at $ 21.5 million. Further increase
in budget did not confirm any further increase in EI.
Overview of the Study
Management Policy
The golf course project was a transcendent project of Cunningham Holdings Limited
(CHL) towards eco-friendly and sustainable project, planned for rural development (Addanki,
& Venkataraman, 2017). The business perspective of the company was to build world class
sustainable service driven by premium leadership skills that will heighten the brand value of
CHL. Accentuate of the golf course project was in boosting the neighbouring economy by
promoting tourism in a tropical area like Charters Towers. The objective of the management
was to build an international standard golf course with consisting of a standard clubhouse
within a budget of $ 20 million. An exclusive clubhouse model on 4 acreage land with an EI
of 4, and cost of $ 6 million for the clubhouse was later introduced due to demand from the
shareholders.
Mathematical Modelling
The standard clubhouse model with 18 holes golf course was outlined by linear
programming technique with integer constraints on decision variables (Vielma, 2015). The
decision variables of the study were the number of six types of golfing holes (Sp5, Dp5, Sp4,
Dp4, lp3, and sp3). Each type of golfing hole had enjoyment index associated with it, where
standard clubhouse had zero EI. The objective of the model was to maximize the total EI with
constraints of international guidelines for the golf course. Another mathematical model for
the exclusive clubhouse was constructed altering the acreage, cost, and EI of the clubhouse.
12