Investment Management Report: Bond Pricing, Yields, and Risk Analysis

This report delves into the core concepts of investment management, focusing on bond pricing, yield curve analysis, and interest rate risk. It begins with an introduction to investment decisions and capital budgeting, emphasizing the significance of short-term asset investments. The report then analyzes the reasons behind the Reserve Bank of Australia's (RBA) cash rate decrease in June 2019, exploring its impact on the economy. It includes detailed calculations and tables for bond pricing, yield to maturity, and zero-coupon yields. The report also examines the trading of zero-coupon bonds and the application of arbitrage pricing theory. Furthermore, it explores the use of yield curves in forecasting, the theory of liquidity preference, and the impact of interest rate changes on investment strategies, offering insights for Roosters Bond Trust to manage risk effectively. The report concludes with an analysis of bond duration and convexity, providing a framework for immunizing portfolio risk.

Investment
Management

Table of Contents
INTRODUCTION ..........................................................................................................................3
Question. 1.......................................................................................................................................3
Question 2........................................................................................................................................8
Question 3......................................................................................................................................12
CONCLUSION..............................................................................................................................16
References .....................................................................................................................................17

INTRODUCTION
In present business world, Decision taken by shareholders and senior executives
regarding the number of monetary resources deployed in useful investment opportunities is
known as investment decision (Adekola and Sergi, 2016). Longer-term capital investment
strategy is defined as Capital Budgeting. It is a method of choosing the asset or a plan for a
project which will generate long-term profits. Making investment decision related to short term
assets is also significant for an organisation because it support in obtaining regular profit which
is beneficial for long term success. It aid company to keep actual investment in goods, programs,
machinery and technology that support to reach the desired results. This also takes into
consideration depreciation spending for an organisation in long run. This is the method of
preserving which support to keep established services and products available for real consumer
or stakeholder.
In this project, concepts and calculation for pricing bond and mispricing, forward Yields
and Holding Period Returns are discussed. In addition report also defines the concepts of Interest
Rate Risk which would help roosters bond trust to provides meaningful advice to several groups
of investors relating to manage the risk they are exposed to when interest rates change.
Question. 1
(A). Reasons for decreased in cash rate in June 2019 by RBA
The Reserve Bank of Australia define the cash rate target for a specific period which is
consider to be market interest rate overnight funding (Reason for decreased cash rate, 2019).
The RBA uses it as a monetary planning tool and controls the cash rate across its activities upon
financial market. In respective meeting Broad of RBA decided to reduce the cash rate by 0.25%
points equals to new low rate of 1% that mainly reflect a high concern to slow economy. There
are some reasons due to which the decision of cut down in cash rate have been made by RBS
which are discussed below:
Outlook for the global economy remains reasonable: It have been observed that,
investment is influenced by the uncertainties created by trading and technological conflicts and
the threats to world economy are skewed downwards. Inflation continues to decline in certain
developed economies, unemployment rates considered to be low and productivity growth has
risen.

Global financial conditions remain accommodative: The continued potential risks for
global economy leading to low inflation that have contributed to assumptions that global central
banks would loosen monetary and fiscal policy. Lengthy-term treasury bond rates in a variety of
countries, like within Australia, have fallen significantly at are recorded as the lowest. Bank
bond yields have already decreased in Australia, to money market premiums having totally
reversed from last year's increases (Balaman, 2016).
The announcement today related with lower the cash rate would contribute in making
further advances within economy's excess capacity. This will allow better progress for improving
the economy and more confident movement upwards to the goal of inflation.
(B). Twenty Treasury Bonds and twenty zero-coupon yields (ZCY).
(I).
Code Maturity (years) Face value Coupon (p.a.) coupons Bond Price
GSBG20 0.5 100 5.25% $2.63 102.1168
GSBU20 1.0 100 2.50% $1.25 101.5863
GSBI21 1.5 100 5.75% $2.88 107.2873
GSBW21 2.0 100 2.00% $1.00 102.3857
GSBM22 2.5 100 5.75% $2.88 112.1934
GSBU22 3.0 100 2.25% $1.13 104.2046
GSBG23 3.5 100 5.50% $2.75 115.9013
GSBG24 4.0 100 2.75% $1.38 107.1362
GSBG25 4.5 100 3.25% $1.63 110.1021
GSBG26 5.0 100 5.25% $2.63 120.8336
GSBG27 5.5 100 5.75% $2.88 125.3308
GSBU27 6.0 100 1.75% $0.88 104.0564
GSBI28 6.5 100 2.25% $1.13 107.2938
GSBN28 7.0 100 1.50% $0.75 102.5223
GSBG29 7.5 100 3.25% $1.63 115.0504

GSBU31 8.0 100 1.50% $0.75 102.3238
GSBG33 8.5 100 3.25% $1.63 116.3784
GSBK35 9.0 100 2.75% $1.38 112.7113
GSBK37 9.5 100 1.50% $0.75 101.9507
GSBK39 10.0 100 2.75% $1.38 113.5748
(ii).
Code
Maturity
(years) Face value
Coupon
(p.a.) coupons PV Yield to maturity
GSBG20 0.5 100 5.25% $2.63 102.1168 0.9953%
GSBU20 1.0 100 2.50% $1.25 101.5863 0.9029%
GSBI21 1.5 100 5.75% $2.88 107.2873 0.8504%
GSBW21 2.0 100 2.00% $1.00 102.3857 0.7953%
GSBM22 2.5 100 5.75% $2.88 112.1934 0.8130%
GSBU22 3.0 100 2.25% $1.13 104.2046 0.8281%
GSBG23 3.5 100 5.50% $2.75 115.9013 0.8768%
GSBG24 4.0 100 2.75% $1.38 107.1362 0.9285%
GSBG25 4.5 100 3.25% $1.63 110.1021 0.9514%
GSBG26 5.0 100 5.25% $2.63 120.8336 0.9712%
GSBG27 5.5 100 5.75% $2.88 125.3308 1.0045%
GSBU27 6.0 100 1.75% $0.88 104.0564 1.0506%
GSBI28 6.5 100 2.25% $1.13 107.2938 1.0848%
GSBN28 7.0 100 1.50% $0.75 102.5223 1.1243%
GSBG29 7.5 100 3.25% $1.63 115.0504 1.1498%
GSBU31 8.0 100 1.50% $0.75 102.3238 1.1946%

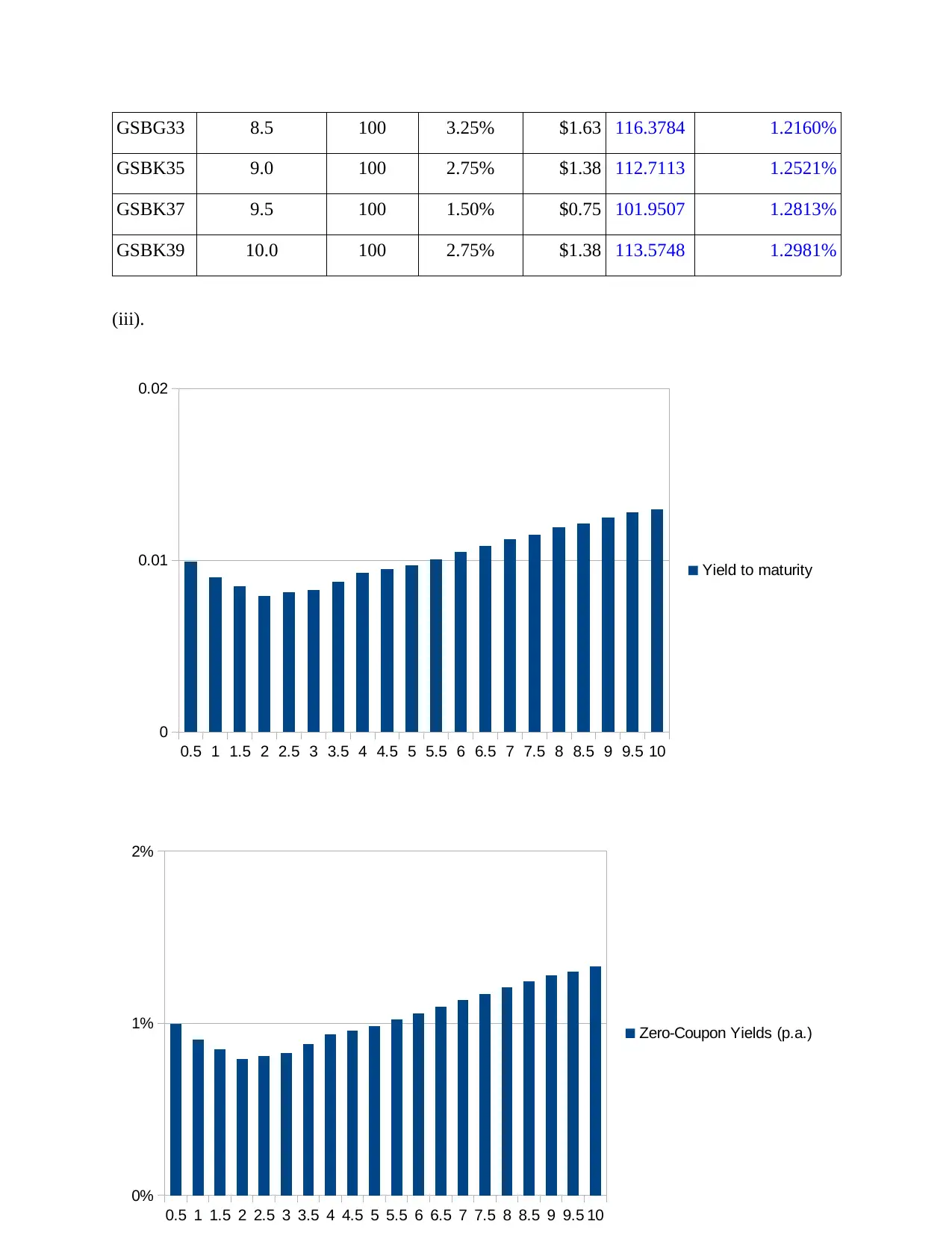
GSBG33 8.5 100 3.25% $1.63 116.3784 1.2160%
GSBK35 9.0 100 2.75% $1.38 112.7113 1.2521%
GSBK37 9.5 100 1.50% $0.75 101.9507 1.2813%
GSBK39 10.0 100 2.75% $1.38 113.5748 1.2981%
(iii).
0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
0
0.01
0.02
Yield to maturity
0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10
0%
1%
2%
Zero-Coupon Yields (p.a.)

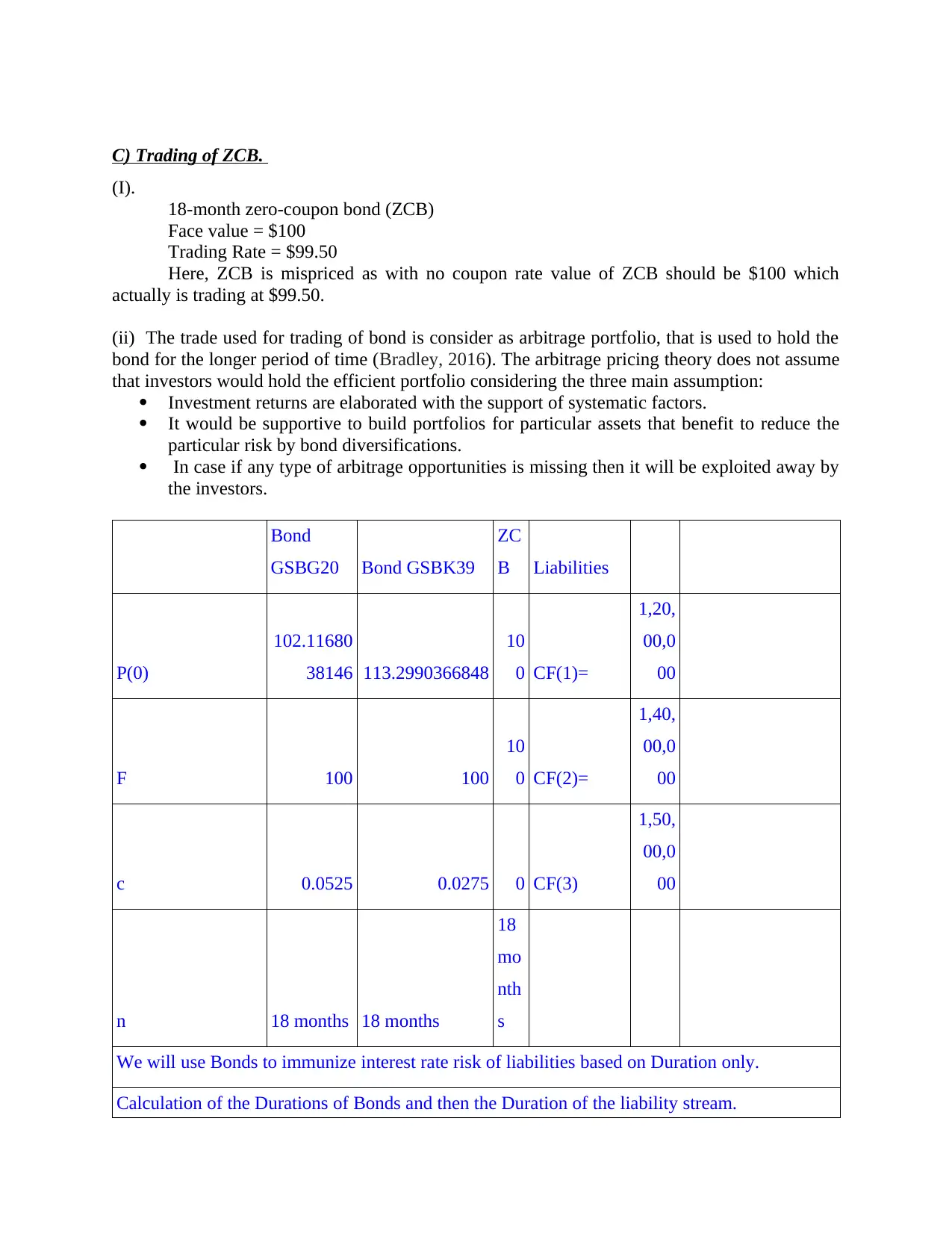
C) Trading of ZCB.
(I).
18-month zero-coupon bond (ZCB)
Face value = $100
Trading Rate = $99.50
Here, ZCB is mispriced as with no coupon rate value of ZCB should be $100 which
actually is trading at $99.50.
(ii) The trade used for trading of bond is consider as arbitrage portfolio, that is used to hold the
bond for the longer period of time (Bradley, 2016). The arbitrage pricing theory does not assume
that investors would hold the efficient portfolio considering the three main assumption:
 Investment returns are elaborated with the support of systematic factors.
 It would be supportive to build portfolios for particular assets that benefit to reduce the
particular risk by bond diversifications.
 In case if any type of arbitrage opportunities is missing then it will be exploited away by
the investors.
Bond
GSBG20 Bond GSBK39
ZC
B Liabilities
P(0)
102.11680
38146 113.2990366848
10
0 CF(1)=
1,20,
00,0
00
F 100 100
10
0 CF(2)=
1,40,
00,0
00
c 0.0525 0.0275 0 CF(3)
1,50,
00,0
00
n 18 months 18 months
18
mo
nth
s
We will use Bonds to immunize interest rate risk of liabilities based on Duration only.
Calculation of the Durations of Bonds and then the Duration of the liability stream.

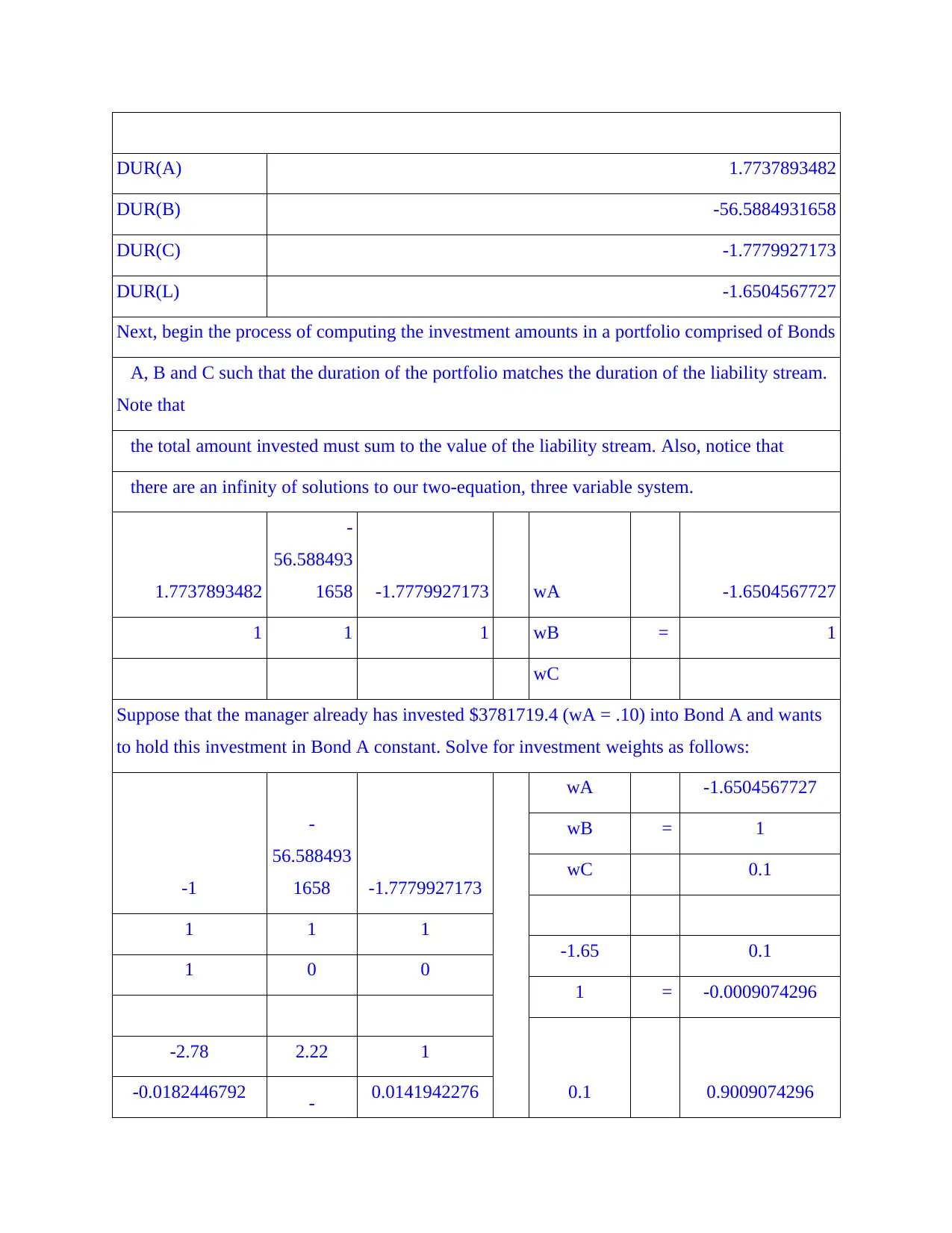
DUR(A) 1.7737893482
DUR(B) -56.5884931658
DUR(C) -1.7779927173
DUR(L) -1.6504567727
Next, begin the process of computing the investment amounts in a portfolio comprised of Bonds
A, B and C such that the duration of the portfolio matches the duration of the liability stream.
Note that
the total amount invested must sum to the value of the liability stream. Also, notice that
there are an infinity of solutions to our two-equation, three variable system.
1.7737893482
-
56.588493
1658 -1.7779927173 wA -1.6504567727
1 1 1 wB = 1
wC
Suppose that the manager already has invested $3781719.4 (wA = .10) into Bond A and wants
to hold this investment in Bond A constant. Solve for investment weights as follows:
-1
-
56.588493
1658 -1.7779927173
wA -1.6504567727
wB = 1
wC 0.1
1 1 1
-1.65 0.1
1 0 0
1 = -0.0009074296
0.1 0.9009074296
-2.78 2.22 1
-0.0182446792 - 0.0141942276

0.0324389
068
0.0182446792
1.0324389
068 -1.0141942276
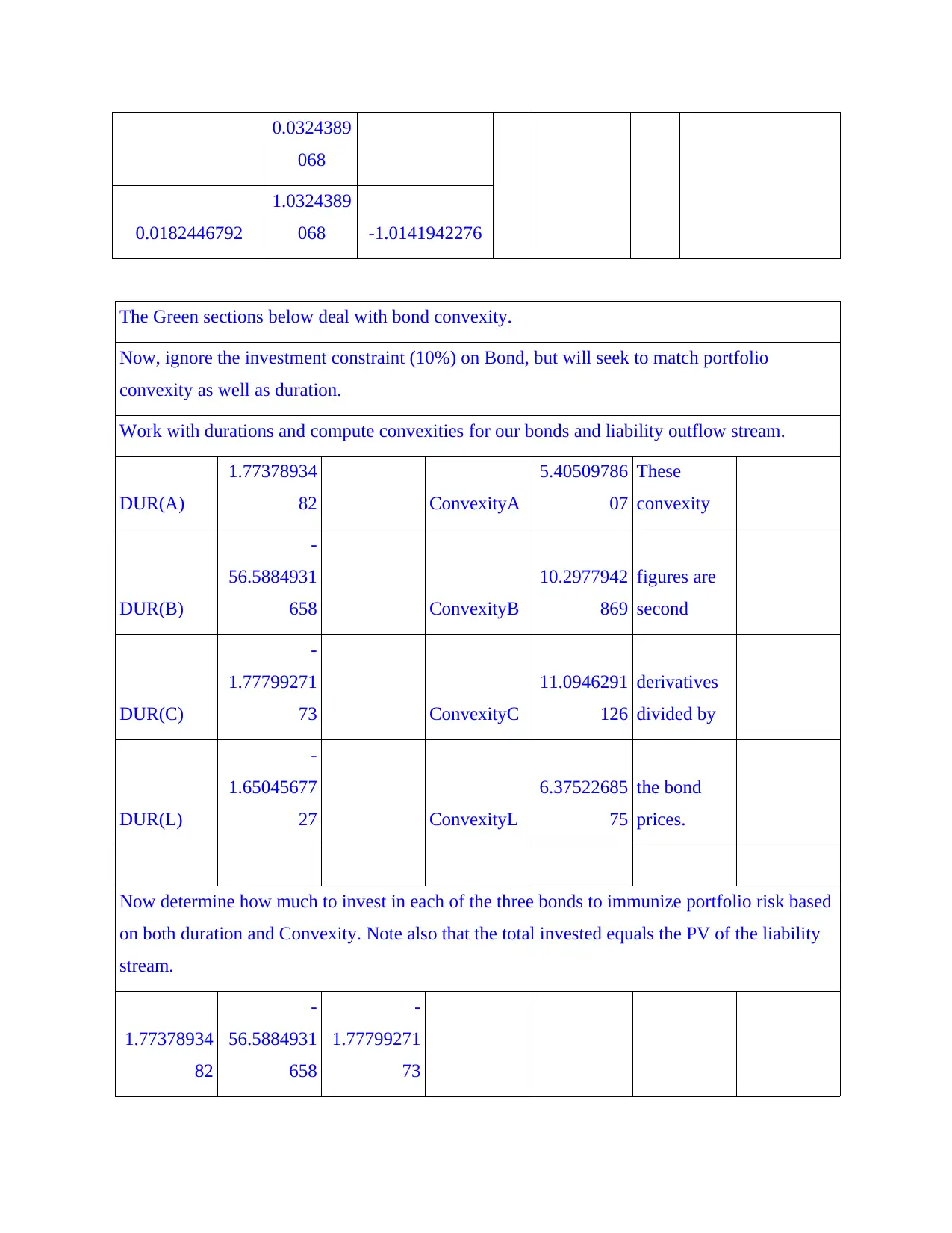
The Green sections below deal with bond convexity.
Now, ignore the investment constraint (10%) on Bond, but will seek to match portfolio
convexity as well as duration.
Work with durations and compute convexities for our bonds and liability outflow stream.
DUR(A)
1.77378934
82 ConvexityA
5.40509786
07
These
convexity
DUR(B)
-
56.5884931
658 ConvexityB
10.2977942
869
figures are
second
DUR(C)
-
1.77799271
73 ConvexityC
11.0946291
126
derivatives
divided by
DUR(L)
-
1.65045677
27 ConvexityL
6.37522685
75
the bond
prices.
Now determine how much to invest in each of the three bonds to immunize portfolio risk based
on both duration and Convexity. Note also that the total invested equals the PV of the liability
stream.
1.77378934
82
-
56.5884931
658
-
1.77799271
73

1 1 1
5.40509786
07
10.2977942
869
11.0946291
126
0.00253223
7
1.93697160
82
-
0.17418061
38
-
1.65045677
27
0.82235133
3
= the fractional amount to
invest in Bond A.
-
0.01808058
74
0.09307903
16
-
0.01128709
96 1
0.05096243
87
= the fractional amount to
invest in Bond B.
0.01554835
04
-
1.03005063
97
0.18546771
35
6.37522685
75
0.12668622
83
= the fractional amount to
invest in Bond C.

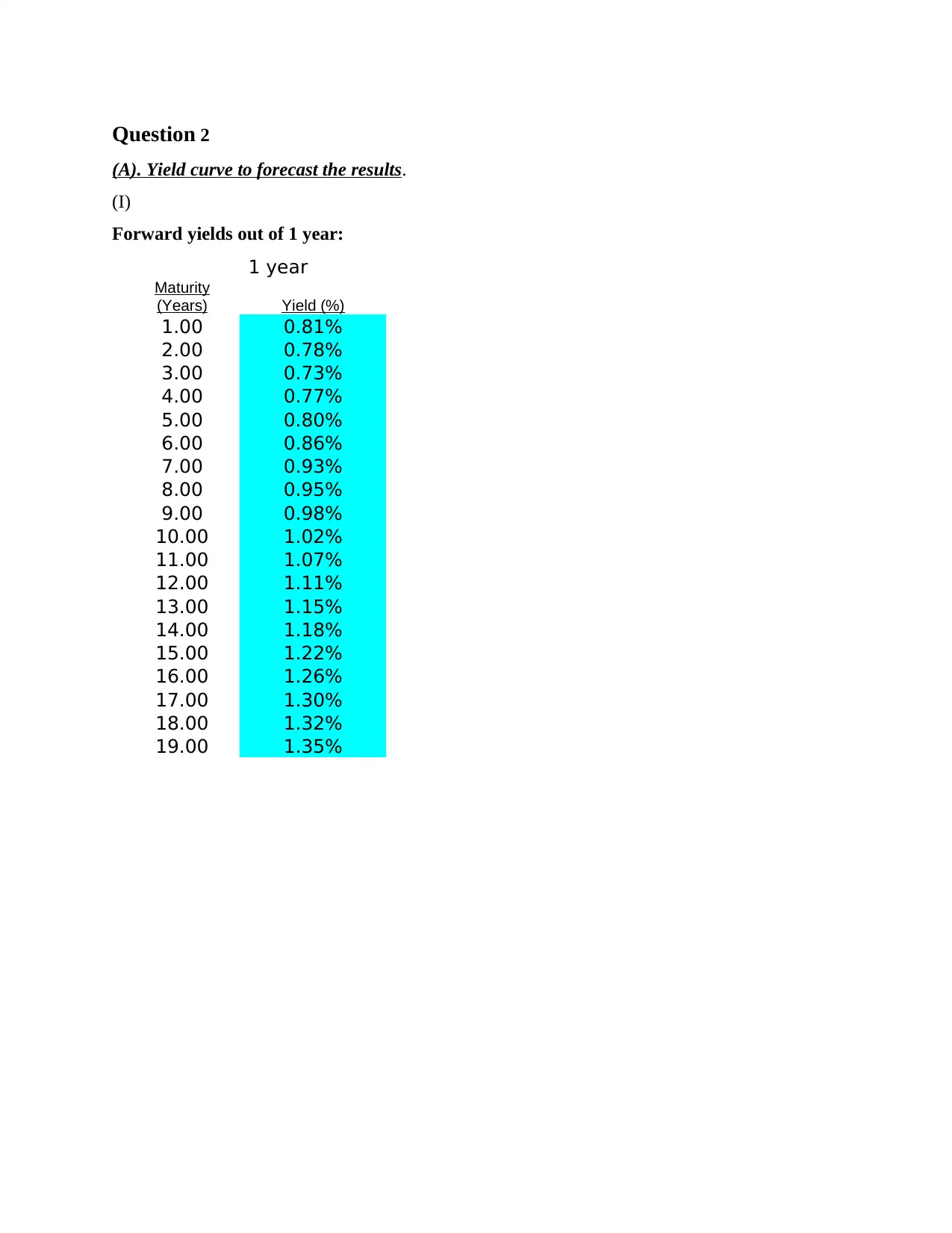
Question 2
(A). Yield curve to forecast the results.
(I)
Forward yields out of 1 year:
1 year
Maturity
(Years) Yield (%)
1.00 0.81%
2.00 0.78%
3.00 0.73%
4.00 0.77%
5.00 0.80%
6.00 0.86%
7.00 0.93%
8.00 0.95%
9.00 0.98%
10.00 1.02%
11.00 1.07%
12.00 1.11%
13.00 1.15%
14.00 1.18%
15.00 1.22%
16.00 1.26%
17.00 1.30%
18.00 1.32%
19.00 1.35%

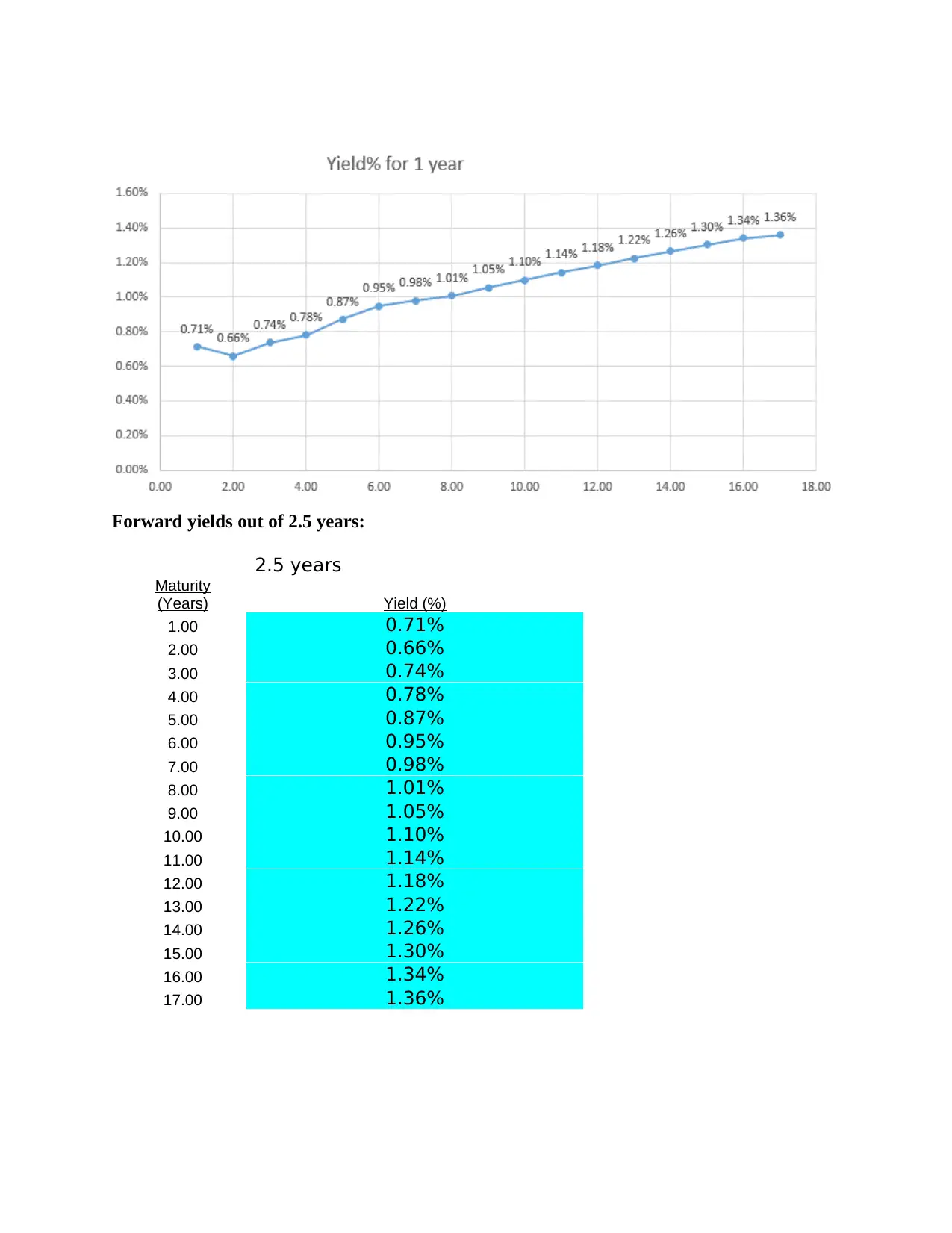
Forward yields out of 2.5 years:
2.5 years
Maturity
(Years) Yield (%)
1.00 0.71%
2.00 0.66%
3.00 0.74%
4.00 0.78%
5.00 0.87%
6.00 0.95%
7.00 0.98%
8.00 1.01%
9.00 1.05%
10.00 1.10%
11.00 1.14%
12.00 1.18%
13.00 1.22%
14.00 1.26%
15.00 1.30%
16.00 1.34%
17.00 1.36%

(ii)
The theory of liquidity preference implies that individual who make investment in bonds
and securities seeks a higher rate of return or yield on long-term bonds that offer higher risk as
investment maker want cash or any other highly liquid investments, with all other variables
being equivalent. Investments which are more liquid are, as per this principle, simpler to cash in
for full value. Money is perhaps most liquid asset widely accepted. As per liquidity preference
theory short-period securities interests rate is much lower as investors do not lose liquidity for
extended periods than moderate or long-term bonds.
Theory of liquidity preference indicates that investors are steadily demanding better
yields on mid and long-term bonds relative to short-term bonds. Roosters Bond Trust can easily
forecast future interest rates by applying information as stated in curves by matching implied
forecasted yield of 1 year and 2.5 years.
(B). Impact of changes in the trading yield for respective investment
In modern era of business, Holding Period return is described as the actual total return
that have been received from the holding on an investment or bond or specific portfolio within a
specific period of time which is known as holding period that is denoted by percentage (Briston,
2017). Yield on holding periods is computed on the justification of complete investment or
valuation performance. Equating returns between securities retained over various periods is
especially useful. Therefore, it is stated that amount in holding period for a specific time is
referred as the investment that is held by an investor, or the period between the sales and
purchase of a security.
(I).

Code Maturity (years) Face value
Coupon
(p.a.) coupons Bond Price
Yield to
maturity
GSBU31 8.0 100 1.50% $0.75 $102.24 1.1946%
4.5 100 1.50% $0.75 $101.337 0.9514%
HPR = [(0.75) + (0.75 * .9514%) + (102.24-101.337)]/ 102.24 = 1.62376%
(ii).
Cases:
(a). YTM that is higher by 10 basis points
HPR = [(0.75) + (0.75 * 1.0514%) + (102.24-101.337)]/ 102.24 = 1.6244967723%
(b). YTM that is higher by 50 basis points
HPR = [(0.75) + (0.75 * 1.4514%) + (102.24-101.337)]/ 102.24 = 1.6274310446%
(c). YTM that is higher by 75 basis points than yield would be 1.49%
HPR = [(0.75) + (0.75 * 1.7014%) + (102.24-101.337)]/ 102.24 = 1.6292649648%
(iii).
(a). YTM that is lower by 10 basis points than yield would be .64%
HPR = [(0.75) + (0.75 * .8514%) + (102.24-101.337)]/ 102.24 = 1.6230296362%
(b). YTM that is lower by 50 basis points than yield would be .24%
HPR = [(0.75) + (0.75 * .4514%) + (102.24-101.337)]/ 102.24 = 1.6200953638%
(c). YTM that is lower by 75 basis points than yield would be nil
HPR = [(0.75) + (0.75 * .2014%) + (102.24-101.337)]/ 102.24 = 1.6182614437%
(iv).
If the coupons received during the investment period are reinvested at the bond’s current YTM:
(a). YTM that is higher by 10 basis points than yield would be .84%
HPR = [(1.0514) + ( 1.0514 * 1.0514%) + (102.24-101.337)]/ 102.24 = 1.9223928204%
(b). YTM that is higher by 50 basis points than yield would be 1.24%
HPR = [(1.4514) + ( 1.4514 * 1.4514%) + (102.24-101.337)]/ 102.24 = 2.3234209894%
(c). YTM that is higher by 75 basis points than yield would be 1.49%
HPR = [(1.7014) + ( 1.7014 * 1.7014%) + (102.24-101.337)]/ 102.24 = 2.5756529926%
(v).

If the coupons received during the investment period are reinvested at the bond’s current
YTM:
(a). YTM that is lower by 10 basis points
HPR = [(0.8514) + (0.8514 * .8514%) + (102.24-101.337)]/ 102.24 = 1.7230524448%
(b). YTM that is lower by 50 basis points
HPR = [(0.4514) + (0.4514 * .4514%) + (102.24-101.337)]/ 102.24 = 1.3267191115%
(c). YTM that is lower by 75 basis points
HPR = [(0.2014) + (0.2014 * .2014%) + (102.24-101.337)]/ 102.24 = 1.0806001757%
(vi). Relationship between the YTMs and HPR as shown in (i) to (v)
From above calculations of HPR in different case of YTMs it has been analysed that with
increase in YTMs, HPR has been also increased. YTM represents the return an investor earns for
retaining a bond till it reaches maturity. This does not consider investor's taxes or costs of
dealing accrued. Bond holders are not required to hold bond of an issuer till maturity. The return
on bond or property during holding period is referred to as return on holding period (HPR). Thus
with increase and decrease in YTM, HPR also increases and decreases simultaneously (Chandra,
2017).
Question 3
A) Recommendation to Storm Investors
The current changes in interest rate by reserve bank of Australia is due to slow down in
economy that affect business and job growth within specific period. As few investors have
borrowed a certain amount of about $3,250,000 which is needed to be paid back in 3 ½ year.
Therefore they are worried about the exposure of this liability and wants to make some
meaningful investment where they can reduce the impact of changing interest rate. Rooster bond
trust have suggested to investors that they can reduce the exposure by making investment within
specific bond portfolio that contain two treasury bond that have a equal certified time period like
as liability (Sandström, Kyläheiko and Collan, 2016). This is refereed to be important and
helpful investment option, because the interest revenue is deducted from the purchase price of
bond and the respective investor are expected to obtain the entire face worth of the bonds at the
time of maturity. A balanced portfolio of bonds can produce good returns with lower inflation as
compared to equities and higher incomes than money market funds including banking securities.
Increased diversifying of treasury bond can provide stronger threat-adjusted yields for

investment firms than smaller focused portfolios. Therefore, revenue from treasury bond are tax-
free at all level within country Although tax considerations has never been the primary reason for
choosing a bond, particularly for shareholders in lower tax brackets.
B). Calculate the present value and modified duration of the liability
GSBG20 GSBU20 GSBI21 GSBW21
Coupon 5.25% Coupon 2.50% Coupon 5.75% Coupon 2.00%
Face value 100 Face value 100 Face value 100 Face value 100
Frequency 1 Frequency 1 Frequency 1.5 Frequency 2
Maturity 0.5 Maturity 1 Maturity 1.5 Maturity 2
Yield 0.9953% Yield 0.9029% Yield 0.8504% Yield 0.7953%
Price 102.112 Price 101.583 Price 107.282 Price 102.386
Macaulay
Dur 1.791
Macaulay
Dur 2.351
Macaulay
Dur 3.800
Macaulay
Dur 1.971
Modified
Dur 1.774
Modified
Dur 2.330
Modified
Dur 3.779
Modified
Dur 1.963
Dollar Dur 1.811 Dollar Dur 2.367 Dollar Dur 4.054 Dollar Dur 2.010
GSBM22 GSBU22 GSBG23 GSBG24
Coupon 5.75% Coupon 2.25% Coupon 5.50% Coupon 2.75%
Face value 100 Face value 100 Face value 100 Face value 100
Frequency 2.5 Frequency 3 Frequency 3.5 Frequency 4
Maturity 2.5 Maturity 3 Maturity 3.5 Maturity 4
Yield 0.8130% Yield 0.8281% Yield 0.8768% Yield 0.9285%
Price 112.198 Price 104.207 Price 115.916 Price 107.144
Macaulay -1.494 Macaulay -0.901 Macaulay -10.540 Macaulay -6.844

Dur Dur Dur Dur
Modified
Dur -1.489
Modified
Dur -0.898
Modified
Dur -10.514
Modified
Dur -6.829
Dollar Dur -1.671 Dollar Dur -0.936 Dollar Dur -12.187 Dollar Dur -7.316
GSBG25 GSBG26 GSBG27 GSBU27
Coupon 3.25% Coupon 5.25% Coupon 5.75% Coupon 1.75%
Face value 100 Face value 100 Face value 100 Face value 100
Frequency 4.5 Frequency 5 Frequency 5.5 Frequency 6
Maturity 4.5 Maturity 5 Maturity 5.5 Maturity 6
Yield 0.9514% Yield 0.9712% Yield 1.0045% Yield 1.0506%
Price 110.115 Price 120.863 Price 125.370 Price 104.063
Macaulay
Dur -12.499
Macaulay
Dur -27.468
Macaulay
Dur -36.745
Macaulay
Dur -12.324
Modified
Dur -12.473
Modified
Dur -27.415
Modified
Dur -36.678
Modified
Dur -12.302
Dollar Dur -13.735 Dollar Dur -33.135 Dollar Dur -45.983 Dollar Dur -12.802
GSBI28 GSBN28 GSBG29 GSBU31
Coupon 2.25% Coupon 1.50% Coupon 3.25% Coupon 1.50%
Face value 100 Face value 100 Face value 100 Face value 100
Frequency 6.5 Frequency 7 Frequency 7.5 Frequency 8
Maturity 6.5 Maturity 7 Maturity 7.5 Maturity 4.5
Yield 1.0848% Yield 1.1243% Yield 1.1498% Yield 1.1946%
Price 107.307 Price 102.527 Price 115.080 Price 101.337
Macaulay -20.268 Macaulay -14.392 Macaulay -39.734 Macaulay -11.496

Dur Dur Dur Dur
Modified
Dur -20.234
Modified
Dur -14.369
Modified
Dur -39.673
Modified
Dur -11.479
Dollar Dur -21.712 Dollar Dur -14.732 Dollar Dur -45.656 Dollar Dur -11.632
GSBG33 GSBK35 GSBK37 GSBK39
Coupon 3.25% Coupon 2.75% Coupon 1.50% Coupon 2.75%
Face value 100 Face value 100 Face value 100 Face value 100
Frequency 8.5 Frequency 9 Frequency 9.5 Frequency 10
Maturity 8.5 Maturity 9 Maturity 9.5 Maturity 10
Yield 1.2160% Yield 1.2521% Yield 1.2813% Yield 1.2981%
Price 116.414 Price 112.741 Price 101.955 Price 113.608
Macaulay
Dur -49.660
Macaulay
Dur -46.769
Macaulay
Dur -27.351
Macaulay
Dur -56.662
Modified
Dur -49.589
Modified
Dur -46.704
Modified
Dur -27.314
Modified
Dur -56.588
Dollar Dur -57.729 Dollar Dur -52.655 Dollar Dur -27.848 Dollar Dur -64.289
C). Selection of two Treasury bonds
i)
The two Treasury bond that have been selected from bond portfolio hedging that Storm
Investors should include in the bond portfolio are GSBG20 and GSBK39. The main reason for
selecting these bonds is that in context of GSBG20 the maturity time is 0.5 year at a rate of 5.25
% which would be profitable enough for Storm group to get the successive return within such a
shorter period of time. On the other side, in context of GSBK39 the maturity year is 10 and the
coupon rate of is 2.75 % that define that investor would get enough return on following
investment in longer period (Sweeting, 2017).
ii)

1. GSBK39
Coupon 2.75%
Face value 100
Frequency 10
Maturity 10
Yield 1.2981%
Price 113.608
Macaulay Duration -56.662
Modified Duration -56.588
Dollar Duration -64.289
2. GSBG20
Coupon 5.25%
Face value 100
Frequency 1
Maturity 0.5
Yield 0.9953%
Price 102.112
Macaulay Duration 1.791
Modified Duration 1.774
Dollar Duration 1.811
D) Change in interest rates will affect the present value of the liability.
(i).