Solving Knapsack Problem Using Genetic Algorithm: Discrete Structure

This assignment details the solution of the binary knapsack problem using a genetic algorithm implemented in Excel. The evolutionary algorithm, a type of genetic algorithm, is employed with specific parameters: a candidate pool size between 10 and 15, with candidates removed and added based on pool size. The algorithm iterates up to 6 times, generating 24 sub-problems. The problem is framed as maximizing the value of selected items subject to a knapsack capacity constraint (B = 30, 50, or 40 for instances 1, 2, and 3, respectively). The solution includes answer reports and population reports for each instance, showing the final item selection, objective function values, constraint satisfaction, and the mean, standard deviation, and range of item selection values across iterations. The analysis demonstrates the feasibility of the solutions within the given constraints, though the solutions are not complete due to the limited number of sub-problems evaluated. The assignment successfully uses the evolutionary algorithm of excel to find the binary solution for each instance.

Running head: DISCRETE STRUCTURE
DISCRETE STRUCTURE
Name of the Student
Name of the University
Author Note

Introduction to Knapsack problem by using the Genetic Algorithm:
In this assignment the binary knapsack problem is solved using the genetic algorithm with
excel. For computational improvement the evolutionary algorithm (a type of genetic
algorithm) of excel is chosen with specified parameters as given below.
1) The size of the pool or the total number of candidates will lie in between 10 and 15.
2) Five candidates are removed when the size of candidates reaches 15. 1 mutant solution is
added when the size of the pool is reduced from 15 to 10. A pair of parents is selected when
pool size is 11 and 13 and adding their children to the pool.
3) Iteration stops when total number of children or sub problems generated is 24 or 6
iterations are completed.
This above conditions are specified in Evolutionary algorithm specification in excel.
Total sub problems = 24
Iterations = 6
Random number seed = 0
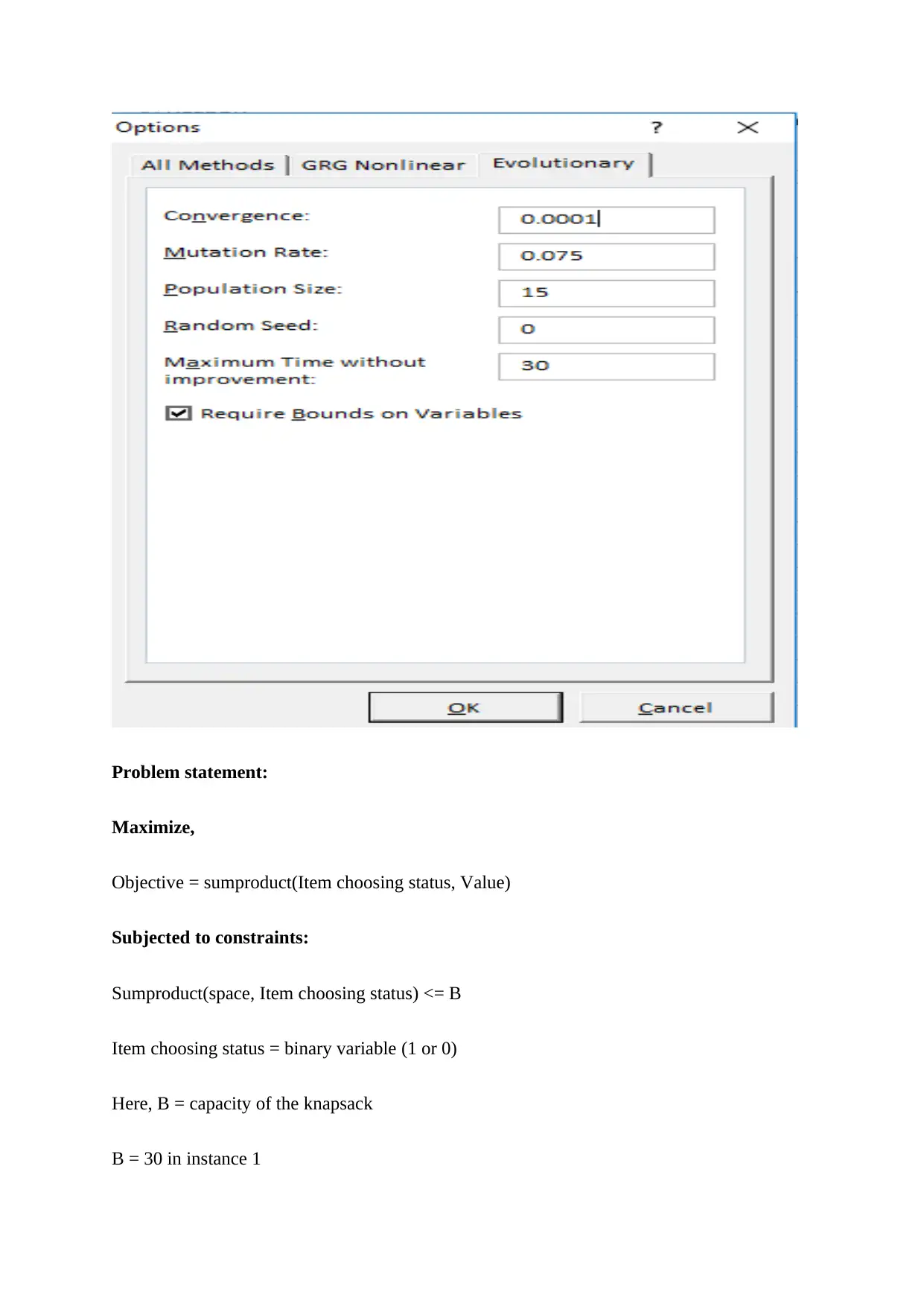
Mutation rate = 0.075
Integer tolerance = 1%
Solution precision = 0.000001
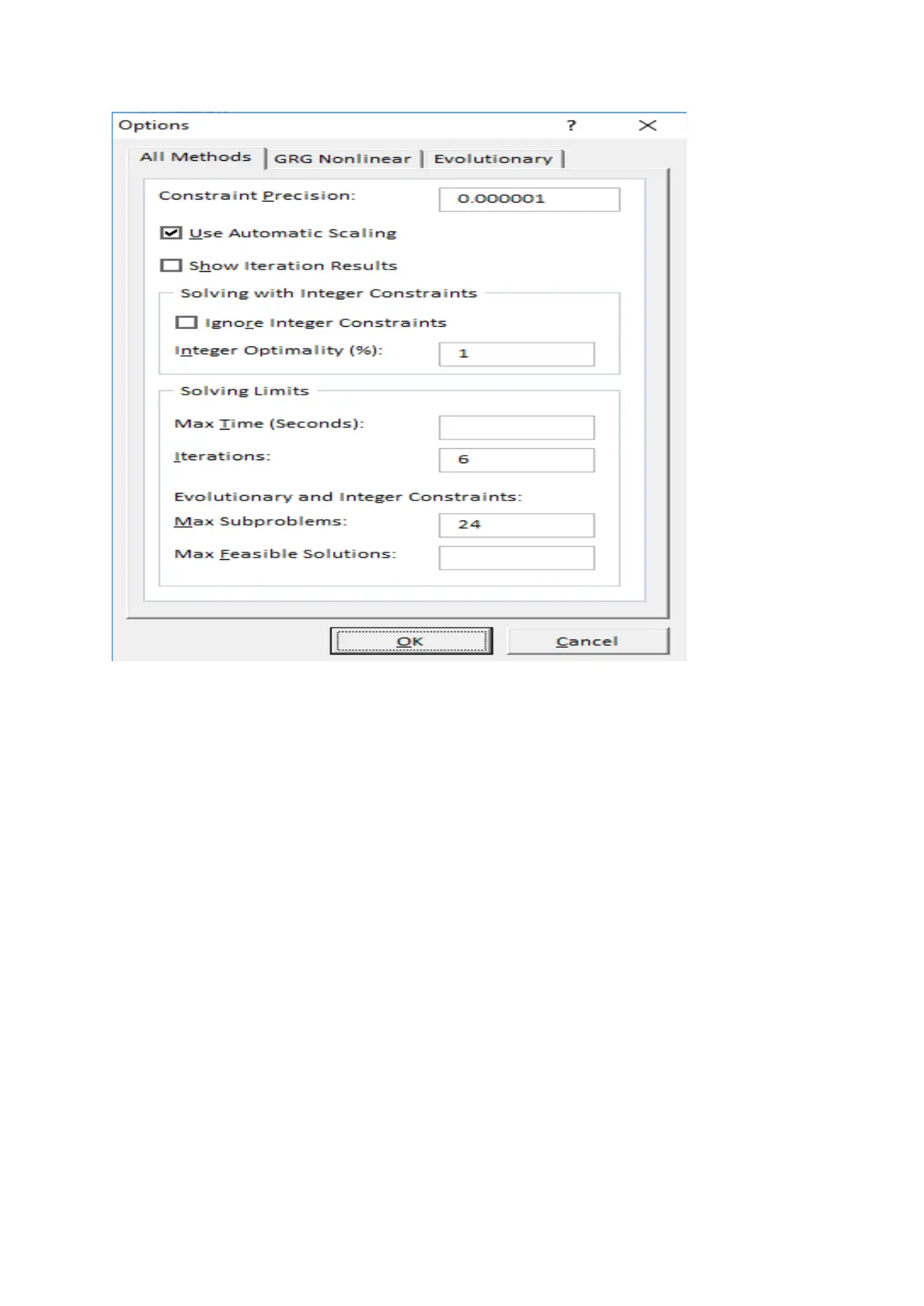
In excel solver options of Evolutionary algorithm the above are specified as given below.

Problem statement:
Maximize,
Objective = sumproduct(Item choosing status, Value)
Subjected to constraints:
Sumproduct(space, Item choosing status) <= B
Item choosing status = binary variable (1 or 0)
Here, B = capacity of the knapsack
B = 30 in instance 1

B = 50 in instance 2
B = 40 in instance 3
Solution by Evolutionary algorithm:
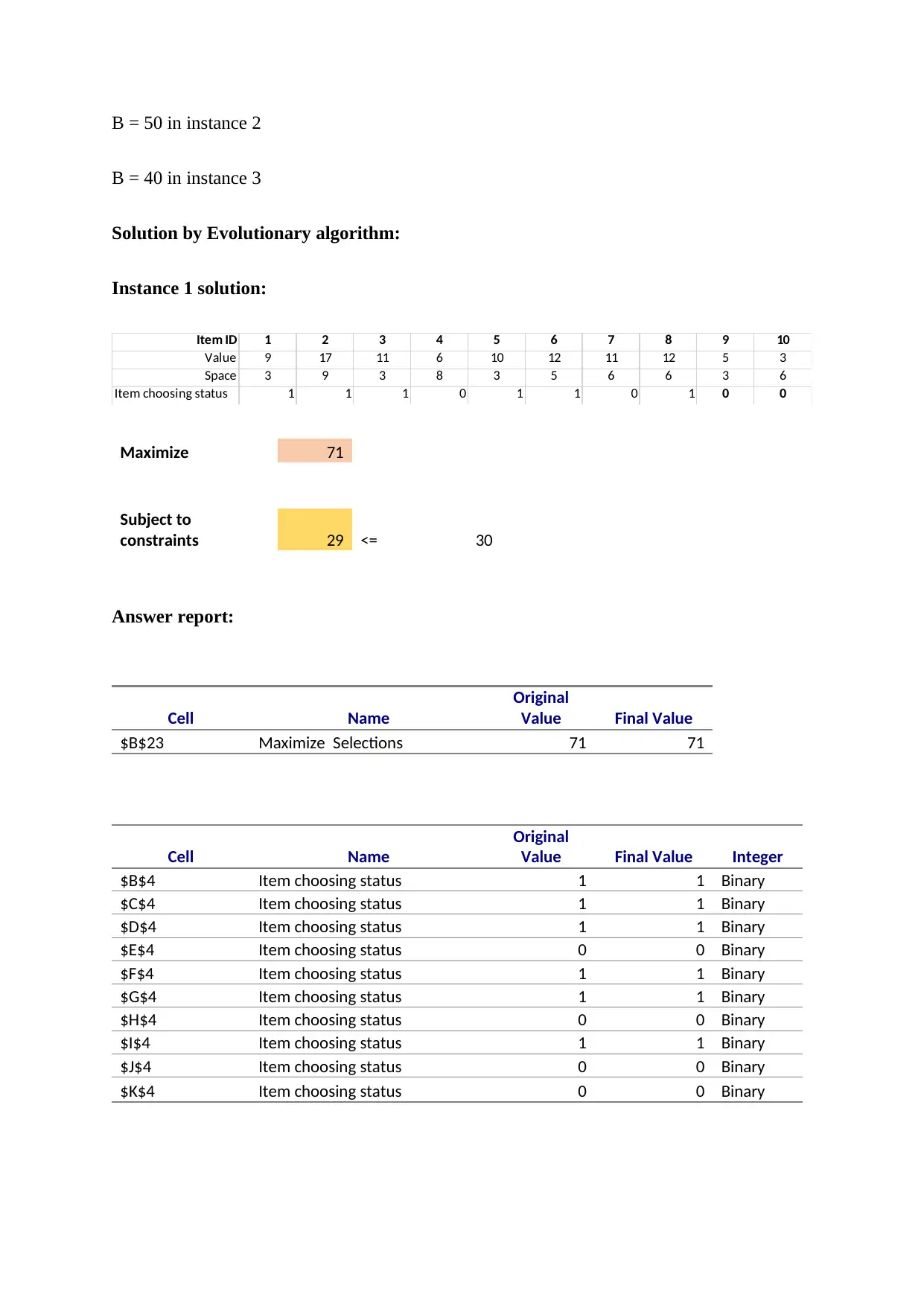
Instance 1 solution:
Item ID 1 2 3 4 5 6 7 8 9 10
Value 9 17 11 6 10 12 11 12 5 3
Space 3 9 3 8 3 5 6 6 3 6
Item choosing status 1 1 1 0 1 1 0 1 0 0
Maximize 71
Subject to
constraints 29 <= 30
Answer report:
Cell Name
Original
Value Final Value
$B$23 Maximize Selections 71 71
Cell Name
Original
Value Final Value Integer
$B$4 Item choosing status 1 1 Binary
$C$4 Item choosing status 1 1 Binary
$D$4 Item choosing status 1 1 Binary
$E$4 Item choosing status 0 0 Binary
$F$4 Item choosing status 1 1 Binary
$G$4 Item choosing status 1 1 Binary
$H$4 Item choosing status 0 0 Binary
$I$4 Item choosing status 1 1 Binary
$J$4 Item choosing status 0 0 Binary
$K$4 Item choosing status 0 0 Binary

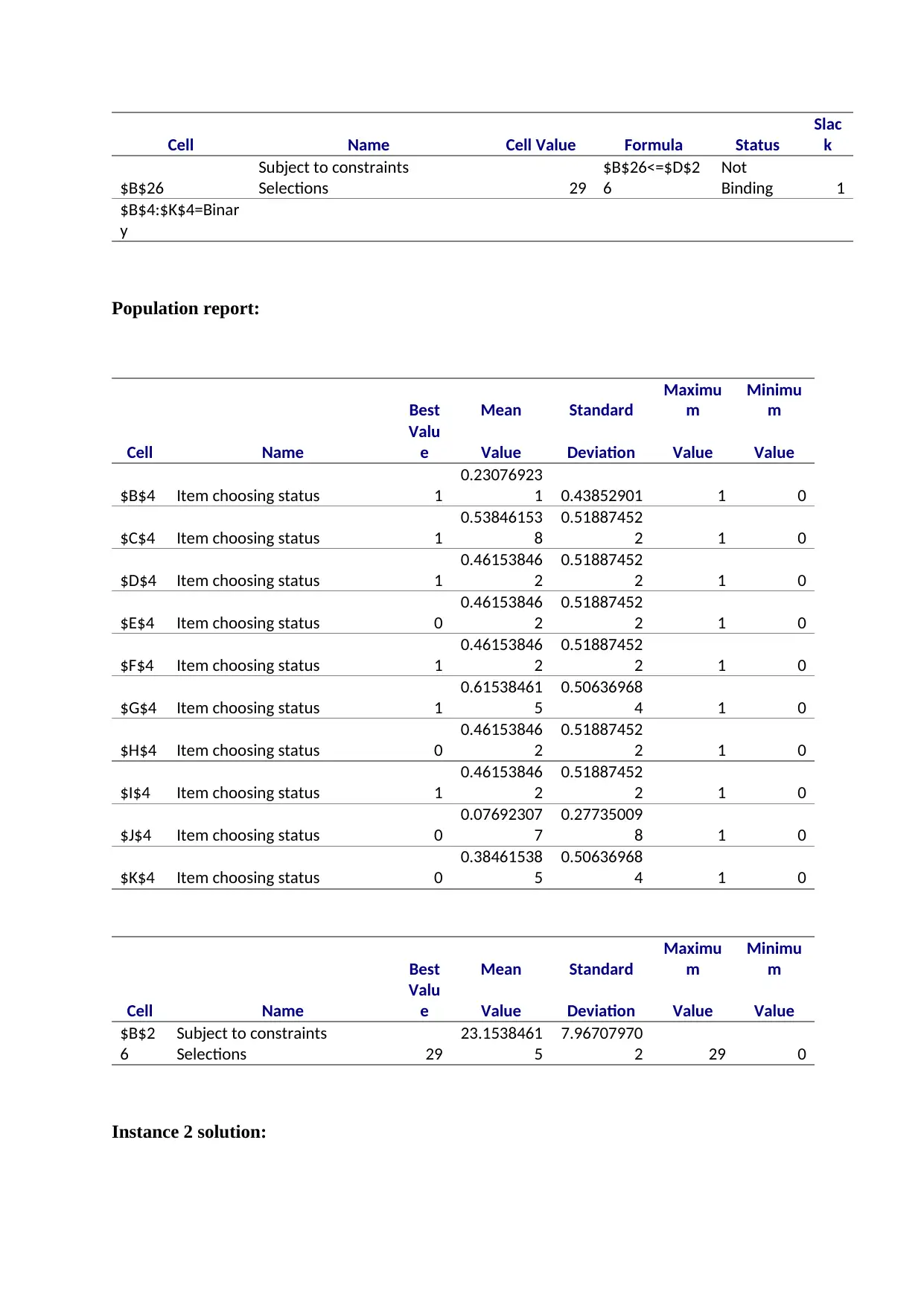
Cell Name Cell Value Formula Status
Slac
k
$B$26
Subject to constraints
Selections 29
$B$26<=$D$2
6
Not
Binding 1
$B$4:$K$4=Binar
y
Population report:
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$4 Item choosing status 1
0.23076923
1 0.43852901 1 0
$C$4 Item choosing status 1
0.53846153
8
0.51887452
2 1 0
$D$4 Item choosing status 1
0.46153846
2
0.51887452
2 1 0
$E$4 Item choosing status 0
0.46153846
2
0.51887452
2 1 0
$F$4 Item choosing status 1
0.46153846
2
0.51887452
2 1 0
$G$4 Item choosing status 1
0.61538461
5
0.50636968
4 1 0
$H$4 Item choosing status 0
0.46153846
2
0.51887452
2 1 0
$I$4 Item choosing status 1
0.46153846
2
0.51887452
2 1 0
$J$4 Item choosing status 0
0.07692307
7
0.27735009
8 1 0
$K$4 Item choosing status 0
0.38461538
5
0.50636968
4 1 0
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$2
6
Subject to constraints
Selections 29
23.1538461
5
7.96707970
2 29 0
Instance 2 solution:

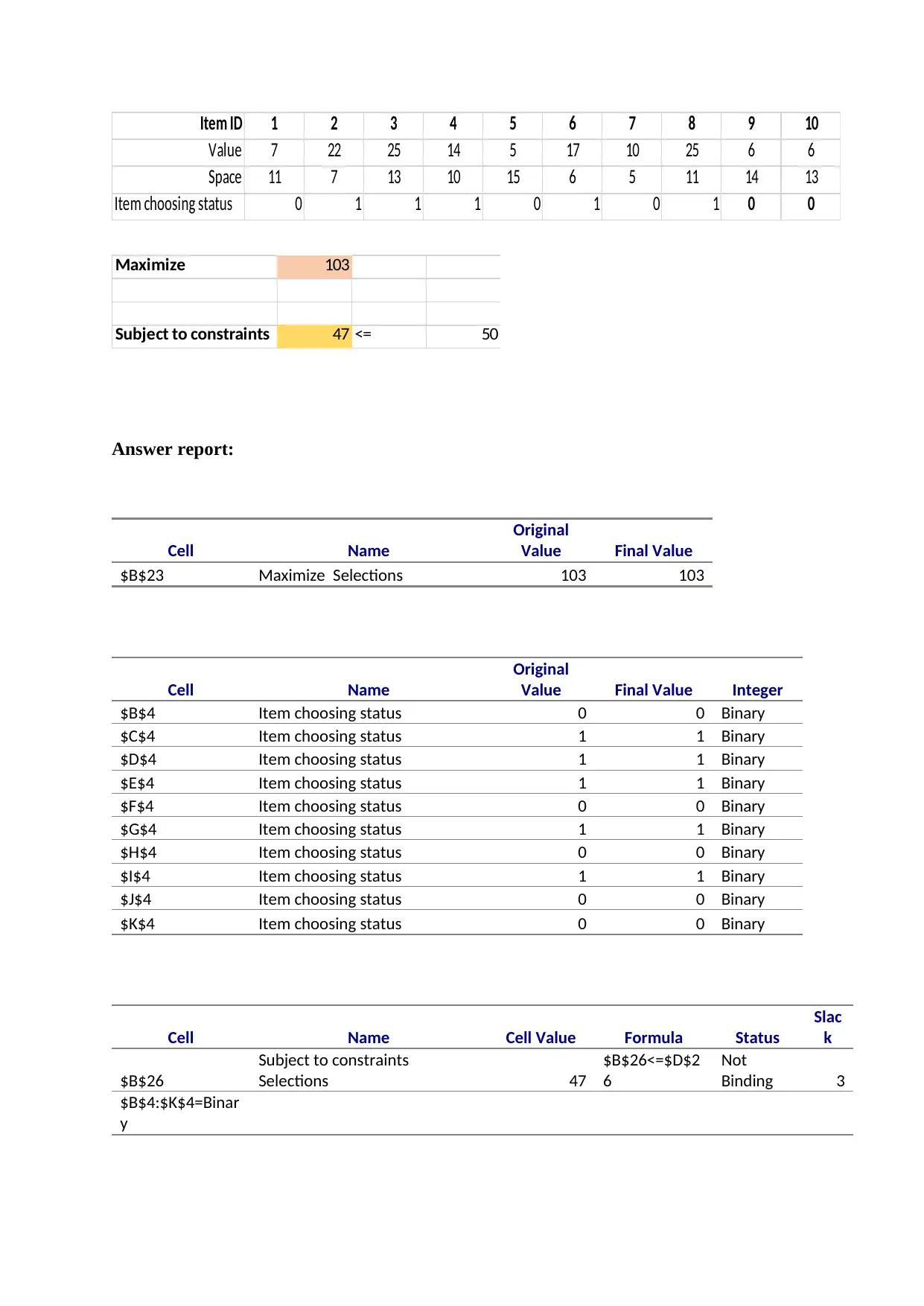
Item ID 1 2 3 4 5 6 7 8 9 10
Value 7 22 25 14 5 17 10 25 6 6
Space 11 7 13 10 15 6 5 11 14 13
Item choosing status 0 1 1 1 0 1 0 1 0 0
Maximize 103
Subject to constraints 47 <= 50
Answer report:
Cell Name
Original
Value Final Value
$B$23 Maximize Selections 103 103
Cell Name
Original
Value Final Value Integer
$B$4 Item choosing status 0 0 Binary
$C$4 Item choosing status 1 1 Binary
$D$4 Item choosing status 1 1 Binary
$E$4 Item choosing status 1 1 Binary
$F$4 Item choosing status 0 0 Binary
$G$4 Item choosing status 1 1 Binary
$H$4 Item choosing status 0 0 Binary
$I$4 Item choosing status 1 1 Binary
$J$4 Item choosing status 0 0 Binary
$K$4 Item choosing status 0 0 Binary
Cell Name Cell Value Formula Status
Slac
k
$B$26
Subject to constraints
Selections 47
$B$26<=$D$2
6
Not
Binding 3
$B$4:$K$4=Binar
y

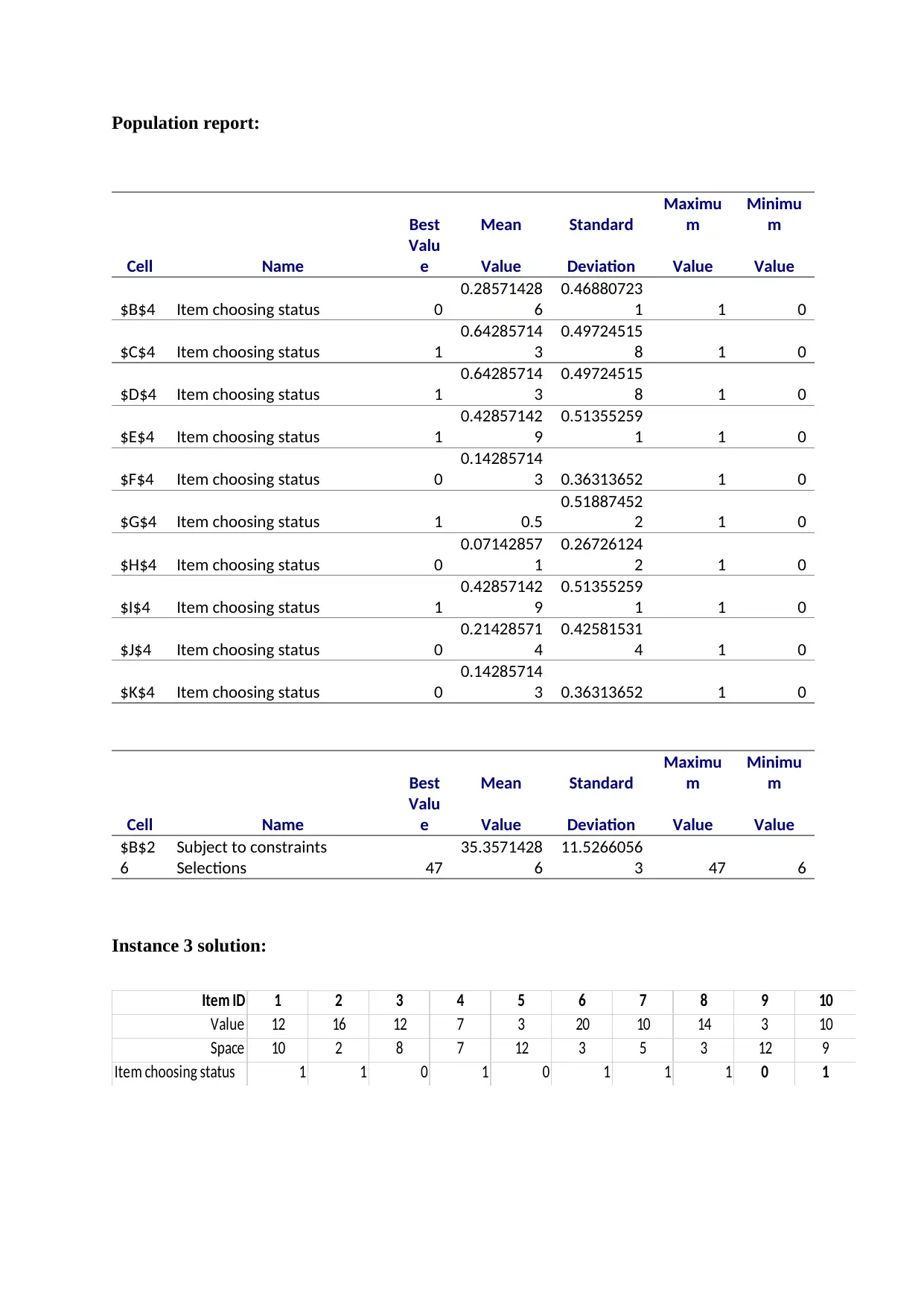
Population report:
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$4 Item choosing status 0
0.28571428
6
0.46880723
1 1 0
$C$4 Item choosing status 1
0.64285714
3
0.49724515
8 1 0
$D$4 Item choosing status 1
0.64285714
3
0.49724515
8 1 0
$E$4 Item choosing status 1
0.42857142
9
0.51355259
1 1 0
$F$4 Item choosing status 0
0.14285714
3 0.36313652 1 0
$G$4 Item choosing status 1 0.5
0.51887452
2 1 0
$H$4 Item choosing status 0
0.07142857
1
0.26726124
2 1 0
$I$4 Item choosing status 1
0.42857142
9
0.51355259
1 1 0
$J$4 Item choosing status 0
0.21428571
4
0.42581531
4 1 0
$K$4 Item choosing status 0
0.14285714
3 0.36313652 1 0
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$2
6
Subject to constraints
Selections 47
35.3571428
6
11.5266056
3 47 6
Instance 3 solution:
Item ID 1 2 3 4 5 6 7 8 9 10
Value 12 16 12 7 3 20 10 14 3 10
Space 10 2 8 7 12 3 5 3 12 9
Item choosing status 1 1 0 1 0 1 1 1 0 1

Maximize 89
Subject to constraints 39 <= 40
Answer report:
Cell Name
Original
Value Final Value
$B$23 Maximize Selections 0 89
Cell Name
Original
Value Final Value Integer
$B$4 Item choosing status 0 1 Binary
$C$4 Item choosing status 0 1 Binary
$D$4 Item choosing status 0 0 Binary
$E$4 Item choosing status 0 1 Binary
$F$4 Item choosing status 0 0 Binary
$G$4 Item choosing status 0 1 Binary
$H$4 Item choosing status 0 1 Binary
$I$4 Item choosing status 0 1 Binary
$J$4 Item choosing status 0 0 Binary
$K$4 Item choosing status 0 1 Binary
Cell Name Cell Value Formula Status
Slac
k
$B$26
Subject to constraints
Selections 39
$B$26<=$D$2
6
Not
Binding 1
$B$4:$K$4=Binar
y
Population report:
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$4 Item choosing status 1 0.57142857 0.51355259 1 0

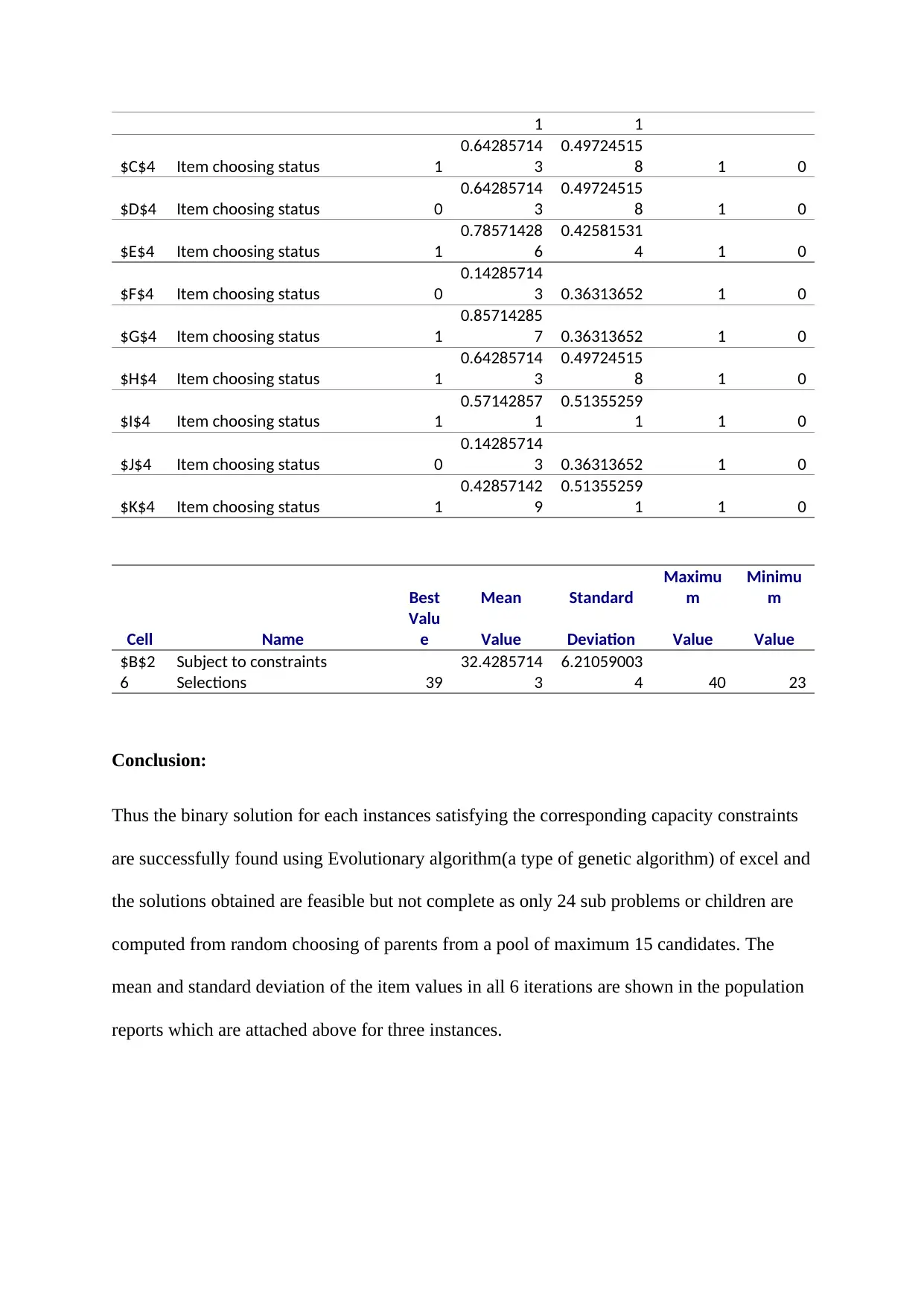
1 1
$C$4 Item choosing status 1
0.64285714
3
0.49724515
8 1 0
$D$4 Item choosing status 0
0.64285714
3
0.49724515
8 1 0
$E$4 Item choosing status 1
0.78571428
6
0.42581531
4 1 0
$F$4 Item choosing status 0
0.14285714
3 0.36313652 1 0
$G$4 Item choosing status 1
0.85714285
7 0.36313652 1 0
$H$4 Item choosing status 1
0.64285714
3
0.49724515
8 1 0
$I$4 Item choosing status 1
0.57142857
1
0.51355259
1 1 0
$J$4 Item choosing status 0
0.14285714
3 0.36313652 1 0
$K$4 Item choosing status 1
0.42857142
9
0.51355259
1 1 0
Best Mean Standard
Maximu
m
Minimu
m
Cell Name
Valu
e Value Deviation Value Value
$B$2
6
Subject to constraints
Selections 39
32.4285714
3
6.21059003
4 40 23
Conclusion:
Thus the binary solution for each instances satisfying the corresponding capacity constraints
are successfully found using Evolutionary algorithm(a type of genetic algorithm) of excel and
the solutions obtained are feasible but not complete as only 24 sub problems or children are
computed from random choosing of parents from a pool of maximum 15 candidates. The
mean and standard deviation of the item values in all 6 iterations are shown in the population
reports which are attached above for three instances.