La Roche University, Calculus I Homework #7 Solution

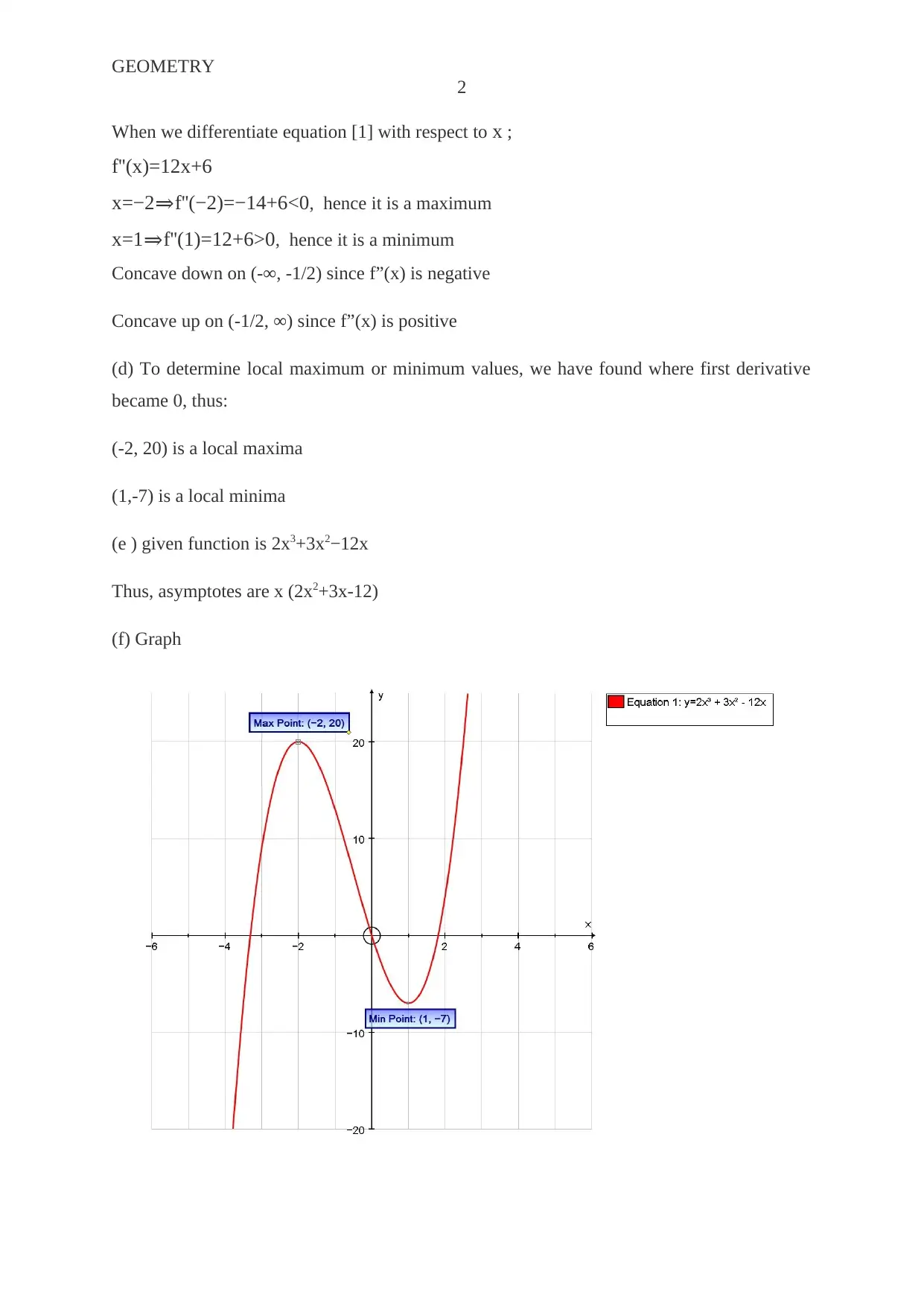
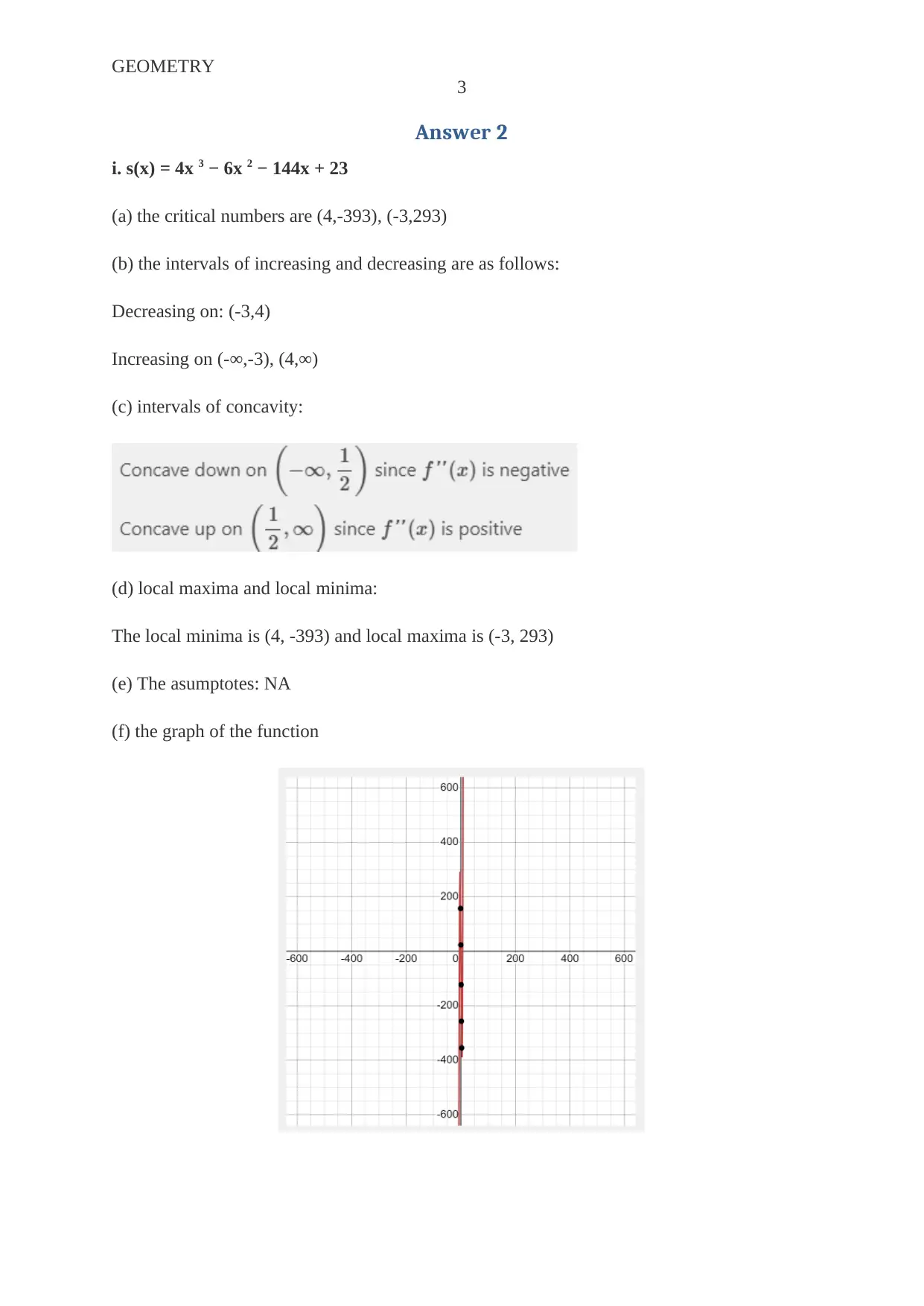
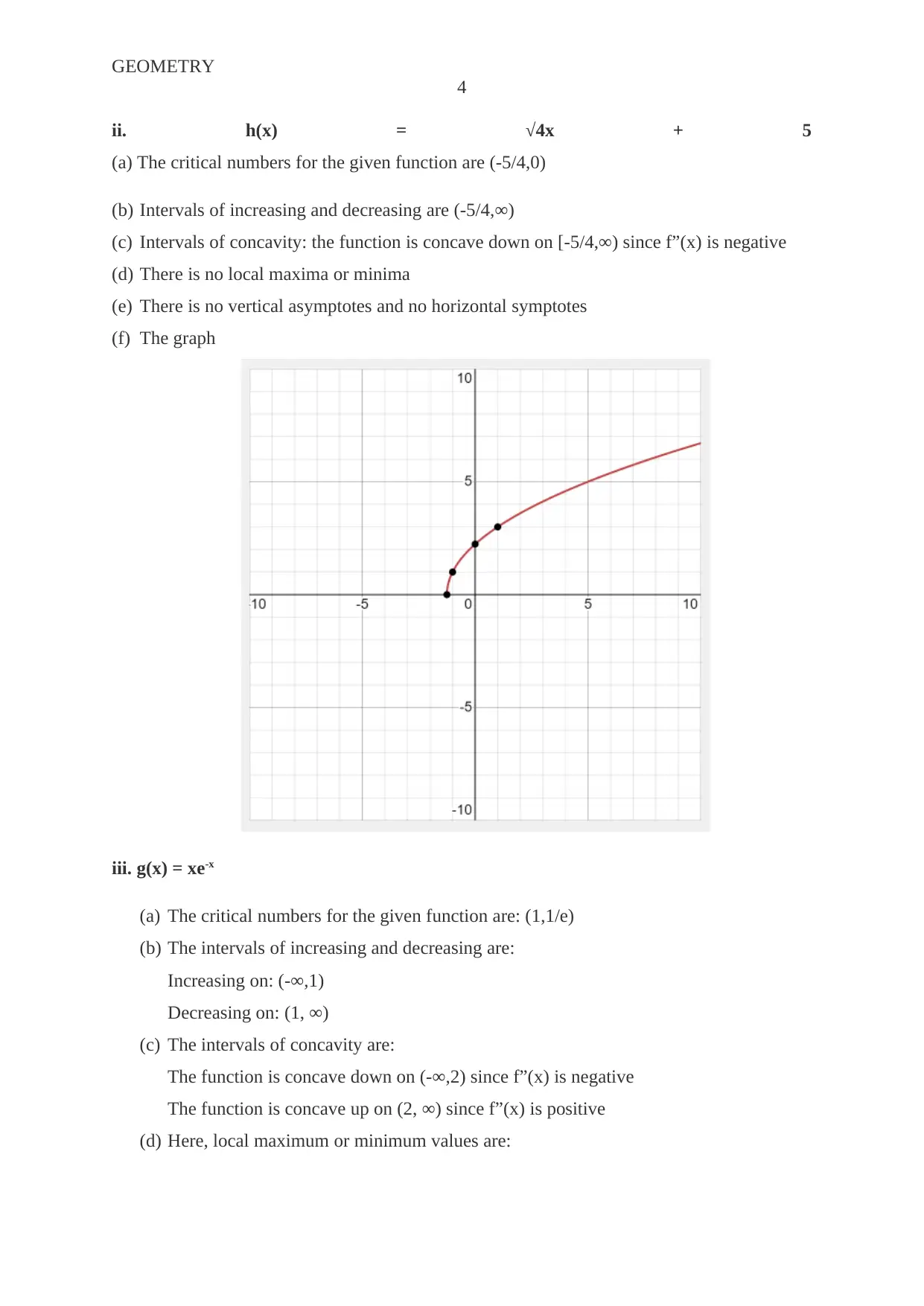
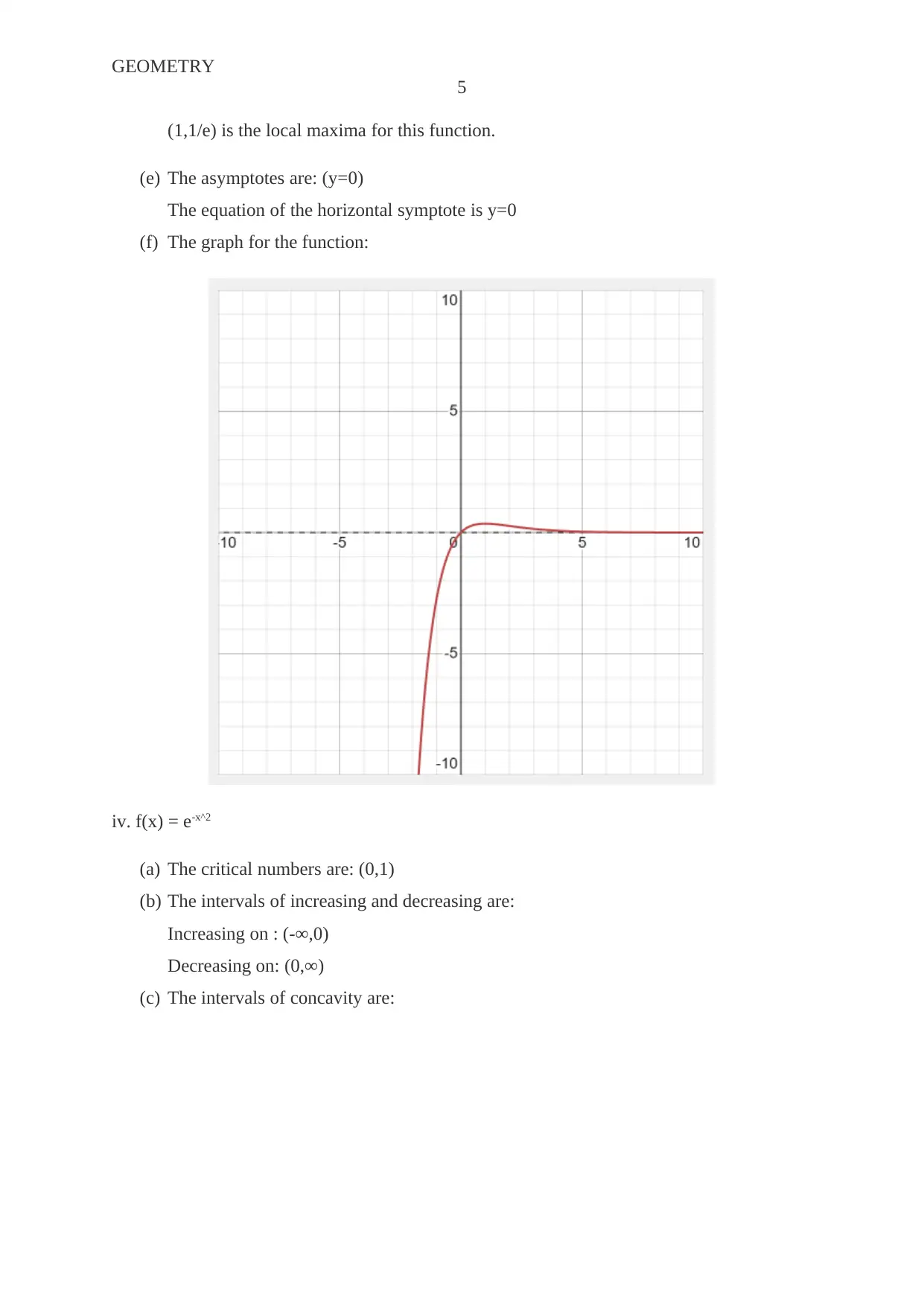
This document presents a comprehensive solution to a calculus homework assignment from La Roche University's Math 1032 course. The assignment focuses on analyzing various functions, including determining critical numbers, identifying intervals of increasing and decreasing behavior, finding intervals of concavity, and locating local maxima and minima. Solutions are provided for several functions, including polynomial, square root, and exponential functions, along with the identification of asymptotes and the creation of corresponding graphs. The document demonstrates the application of calculus principles to analyze and visualize function behavior, offering detailed step-by-step explanations and graphical representations to aid in understanding. The solutions cover the application of derivatives and second derivatives to understand the characteristics of functions, providing a complete solution to the assigned problems.

Running Head: GEOMETRY
0
Geometry and Calculus
(Student Details: )
3/28/2020

GEOMETRY
1
Answer 1
Given function: f(x)=2x3+3x2−12x
(a) critical numbers are (−1,20) and (1,−7) out of which, (−1,20) is the maximum and
(1,−7) is a minimum.
It can be explained as below:
Now, while differentiating with respect to x' we have found:
f'(x)=6x2+6x−12 [1]
if we find value of above function at a critical point, f'(x)=0
f'(x)=0⇒6x2+6x−12=0
x2+x−2=0
(x+2)(x−1)=0
x=−2,1
Now, finding y-coordinate will require substituting these values into f(x)
x=−2⇒f(−2)=2(−8)+3(4)−12(−2)=−16+12+24=20
x=1⇒f(1)=2+3−12=−7
So the critical points are (−1,20) and (1,−7)
(b) As per the given function f(x)= 2x3+3x2−12x
In order to find the critical numbers, first we found values of x st f'(x)=0
Thus, we have determined the intervals of increasing and decreasing of the given function.
(c ) To find intervals of concavity, we have found where the plotted curve of the given
function is concave up or concave down. Thus, intervals of concavity are as follows:

GEOMETRY
2
When we differentiate equation [1] with respect to x ;
f''(x)=12x+6
x=−2⇒f''(−2)=−14+6<0, hence it is a maximum
x=1⇒f''(1)=12+6>0, hence it is a minimum
Concave down on (-∞, -1/2) since f”(x) is negative
Concave up on (-1/2, ∞) since f”(x) is positive
(d) To determine local maximum or minimum values, we have found where first derivative
became 0, thus:
(-2, 20) is a local maxima
(1,-7) is a local minima
(e ) given function is 2x3+3x2−12x
Thus, asymptotes are x (2x2+3x-12)
(f) Graph

GEOMETRY
3
Answer 2
i. s(x) = 4x 3 − 6x 2 − 144x + 23
(a) the critical numbers are (4,-393), (-3,293)
(b) the intervals of increasing and decreasing are as follows:
Decreasing on: (-3,4)
Increasing on (-∞,-3), (4,∞)
(c) intervals of concavity:
(d) local maxima and local minima:
The local minima is (4, -393) and local maxima is (-3, 293)
(e) The asumptotes: NA
(f) the graph of the function

GEOMETRY
4
ii. h(x) = √4x + 5
(a) The critical numbers for the given function are (-5/4,0)
(b) Intervals of increasing and decreasing are (-5/4,∞)
(c) Intervals of concavity: the function is concave down on [-5/4,∞) since f”(x) is negative
(d) There is no local maxima or minima
(e) There is no vertical asymptotes and no horizontal symptotes
(f) The graph
iii. g(x) = xe-x
(a) The critical numbers for the given function are: (1,1/e)
(b) The intervals of increasing and decreasing are:
Increasing on: (-∞,1)
Decreasing on: (1, ∞)
(c) The intervals of concavity are:
The function is concave down on (-∞,2) since f”(x) is negative
The function is concave up on (2, ∞) since f”(x) is positive
(d) Here, local maximum or minimum values are:

GEOMETRY
5
(1,1/e) is the local maxima for this function.
(e) The asymptotes are: (y=0)
The equation of the horizontal symptote is y=0
(f) The graph for the function:
iv. f(x) = e-x^2
(a) The critical numbers are: (0,1)
(b) The intervals of increasing and decreasing are:
Increasing on : (-∞,0)
Decreasing on: (0,∞)
(c) The intervals of concavity are:

GEOMETRY
6
(d) The local maximum or minimum values are found as:
There is no local minima and the local maxima is (0,1)
(e) The asymptotes for the given function are: (y=0) which is a horizontal asymptote.
(f) The graph for the given function is:
v. f(x) = (2x2 − 3x)/ (x – 2)
(a) the critical numbers are: (3, 9), (1, 1)
(b) for the given function, the intervals of increasing and decreasing are:
Decreasing on : (1, 2), (2, 3)
Increasing on : (-∞, 1) , (3, ∞)
(c) the intervals of concavity are:

GEOMETRY
7
Concave down on (-∞, 2) since f”(x) is negative
Concave up on (2, ∞) since f”(x) is positive
(d) the local maximum or minimum values are:
Local minima is (3, 9) and local maxima is (1,1)
(e) asymptotes are:
Oblique asymptotes: y=2x+1
Horizontal asymtotes: NA
Vertical asymptotes: x=2
(f) the graph for the given function is:
vi. f(x) = arctan(x)
(a) There are critical numbers in this function

GEOMETRY
8
(b) The intervals of increasing and decreasing suggest that the given function is always
increasing.
(c) The intervals of concavity:
(d) The local maximum or minimum values: there is no local maxima and minima as
function is always increasing.
(e) The asymptotes for the given function are:
(f) The graph is:

GEOMETRY
9
References
Flanders, H. and Price, J.J., 2014. Calculus with analytic geometry. Academic Press.
Boyer, C.B., 2012. History of analytic geometry. Courier Corporation.
Woods, F.S., 2013. Higher geometry: an introduction to advanced methods in analytic
geometry. Courier Corporation.
Macdonald, A., 2017. A survey of geometric algebra and geometric calculus. Advances in
Applied Clifford Algebras, 27(1), pp.853-891.