Vector Space Analysis: Linear Combinations and Independence Tasks

This assignment explores fundamental concepts in linear algebra, focusing on vector spaces, linear combinations, linear independence, and the determination of a basis. It includes problems involving finding linear combinations of vectors, determining the rank and basis of vector spaces, testing sets of vectors for linear independence or dependence, and determining the dimension and basis of spaces spanned by given vectors. The problems are solved using MATLAB, with code snippets provided for each question, demonstrating how to perform the necessary calculations and analyses. Desklib provides students with access to this solved assignment and many other resources, including past papers, to help them succeed in their studies.

Table of Contents
........................................................................................................................................ 1
Question 1 ......................................................................................................................... 1
Question 2 ......................................................................................................................... 2
Question 3 ......................................................................................................................... 3
Question 4 ......................................................................................................................... 4
Question 5 ......................................................................................................................... 7
format short
clear
close all
clc
Question 1
disp('-------------------------------------------------------------------')
disp('Question 1 Loading...')
%Part a
u1=[1;1;2;2];
u2=[2;3;5;6];
u3=[2;1;3;6];
u=[u1 u2 u3];
v=[0;5;3;0];
X=u\v % determines the linear combination coordinates for each value
disp('For the First output')
fprintf('%.3fu1+ %.3fu2 %.3fu3 \n ',X(1),X(2),X(3));
%Part B
vr=[1;6;1;4];
Xb=u\vr; % determines the linear combination coordinates for each
value
disp('For the second output')
fprintf('%.1fu1+ %.1fu2 %.1fu3 \n ',Xb(1),Xb(2),Xb(3));
-------------------------------------------------------------------
Question 1 Loading...
X =
-2.0000
2.8333
-2.1667
For the First output
-2.000u1+ 2.833u2 -2.167u3
For the second output
-7.0u1+ 4.0u2 -1.0u3
1

Question 2
clear
disp('-------------------------------------------------------------------')
disp('Question 2 Loading...')
q1=[1;-2;3;4];
q2=[2;4;5;0];
q3=[-1;0;0;4];
q4=[3;2;1;-4];
q=[q1 q2 q3 q4]
rank(q) %determining the rank of a vector
Qr=rref(q) %Determining the basis of a vector space
%part 2
e1=[0;1;1;1];
e2=[2;2;3;1];
e3=[7;0;1;0];
e4=[5;2;2;1];
e=[e1 e2 e3 e4]
rank(e) %determining the rank of a vector
Er=rref(e) %Determining the basis of a vector space
-------------------------------------------------------------------
Question 2 Loading...
q =
1 2 -1 3
-2 4 0 2
3 5 0 1
4 0 4 -4
ans =
4
Qr =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
e =
0 2 7 5
1 2 0 2
2

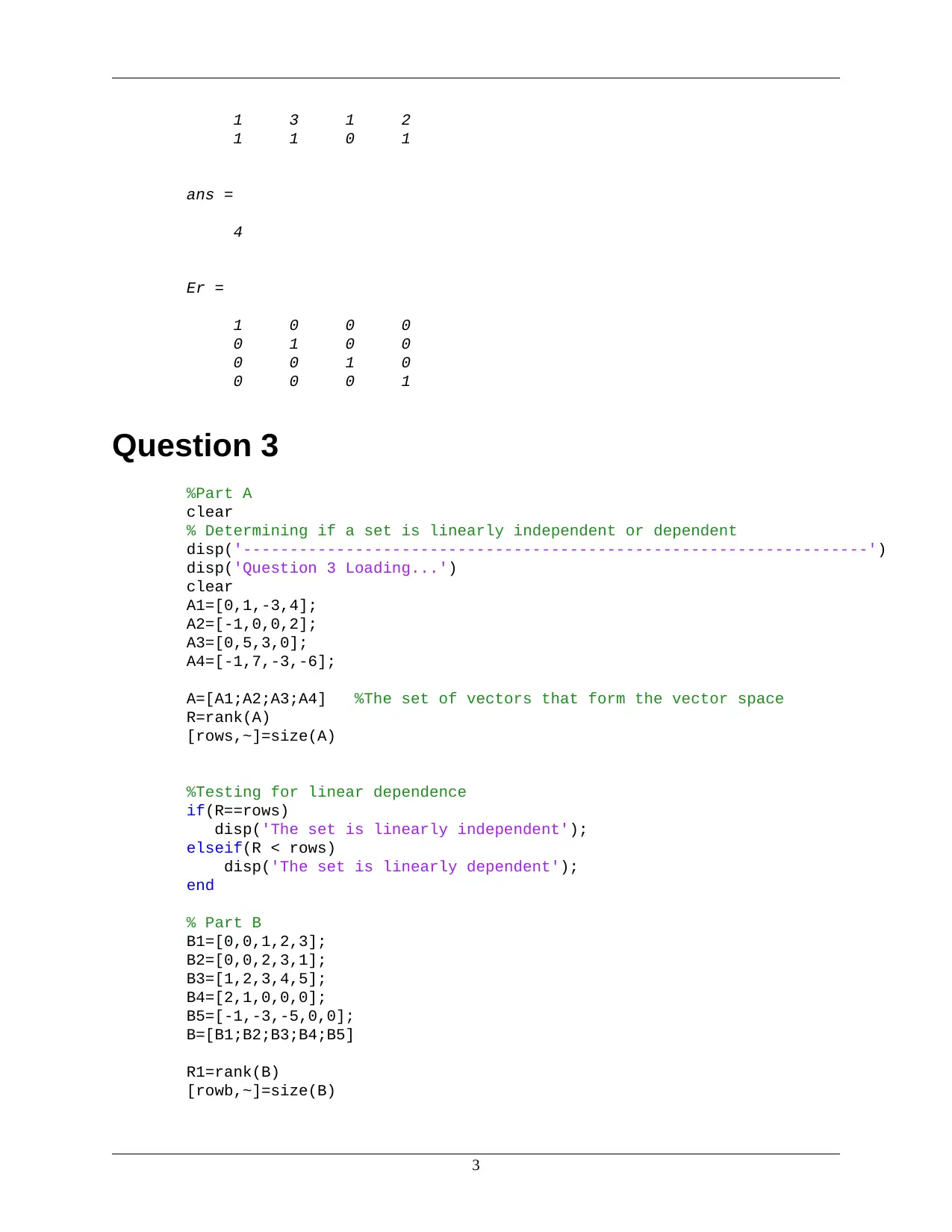
1 3 1 2
1 1 0 1
ans =
4
Er =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Question 3
%Part A
clear
% Determining if a set is linearly independent or dependent
disp('-------------------------------------------------------------------')
disp('Question 3 Loading...')
clear
A1=[0,1,-3,4];
A2=[-1,0,0,2];
A3=[0,5,3,0];
A4=[-1,7,-3,-6];
A=[A1;A2;A3;A4] %The set of vectors that form the vector space
R=rank(A)
[rows,~]=size(A)
%Testing for linear dependence
if(R==rows)
disp('The set is linearly independent');
elseif(R < rows)
disp('The set is linearly dependent');
end
% Part B
B1=[0,0,1,2,3];
B2=[0,0,2,3,1];
B3=[1,2,3,4,5];
B4=[2,1,0,0,0];
B5=[-1,-3,-5,0,0];
B=[B1;B2;B3;B4;B5]
R1=rank(B)
[rowb,~]=size(B)
3

%Testing for linear dependence
if(R1==rowb)
disp('The set is linearly independent');
elseif(R1 < rowb)
disp('The set is linearly dependent');
end
-------------------------------------------------------------------
Question 3 Loading...
A =
0 1 -3 4
-1 0 0 2
0 5 3 0
-1 7 -3 -6
R =
4
rows =
4
The set is linearly independent
B =
0 0 1 2 3
0 0 2 3 1
1 2 3 4 5
2 1 0 0 0
-1 -3 -5 0 0
R1 =
5
rowb =
5
The set is linearly independent
Question 4
part A
4

... A subset S of a vector space is a basis if S is linearly
independent
... and S is a spanning set.
clear
disp('-------------------------------------------------------------------')
disp('Question 4 Loading...')
A1=[1,-2,3,4];
A2=[2,4,5,0];
A3=[-2,0,0,4];
A4=[3,2,1,-4];
A=[A1;A2;A3;A4]
% To determine the dimension of the space spanned by the columns
rank(A)
%To determine the basis of the columns
Ar=rref(A)
% Part B
B1=[0,1,-1,1];
B2=[2,-2,3,1];
B3=[7,0,1,0];
B4=[5,2,-2,-1];
B=[B1;B2;B3;B4]
% To determine the dimension of the space spanned by the columns
rank(B)
%To determine the basis of the columns
Br=rref(B)
% Part C
C1=[0,1,-3,4];
C2=[-1,0,0,2];
C3=[0,5,3,0];
C4=[-1,7,-3,-6];
C=[C1;C2;C3;C4]
% To determine the dimension of the space spanned by the columns
rank(C)
%To determine the basis of the columns
Cr=rref(C)
% Part D
D1=[0,0,1,2];
D2=[0,2,3,1];
D3=[1,3,4,5];
D4=[2,1,0,0];
D5=[-3,-5,0,0];
D=[D1;D2;D3;D4;D5]
% To determine the dimension of the space spanned by the columns
rank(D)
%To determine the basis of the columns
Dr=rref(D)
-------------------------------------------------------------------
5

Question 4 Loading...
A =
1 -2 3 4
2 4 5 0
-2 0 0 4
3 2 1 -4
ans =
4
Ar =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
B =
0 1 -1 1
2 -2 3 1
7 0 1 0
5 2 -2 -1
ans =
3
Br =
1.0000 0 0 -0.6000
0 1.0000 0 5.2000
0 0 1.0000 4.2000
0 0 0 0
C =
0 1 -3 4
-1 0 0 2
0 5 3 0
-1 7 -3 -6
ans =
6

4
Cr =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
D =
0 0 1 2
0 2 3 1
1 3 4 5
2 1 0 0
-3 -5 0 0
ans =
4
Dr =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
0 0 0 0
Question 5
clear
disp('-------------------------------------------------------------------')
disp('Question 5 Loading...')
%Part A
v1=[2;1;0;0;0];
v2=[-1;0;1;0;0];
B=[v1,v2];
B1=eye(5);
% adjoining B and B1
A=[B,B1]
rank(A)
At=rref(A)
% The results show that columns 1,2,3,6,7 for the basis for R^5
At(:,4)=[]; %removing column 4
At(:,4)=[]; %removing column 5
disp('The basis of the vector space is:')
7

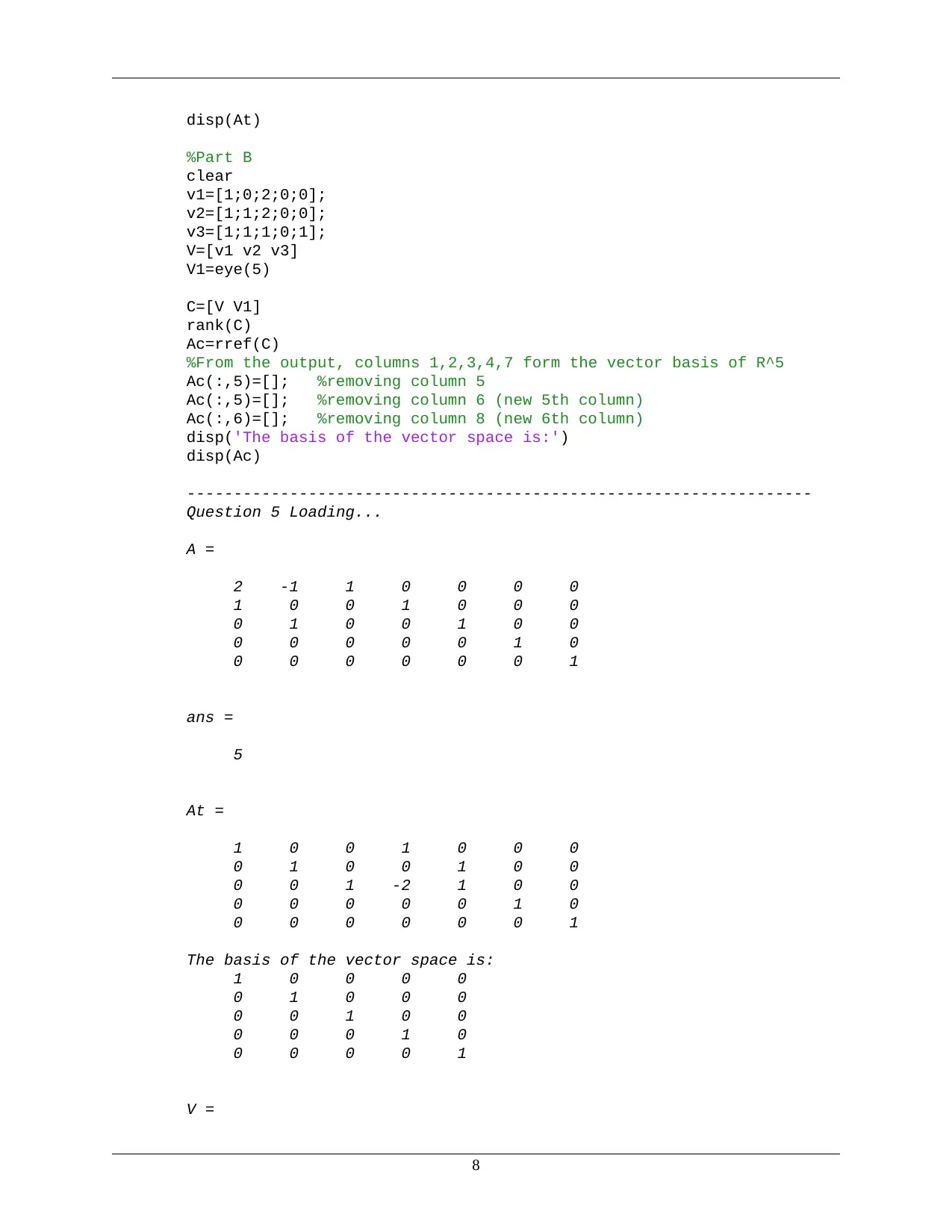
disp(At)
%Part B
clear
v1=[1;0;2;0;0];
v2=[1;1;2;0;0];
v3=[1;1;1;0;1];
V=[v1 v2 v3]
V1=eye(5)
C=[V V1]
rank(C)
Ac=rref(C)
%From the output, columns 1,2,3,4,7 form the vector basis of R^5
Ac(:,5)=[]; %removing column 5
Ac(:,5)=[]; %removing column 6 (new 5th column)
Ac(:,6)=[]; %removing column 8 (new 6th column)
disp('The basis of the vector space is:')
disp(Ac)
-------------------------------------------------------------------
Question 5 Loading...
A =
2 -1 1 0 0 0 0
1 0 0 1 0 0 0
0 1 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
ans =
5
At =
1 0 0 1 0 0 0
0 1 0 0 1 0 0
0 0 1 -2 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
The basis of the vector space is:
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
V =
8

1 1 1
0 1 1
2 2 1
0 0 0
0 0 1
V1 =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
C =
1 1 1 1 0 0 0 0
0 1 1 0 1 0 0 0
2 2 1 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1
ans =
5
Ac =
Columns 1 through 7
1.0000 0 0 0 -1.0000 0.5000 0
0 1.0000 0 0 1.0000 0 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 -0.5000 0
0 0 0 0 0 0 1.0000
Column 8
0.5000
-1.0000
1.0000
-0.5000
0
The basis of the vector space is:
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
9

0 0 0 0 1
Published with MATLAB® R2018b
10