Linear Algebra Assignment: Vector Spaces, Norms, and Transformations

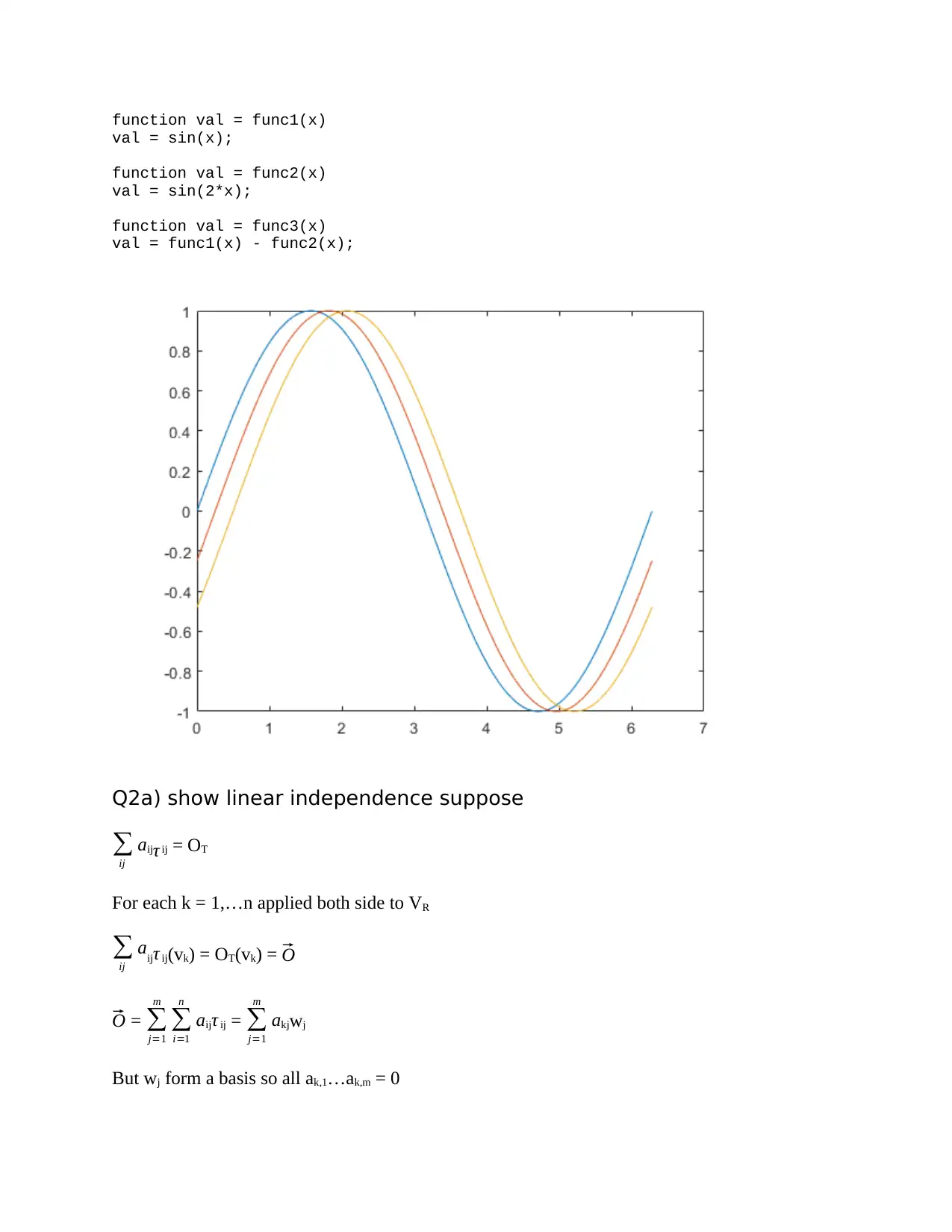
This document provides a comprehensive solution to a linear algebra assignment. The solution addresses several core concepts, including linear independence, Taylor series expansions, and the distinction between distances and norms. It also includes code for plotting functions and analyzing the impact of different norms. Furthermore, the assignment delves into linear transformations, demonstrating linear independence and spanning, and explores the relationship between matrices and transformations. The solution also covers dual spaces, proving that the double dual of a vector space is isomorphic to the original space. Finally, the assignment investigates the linearity of transformations and provides detailed explanations for each problem.

Q1a) ||x – y||2 = ∫
0
1
¿ ¿
We say that vector v1….vk∈ τ
are linear independent if a0v0 + a1v1…..akvk = ⃗ 0 scalars ai ∈ S
but we have
(-1)v1 + a2v2 + …anvn = ⃗ 0
Since this is a non trival linear combination, S is linearly dependent
If n = 1 and v1 ∈ span (span/{v1} then v1 ∈ span ({}) = {⃗ 0}
b)
f(t) = 1 + t + t2/2
F(t) = (t – a)0/0! * f(a) + (t – a)1/1! + (t – a)2/2! + …
F1(t) = 1 + t
F1(a) = 1 + a
Calculate the second order differential
F11(t) = 1
F11(a) = 1
Substituting the value
F(t) = (t – a)0/0! * f(a) + (t – a)1/1! + (t – a)2/2! + …
Taylor series at a = 0
F(t) = t2 + t2/3 + 2t6/15 + ….
Expression for f(t0) using Taylor series
F(t0) = f(t0) + E1(0)
Writing equation for f(t0 + h) using Taylor series
F(t0+h) – f(t0) = f(t0) + hf1(t0) ) E1(h)
Substituting
F(t0+h) – f(t0) = f(t0) + hf1(t0) ) E1(h) – {f(t0) + E1(0)}
F1(t0) = 1/h((f(t0 + h) – f(t0)) + {E1(h) – E1(0)}

Obtaining truncation error from above equation
E = {E1(h) – E1(0)}
c)
a distance is a function
d:X×X⟶R+
while a norm is a function:
∥⋅∥X⟶R+
So a norm always induces a distance by:
d(x,y)=∥x−y∥
However, the other way around is not always true. For a distance to come from a norm, it needs
to verifiy:
d(αx,αy)=|α|d(x,y)
If we take the discrete distance on any space:
d(x,y)= {1if x= y
0 if x ≠ y
Then this distance does not verify the condition, for example for α=2
d) Now plot x(t) and ^x(t) and comment on the difference this norm makes.
function test
clc
clear all
x = -pi:0.01:pi;
subplot(1,2,1)
plot(x, func1(x), x, func2(x))
hold on
plot(x, func3(x), 'r-', 'LineWidth', 2)
title('Using standard function definition')
subplot(1,2,2)
plot(x, func1(x), x, func2(x))
hold on
func4 = @(x) func1(x) - func2(x);
plot(x, func4(x), 'r-', 'LineWidth', 2)
title('Using anonymous function')

function val = func1(x)
val = sin(x);
function val = func2(x)
val = sin(2*x);
function val = func3(x)
val = func1(x) - func2(x);
Q2a) show linear independence suppose
∑
ij
aijτ ij = OT
For each k = 1,…n applied both side to VR
∑
ij
aijτ ij(vk) = OT(vk) = ⃗ O⃗
O = ∑
j=1
m
∑
i=1
n
aijτ ij = ∑
j=1
m
akjwj
But wj form a basis so all ak,1…ak,m = 0

Showing spanning purpose τ : V →W is linear, then i= 1…n the vector τ ¿vi) is w
τ ¿vi) = ai,1w1 + …ai,mwm
Hence the transformation
ˇτ = ∑
ij
aijτ ij
We claim that this is equal τ
τ ¿vi) = ai,1w1 + …ai,mwm
ˇτ (vk) = ∑
ij
aijτ ij(vk) = ∑
j=1
m
∑
i=1
n
aijτ ij(vk)
= ∑
j=1
m
akjwj
= ak,1w1 +…ak,mwm
b) X = [ x 1,1 x 1,2 .. x 1, N
x 2,1 x 2,2 .. x 2, N
x N , 1 x N , 1 .. x N , N ] = [T]βγ[v]β
Suppose A and B are 2 matrices such as v ∈V
A[v]β = [T(v)]γ = B[v]β
Take v = vk, then [v]β = ek and A[v]β is the kth column of A
Therefore, A and B have all the column, this means A = B
c) since ɸ is an isommer ɸ ( β ) isa basis of V ¿∗¿¿
ɸ(vi)(fvk) = fvk(vi)
which is 1 if I = k and 0 otherwise. This mean ɸ(β) = β**
if W is a subspace, let w ∈W ,letting f ∈ W ⟘
ɸ(w)(f) = f(w) =0
so w ∈ ( w❑ )⟘ since ɸ is an isomorphism ɸ(w) is a subspace of (w⟘)⟘

d)
X =
[ a 0,0 a 1,2 ..a 0 , N
2−1
a 1,0 a 1,1 .. x 2 , N
a N /2 aN
2−1 ,1 .. x N
2−1 , N
2−1 ] =( [T]βγ)τ
Show that is linear if g1, g2 ∈W ¿ and C ∈ F theneach v ∈V
T**(ag1+Ψ(v) = (ag1 + Ψ)(T(v)) = ag1(T(v)) + Ψ(T(v))
= aT*(g1)(v) + T*(Ψ)(v) = (aT*(g1) + T*(Ψ)(v)
Let β = {v1,…vn}, γ = {w1….wm}, β* = {fv1…fvn}
And γ* = {gw1…gwn}
[T]βγ = (aij) , then recall from the lemma that for any f ∈V ¿ we have
F = f(v1)fv1 + ….+ f(vn)fvn
The coefficient of fv1 for T*(gwk) is
T*(gwk)(Vi) = gwk(T(Vi)) = gwk(a1,iw1 + ….am,iwm) = ak,i
This is the kth column of [T* ]γ*β*
.