Linear Algebra Homework Solution: Questions on Linear Algebra Concepts
VerifiedAdded on 2021/11/05
|11
|2286
|385
Homework Assignment
AI Summary
This document presents a complete solution to a linear algebra assignment, addressing several key concepts. The solution begins with determining the basis for the span of vectors in two sets using MATLAB code, employing the rref function. It then proceeds to find the basis for the row and column spaces of a matrix, along with its rank. The assignment further explores the nullspace of several matrices, including Hilbert and Pascal matrices, using the null function in MATLAB. The solution also involves finding coordinate matrices with respect to a non-standard basis and solving linear systems. Finally, the assignment concludes by determining change-of-basis matrices for different vector spaces in both R^3 and R^4, using the rref function to transform matrices and the inv function to find inverse matrices.
TABLE OF CONTENTS
QUESTION 6.........................................................................................................................................1
QUESTION 7.........................................................................................................................................2
QUESTION 8.........................................................................................................................................3
QUESTION 9.........................................................................................................................................7
QUESTION 10.......................................................................................................................................7
PRELIMINARY SECTION
... MATLAB EXERCISES
... LINEAR ALGEBRA
clear;
close all;
clc;
QUESTION 6
disp('-------------------------------------------------------------------')
disp('Question 6')
%set #1
sa=[1,2,-1,0];
sb=[-3,-6,3,0];
sc=[-2,-2,1,-1];
disp('Question6: Set (a)')
s1=[sa;sb;sc] %The first set
% finding the subset that forms a basis for the span of the vectors
R1=rref(s1) %determine the linearly independent vectors
disp('The vector that forms the basis for the span of the vectors: ')
v_span=R1(1,:)
%set #
sd=[0,0,1,1,0];
se=[1,1,0,0,1];
sf=[1,1,1,1,1];
sg=[1,1,2,2,1];
sh=[0,0,3,3,1];
sk=[0,0,0,0,1];
disp('Question6: Set (b)')
s2=[sd;se;sf;sg;sh;sk]
% finding the subset that forms a basis for the span of the vectors
R2=rref(s2)
disp('The vector that forms the basis for the span of the vectors: ')
v_span2=R2(3,:)
-------------------------------------------------------------------
Question 6
Question6: Set (a)
s1 =
1
QUESTION 6.........................................................................................................................................1
QUESTION 7.........................................................................................................................................2
QUESTION 8.........................................................................................................................................3
QUESTION 9.........................................................................................................................................7
QUESTION 10.......................................................................................................................................7
PRELIMINARY SECTION
... MATLAB EXERCISES
... LINEAR ALGEBRA
clear;
close all;
clc;
QUESTION 6
disp('-------------------------------------------------------------------')
disp('Question 6')
%set #1
sa=[1,2,-1,0];
sb=[-3,-6,3,0];
sc=[-2,-2,1,-1];
disp('Question6: Set (a)')
s1=[sa;sb;sc] %The first set
% finding the subset that forms a basis for the span of the vectors
R1=rref(s1) %determine the linearly independent vectors
disp('The vector that forms the basis for the span of the vectors: ')
v_span=R1(1,:)
%set #
sd=[0,0,1,1,0];
se=[1,1,0,0,1];
sf=[1,1,1,1,1];
sg=[1,1,2,2,1];
sh=[0,0,3,3,1];
sk=[0,0,0,0,1];
disp('Question6: Set (b)')
s2=[sd;se;sf;sg;sh;sk]
% finding the subset that forms a basis for the span of the vectors
R2=rref(s2)
disp('The vector that forms the basis for the span of the vectors: ')
v_span2=R2(3,:)
-------------------------------------------------------------------
Question 6
Question6: Set (a)
s1 =
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1 2 -1 0
-3 -6 3 0
-2 -2 1 -1
R1 =
1.0000 0 0 1.0000
0 1.0000 -0.5000 -0.5000
0 0 0 0
The vector that forms the basis for the span of the vectors:
v_span =
1 0 0 1
Question6: Set (b)
s2 =
0 0 1 1 0
1 1 0 0 1
1 1 1 1 1
1 1 2 2 1
0 0 3 3 1
0 0 0 0 1
R2 =
1 1 0 0 0
0 0 1 1 0
0 0 0 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
The vector that forms the basis for the span of the vectors:
v_span2 =
0 0 0 0 1
2
-3 -6 3 0
-2 -2 1 -1
R1 =
1.0000 0 0 1.0000
0 1.0000 -0.5000 -0.5000
0 0 0 0
The vector that forms the basis for the span of the vectors:
v_span =
1 0 0 1
Question6: Set (b)
s2 =
0 0 1 1 0
1 1 0 0 1
1 1 1 1 1
1 1 2 2 1
0 0 3 3 1
0 0 0 0 1
R2 =
1 1 0 0 0
0 0 1 1 0
0 0 0 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
The vector that forms the basis for the span of the vectors:
v_span2 =
0 0 0 0 1
2
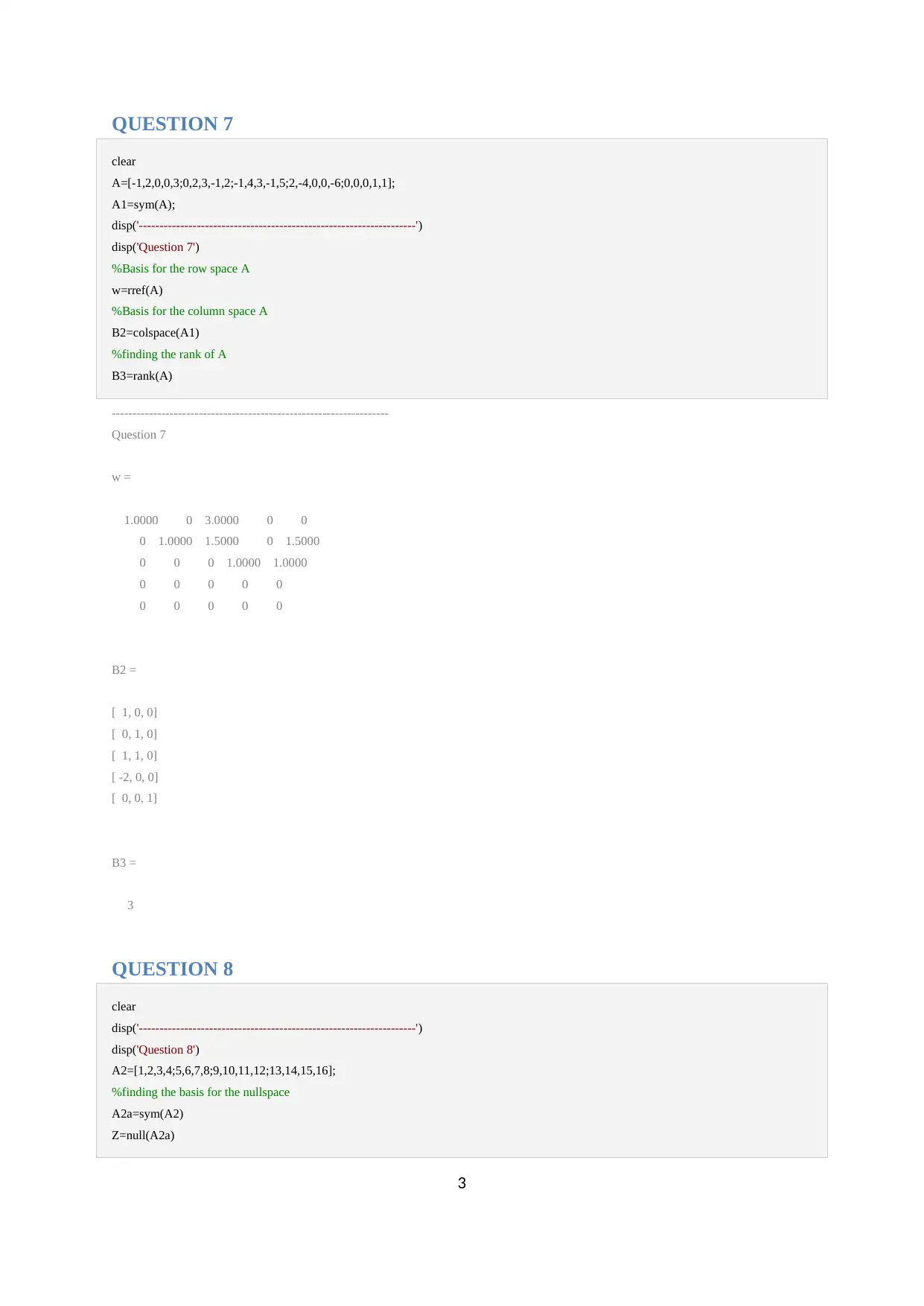
QUESTION 7
clear
A=[-1,2,0,0,3;0,2,3,-1,2;-1,4,3,-1,5;2,-4,0,0,-6;0,0,0,1,1];
A1=sym(A);
disp('-------------------------------------------------------------------')
disp('Question 7')
%Basis for the row space A
w=rref(A)
%Basis for the column space A
B2=colspace(A1)
%finding the rank of A
B3=rank(A)
-------------------------------------------------------------------
Question 7
w =
1.0000 0 3.0000 0 0
0 1.0000 1.5000 0 1.5000
0 0 0 1.0000 1.0000
0 0 0 0 0
0 0 0 0 0
B2 =
[ 1, 0, 0]
[ 0, 1, 0]
[ 1, 1, 0]
[ -2, 0, 0]
[ 0, 0, 1]
B3 =
3
QUESTION 8
clear
disp('-------------------------------------------------------------------')
disp('Question 8')
A2=[1,2,3,4;5,6,7,8;9,10,11,12;13,14,15,16];
%finding the basis for the nullspace
A2a=sym(A2)
Z=null(A2a)
3
clear
A=[-1,2,0,0,3;0,2,3,-1,2;-1,4,3,-1,5;2,-4,0,0,-6;0,0,0,1,1];
A1=sym(A);
disp('-------------------------------------------------------------------')
disp('Question 7')
%Basis for the row space A
w=rref(A)
%Basis for the column space A
B2=colspace(A1)
%finding the rank of A
B3=rank(A)
-------------------------------------------------------------------
Question 7
w =
1.0000 0 3.0000 0 0
0 1.0000 1.5000 0 1.5000
0 0 0 1.0000 1.0000
0 0 0 0 0
0 0 0 0 0
B2 =
[ 1, 0, 0]
[ 0, 1, 0]
[ 1, 1, 0]
[ -2, 0, 0]
[ 0, 0, 1]
B3 =
3
QUESTION 8
clear
disp('-------------------------------------------------------------------')
disp('Question 8')
A2=[1,2,3,4;5,6,7,8;9,10,11,12;13,14,15,16];
%finding the basis for the nullspace
A2a=sym(A2)
Z=null(A2a)
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
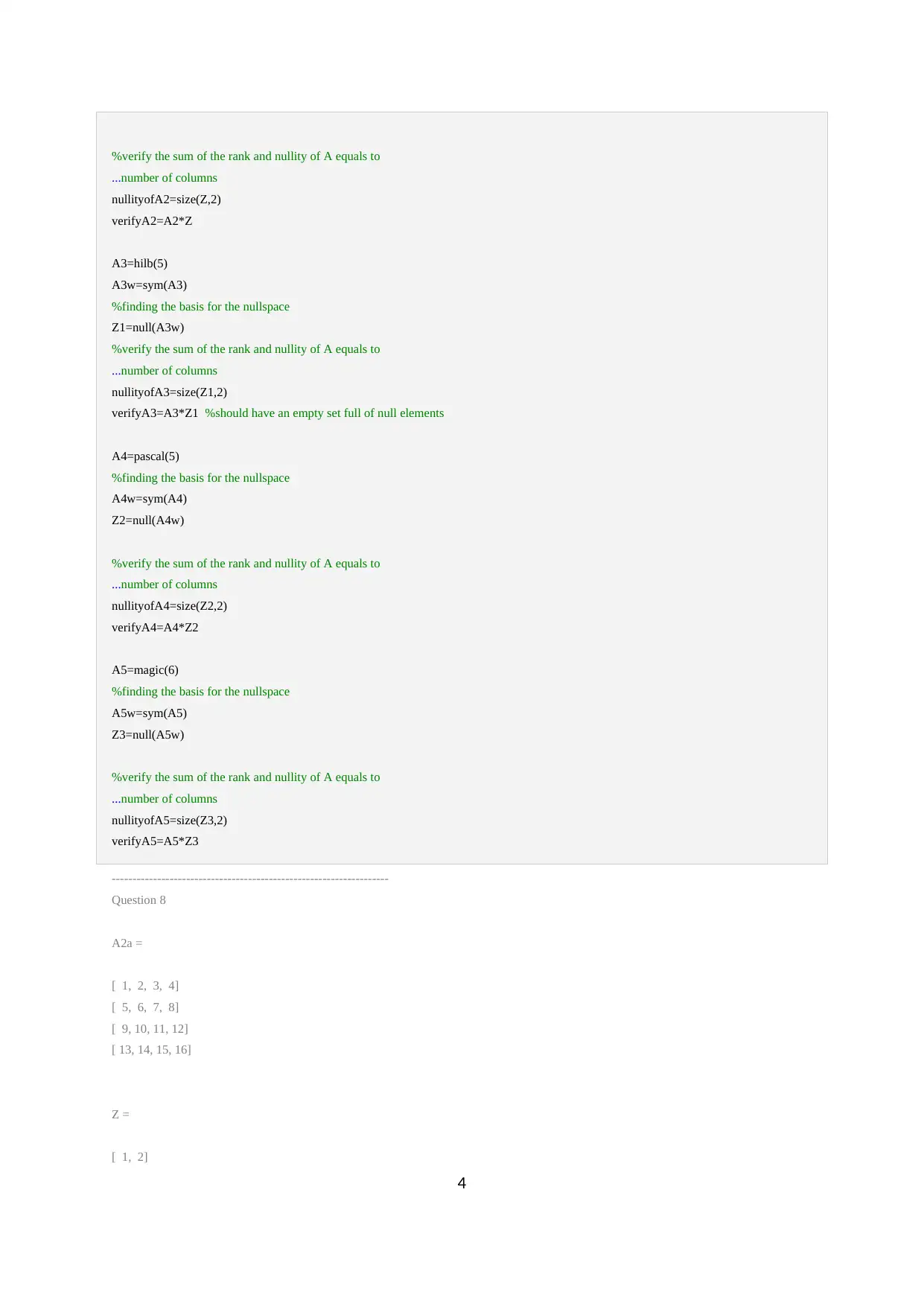
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA2=size(Z,2)
verifyA2=A2*Z
A3=hilb(5)
A3w=sym(A3)
%finding the basis for the nullspace
Z1=null(A3w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA3=size(Z1,2)
verifyA3=A3*Z1 %should have an empty set full of null elements
A4=pascal(5)
%finding the basis for the nullspace
A4w=sym(A4)
Z2=null(A4w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA4=size(Z2,2)
verifyA4=A4*Z2
A5=magic(6)
%finding the basis for the nullspace
A5w=sym(A5)
Z3=null(A5w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA5=size(Z3,2)
verifyA5=A5*Z3
-------------------------------------------------------------------
Question 8
A2a =
[ 1, 2, 3, 4]
[ 5, 6, 7, 8]
[ 9, 10, 11, 12]
[ 13, 14, 15, 16]
Z =
[ 1, 2]
4
...number of columns
nullityofA2=size(Z,2)
verifyA2=A2*Z
A3=hilb(5)
A3w=sym(A3)
%finding the basis for the nullspace
Z1=null(A3w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA3=size(Z1,2)
verifyA3=A3*Z1 %should have an empty set full of null elements
A4=pascal(5)
%finding the basis for the nullspace
A4w=sym(A4)
Z2=null(A4w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA4=size(Z2,2)
verifyA4=A4*Z2
A5=magic(6)
%finding the basis for the nullspace
A5w=sym(A5)
Z3=null(A5w)
%verify the sum of the rank and nullity of A equals to
...number of columns
nullityofA5=size(Z3,2)
verifyA5=A5*Z3
-------------------------------------------------------------------
Question 8
A2a =
[ 1, 2, 3, 4]
[ 5, 6, 7, 8]
[ 9, 10, 11, 12]
[ 13, 14, 15, 16]
Z =
[ 1, 2]
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

[ -2, -3]
[ 1, 0]
[ 0, 1]
nullityofA2 =
2
verifyA2 =
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
A3 =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
A3w =
[ 1, 1/2, 1/3, 1/4, 1/5]
[ 1/2, 1/3, 1/4, 1/5, 1/6]
[ 1/3, 1/4, 1/5, 1/6, 1/7]
[ 1/4, 1/5, 1/6, 1/7, 1/8]
[ 1/5, 1/6, 1/7, 1/8, 1/9]
Z1 =
Empty sym: 1-by-0
nullityofA3 =
0
verifyA3 =
[ [], [], [], [], []]
5
[ 1, 0]
[ 0, 1]
nullityofA2 =
2
verifyA2 =
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
A3 =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
A3w =
[ 1, 1/2, 1/3, 1/4, 1/5]
[ 1/2, 1/3, 1/4, 1/5, 1/6]
[ 1/3, 1/4, 1/5, 1/6, 1/7]
[ 1/4, 1/5, 1/6, 1/7, 1/8]
[ 1/5, 1/6, 1/7, 1/8, 1/9]
Z1 =
Empty sym: 1-by-0
nullityofA3 =
0
verifyA3 =
[ [], [], [], [], []]
5

[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
A4 =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
A4w =
[ 1, 1, 1, 1, 1]
[ 1, 2, 3, 4, 5]
[ 1, 3, 6, 10, 15]
[ 1, 4, 10, 20, 35]
[ 1, 5, 15, 35, 70]
Z2 =
Empty sym: 1-by-0
nullityofA4 =
0
verifyA4 =
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
A5 =
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
6
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
A4 =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
A4w =
[ 1, 1, 1, 1, 1]
[ 1, 2, 3, 4, 5]
[ 1, 3, 6, 10, 15]
[ 1, 4, 10, 20, 35]
[ 1, 5, 15, 35, 70]
Z2 =
Empty sym: 1-by-0
nullityofA4 =
0
verifyA4 =
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
[ [], [], [], [], []]
A5 =
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

30 5 34 12 14 16
4 36 29 13 18 11
A5w =
[ 35, 1, 6, 26, 19, 24]
[ 3, 32, 7, 21, 23, 25]
[ 31, 9, 2, 22, 27, 20]
[ 8, 28, 33, 17, 10, 15]
[ 30, 5, 34, 12, 14, 16]
[ 4, 36, 29, 13, 18, 11]
Z3 =
2
2
-1
-2
-2
1
nullityofA5 =
1
verifyA5 =
0
0
0
0
0
0
QUESTION 9
clear
disp('-------------------------------------------------------------------')
disp('Question 9')
q1=[1,0,1];
q2=[0,-1,2];
q3=[2,3,-5];
Q=[q1;q2;q3]; %non-standard basis for R^3
7
4 36 29 13 18 11
A5w =
[ 35, 1, 6, 26, 19, 24]
[ 3, 32, 7, 21, 23, 25]
[ 31, 9, 2, 22, 27, 20]
[ 8, 28, 33, 17, 10, 15]
[ 30, 5, 34, 12, 14, 16]
[ 4, 36, 29, 13, 18, 11]
Z3 =
2
2
-1
-2
-2
1
nullityofA5 =
1
verifyA5 =
0
0
0
0
0
0
QUESTION 9
clear
disp('-------------------------------------------------------------------')
disp('Question 9')
q1=[1,0,1];
q2=[0,-1,2];
q3=[2,3,-5];
Q=[q1;q2;q3]; %non-standard basis for R^3
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
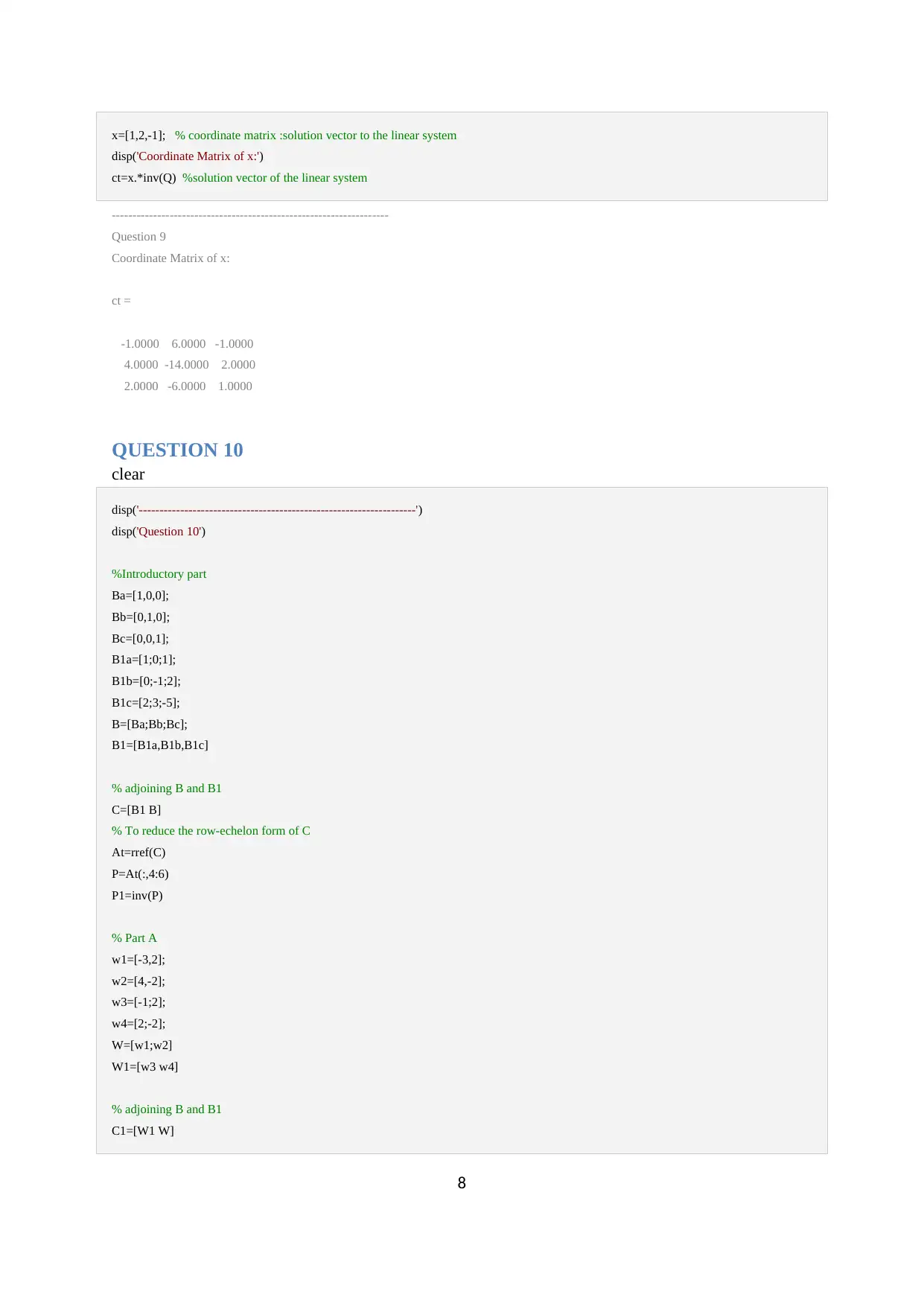
x=[1,2,-1]; % coordinate matrix :solution vector to the linear system
disp('Coordinate Matrix of x:')
ct=x.*inv(Q) %solution vector of the linear system
-------------------------------------------------------------------
Question 9
Coordinate Matrix of x:
ct =
-1.0000 6.0000 -1.0000
4.0000 -14.0000 2.0000
2.0000 -6.0000 1.0000
QUESTION 10
clear
disp('-------------------------------------------------------------------')
disp('Question 10')
%Introductory part
Ba=[1,0,0];
Bb=[0,1,0];
Bc=[0,0,1];
B1a=[1;0;1];
B1b=[0;-1;2];
B1c=[2;3;-5];
B=[Ba;Bb;Bc];
B1=[B1a,B1b,B1c]
% adjoining B and B1
C=[B1 B]
% To reduce the row-echelon form of C
At=rref(C)
P=At(:,4:6)
P1=inv(P)
% Part A
w1=[-3,2];
w2=[4,-2];
w3=[-1;2];
w4=[2;-2];
W=[w1;w2]
W1=[w3 w4]
% adjoining B and B1
C1=[W1 W]
8
disp('Coordinate Matrix of x:')
ct=x.*inv(Q) %solution vector of the linear system
-------------------------------------------------------------------
Question 9
Coordinate Matrix of x:
ct =
-1.0000 6.0000 -1.0000
4.0000 -14.0000 2.0000
2.0000 -6.0000 1.0000
QUESTION 10
clear
disp('-------------------------------------------------------------------')
disp('Question 10')
%Introductory part
Ba=[1,0,0];
Bb=[0,1,0];
Bc=[0,0,1];
B1a=[1;0;1];
B1b=[0;-1;2];
B1c=[2;3;-5];
B=[Ba;Bb;Bc];
B1=[B1a,B1b,B1c]
% adjoining B and B1
C=[B1 B]
% To reduce the row-echelon form of C
At=rref(C)
P=At(:,4:6)
P1=inv(P)
% Part A
w1=[-3,2];
w2=[4,-2];
w3=[-1;2];
w4=[2;-2];
W=[w1;w2]
W1=[w3 w4]
% adjoining B and B1
C1=[W1 W]
8

% To reduce the row-echelon form of C
At1=rref(C1)
Pa=At1(:,3:4)
Pa1=inv(Pa) %inverting the Pa matrix using the inv function
% Part B
Bx=[[1,1,1,1];[0,1,1,1];[0,0,1,1];[0,0,0,1]]
Bx1=[[1;0;1;0],[1;0;-1;0],[0;1;0;1],[0;1;0;-1]]
% adjoining B and B1
C2=[Bx1 Bx]
% To reduce the row-echelon form of C
At2=rref(C2)
Pb=At2(:,5:8)
Pb1=inv(Pb)
-------------------------------------------------------------------
Question 10
B1 =
1 0 2
0 -1 3
1 2 -5
C =
1 0 2 1 0 0
0 -1 3 0 1 0
1 2 -5 0 0 1
At =
1 0 0 -1 4 2
0 1 0 3 -7 -3
0 0 1 1 -2 -1
P =
-1 4 2
3 -7 -3
1 -2 -1
P1 =
1.0000 0.0000 2.0000
9
At1=rref(C1)
Pa=At1(:,3:4)
Pa1=inv(Pa) %inverting the Pa matrix using the inv function
% Part B
Bx=[[1,1,1,1];[0,1,1,1];[0,0,1,1];[0,0,0,1]]
Bx1=[[1;0;1;0],[1;0;-1;0],[0;1;0;1],[0;1;0;-1]]
% adjoining B and B1
C2=[Bx1 Bx]
% To reduce the row-echelon form of C
At2=rref(C2)
Pb=At2(:,5:8)
Pb1=inv(Pb)
-------------------------------------------------------------------
Question 10
B1 =
1 0 2
0 -1 3
1 2 -5
C =
1 0 2 1 0 0
0 -1 3 0 1 0
1 2 -5 0 0 1
At =
1 0 0 -1 4 2
0 1 0 3 -7 -3
0 0 1 1 -2 -1
P =
-1 4 2
3 -7 -3
1 -2 -1
P1 =
1.0000 0.0000 2.0000
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

0 -1.0000 3.0000
1.0000 2.0000 -5.0000
W =
-3 2
4 -2
W1 =
-1 2
2 -2
C1 =
-1 2 -3 2
2 -2 4 -2
At1 =
1 0 1 0
0 1 -1 1
Pa =
1 0
-1 1
Pa1 =
1 0
1 1
Bx =
1 1 1 1
0 1 1 1
0 0 1 1
0 0 0 1
Bx1 =
10
1.0000 2.0000 -5.0000
W =
-3 2
4 -2
W1 =
-1 2
2 -2
C1 =
-1 2 -3 2
2 -2 4 -2
At1 =
1 0 1 0
0 1 -1 1
Pa =
1 0
-1 1
Pa1 =
1 0
1 1
Bx =
1 1 1 1
0 1 1 1
0 0 1 1
0 0 0 1
Bx1 =
10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1 1 0 0
0 0 1 1
1 -1 0 0
0 0 1 -1
C2 =
1 1 0 0 1 1 1 1
0 0 1 1 0 1 1 1
1 -1 0 0 0 0 1 1
0 0 1 -1 0 0 0 1
At2 =
Columns 1 through 7
1.0000 0 0 0 0.5000 0.5000 1.0000
0 1.0000 0 0 0.5000 0.5000 0
0 0 1.0000 0 0 0.5000 0.5000
0 0 0 1.0000 0 0.5000 0.5000
Column 8
1.0000
0
1.0000
0
Pb =
0.5000 0.5000 1.0000 1.0000
0.5000 0.5000 0 0
0 0.5000 0.5000 1.0000
0 0.5000 0.5000 0
Pb1 =
1 1 -1 -1
-1 1 1 1
1 -1 -1 1
0 0 1 -1
11
0 0 1 1
1 -1 0 0
0 0 1 -1
C2 =
1 1 0 0 1 1 1 1
0 0 1 1 0 1 1 1
1 -1 0 0 0 0 1 1
0 0 1 -1 0 0 0 1
At2 =
Columns 1 through 7
1.0000 0 0 0 0.5000 0.5000 1.0000
0 1.0000 0 0 0.5000 0.5000 0
0 0 1.0000 0 0 0.5000 0.5000
0 0 0 1.0000 0 0.5000 0.5000
Column 8
1.0000
0
1.0000
0
Pb =
0.5000 0.5000 1.0000 1.0000
0.5000 0.5000 0 0
0 0.5000 0.5000 1.0000
0 0.5000 0.5000 0
Pb1 =
1 1 -1 -1
-1 1 1 1
1 -1 -1 1
0 0 1 -1
11
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

