Maths Assignment - Linear Equations and Applications, University
VerifiedAdded on 2022/09/02
|18
|2080
|34
Homework Assignment
AI Summary
This comprehensive maths assignment solution covers various aspects of linear equations. The solution starts with finding intercepts and graphing linear equations. It then delves into word problems involving cost analysis, revenue, and break-even points, including scenarios about car rentals, sales of different units, and hourly wages. The document also includes problems related to calculating prices of goods and creating linear equations from given data, such as determining the cost of t-shirts with graphics. Finally, the solution analyzes a manufacturing scenario, determining the break-even point by comparing cost and revenue equations. The student has provided step-by-step solutions including graphical representations and algebraic manipulations to arrive at final answers. The assignment covers a wide array of mathematical concepts related to linear equations and their practical applications.

Running head: MATHS
MATHS
Name of the Student
Name of the University
Author Note
MATHS
Name of the Student
Name of the University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
MATHS
Activity 10:
Part A:
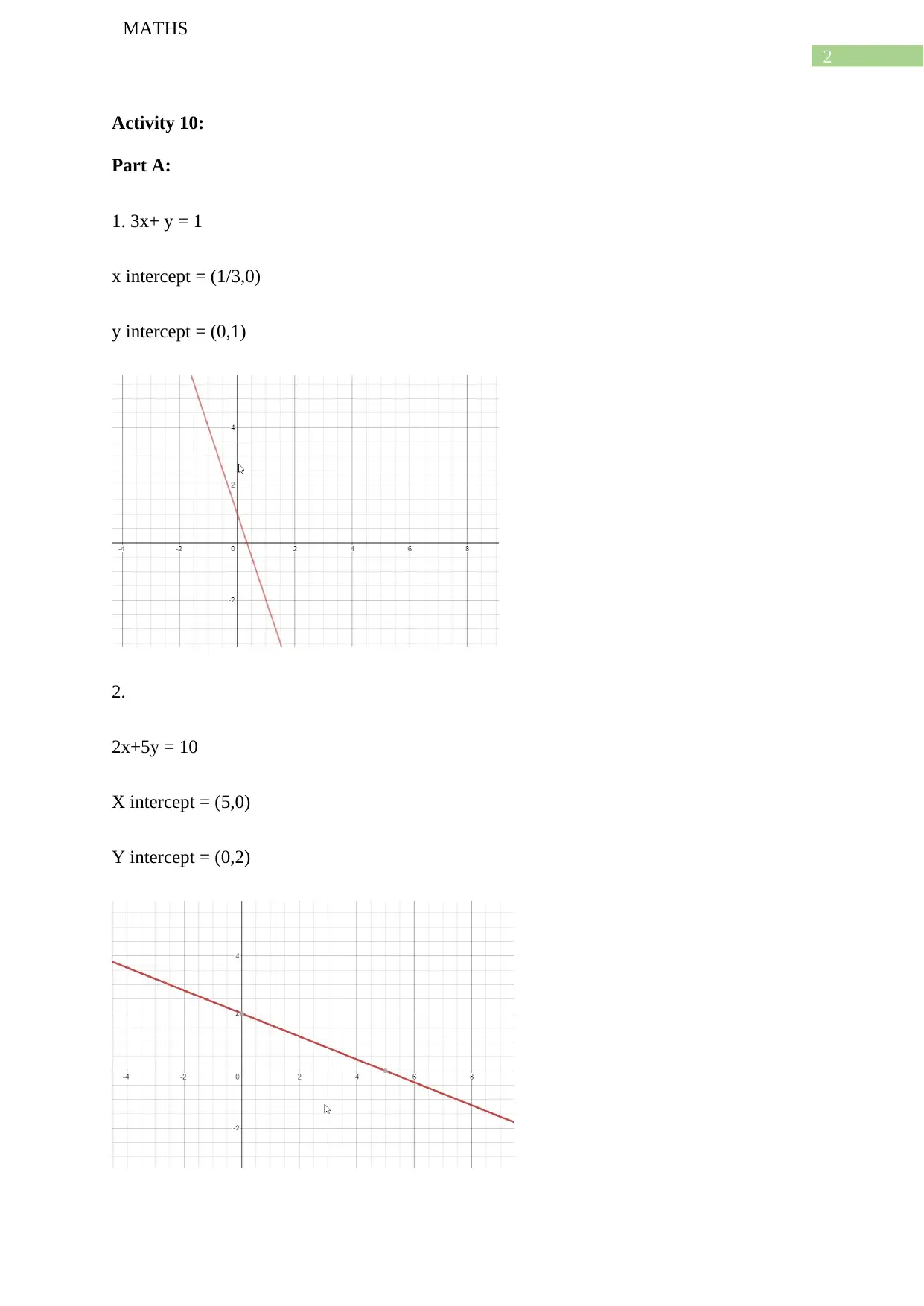
1. 3x+ y = 1
x intercept = (1/3,0)
y intercept = (0,1)
2.
2x+5y = 10
X intercept = (5,0)
Y intercept = (0,2)
MATHS
Activity 10:
Part A:
1. 3x+ y = 1
x intercept = (1/3,0)
y intercept = (0,1)
2.
2x+5y = 10
X intercept = (5,0)
Y intercept = (0,2)
3
MATHS
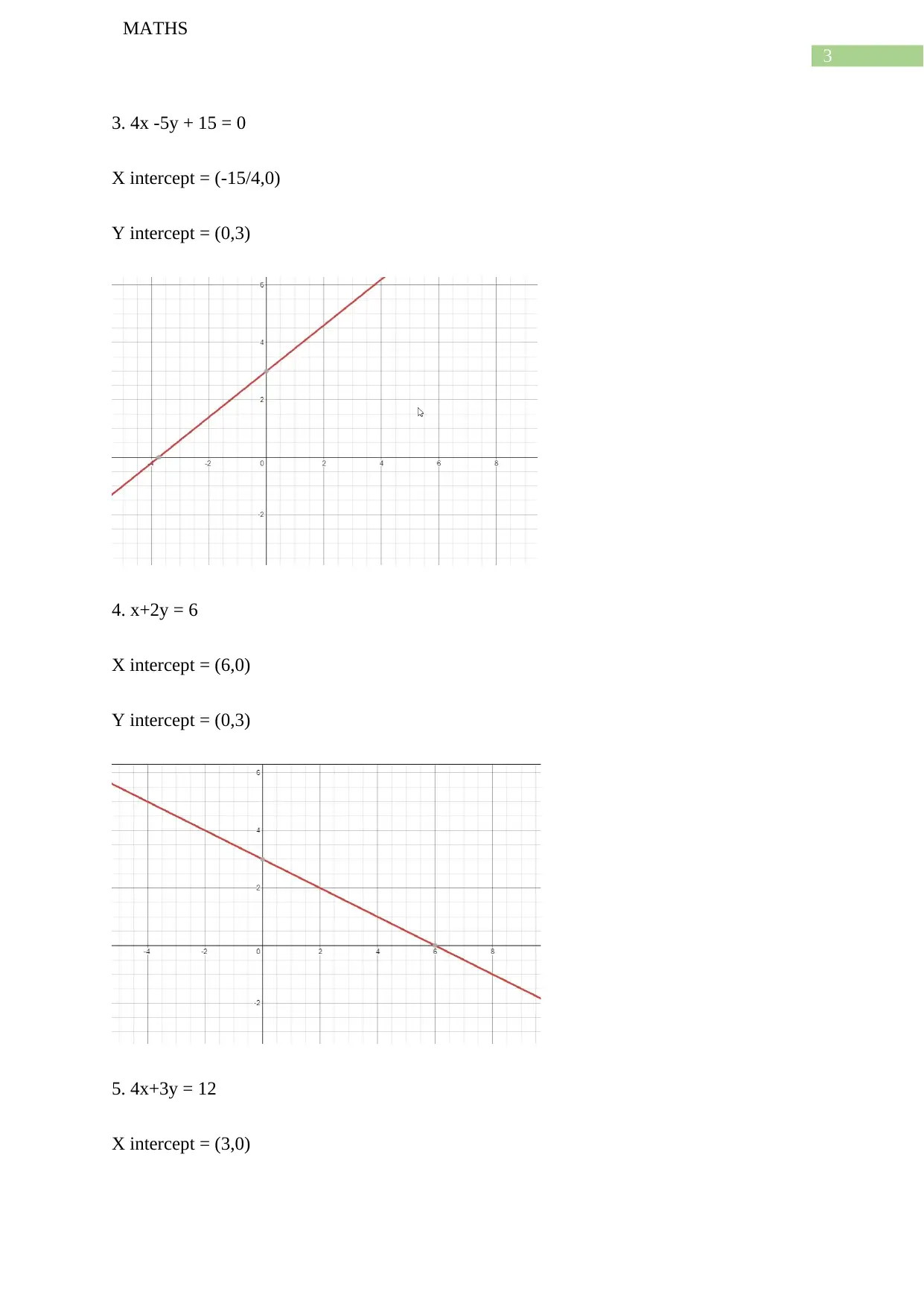
3. 4x -5y + 15 = 0
X intercept = (-15/4,0)
Y intercept = (0,3)
4. x+2y = 6
X intercept = (6,0)
Y intercept = (0,3)
5. 4x+3y = 12
X intercept = (3,0)
MATHS
3. 4x -5y + 15 = 0
X intercept = (-15/4,0)
Y intercept = (0,3)
4. x+2y = 6
X intercept = (6,0)
Y intercept = (0,3)
5. 4x+3y = 12
X intercept = (3,0)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
4
MATHS
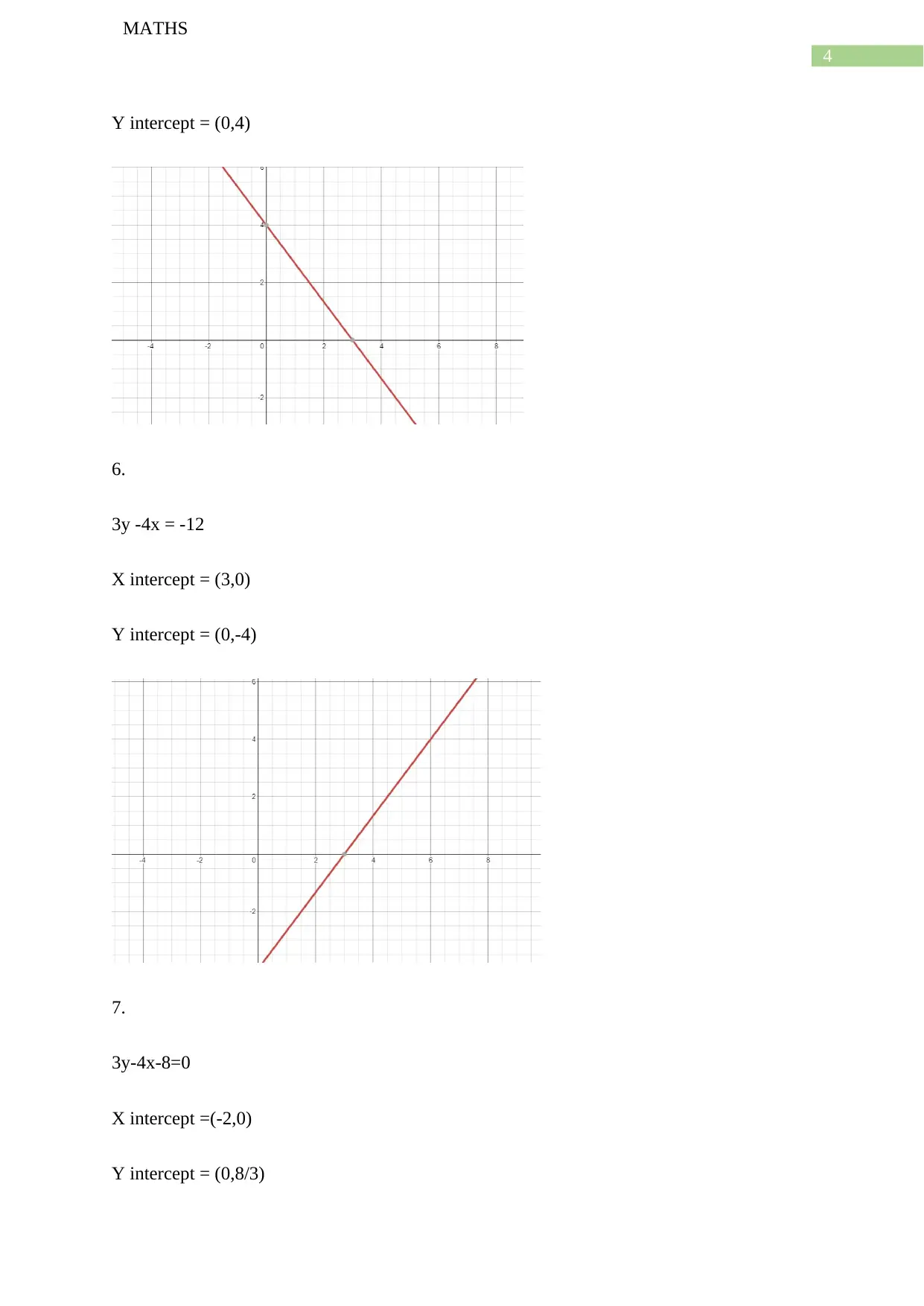
Y intercept = (0,4)
6.
3y -4x = -12
X intercept = (3,0)
Y intercept = (0,-4)
7.
3y-4x-8=0
X intercept =(-2,0)
Y intercept = (0,8/3)
MATHS
Y intercept = (0,4)
6.
3y -4x = -12
X intercept = (3,0)
Y intercept = (0,-4)
7.
3y-4x-8=0
X intercept =(-2,0)
Y intercept = (0,8/3)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5
MATHS
Part B:
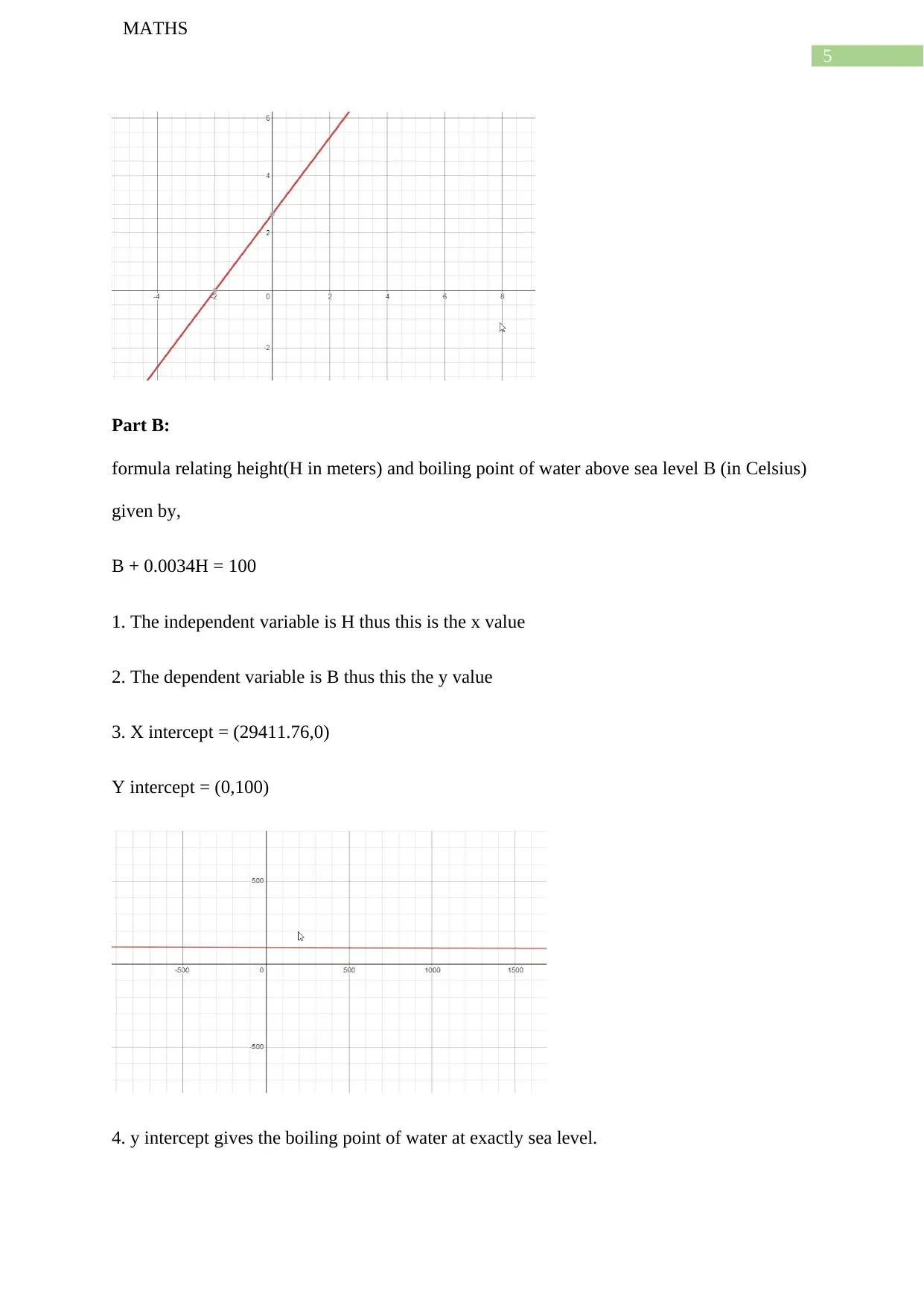
formula relating height(H in meters) and boiling point of water above sea level B (in Celsius)
given by,
B + 0.0034H = 100
1. The independent variable is H thus this is the x value
2. The dependent variable is B thus this the y value
3. X intercept = (29411.76,0)
Y intercept = (0,100)
4. y intercept gives the boiling point of water at exactly sea level.
MATHS
Part B:
formula relating height(H in meters) and boiling point of water above sea level B (in Celsius)
given by,
B + 0.0034H = 100
1. The independent variable is H thus this is the x value
2. The dependent variable is B thus this the y value
3. X intercept = (29411.76,0)
Y intercept = (0,100)
4. y intercept gives the boiling point of water at exactly sea level.

6
MATHS
5. 0.0034 is the increment in Boiling point temperature in Celsius for a meter increase in
height.
Activity 11:
In the above figure it is somehow difficult to find the y intercepts as lines are crossing each
other. Hence, for finding the equation of the line a different technique can be applied. The
end points of the lines can easily be determined as they starts and ends with a whole number
of grid points. Thus after determining start and end point let (x1,y1) and (x2,y2) the equation
of a line can be determined by the following equation
(y-y1) = (x-x1)*(y2-y1)/(x2-x1) (point slope form of straight line)
Similarly using the above equation the equations of all the straight lines can be determined.
Activity 12:
Let the two other companies from which Chad could rent a car are Supercars and Car-times.
The breakdown of total costs of Supercars is $35 fixed initial charge and $0.50 per kilometre
charge.
The breakdown of total cost of Car-times is $40 fixed initial charge and $0.40 per kilometre
charge.
MATHS
5. 0.0034 is the increment in Boiling point temperature in Celsius for a meter increase in
height.
Activity 11:
In the above figure it is somehow difficult to find the y intercepts as lines are crossing each
other. Hence, for finding the equation of the line a different technique can be applied. The
end points of the lines can easily be determined as they starts and ends with a whole number
of grid points. Thus after determining start and end point let (x1,y1) and (x2,y2) the equation
of a line can be determined by the following equation
(y-y1) = (x-x1)*(y2-y1)/(x2-x1) (point slope form of straight line)
Similarly using the above equation the equations of all the straight lines can be determined.
Activity 12:
Let the two other companies from which Chad could rent a car are Supercars and Car-times.
The breakdown of total costs of Supercars is $35 fixed initial charge and $0.50 per kilometre
charge.
The breakdown of total cost of Car-times is $40 fixed initial charge and $0.40 per kilometre
charge.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
MATHS
Flyer for Supercars:
Flyer for Car-times:
SuperCars
Rent a car at amazing price
Car-times
MATHS
Flyer for Supercars:
Flyer for Car-times:
SuperCars
Rent a car at amazing price
Car-times
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
MATHS
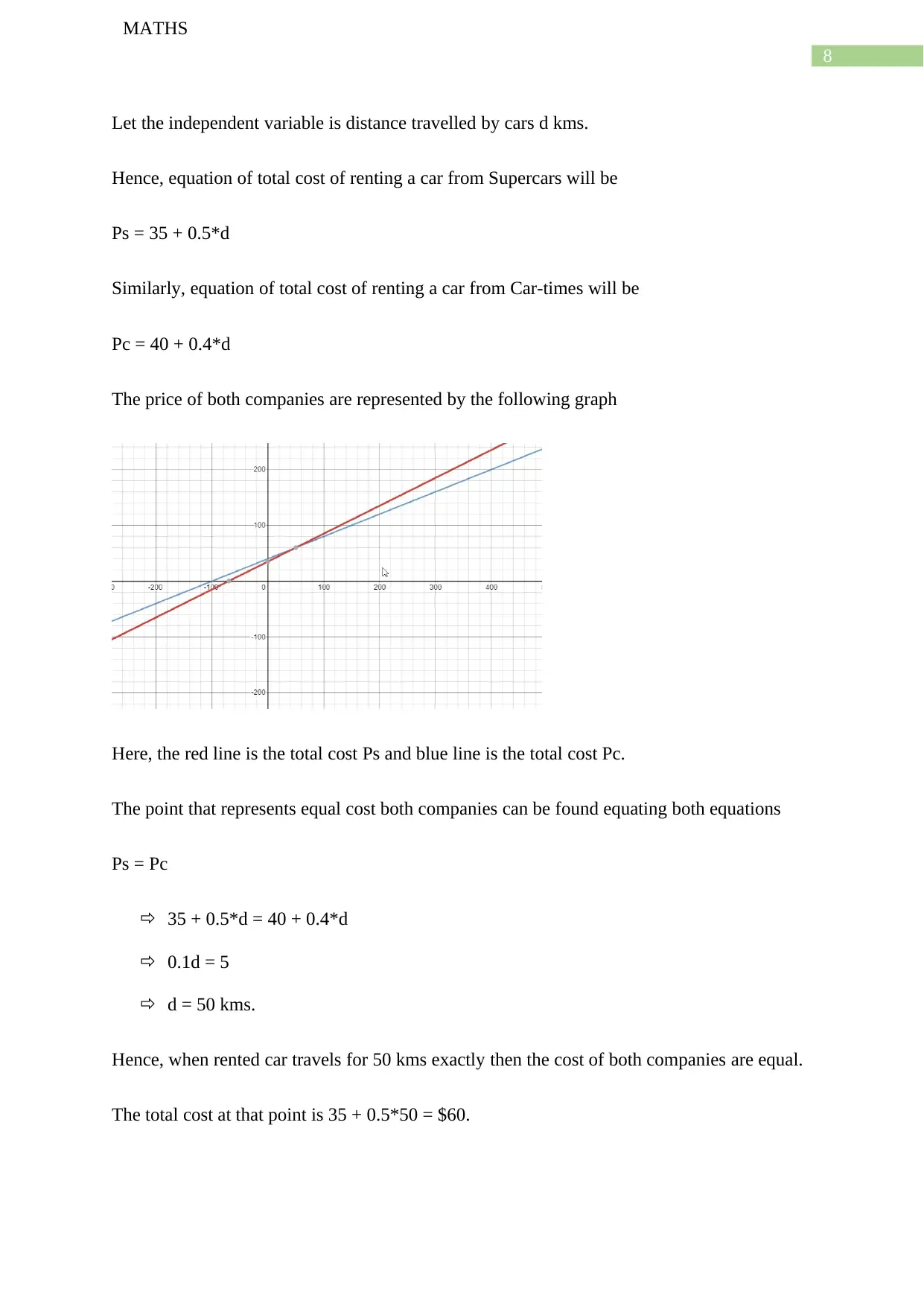
Let the independent variable is distance travelled by cars d kms.
Hence, equation of total cost of renting a car from Supercars will be
Ps = 35 + 0.5*d
Similarly, equation of total cost of renting a car from Car-times will be
Pc = 40 + 0.4*d
The price of both companies are represented by the following graph
Here, the red line is the total cost Ps and blue line is the total cost Pc.
The point that represents equal cost both companies can be found equating both equations
Ps = Pc
35 + 0.5*d = 40 + 0.4*d
0.1d = 5
d = 50 kms.
Hence, when rented car travels for 50 kms exactly then the cost of both companies are equal.
The total cost at that point is 35 + 0.5*50 = $60.
MATHS
Let the independent variable is distance travelled by cars d kms.
Hence, equation of total cost of renting a car from Supercars will be
Ps = 35 + 0.5*d
Similarly, equation of total cost of renting a car from Car-times will be
Pc = 40 + 0.4*d
The price of both companies are represented by the following graph
Here, the red line is the total cost Ps and blue line is the total cost Pc.
The point that represents equal cost both companies can be found equating both equations
Ps = Pc
35 + 0.5*d = 40 + 0.4*d
0.1d = 5
d = 50 kms.
Hence, when rented car travels for 50 kms exactly then the cost of both companies are equal.
The total cost at that point is 35 + 0.5*50 = $60.

9
MATHS
Hence, for Chad it will benefitted to use car from Supercars if he travels less than 50 kms or
if he travels over 50 kms then it will be benefitted to use Car-times service and he can use
either one if he wants to travel exactly 50 kms with same cost.
Activity 13:
Standard units sold s = 5
Deluxe unit sold d= 4
Total selling price = $39000
In next month standard units sold s = 4
Deluxe unit sold d = 2
Total selling price = $24000
1. Equation to represent first month’s sales
5s + 4d = 39000 (1)
2. Equation to represent second month’s sales
4s + 2d = 24000 (2)
Now, solving (1) and (2) by substitution method
4d = 39000 – 5s => 2d = (39000 – 5s)/2
Substituting in (2) gives
4s + (39000 – 5s)/2 = 24000
8s + 39000 – 5s = 48000
3s = 9000
s = $3000
MATHS
Hence, for Chad it will benefitted to use car from Supercars if he travels less than 50 kms or
if he travels over 50 kms then it will be benefitted to use Car-times service and he can use
either one if he wants to travel exactly 50 kms with same cost.
Activity 13:
Standard units sold s = 5
Deluxe unit sold d= 4
Total selling price = $39000
In next month standard units sold s = 4
Deluxe unit sold d = 2
Total selling price = $24000
1. Equation to represent first month’s sales
5s + 4d = 39000 (1)
2. Equation to represent second month’s sales
4s + 2d = 24000 (2)
Now, solving (1) and (2) by substitution method
4d = 39000 – 5s => 2d = (39000 – 5s)/2
Substituting in (2) gives
4s + (39000 – 5s)/2 = 24000
8s + 39000 – 5s = 48000
3s = 9000
s = $3000
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

10
MATHS
Hence, 2d = (39000-5*3000)/2 = 12000
d = $6000
3. Hence, standard units are sold for $3000
4. Deluxe units are sold for $6000
Activity 14:
1. Let hourly rate = $h per hour and overtime rate = $o per hour.
Hence, for first week total 14.5 hours worked.
Hence, 10*h + 4.5*o = 93.75 (1)
In the second week total 12 hours worked.
Hence, 10*h + 2*o = 75 (2)
Thus, 10h = 93.75 – 4.5o from (1)
And, 10h = 75 – 2o from (2)
Hence, 93.75 – 4.5o = 75-2o
2.5o = 18.75
o = $7.5 per hour
Hence, h = (93.75 – 4.5*7.5)/10 = $6 per hour.
Hence, hourly wage of Cathy is $6 per hour and overtime wage of Cathy is $7.5 per hour.
2.
Let jeans price = j
Blouse price = b
MATHS
Hence, 2d = (39000-5*3000)/2 = 12000
d = $6000
3. Hence, standard units are sold for $3000
4. Deluxe units are sold for $6000
Activity 14:
1. Let hourly rate = $h per hour and overtime rate = $o per hour.
Hence, for first week total 14.5 hours worked.
Hence, 10*h + 4.5*o = 93.75 (1)
In the second week total 12 hours worked.
Hence, 10*h + 2*o = 75 (2)
Thus, 10h = 93.75 – 4.5o from (1)
And, 10h = 75 – 2o from (2)
Hence, 93.75 – 4.5o = 75-2o
2.5o = 18.75
o = $7.5 per hour
Hence, h = (93.75 – 4.5*7.5)/10 = $6 per hour.
Hence, hourly wage of Cathy is $6 per hour and overtime wage of Cathy is $7.5 per hour.
2.
Let jeans price = j
Blouse price = b
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

11
MATHS
Hence, by Cathy’s bill
3b + 2j = 57 (1)
And, by Brenda’s bill
4b + 3j = 81 (2)
Multiplying (1) by 3 and (2) by 2 and then subtracting (1) from (2) gives
9b + 6j = 171
-8b - 6j = -162
=> b = $9
Hence, j = (57-3*9)/2 = $15
Hence, price of a blouse is $9 and price of a pair of jeans is $15.
3.
Let cost of hamburger = $h
Let cost of French fries = $f
Hence, the system of linear equation will be
8h + 5f = 24 (1)
6h + 2f = 16.60 (2)
Multiplying (1) by 2 and (2) by 5 and then subtracting gives
16h + 10f = 48
-30h - 10f = -83
=> -14h = -35
MATHS
Hence, by Cathy’s bill
3b + 2j = 57 (1)
And, by Brenda’s bill
4b + 3j = 81 (2)
Multiplying (1) by 3 and (2) by 2 and then subtracting (1) from (2) gives
9b + 6j = 171
-8b - 6j = -162
=> b = $9
Hence, j = (57-3*9)/2 = $15
Hence, price of a blouse is $9 and price of a pair of jeans is $15.
3.
Let cost of hamburger = $h
Let cost of French fries = $f
Hence, the system of linear equation will be
8h + 5f = 24 (1)
6h + 2f = 16.60 (2)
Multiplying (1) by 2 and (2) by 5 and then subtracting gives
16h + 10f = 48
-30h - 10f = -83
=> -14h = -35

12
MATHS
=> h = $2.5
Hence, f = (24-8*2.5)/5 = $0.8
Hence, price of a hamburger is $2.5 and price of a French fry is $0.8.
Activity 15:
Given, initial cost of manufacture = $20000
Per unit game manufacture cost after initial cost = $4 per unit
Wholesale price = $15 per game
Part A:
1.
The total cost of manufacturing any number of games is equal to $20000 added with per unit
cost multiplied by number of units.
2. Rewriting equation with x as independent and y as dependent variable
y = 20000+ 4x (1)
y = total cost of manufacturing
x = number of units manufactured
3. The revenue of any number of games sold is $15 multiplied with number of games sold.
4. Rewriting equation with x as independent and y as dependent variable
y = 15x (2)
y = revenue
x = number of units sold
MATHS
=> h = $2.5
Hence, f = (24-8*2.5)/5 = $0.8
Hence, price of a hamburger is $2.5 and price of a French fry is $0.8.
Activity 15:
Given, initial cost of manufacture = $20000
Per unit game manufacture cost after initial cost = $4 per unit
Wholesale price = $15 per game
Part A:
1.
The total cost of manufacturing any number of games is equal to $20000 added with per unit
cost multiplied by number of units.
2. Rewriting equation with x as independent and y as dependent variable
y = 20000+ 4x (1)
y = total cost of manufacturing
x = number of units manufactured
3. The revenue of any number of games sold is $15 multiplied with number of games sold.
4. Rewriting equation with x as independent and y as dependent variable
y = 15x (2)
y = revenue
x = number of units sold
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 18
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


