Linear Optimization Assignment: Solver and Sensitivity Reports

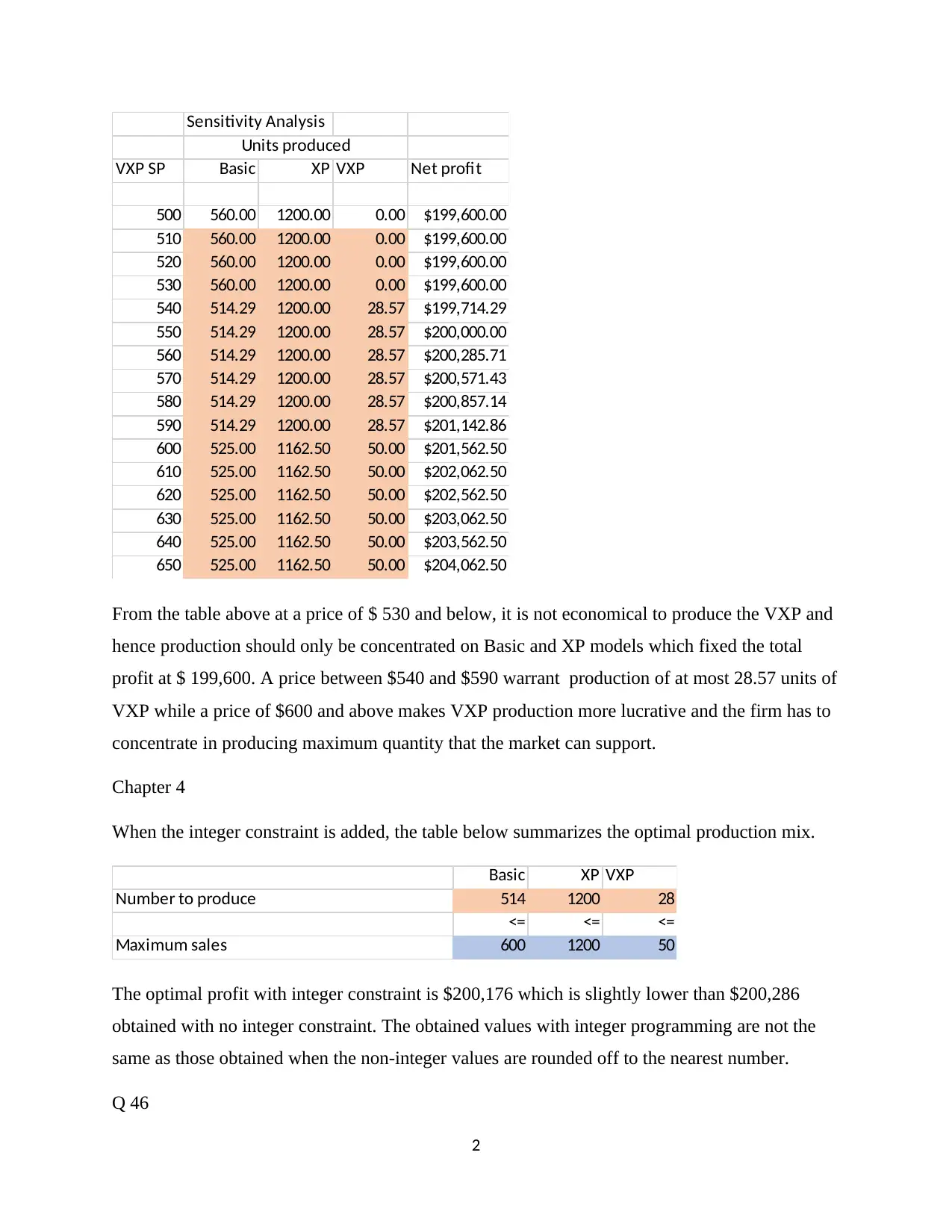
This document provides solutions to a linear optimization assignment. It covers problems from Chapters 3 and 4, including a product mix problem for PC Tech with the introduction of a VXP model, requiring the use of Solver and sensitivity analysis. The assignment explores optimal production levels, profitability, and the impact of price variations. Integer programming is also applied to obtain feasible solutions. Additionally, the document includes solutions for a Smalltown police officer scheduling problem, and a furniture company's production optimization problem, analyzing labor hours and wood supply constraints. Finally, it addresses a farm management problem involving corn and wheat production, with a focus on meeting requirements at minimal cost and analyzing the sensitivity of production levels. The solutions involve interpreting Solver's Answer and Sensitivity Reports, providing insights into key results and optimal strategies.

Linear Optimization
Student Name
Institution
Date
Chapter 3
Q 2
a. Optimal product mix
When the new model VXP is introduced to the production mix, the optimal production
level obtained is indicated in the table below.
Basic XP VXP
Number to produce 514.2857143 1200 28.57143
<= <= <=
Maximum sales 600 1200 50
This give an optimal profitability of $200,286.
b. When the values are rounded off to the nearest integers, the solution obtained is not
feasible. For instance, the total hours used for both assembling and testing exceeds the
hours available for the same. To obtain a feasible solution that is at least closer to the
optimal solution, Integer programming should be used instead. This entails adding the
integer constrains for the number of units to be produced.
Q 3
The table summaries how the variation of the VXP prices will affect the optimal production mix
and the total profit.
1

Sensitivity Analysis
VXP SP Basic XP VXP Net profit
500 560.00 1200.00 0.00 $199,600.00
510 560.00 1200.00 0.00 $199,600.00
520 560.00 1200.00 0.00 $199,600.00
530 560.00 1200.00 0.00 $199,600.00
540 514.29 1200.00 28.57 $199,714.29
550 514.29 1200.00 28.57 $200,000.00
560 514.29 1200.00 28.57 $200,285.71
570 514.29 1200.00 28.57 $200,571.43
580 514.29 1200.00 28.57 $200,857.14
590 514.29 1200.00 28.57 $201,142.86
600 525.00 1162.50 50.00 $201,562.50
610 525.00 1162.50 50.00 $202,062.50
620 525.00 1162.50 50.00 $202,562.50
630 525.00 1162.50 50.00 $203,062.50
640 525.00 1162.50 50.00 $203,562.50
650 525.00 1162.50 50.00 $204,062.50
Units produced
From the table above at a price of $ 530 and below, it is not economical to produce the VXP and
hence production should only be concentrated on Basic and XP models which fixed the total
profit at $ 199,600. A price between $540 and $590 warrant production of at most 28.57 units of
VXP while a price of $600 and above makes VXP production more lucrative and the firm has to
concentrate in producing maximum quantity that the market can support.
Chapter 4
When the integer constraint is added, the table below summarizes the optimal production mix.
Basic XP VXP
Number to produce 514 1200 28
<= <= <=
Maximum sales 600 1200 50
The optimal profit with integer constraint is $200,176 which is slightly lower than $200,286
obtained with no integer constraint. The obtained values with integer programming are not the
same as those obtained when the non-integer values are rounded off to the nearest number.
Q 46
2

a. To meet Smalltown’s daily police need a total of 21 police officers should be employed
by the police force. The officers shift should be scheduled as presented in the table
below.
Police force scheduling
Starting 4 hours of 8-hour shift
M-4A 4A-8A 8A-N N-4P 4P-8P 8P-M
Number starting 2 2 5 2 6 4
Number available each
4-hour period 6 4 7 7 8 10
>= >= >= >= >= >=
Number required 4 4 7 7 8 10
Total employed 21
Q 58
a. From the answer report, the two constraints that is labor hours valuable and the total
supply of units of wood are not binding. This means that their supply is limited and
the firm has to maximize the available quantities for an optimal production. To
maximize the profit of the furniture company, the firm need to produce the units of
chairs and tables according to the specifications described in the table below.
Table Chair
Total numbers to produce 142.0 930.0
Number finished 142 929
Number sold unfinished 0 1
This will maximize the derived profits at $ 185,309.
Q 67
a. The constraint to be met is that the total planting space for each of the farms is 100
hectares and the production capacity for corn have to be equal to or above 7000 bushels
and that one for wheat has to be equal to or exceed 11,000 bushels. So as to meet the
requirements at a minimal cost the farm manager should grow wheat in 27.5 hectares of
3

farm 1 and grow corn in 10.77 hectares of farm 2. This will optimize the cost of
production to $3,767. The table summarizes the details.
Acres to plant Farm 1 Farm 2 Yield
Corn 0.00 10.77 7000
Wheat 27.50 0.00 11000
From the sensitivity report the corn production can be increased by up to 58,000 bushels
while the wheat production can be increased by up to 29000 without affecting the optimal
decision.
4