Supply Chain Analysis and Design: Nut Supplier Case Study Analysis

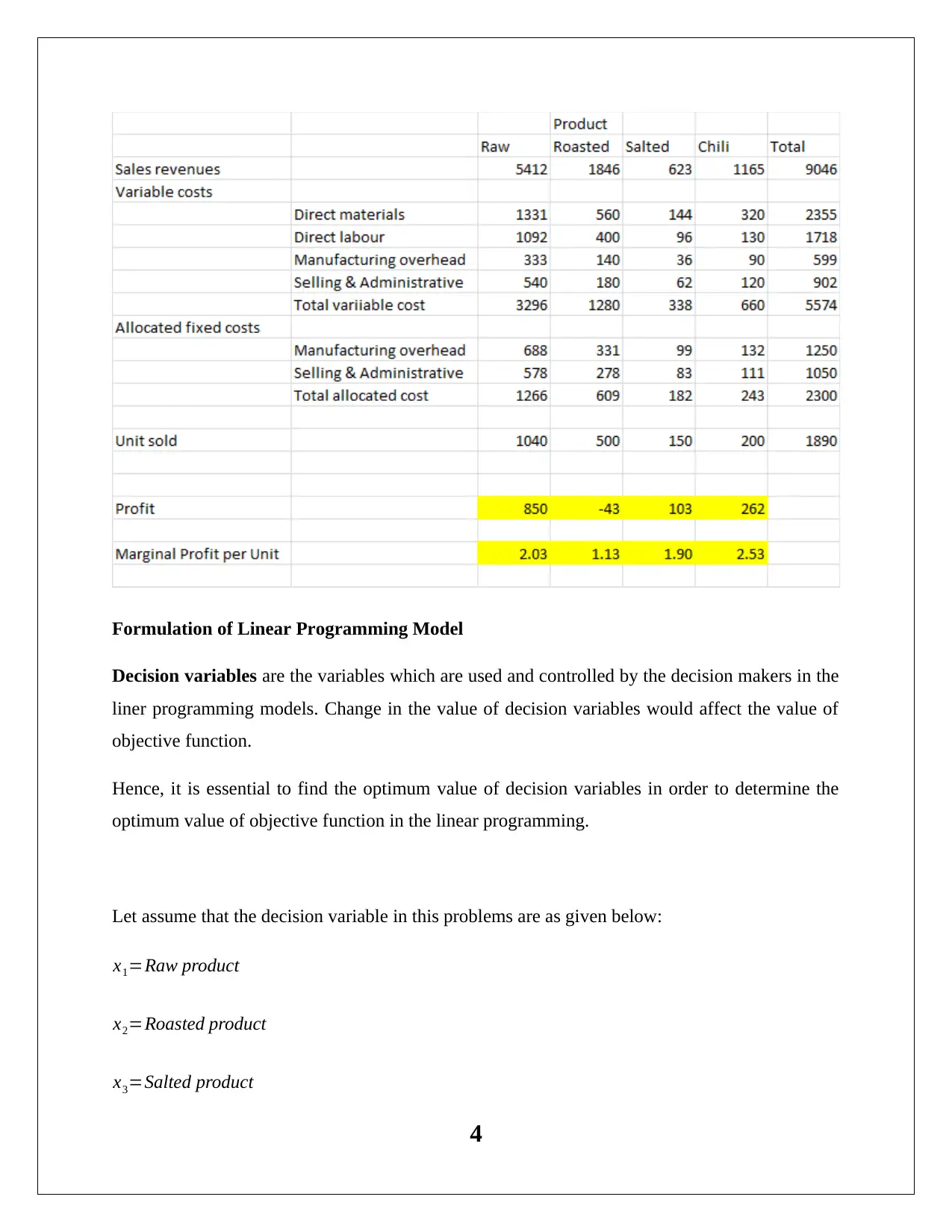
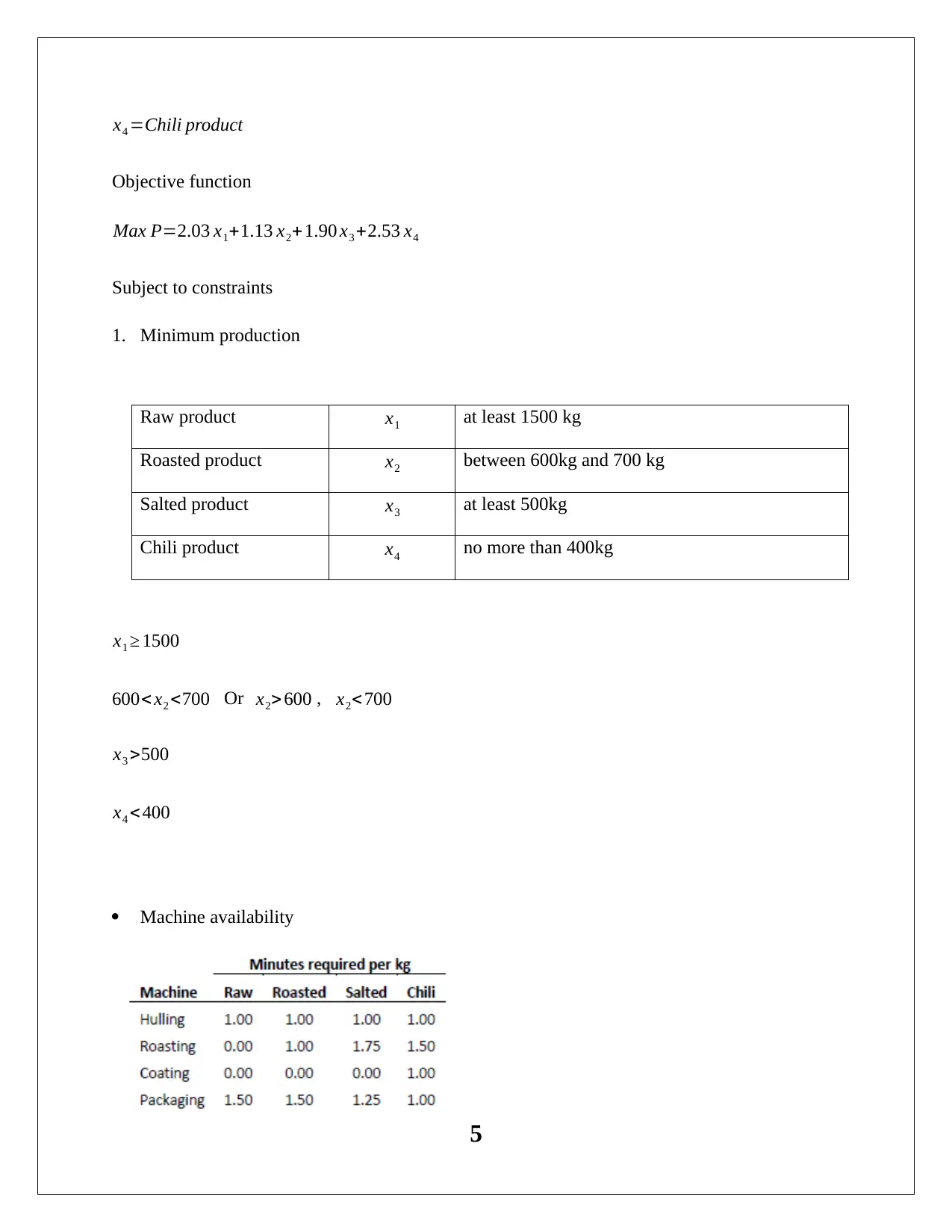
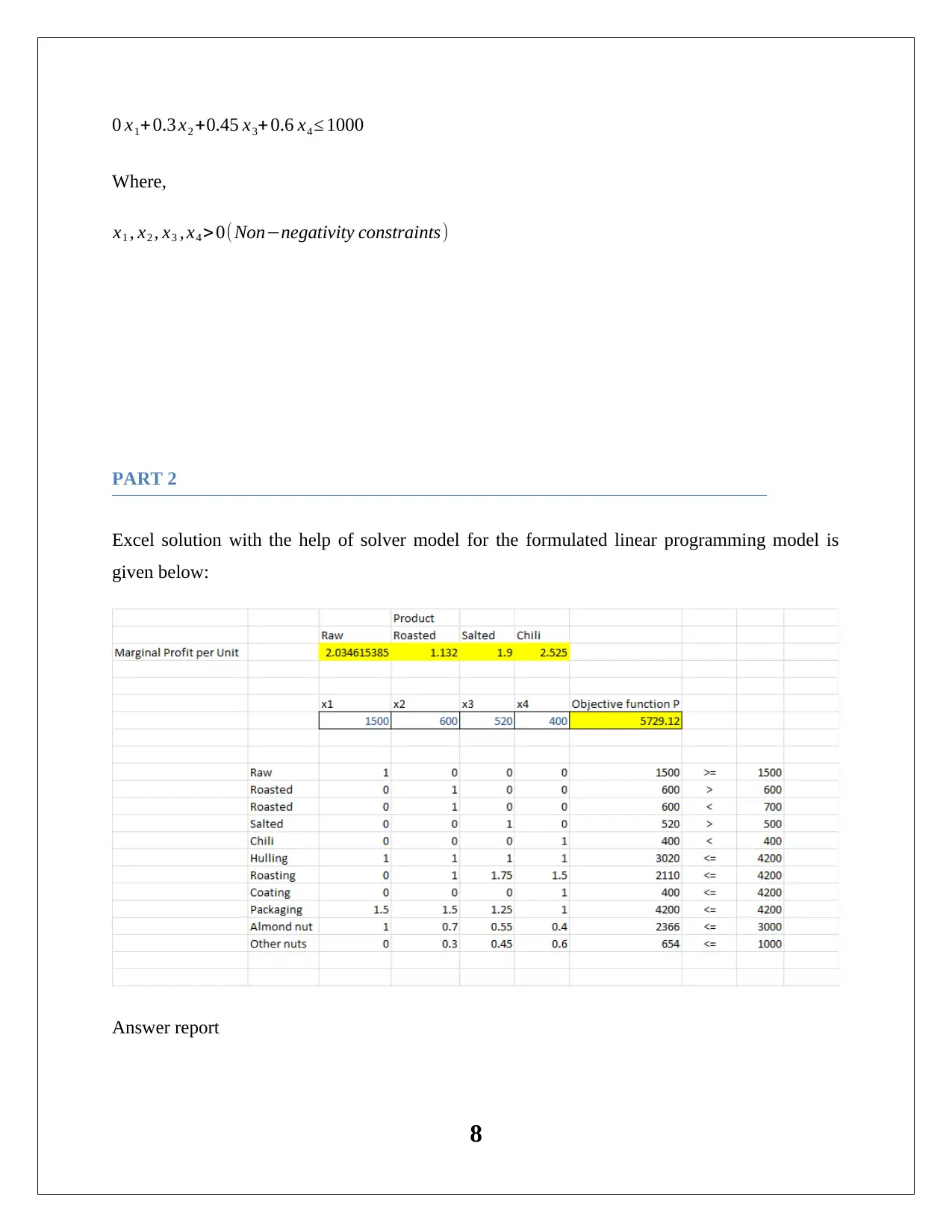
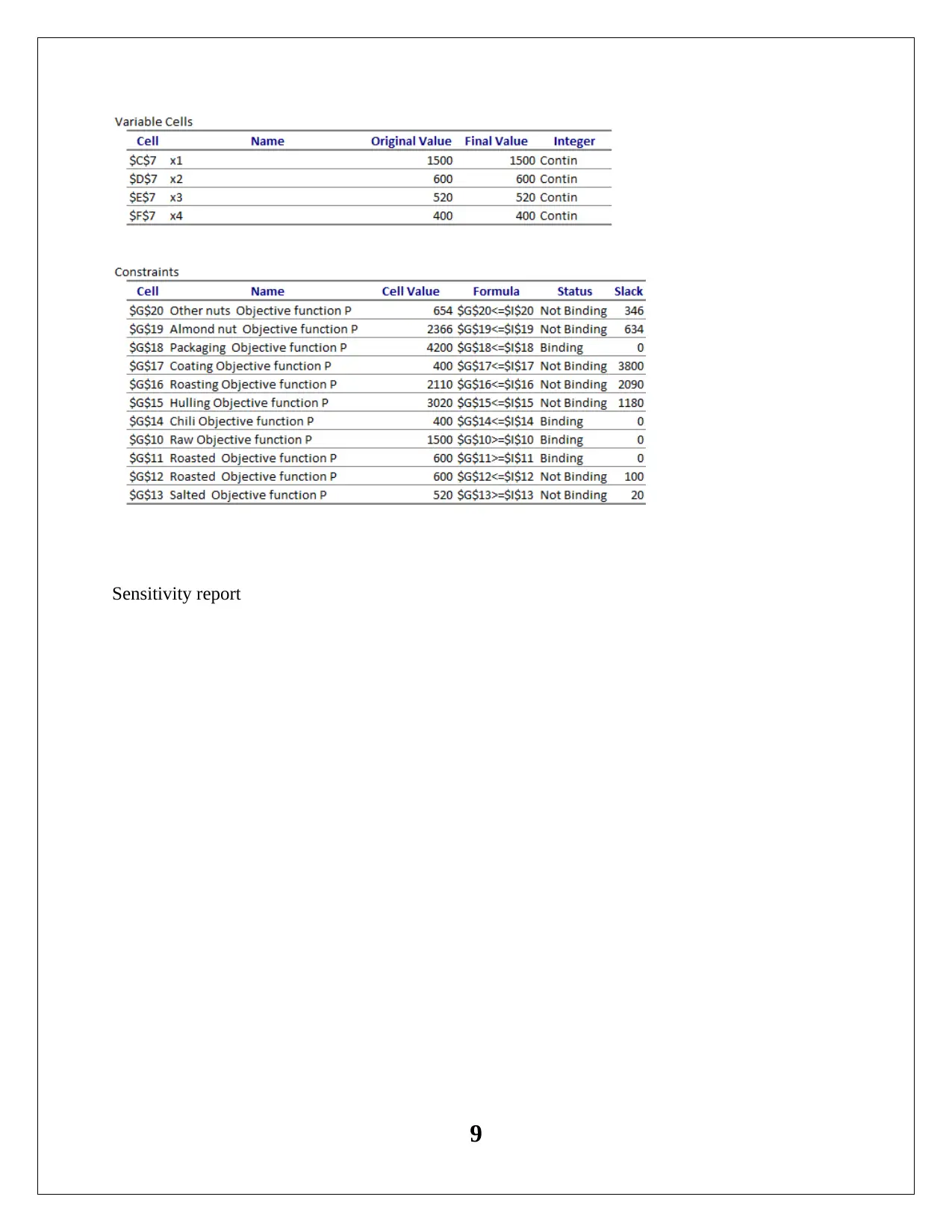
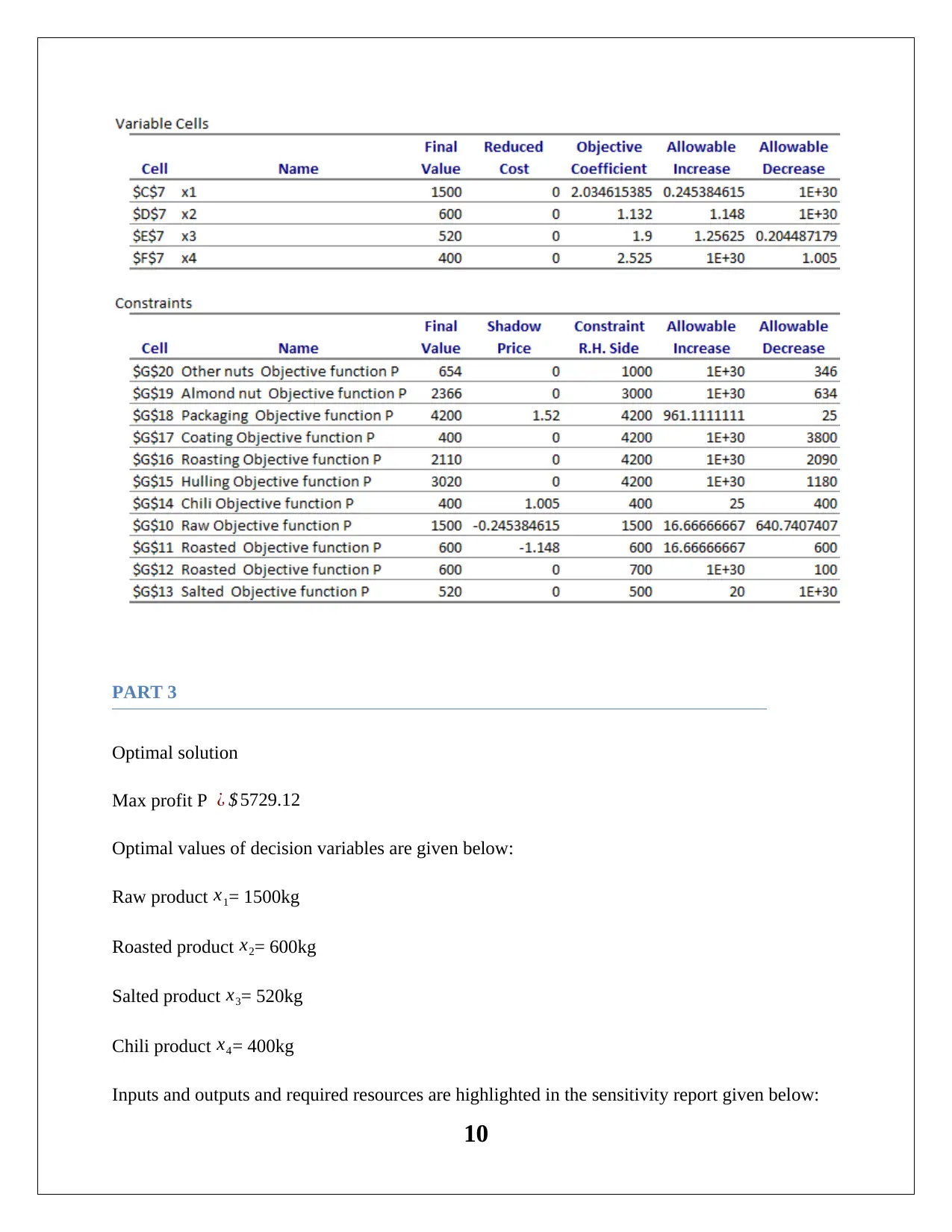
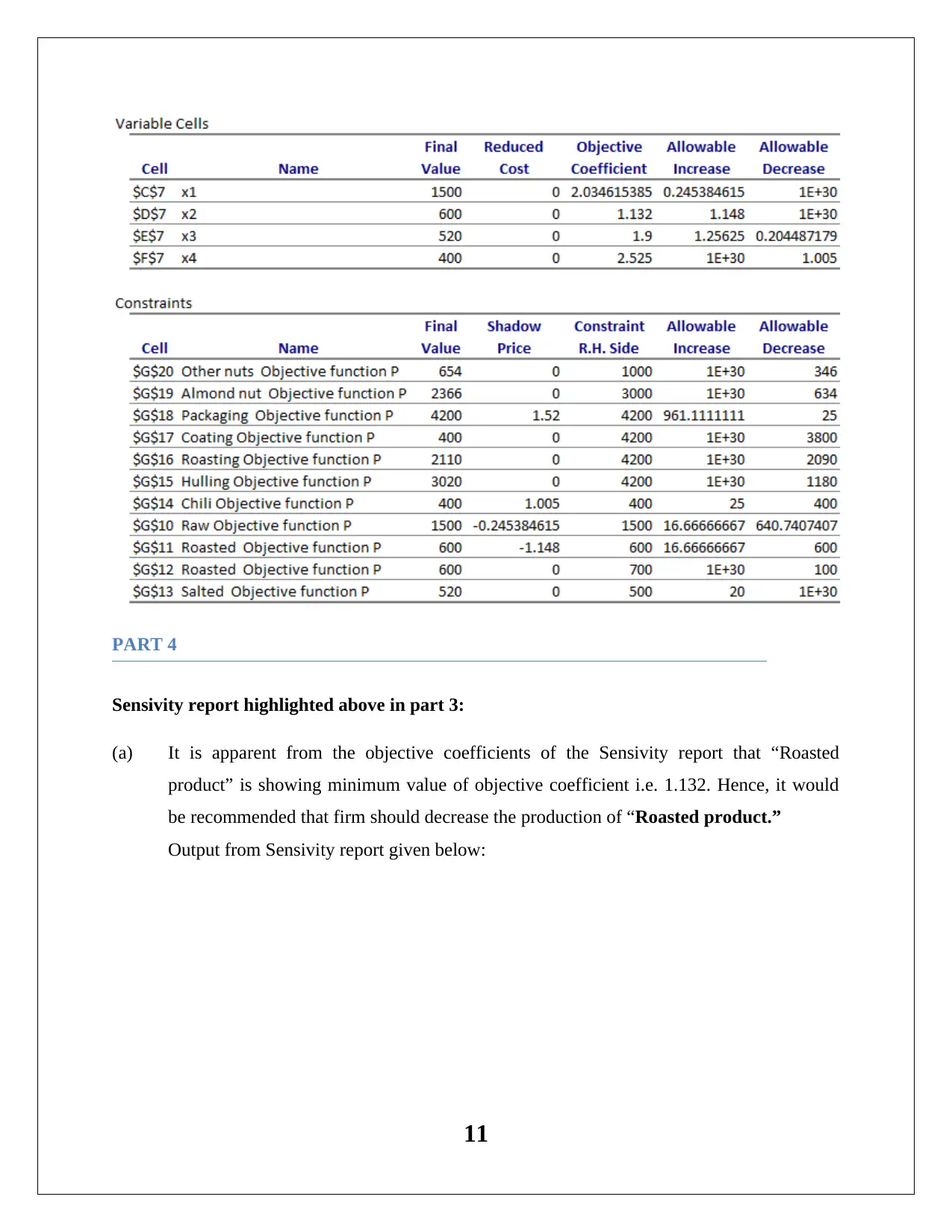
This case study analyzes a nut supplier's operations, focusing on optimizing production and maximizing profit using a linear programming model. The firm produces four nut-based products: Raw, Roasted, Salted, and Chili. The assignment outlines the problem, including production constraints, resource availability (almonds, other nuts, and machine time), and profit margins. A linear programming model is formulated, defining decision variables, an objective function (maximizing total profit), and constraints related to production volumes, nut availability, and machine capacity. The Excel Solver is used to find the optimal solution. The solution provides optimal production quantities for each product, maximizing profit while adhering to constraints. Sensitivity analysis is performed to identify the impact of changes in objective function coefficients and resource availability on the optimal solution. The case study recommends adjustments to production based on the sensitivity report and analyzes the impact of price changes on profitability. The solution highlights the importance of machine utilization and the overall impact of decisions on the firm's financial performance.

SUPPLY CHAIN ANALYSIS AND DESIGN
Case study: Nut Supplier Linear Programming Model
Student id
[Pick the date]

Case study: Nut Supplier
PART 1
The given data and information is summarized below:
A firm is making four different products from nuts in Australia. These products are given below:
 Raw nuts (Raw)
 Roasted mixed nuts (Roasted)
 Roasted and salted mixed nuts (Salted)
 Chill-coated mixed nuts (Chili)
1. Minimum production
 Raw product at least 1500 kg
 Roasted product between 600kg and 700 kg
 Salted product at least 500kg
 Chili product no more than 400kg
2. % of almond present in per kg of product
 Raw product = 100%
 Roasted product = 70%
 Salted product = 55%
 Chili product = 40%
3. % of other nut present in per kg of product (Remaining weight made up of other nuts)
 Raw product = 0%
1

 Roasted product = 30%
 Salted product = 45%
 Chili product = 60%
4. Available quantity of nuts in company which would use in next year
 Almond nuts = 3000kg
 Other nuts = 1000 kg
5. Machines required for the production of products and their working minutes needed per kg of
product
6. Availability of each machine in next week = 70 hours = 4200 min.
7. Financial summary of the firm’s average weekly operations over-past quarter
2

The aim is to maximize the total profit of the firm.
It is essential to determine the marginal profit per unit sold associated with the products.
Profit=Revenue− ( total variable cost +total ¿cost )
Profit per unit= Profit
Units sold
Marginal profit per unit=( Revenue−Total variable cost
Units sold )
3

Formulation of Linear Programming Model
Decision variables are the variables which are used and controlled by the decision makers in the
liner programming models. Change in the value of decision variables would affect the value of
objective function.
Hence, it is essential to find the optimum value of decision variables in order to determine the
optimum value of objective function in the linear programming.
Let assume that the decision variable in this problems are as given below:
x1=Raw product
x2=Roasted product
x3=Salted product
4

x4 =Chili product
Objective function
Max P=2.03 x1+1.13 x2+1.90 x3 +2.53 x4
Subject to constraints
1. Minimum production
Raw product x1 at least 1500 kg
Roasted product x2 between 600kg and 700 kg
Salted product x3 at least 500kg
Chili product x4 no more than 400kg
x1 ≥ 1500
600< x2 <700 Or x2> 600 , x2< 700
x3 >500
x4 <400
 Machine availability
5

Total time = 4200 minutes
x1+ x2 +x3 + x4 ≤ 4200
0 x1+ x2 +1.75 x3+1.50 x4 ≤ 4200
0 x1+0 x2 +0 x3 +x4 ≤ 4200
1.50 x1+1.50 x2+ 1.25 x3 + x4 ≤ 4200
 Amount of nuts
Almond nut
 Raw product x1= 100%
 Roasted product x2= 70%
 Salted product x3= 55%
 Chili product x4= 40%
x1+ 0.7 x2 +0.55 x3 +0.40 x4 ≤ 3000
Other nuts
 Raw product x1= 0%
 Roasted product x2= 30%
 Salted product x3= 45%
 Chili product x4= 60%
0 x1+0.3 x2 +0.45 x3+ 0.6 x4 ≤ 1000
6

Final Linear programming problem
Objective function
Max P=2.03 x1+1.13 x2+1.90 x3 +2.53 x4
Subject to constraints
x1 ≥ 1500
x2> 600
x2< 700
x3 >500
x4 <400
x1+ x2 +x3 + x4 ≤ 4200
0 x1+ x2 +1.75 x3+1.50 x4 ≤ 4200
0 x1+0 x2 +0 x3 +x4 ≤ 4200
1.50 x1+1.50 x2+ 1.25 x3 + x4 ≤ 4200
x1+ 0.7 x2 +0.55 x3 +0.40 x4 ≤ 3000
7

0 x1+0.3 x2 +0.45 x3+ 0.6 x4 ≤ 1000
Where,
x1 , x2 , x3 , x4 > 0(Non−negativity constraints)
PART 2
Excel solution with the help of solver model for the formulated linear programming model is
given below:
Answer report
8

Sensitivity report
9

PART 3
Optimal solution
Max profit P ¿ $ 5729.12
Optimal values of decision variables are given below:
Raw product x1= 1500kg
Roasted product x2= 600kg
Salted product x3= 520kg
Chili product x4= 400kg
Inputs and outputs and required resources are highlighted in the sensitivity report given below:
10

PART 4
Sensivity report highlighted above in part 3:
(a) It is apparent from the objective coefficients of the Sensivity report that “Roasted
product” is showing minimum value of objective coefficient i.e. 1.132. Hence, it would
be recommended that firm should decrease the production of “Roasted product.”
Output from Sensivity report given below:
11