MSC 3371 - Portfolio Optimization: Linear Programming & Sensitivity

This assignment focuses on applying linear programming and sensitivity analysis to optimize a stock portfolio consisting of Petroleum Inc. and Quality Steel shares. The goal is to maximize the total annual return while adhering to constraints related to funds available, risk maximum, and the maximum number of Petroleum Inc. shares. The solution provides the optimal number of shares for each stock, the total annual return, and an analysis of shadow prices for funds available and risk maximum. It also discusses the impact of increasing investments in Petroleum Inc. and the implications of changes in the right-hand side ranges for chopped onions and jalapenos. Furthermore, it explores allowable increases for units invested in stock and money market funds, assessing their effect on the optimum solution. Desklib provides access to this and other solved assignments to aid students in their studies.

Running head: LINEAR PROGRAMMING
Linear Programming
Name of Student:
Name of University:
Author’s Note:

1LINEAR PROGRAMMING
Table of Contents
Answer 1..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................2
Part c............................................................................................................................................2
Part d............................................................................................................................................2
Answer 2..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................2
Part c............................................................................................................................................2
Part d............................................................................................................................................2
Answer 3..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................2
Part c............................................................................................................................................2
Part d............................................................................................................................................2

2LINEAR PROGRAMMING

3LINEAR PROGRAMMING
Answer 1
Part a
The optimal solution for the solution is 5* 523.364486 + 8*1532.71028.
The value of the total annual return is 14878.50467.
Variable Cells
Final Reduced Objective Allowable Allowable
Cell Name Value Cost Coefficient Increase Decrease
$D$3 Shares of Petroluem Inc. 523.364486 0 5 12.33333333 0.636363636
$D$4 Shares of Quality Steel 1532.71028 0 8 1.166666667 5.692307692
Part b
The constraints Funds available and Risk Maximum are binding.
The objective’s for Funds available 30 P+55 Q≤ 100,000
and Risk maximum 0.65 P+0.30 Q ≤800 are the binding. Both the objectives are being used to
the maximum value’s.
Final Shadow
Cell Name Value Price
$F$5 100000 0.138317757
$H$5 800 1.308411215
$J$3 Shares of Petroluem Inc. 523.364486 0
Part c
The shadow price for “Funds available” is 0.1383. The shadow price for Risk maximum
is 1.3084. Hence unit increase in the prices of the constraints would increase the “Funds
available” by 0.1383 and “Risk Maximum” by 1.3084.

4LINEAR PROGRAMMING
Part d
The shadow price for Petroleum Inc. maximum is 0. Hence, any additional increase in the
amount invested in Petroleum Inc. maximum would result in no increase in total annual return.
Thus, investment in Petroleum Inc would not be beneficial.
Final Shadow
Cell Name Value Price
$F$5 100000 0.138317757
$H$5 800 1.308411215
$J$3 Shares of Petroluem Inc. 523.364486 0

5LINEAR PROGRAMMING
Answer 2
Part a
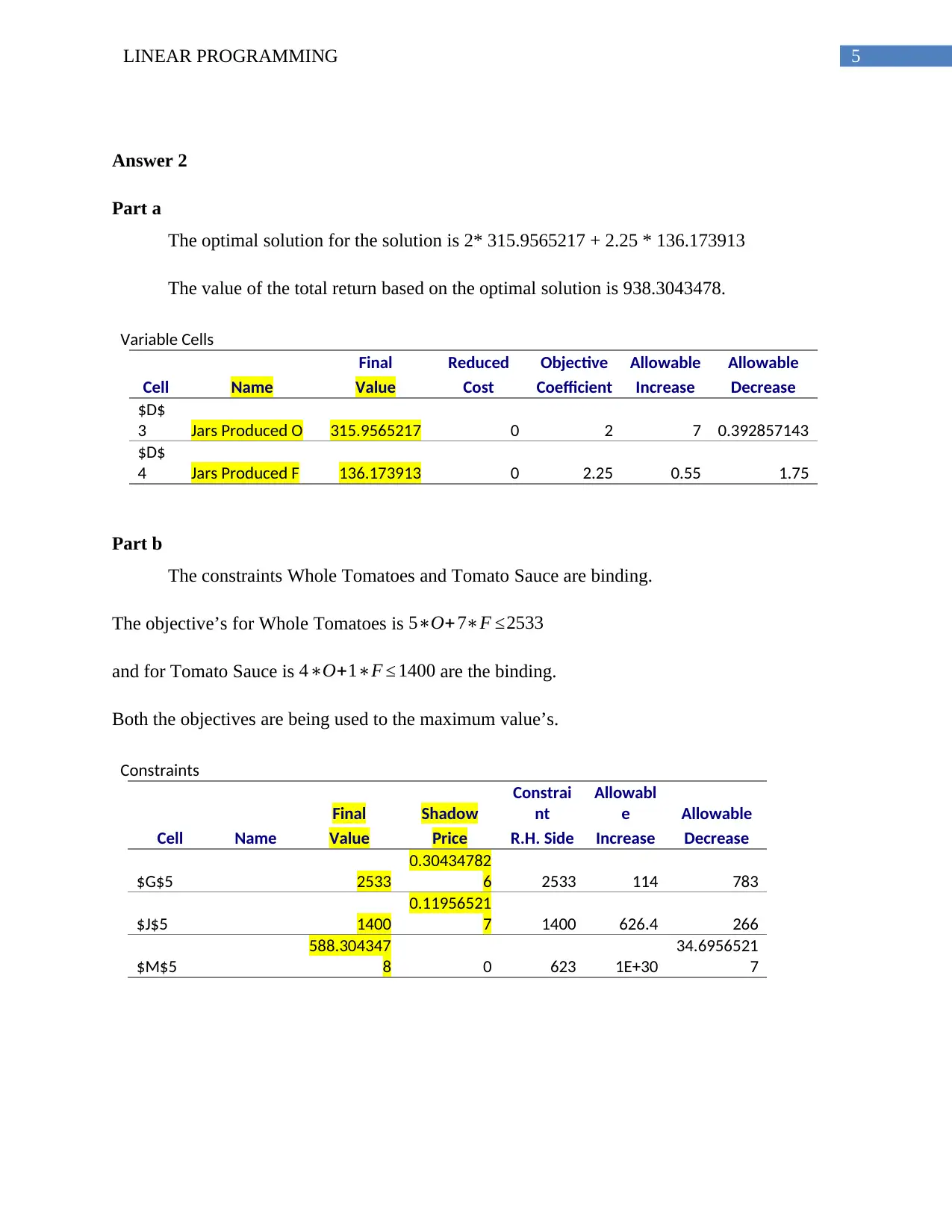
The optimal solution for the solution is 2* 315.9565217 + 2.25 * 136.173913
The value of the total return based on the optimal solution is 938.3043478.
Variable Cells
Final Reduced Objective Allowable Allowable
Cell Name Value Cost Coefficient Increase Decrease
$D$
3 Jars Produced O 315.9565217 0 2 7 0.392857143
$D$
4 Jars Produced F 136.173913 0 2.25 0.55 1.75
Part b
The constraints Whole Tomatoes and Tomato Sauce are binding.
The objective’s for Whole Tomatoes is 5∗O+ 7∗F ≤2533
and for Tomato Sauce is 4∗O+1∗F ≤ 1400 are the binding.
Both the objectives are being used to the maximum value’s.
Constraints
Final Shadow
Constrai
nt
Allowabl
e Allowable
Cell Name Value Price R.H. Side Increase Decrease
$G$5 2533
0.30434782
6 2533 114 783
$J$5 1400
0.11956521
7 1400 626.4 266
$M$5
588.304347
8 0 623 1E+30
34.6956521
7

6LINEAR PROGRAMMING
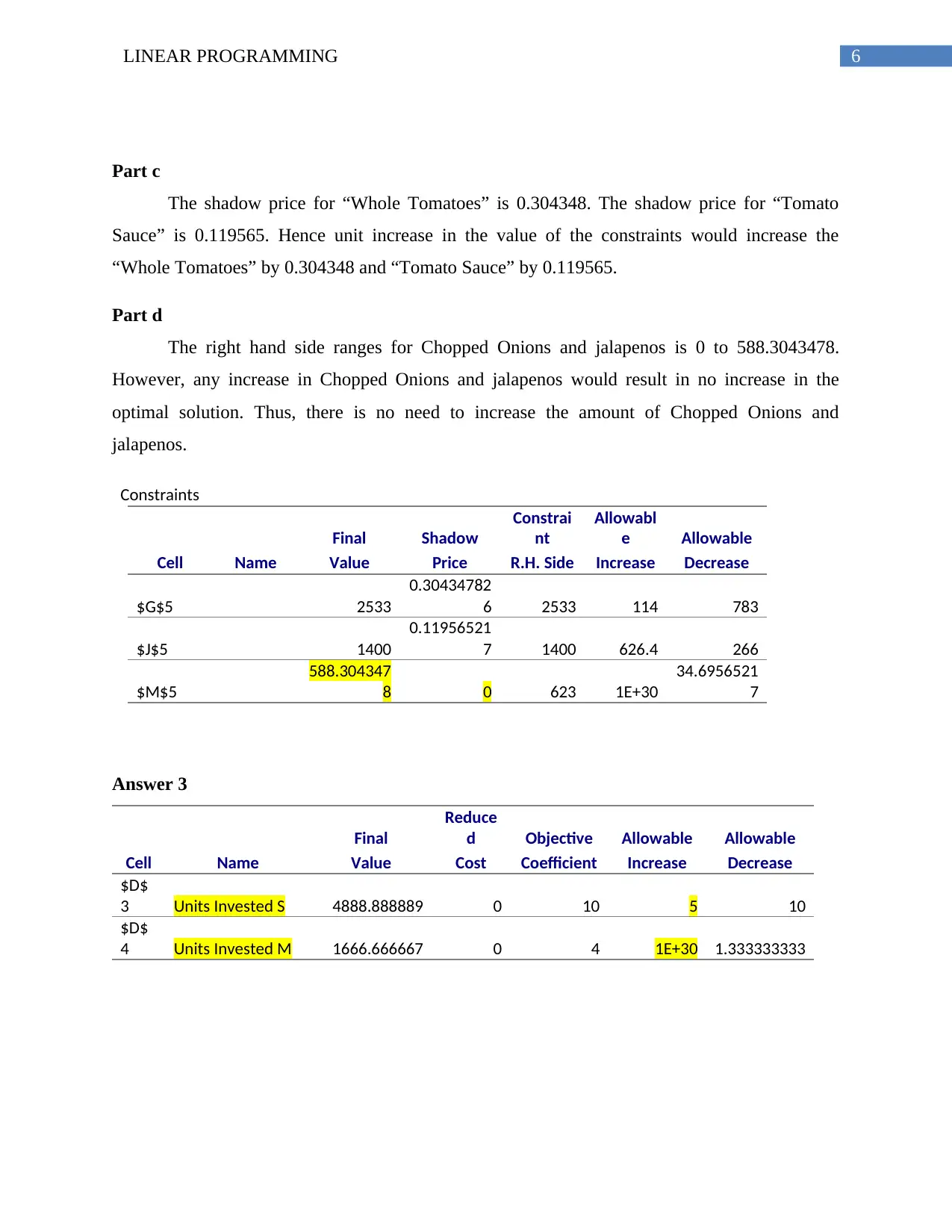
Part c
The shadow price for “Whole Tomatoes” is 0.304348. The shadow price for “Tomato
Sauce” is 0.119565. Hence unit increase in the value of the constraints would increase the
“Whole Tomatoes” by 0.304348 and “Tomato Sauce” by 0.119565.
Part d
The right hand side ranges for Chopped Onions and jalapenos is 0 to 588.3043478.
However, any increase in Chopped Onions and jalapenos would result in no increase in the
optimal solution. Thus, there is no need to increase the amount of Chopped Onions and
jalapenos.
Constraints
Final Shadow
Constrai
nt
Allowabl
e Allowable
Cell Name Value Price R.H. Side Increase Decrease
$G$5 2533
0.30434782
6 2533 114 783
$J$5 1400
0.11956521
7 1400 626.4 266
$M$5
588.304347
8 0 623 1E+30
34.6956521
7
Answer 3
Final
Reduce
d Objective Allowable Allowable
Cell Name Value Cost Coefficient Increase Decrease
$D$
3 Units Invested S 4888.888889 0 10 5 10
$D$
4 Units Invested M 1666.666667 0 4 1E+30 1.333333333

7LINEAR PROGRAMMING
Part a
From the solution it is seen that the Allowable increase for Units invested S is 5. Thus an
increase in the Units Invested in S by units would not change the optimum solution for its
present value of S = 4888.88 and M = 1666.666.
Part b
From the solution it is seen that the Allowable increase for Units invested M is 1E+30.
Thus an increase in the Units Invested in M by units would not change the optimum solution for
its present value of S = 4888.88 and M = 1666.666.
Part c
The allowable increase for “units purchased in stock fund” is 5 and for “units purchased
in money market fund” is 1E+30. Thus increasing “units purchased in stock fund” from 10 to 12
and “units purchased in money market fund” from 4 to 6 would not change the optimum number
of units purchased. Although, the total number of units purchased would increase.