Economics Report: Linear Regression Analysis of Graduation Rates

This report investigates the relationship between graduation rates (GR) and retention rates (RR) in higher education using simple linear regression analysis. The data, sourced from an online education database, includes GR and RR data from 29 different institutions. The analysis involves computing descriptive statistics, constructing a scatter diagram, and performing regression analysis using Microsoft Excel. The results indicate a weak positive linear association between RR and GR, with a correlation coefficient of 0.67. The estimated regression equation is Y = 0.285X + 25.423, where Y represents the graduation rate and X represents the retention rate. The slope coefficient suggests that for every 1% increase in retention rate, the graduation rate increases by 0.285%. The report also discusses the statistical significance and goodness of fit of the regression model, highlighting concerns for South University and the University of Phoenix based on their respective RR and GR. The report recommends that institutions adopt multiple regression models to incorporate more factors influencing graduation rates and introduce programs to improve student retention.

Economics And Quantitative Analysis
Linear Regression Report
Student’s Name
Institution Affiliation

1. Introduction
Purpose
The purpose of the report is to examine the level of association between two factors: Graduation
Rate (GR) and Retention Rate (RR). This will conducted by doing simple regression analysis
of the data of the two variables.
Background
Most students who enroll in the institutions of higher learning are failing to graduate today. It’s
has be reported that at least 305 of students who join universities and colleges drop out of
school after their first year of studies (Tinto, 2005) This has greatly affected family and
government as most students abandon studies when they have already family income,
government resources and acquired loan from government agencies. These pose big economic
issues in the country. As a result this has become a major concern for economists. The
investigation of the reason for low graduation rate among the students will play a great role. The
question how retention of student after enrollment influence graduation of students will be
examined to reveal the mystery of failure of student to make to graduation square after a
given tenor of studies.
Method
The data and methods that were employed are indicated below. The data comprise of GR and RR
of 29 different institutions of higher learning. The data was obtained from online Education

database. The methods that were used to investigate the relationship between GR and RR
include:
 Computation of the mean, standard deviation, minimum and maximum.
 Construction of the scatter diagram
 Doing simple regression analysis
These computation and analysis were done using Microsoft Excel software.
2. Results
a. Mean, Standard deviation, Minimum and Maximum
Below is a table that shows the results of the computation form excel
Statistics RR(%) GR(%)
Mean 57.41379 41.75862
Standard Deviation 23.24023 9.865724
Minimum 4 25
Maximum 100 61
Count 29 29
Results from the table above reveal that, the minimum value of Retention rate is less than that of
Graduation rate. However, RR has higher maximum value, mean and standard deviation than
GR.
b. Scatter Diagram

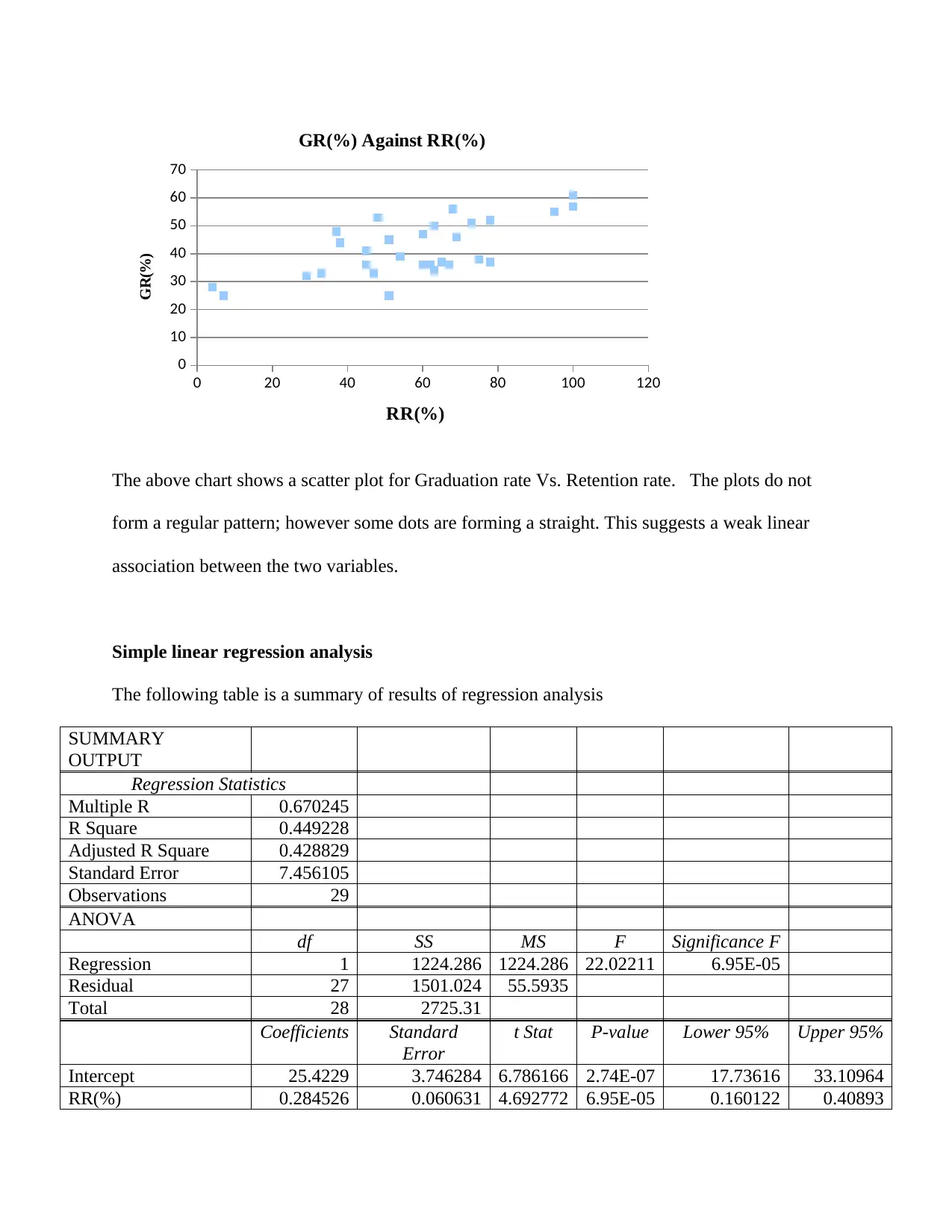
0 20 40 60 80 100 120
0
10
20
30
40
50
60
70
GR(%) Against RR(%)
RR(%)
GR(%)
The above chart shows a scatter plot for Graduation rate Vs. Retention rate. The plots do not
form a regular pattern; however some dots are forming a straight. This suggests a weak linear
association between the two variables.
Simple linear regression analysis
The following table is a summary of results of regression analysis
SUMMARY
OUTPUT
Regression Statistics
Multiple R 0.670245
R Square 0.449228
Adjusted R Square 0.428829
Standard Error 7.456105
Observations 29
ANOVA
df SS MS F Significance F
Regression 1 1224.286 1224.286 22.02211 6.95E-05
Residual 27 1501.024 55.5935
Total 28 2725.31
Coefficients Standard
Error
t Stat P-value Lower 95% Upper 95%
Intercept 25.4229 3.746284 6.786166 2.74E-07 17.73616 33.10964
RR(%) 0.284526 0.060631 4.692772 6.95E-05 0.160122 0.40893

From the results, the following has been obtained:
Correlation coefficient ( R ) between the RR and GR =0.670
Intercept coefficient between RR and GR =25.423
Slope coefficient = 0.285
The p-values (for RR and Intercept) of the significance of the model ≈ 0.000
d. Stating the estimated regression equation and interpretation of slope coefficient
The estimated equation will be written from Slope and intercept coefficient
Y =0.285 X +25.423 , w h ereY =GraduationRateandX =RententionRate
Interpretation:
The slope coefficient, 0.2845 implies that when retention rate increase by one 1% the
graduation rate will increase by 0.285% and vice versa.
e. Statistical Significance of the Simple Regression Equation
This is determined from the p-value of the intercept and slope coefficient. Seber& Lee (2012)
argue that the regression model will be statistically significant if the two p-values especially the
slope coefficient is less than 0.05. The p-values of RR is approximated to 0.000 which is less
than 0.05, and therefore, the simple regression model is statistically significant for the
association between Graduation rate and Retention rate.

f. Goodness fit of the simple linear regression model
This will be identified using the residual plot of the above simple regression model. Below is a
chart showing the residual plot
0 20 40 60 80 100 120
-20
-10
0
10
20
RR(%) Residual Plot
RR(%)
Residuals
The model is fit for the data of RR and GR as data plots are not forming a regular pattern and
data points are at the below and above the x-axis(Pardoe, 2012).
g. South University
The concern of South University is the big disparity between RR and GR. Its graduation rate is
below the retention rate by 26%, which indicates that most students that enroll in the South
university drop out of school before they complete their studies. This a reason for low graduation
rate (25%) in the university compared to retention rate (51%). This is a great worry of the South
university they enroll more students but they are only able to take few to the graduation square.

h. University of Phoenix
The main concern of the University of Phoenix is very low retention rate (4%) and graduation
rate (28%). This university has a better graduation rate than retention rate. This indicates that the
university is not able to retain student till graduation. This university needs to come up with
means that can address the needs of the students so that they are able to cope up to the end.
A major issue faced by the University of Phoenix is that 96% of students who enroll with the
school do not make it to graduation.
3. Discussion
The results that are key to this study are: scatter diagram and regression analysis. The aim of
the scatter plot is to depict the relationship between Retention Rate and Graduation Rate. Most
data dots of the scatter plot are a not aligned linearly, however, few data points are forming a
linear pattern. Also the points have positives slope due their left-right upward trend. This is an
indicator of a weak positive linear association between RR and GR (McClave e tal, 2003).
From the regression analysis result, correlation coefficient (R is 0.67 which close to 1 than 0. states
that the value of R is an indicator of high positive correlation (Francis, 2008). Therefore, since
the correlation between graduation and retention rate is close to +1, their relationship will be said
to be a positive linear relationship.
The report explains the level of association between RR(%) and GR(%). This knowledge can
vital to the university management as it can be used to understand the impact of retention
rate on the number of student who are expected to be graduated from the university after a

given tenure of studies. This will help the management to plan ahead for their graduation. Also
management will be able to come up with better means of maintaining and retaining students in
school as way of ensuring high retention rate and graduation rate for the school. . On the other
hand the limitation of study is that the simple linear regression model only considers a single
factor(RR) and does not factors in other inputs that can affect retention and graduation rate,
therefore this model will not ideal for some institutions. The findings are consistent with others
studies. Other studies indicate that at least 30% of students do not graduates, this concur with
statistical mean of graduation rate, which 41.8%. Graduation rate of 41.8% indicates more than
52% of the students who enroll to the university do not graduate.
4. Recommendations
The following are recommendation from the results and discussion.
First, the report can be adopted and implemented by institutions’ managements; they can adopt
the regression model in understanding the effects of retention rate on Graduation rate.
A suitable model, like multiple regression models should be adopted in place of simple linear
regression model to incorporate more factors that influence graduation rate of different schools.
Finally, institution school should introduce programs in the school that can help student from
abandoning their studies. Improving their retention rate and hence graduation rate should be their
focus.

Reference
Francis, A., 2008. Business Mathematics and Statistics. South Western Cengage Learning
EMEA, High Holborn House. 50-51 Bedford Row, London WC1R 4LR. ISBN 978-1-84480-128-
2.
McClave, J.T., Sincich, T. and Sincich, T.T., 2003. A first course in statistics. Pearson
Education.
Pardoe, I., 2012. Applied regression modeling: A business approach. John Wiley & Sons.
.
Tinto, V., 2005. College student retention: Formula for student success. Greenwood Publishing
Group.
Seber, G.A. and Lee, A.J., 2012. Linear regression analysis(Vol. 329). John Wiley & Sons.