M269 Algorithms, Data Structures and Computability TMA Fall 2018/2019

This document presents solutions to several questions related to algorithms, data structures, and computability. It covers matrix multiplication algorithm analysis, including its time complexity of O(n^3). The document also explains Euler paths and circuits, providing examples and modifications to create an Euler circuit from a given graph. Further, it includes solutions for summation problems, optimizing floating-point arithmetic operations. Lastly, it provides an algorithm and analysis for a function that counts inversions in an array, determining its time complexity to be O(n^2).

Contents
Question 1.............................................................................................................................................1
Question 1.a......................................................................................................................................1
Question 1.b.....................................................................................................................................1
Question 2.............................................................................................................................................1
Question 2.a......................................................................................................................................1
Question 2.b.....................................................................................................................................2
Question 2.C.....................................................................................................................................3
Question 3.............................................................................................................................................3
Question 3.a......................................................................................................................................3
Question 3.b.....................................................................................................................................4
Question 4.............................................................................................................................................4
Question 4.a......................................................................................................................................4
Question 4.b.....................................................................................................................................5

Question 1
Question 1.a
Algorithm MatrixMult (A[n][n], B[n][n], C[n][n])
for i = 0 to n-1
for j = 0 to n-1
sum = 0
for k = 0 to n-1 sum = sum + A[i][k] * B[k][j]
C[i][j] = sum
Question 1.b
T (n)=∑
i=0
n−1
❑∑
j=0
n−1
∑
k=0
n−1
2=2 n3 = O(n3))
Question 2
Question 2.a
Euler path
Euler path is a path and that uses every edge of a graph exactly once that is called as
Euler Path. In this path start and ends with different vertices.
Euler Circuit
The Euler circuit based on the Euler path. The Euler circuit is a circuit and that uses
every edge of a graph exactly once that is called as the Euler circuit. This circuit start and
ends with the same vertex.

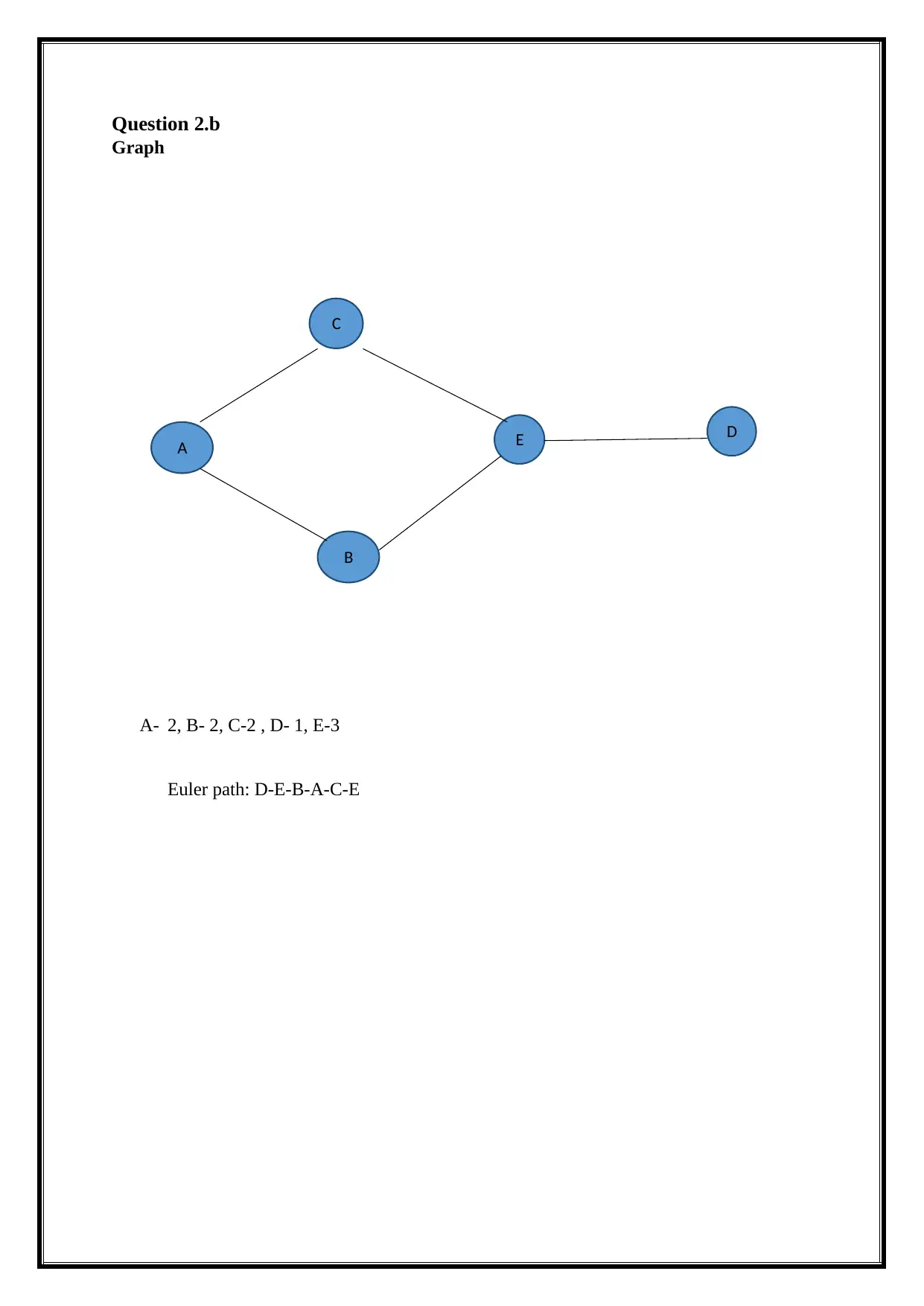
Question 2.b
Graph
A- 2, B- 2, C-2 , D- 1, E-3
Euler path: D-E-B-A-C-E
A
C
B
E D

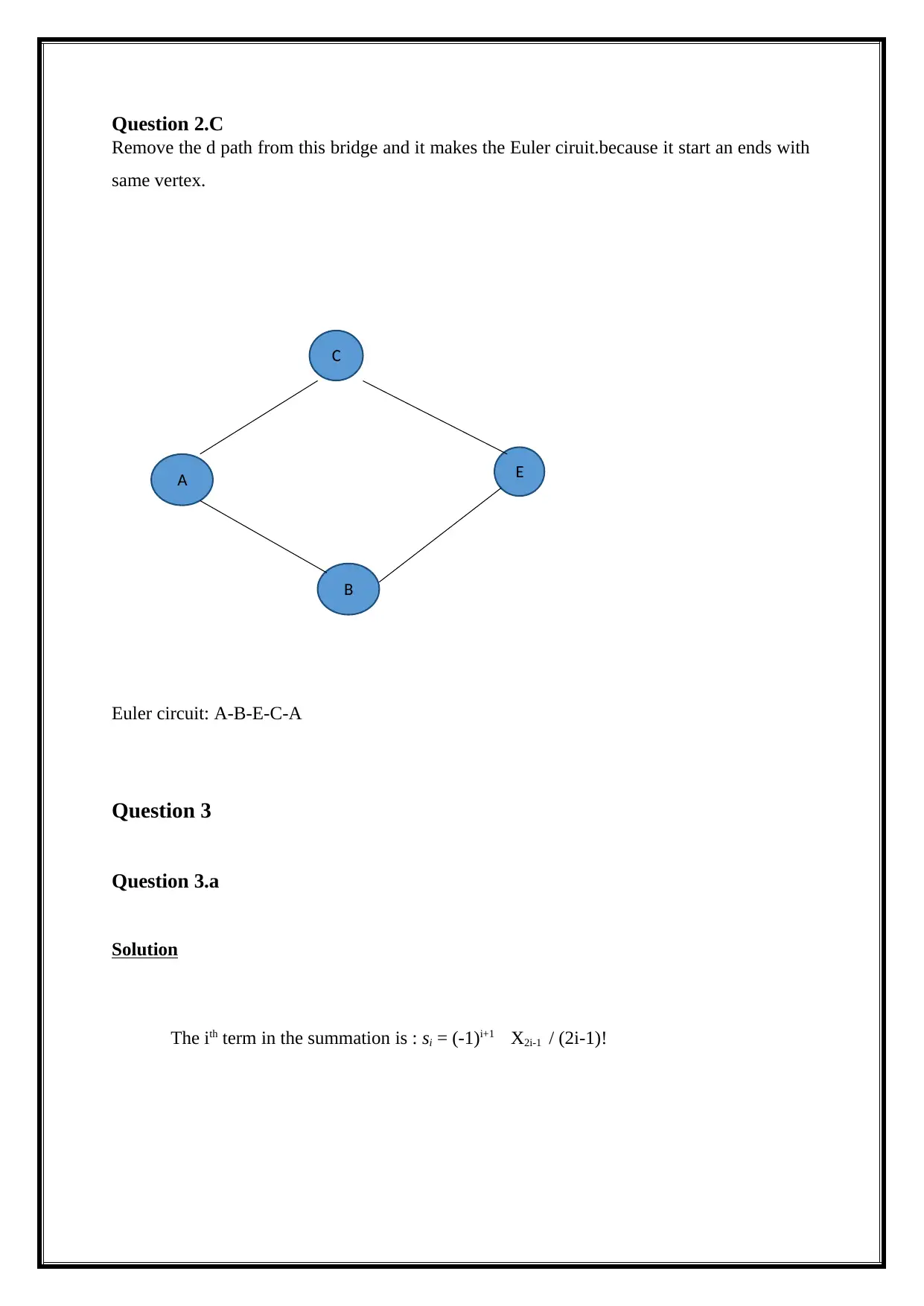
Question 2.C
Remove the d path from this bridge and it makes the Euler ciruit.because it start an ends with
same vertex.
Euler circuit: A-B-E-C-A
Question 3
Question 3.a
Solution
The ith term in the summation is : si = (-1)i+1 X2i-1 / (2i-1)!
A
C
B
E

(−x2 )
Then si = (2i − 2)(2i −1) si−1 for i >1with s1 =x
s = x; sum = s; y = -x*x; // 2 float arithmetic operations for i = 2 to n
m = 2*i; a = (m -2)*(m-1); // These do not contain float arithmetic
s = y/a * s; sum = sum + s; //3 float arithmetic operations
Question 3.b
The ith term in the summation is : si = (-1)i+1 X2i-1 / (2i-1)!
Then si =(-x2)/(2i − 2)(2i −1) si−1 for i >1with s1 = x
s = x;
sum = s;
y = -x*x for i = 2 to n
s = y/a * s;
sum = sum + s;
Hence T(n) = 3(n-1) + 2 float arithmetic operations.
Question 4
Question 4.a
Algorithm
int F(A,n)
S = 0;
for i = 0 to n-2
for j = i+1 to n-1

if (Ai > Aj) S++
return S
Question 4.b
Analysis
n−2 n−1 n−2 n−1
T( n ) = ∑ ∑1 = ∑( n − i − 1 ) = ∑i = n( n − 1 ) / 2 = O( n 2 )
i =0 j=i+1 i=0 i=1