Machine Learning for Student Success: ABCEU Project Report Analysis

This report presents an analysis of student data from ABC Universal Education (ABCEU) to predict pass rates using machine learning techniques. The objective is to identify factors that significantly influence student success. The analysis employs a data-driven approach, utilizing machine learning algorithms including Decision Trees, Random Forest, and Generalized Linear Models (GLM). After data exploration and feature selection, the models are implemented in R, and their performance is evaluated using metrics such as accuracy, sensitivity, specificity, and the confusion matrix. The Random Forest model demonstrates the highest accuracy. The report includes an executive summary, data exploration, feature selection, model selection, and validation. The findings provide insights into the most relevant factors determining student pass rates, offering ABCEU actionable recommendations to improve student outcomes.

1
Executive Summary
Objective
To examine the factors that can be used to determine the pass rate for students in the GP (Grand
Pines) or MHS (Marble Hill School)) schools to aid in the process of decision making process in
the ABC Universal Education (ABCEU).
Approach
Using a data analysis approach which incorporates the use of machine learning algorithms which
include: Decision Trees, Random Forest, Generalized Linear Models in which case this paper
uses a logistic regression of the binomial family. After conducting feature selection, the models
are implemented in R and the performance of the models assessed through the comparison of
their respective accuracy performance and predictive power which is presented in the confusion
matrix obtained for each model.
Results
After implementing the GLM model twice, the second model returned an accuracy score of
77.75% while the Decision Tree model recorded an accuracy of 96.16 and the random forest had
an accuracy of 99.47%. In this regard, we chose the Random forest as the most relevant
algorithm and used the variable importance plot to analyze the most probable factors that can be
used to determine the pass rate of students.
Conclusion
Different machine learning algorithms perform differently under different situations and
depending on the original requirement of the exercise. Therefore, the use of an algorithm should
be based on the requirement. In order to access the optimal model performance metrics should be
defined i.e. confusion matrix in this paper.

2
Data Exploration and Feature Selection
Data Exploration
In machine learning, the very basic objective is to try and gain an understanding of the data that
is presented to the analyst. In this respect, the question of what really is in the data crops up
crops up. Most often, machine leaning algorithms have been proven effective in offering a means
as to which the analyst can use to answer such a question (Sutton, 2018). Some of the popular
data exploration methods include visual data exploration and descriptive data analytics both of
which are used to gain understanding of factors such as the distribution of data attributes,
outliers, normality of the data and determine which factors are correlated, etcetera. In this paper
we will only explore univariate distributions of the data to examine: measures of location and
spread, asymmetry, outliers, missing data and gaps.
Descriptive
Table 1: List of data attributes
As evidenced from table 1, there are 33 variables but only 29 are predictor and 1 is the target
variable (G3). In addition, there were no missing observations in the data so we did not conduct
any imputing:

3
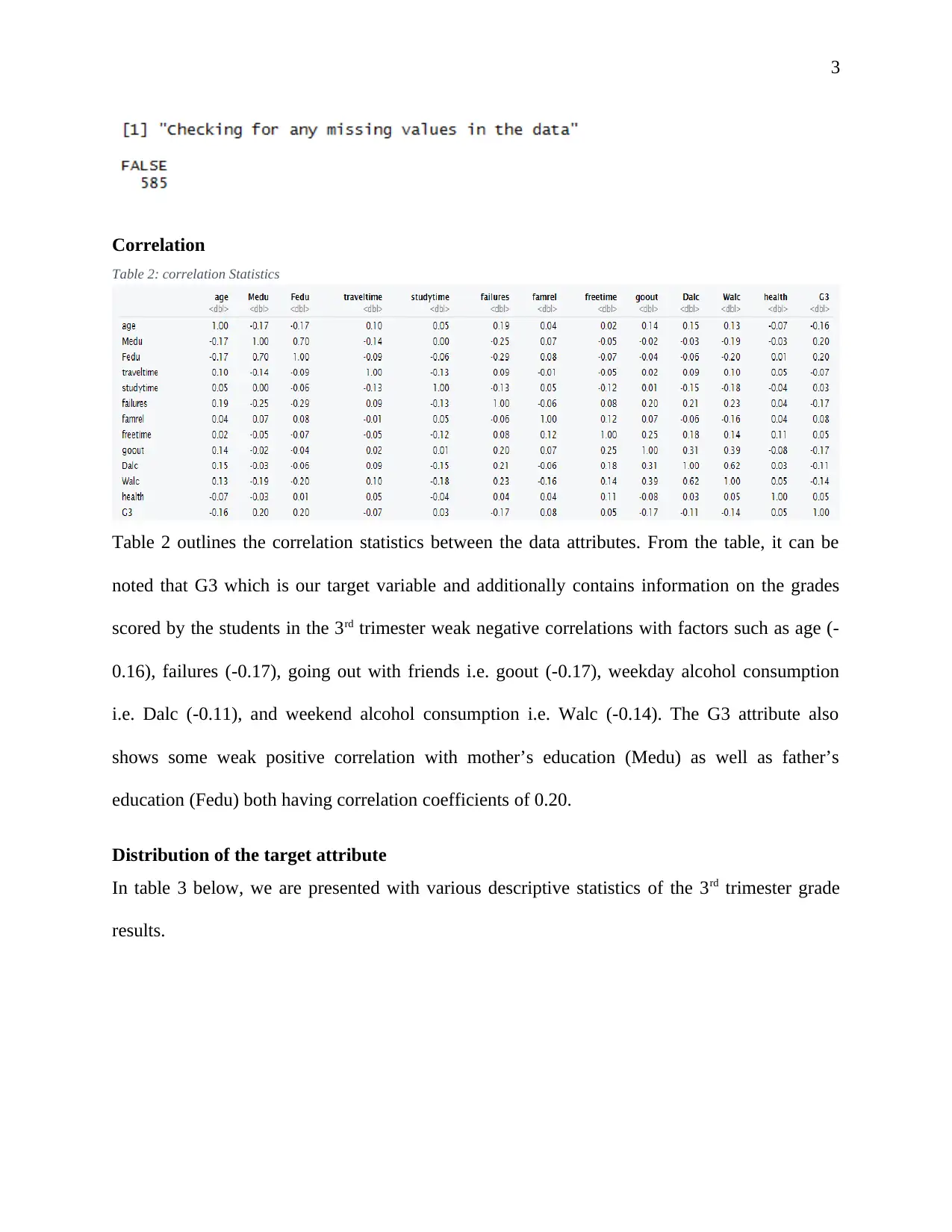
Correlation
Table 2: correlation Statistics
Table 2 outlines the correlation statistics between the data attributes. From the table, it can be
noted that G3 which is our target variable and additionally contains information on the grades
scored by the students in the 3rd trimester weak negative correlations with factors such as age (-
0.16), failures (-0.17), going out with friends i.e. goout (-0.17), weekday alcohol consumption
i.e. Dalc (-0.11), and weekend alcohol consumption i.e. Walc (-0.14). The G3 attribute also
shows some weak positive correlation with mother’s education (Medu) as well as father’s
education (Fedu) both having correlation coefficients of 0.20.
Distribution of the target attribute
In table 3 below, we are presented with various descriptive statistics of the 3rd trimester grade
results.

4
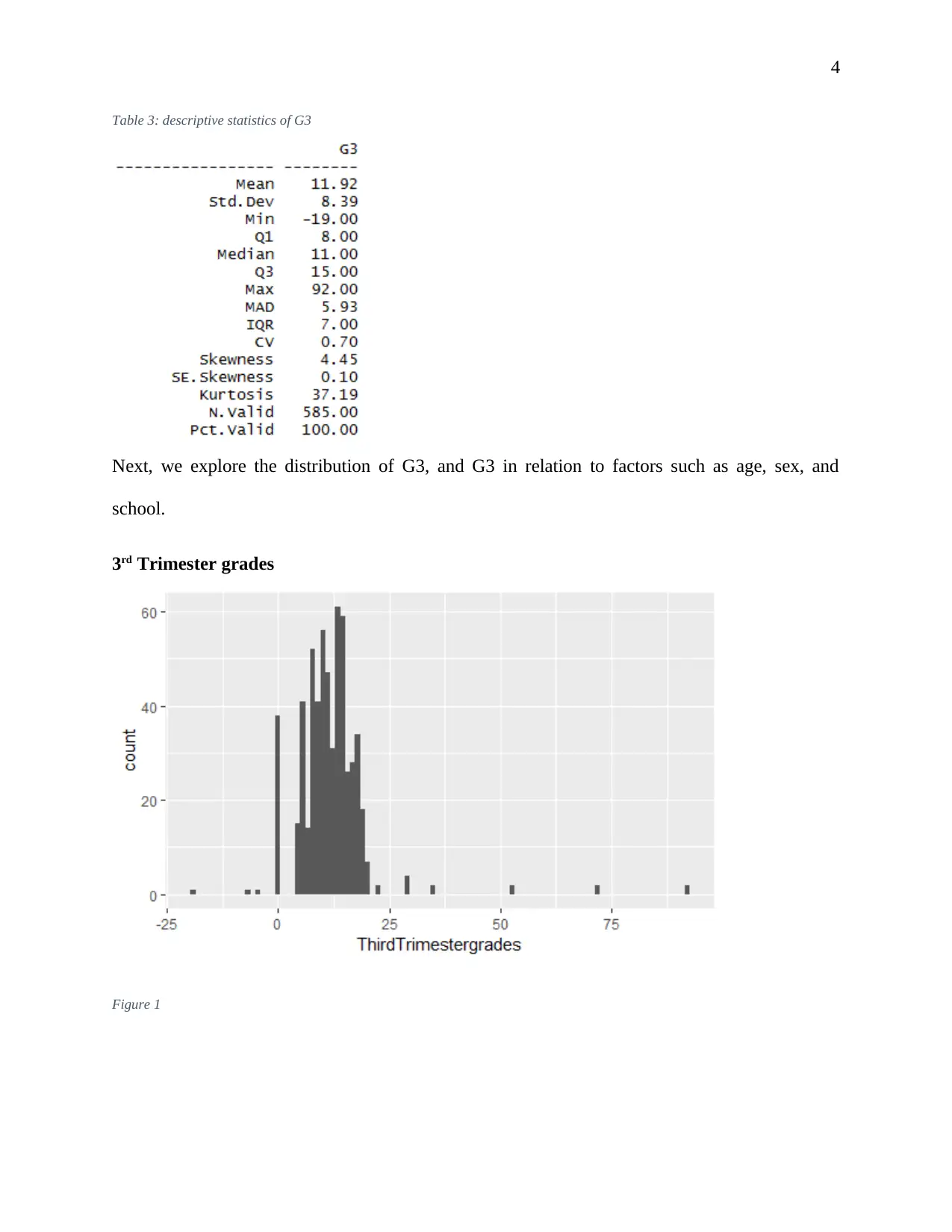
Table 3: descriptive statistics of G3
Next, we explore the distribution of G3, and G3 in relation to factors such as age, sex, and
school.
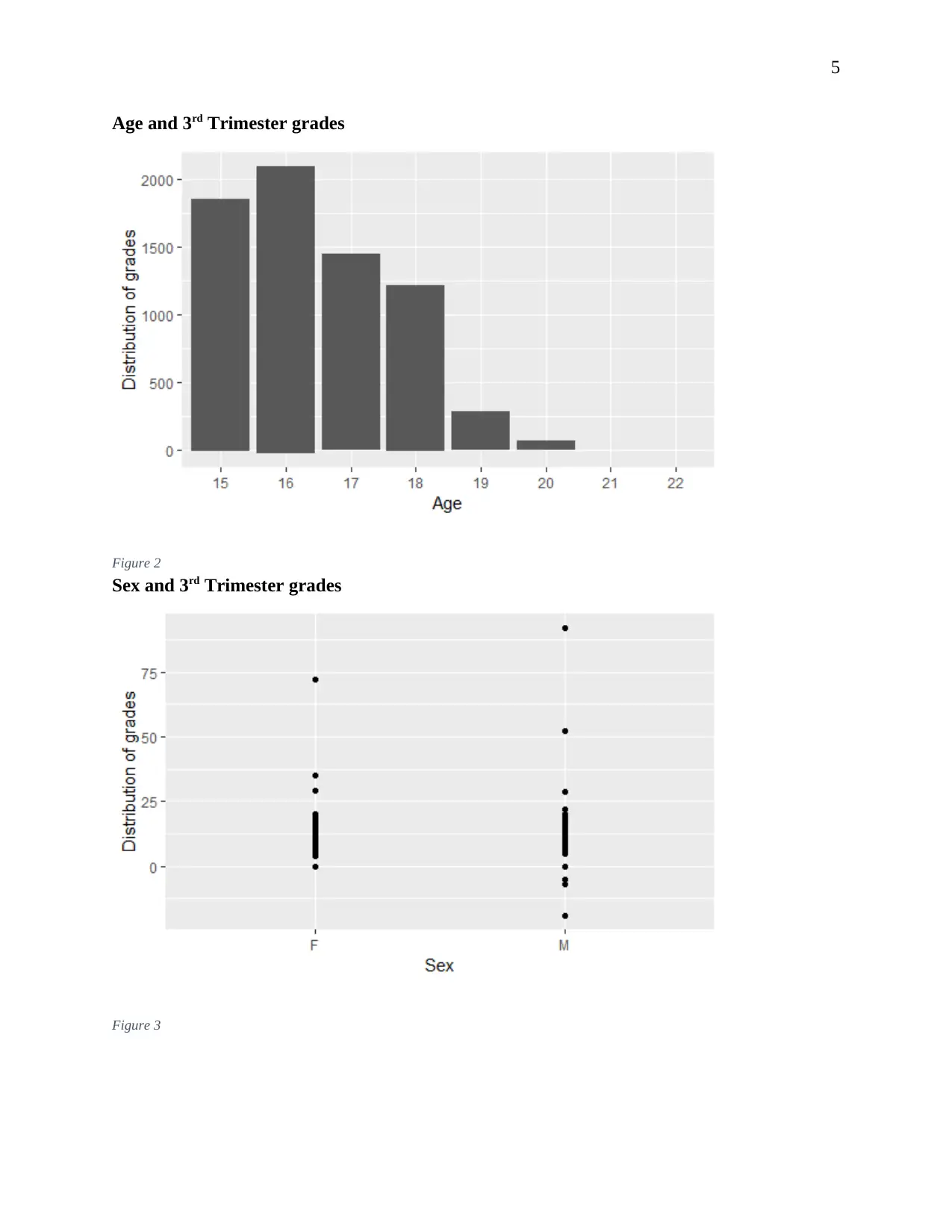
3rd Trimester grades
Figure 1

5
Age and 3rd Trimester grades
Figure 2
Sex and 3rd Trimester grades
Figure 3

6
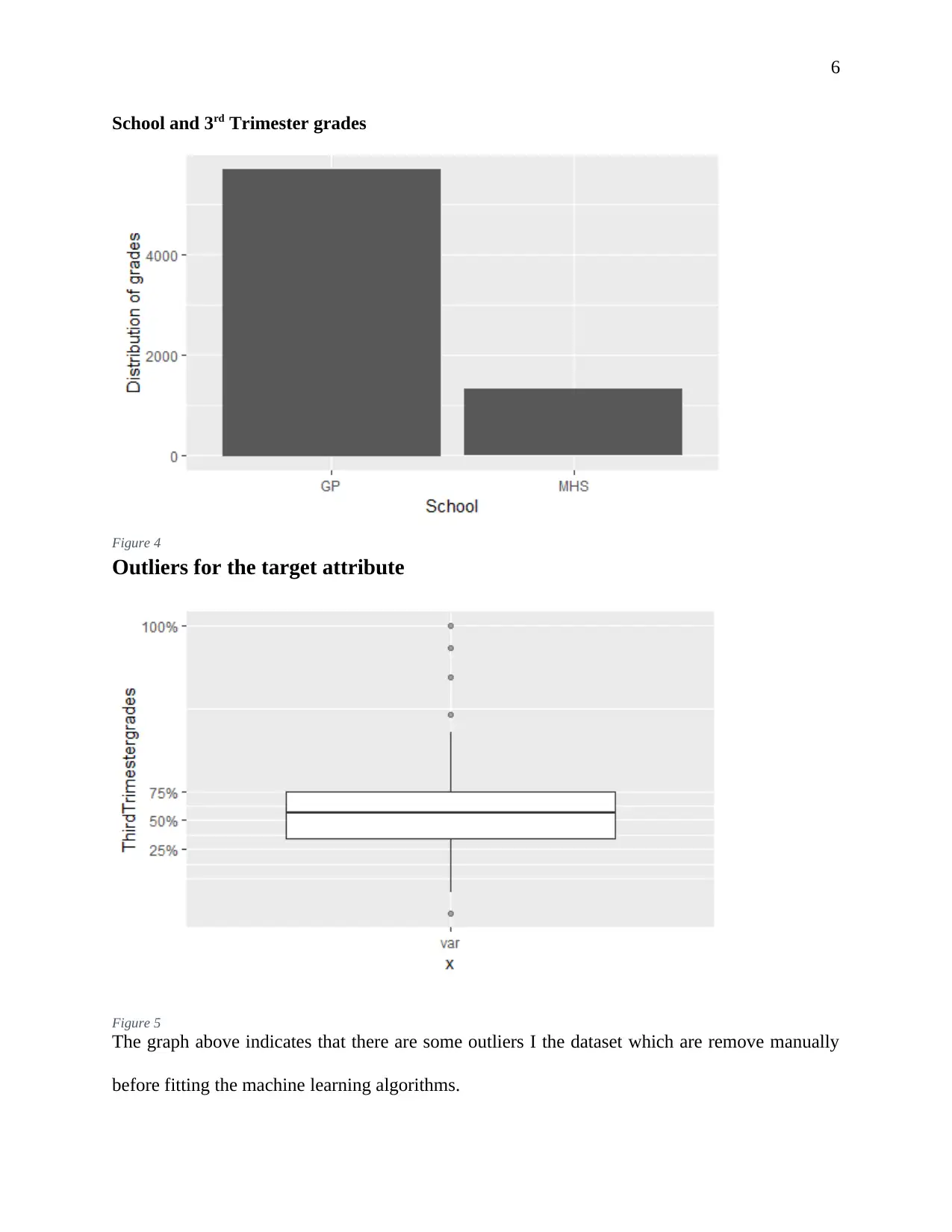
School and 3rd Trimester grades
Figure 4
Outliers for the target attribute
Figure 5
The graph above indicates that there are some outliers I the dataset which are remove manually
before fitting the machine learning algorithms.

7
Feature Selection
Performance of machine learning algorithms work in a way such that they are dependent of the
kind of data used when implementing them. Feature selection is the process through which the
dimension of data used in predictive analysis is reduced (Choudhury, 2019). Feature selection
can include algorithms such as wrapper methods which is used in this study where we use the
genetic algorithm which is used to find a subset of features from the dataset. The wrapper
algorithm is efficient due to its ability to maintain the characteristics of the featured variables and
ability to render effective search in return.
For instance, using the wrapper algorithm the following were done:
i. A new measure of performance was created to define a criterion to determine when a
student has passed or failed
ii. Dropped irrelevant entries such as the observations when the score of education for the
either the mother or father were 0.
iii. Dropped the scores for both the 1st and 2nd trimester and the absence variable
Model Selection and Validation
The objective of this paper is to determine which factors can be used to determine the pass rate
for students.
In order to address the study’s objective, our analysis will involve the application of three
machine learning models i.e. two classification models and one prediction model to the data.
Specifically, the classification algorithms are decision trees and Random Forest while the
predictive model is a Generalized Linear Model.

8
Performance metrics for model selection
Machine learning models often show a difference in performance under different circumstances.
Different studies have attributed such differences to a number of factors including the kind of
data used, the machine learning problem etcetera. The problem in machine learning therefore lies
in determining which model is the best for the problem at hand (Brownlee, 2016). To address
this problem, it is crucial to run different models on the same training, test, and validation
datasets. After running sufficient number of models the next task is to set metrics with which to
gauge the models performance against whereby in this study we chose to use the confusion
matrix as a performance measurement metric (Pavlyshenko, 2019).
Confusion matrix
According to Brownlee (2019), “… a confusion matrix, also known as an error matrix, is a
specific table layout that allows visualization of the performance of an algorithm.” As such, the
confusion matrix offers performance measures of the models including their classification
accuracy which can be misleading at times hence it is better to include other measures such as
sensitivity, specificity, precision, and balanced accuracy. A model with good performance often
shows higher scores in these statistics.
Basic evaluation measures
These are the measures that we will use to compare the performance of the models used in this
studies. They include:
Accuracy
It shows the total number of accurate predictions / classifications made by the model where the
best accuracy is 1.0 and the worst is 0.0.

9
Prevalence and Precision
Prevalence is a measure of how often the positives (yes) occurs in the sample while precision is a
measure of how accurate the model predicts yeas in the sample
Sensitivity and specificity
While sensitivity measures the proportion of actual positives that are identified by the model,
specificity measures the true negatives that have been correctly identified by the model.
Generalized Linear Model (GLMs)
Unlike a linear model which assume that the outcome of input features into the model will have a
Gaussian distribution, GLMs assume that the outcomes are Non-Gaussian. In the linear models,
the prediction of categorical outcomes are restricted in which case a GLM is adopted as an
extension (Molnar, 2019). The basic idea for GLM build up is: “Keep the weighted sum of the
features, but allow non-Gaussian outcome distributions and connect the expected mean of this
distribution and the weighted sum through a possibly nonlinear function” (Molnar, 2019). GLM
models generally take the form:
Where; g is a link function, Ey is the probability distribution of the exponential family, and XTβ
is the linear predictor. To examine the performance of the GLM we will explore the models fit
and the prediction accuracy as well as related metrics.
The main advantage of the Generalized Linear model is its ability to be extended incorporating
many variables. However, this acts as its demerit since the sophistication of GLMs often lead to

10
problems in interpretation and at times fail to work in situations where there are non-linear
features (Molnar, 2019).
Implementation results
The implementation has two applications i.e. with many variables and with a smaller set of
variables.
Model fit
Table 4: many variables

11
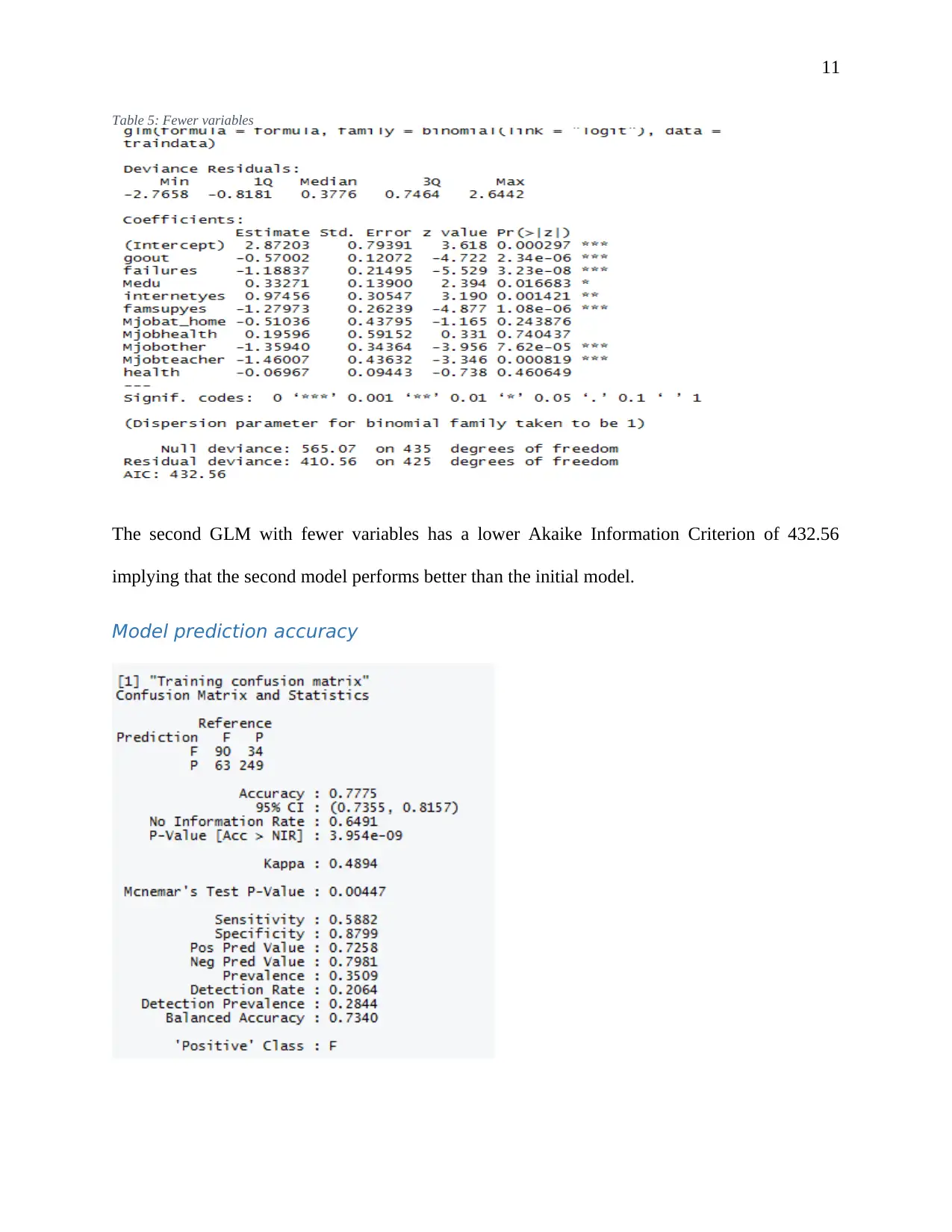
Table 5: Fewer variables
The second GLM with fewer variables has a lower Akaike Information Criterion of 432.56
implying that the second model performs better than the initial model.
Model prediction accuracy

12
After fitting our GLM, we note that the model has a classification accuracy on the training set of
77.75%, a balanced accuracy of 73.40%, a detection rate of 20.64% which is relatively low,
sensitivity of 58.82% and a specificity rate of 87.99%. The model however under performs when
fitting it with test data where the performance metrics are: a classification accuracy on the test set
of 68.75%, a balanced accuracy of 61.55%, a detection rate of 13.19%, sensitivity of 38.00 %
and a specificity rate of 85.11%. In addition, the Mcnemar’s Test P-value is 0.01707 which is
less than 0.05 at 95% confidence level indicating the model is sufficiently significant for
classification
Decision Trees
Decision trees in machine learning are often used visually and explicitly in the representation of
outcome decisions. In decision trees, the outcome is displayed in a downward where, the base
represents the condition whose basis is on the branches and the non-split nodes are the decisions.

13
Decision trees are categorized under tree-ensemble models and are great in indicating the path to
different possibilities which lead to a desirable outcome i.e. they can show dead ends and better
paths to meaningful decisions. However, on the downside decision trees are devoid of innovation
where, “…only past experience and corporate habit go into the “branching” of choices; new
ideas don’t get much consideration” (Sutton, 2018)
Implementation
Model fit
Figure 6: Decision tree
In figure six, the condition for passing or failing is that the 3rd trimester results be such that, if
less than 9.5 then the student has failed otherwise if greater than 9.5 the student has passed.
Model accuracy
We examine the confusion matrix of the model after application to both the test and train data;

14
Table 6
The model however under performs when fitting it with test data where the performance metrics
are: a classification accuracy on the test set of 100%, a balanced accuracy of 100%, a detection
rate of 35.09%, sensitivity of 100 %, a specificity rate of 100%, a no information rate of 64.91%
and a p-value [Acc > NIR] which is approximately less than 0.000 at 95% confidence interval. In
addition, the Mcnemar’s Test P-value is approximately 0.000 given a Kappa of 1 which is less
than 0.05 at 95% confidence level indicating the model is sufficiently significant for
classification.
Random Forest
According to an article published in “Towards data Science”, a Random Forest model is a
flexible learning model which outputs, with or without a hyper-parameter tuning, and has good
performance mostly compared to most algorithms. The model has a wide application due to its
use in both classification and prediction abilities (Donges, 2018).

15
The main advantages of random forest are that it is among the most accurate machine learning
algorithms at the moment. In addition, the bootstrapping of the model helps reduce bias and
making the model robust as well as more accurate. It also solves the problem of overfitting that
can be present in regression models. Moreover, a random forest model can be used in both
prediction and classification problems. However, “…The main drawback of Random Forests is
the model size. You could easily end up with a forest that takes hundreds of megabytes of
memory and is slow to evaluate”(Deeb, 2015).
Implementation
Model accuracy

16
The model however under performs when fitting it with test data where the performance metrics
are: a classification accuracy on the test set of 100%, a balanced accuracy of 100%, a detection
rate of 34.72%, sensitivity of 100 %, a specificity rate of 100%, a no information rate of 65.28%
and a p-value [Acc > NIR] which is approximately less than 0.000 at 95% confidence interval. In
addition, the Mcnemar’s Test P-value is approximately 0.000 given a Kappa of 1 which is less
than 0.05 at 95% confidence level indicating the model is sufficiently significant for
classification.
Comparing the results.
Performance of machine learning algorithms is accessed through the use of a confusion matrix
also known as an error matrix. It is useful in the measurement of Recall, Precision, Specificity,
Accuracy as well as the AUC-ROC Curve. Now let’s consider the performance metrics a
presented by the confusion matrix for each of the models. Evidently, from the tables, the random
forest model has the highest prediction accuracy of 99.47% while the decision model has the
second highest accuracy of 96.16% and the GLM has the least prediction accuracy of 77.75%.

17
These statistics are in tandem with the sensitivity, prevalence, and detection rates where the
random forest has the highest performance where the GLM has a sensitivity and specificity score
of 58.82% and 87.99% respectively while the Decision Tree has a specificity and sensitivity of
100% each similar to the scores by the Random forest nut a lower no information rate of 64.91%
compared to that of the Random Forest of 6528%. As such, the random forest would be the best
model fo0r use in our classification.
Findings and Recommendations
To reiterate, the aim of this study is to determine which factors can be used to determine the pass
rate.
Findings
From the preceding section, we noted that the Random forest would be the ideal model to use
due to its high prediction accuracy. In figure 7 the random forest model outputs a list of the most
important variables that predicts if a student passes or fails. We examine the 6 most important
variables as shown by the variable importance plot from the random forest model, generally this
plot indicates how important the variables are to predict the target attribute. The variables are:
the grades scored in the 3rd trimester, combined education (father’s education * mother’s
education), internet access, failures, Fedu (fathers education), and Dalc (Alcohol consumption
during weekday), and family relationships.
Recommendation
Analysis as presented in the previous sections has proven that various factors influence the
passing or failing of a student. As such, to improve performance, the factors that affect student
performance negatively should be addressed through institution of counter measures towards the

18
attributes and the measures that promote better performance reinforced. In this section we
provide implementable solutions to the problem posited to exist by the management. The
recommendations are:
Conduct drug awareness campaigns so as to sensitize the students on the effects of drugs such as
alcohol consumption towards their performance in academics. This can be through setting up
workshops, using media, etcetera. Theoretically, alcohol consumption has a negative effect on
concentration hence its use requires a counter-measure by the management.
Other factors such as family relations came up as an attribute which affects performance. It is
generally crucial that the firm develops and implements mechanisms which a noted earlier can be
counter-measures or pro-measures depending on the modelled relationships between the target
attribute and the predictor factors.
The role of data analytics in exploring underlying patterns has proven crucial. As such, the firm
should consider integration of data analytics tool as an aid to the process of decision–making in
the firm. This way, the management will be able to form and adopt well-informed decisions such
as which has been demonstrated in this paper.
References
Brownlee, J., 2016. How To Compare the Performance of Machine Learning Algorithms in
Weka. [Online]

19
Available at: https://machinelearningmastery.com/compare-performance-machine-learning-
algorithms-weka/
[Accessed 22 May 2019].
Choudhury, A., 2019. What Are Feature Selection Techniques In Machine Learning?. [Online]
Available at: https://www.analyticsindiamag.com/what-are-feature-selection-techniques-in-
machine-learning/
[Accessed 19 May 2019].
Deeb, A. E., 2015. The Unreasonable Effectiveness of Random Forests. [Online]
Available at: https://medium.com/rants-on-machine-learning/the-unreasonable-effectiveness-of-
random-forests-f33c3ce28883
[Accessed 20 May 2019].
Donges, N., 2018. The Random Forest Algorithm. [Online]
Available at: https://towardsdatascience.com/the-random-forest-algorithm-d457d499ffcd
[Accessed 19 May 2019].
Molnar, C., 2019. Interpretable machine learning. A Guide for Making Black Box Models
Explainable. 1st ed. Arizona: Bookdown.
Pavlyshenko, B. M., 2019. Machine-Learning Models for Sales Time. Lviv, Ukraine, SoftServe.
Sutton, C., 2018. Machine Learning for Data Exploration and Generation. Edinburgh, Jekyll.

20
Appendix
Rcodes
library(readxl)
BusinessAnalytic <- read_excel("BusinessAnalytic.xlsx",1)
library(summarytools)
"List of variables in the dataset"
array(names(BusinessAnalytic))
"There are 33 variables"
summarytools::descr(BusinessAnalytic$G3)
#Number of rows
nrow(BusinessAnalytic)
library(tidyverse)
library(caret)
library(GGally)
library(treemap)
G33=as.data.frame(BusinessAnalytic$G3)
colnames(G33)[colnames(G33)=="BusinessAnalytic$G3"] <- "ThirdTrimestergrades"
head(G33)
ggplot(G33, aes(ThirdTrimestergrades)) +
geom_histogram(bins = 100)
ggplot(BusinessAnalytic, aes(as.factor(BusinessAnalytic$sex), BusinessAnalytic$G3)) +
geom_point() +
labs(y = "Distribution of grades", x = "Sex");
ggplot(BusinessAnalytic, aes(as.factor(BusinessAnalytic$age), BusinessAnalytic$G3)) +
geom_bar(stat = "identity") +
labs(y = "Distribution of grades", x = "Age");
ggplot(BusinessAnalytic, aes(as.factor(BusinessAnalytic$school), BusinessAnalytic$G3)) +
geom_bar(stat = "identity") +
labs(y = "Distribution of grades", x = "School");
p1 <- ggplot(G33, aes("var", ThirdTrimestergrades)) +
geom_boxplot(outlier.alpha = .25) +
scale_y_log10(
breaks = quantile(G33$ThirdTrimestergrades) )
gridExtra::grid.arrange(p1)
#Quick look at G3
table(BusinessAnalytic$G3)
"Checking for any missing values in the data"
table(is.na(BusinessAnalytic$G3))
# Create a new variable that assigns pass "P" to those with G3 >= 10.
BusinessAnalytic$G3.Pass.Flag <- as.factor(ifelse(BusinessAnalytic$G3 >= 10, "P", "F"))
#Dropping G1, G2, and absences.
BusinessAnalytic<-BusinessAnalytic[-(30:32)]
##Remove the zero values for Medu and Fedu. I will retain the 10 cases where Dalc = 5.
## Variable exploration

21
# Remove records with questionable variable values.
# Remove the five records with parents education = 0.
BusinessAnalytic <-BusinessAnalytic[BusinessAnalytic$Medu > 0,]
BusinessAnalytic <- BusinessAnalytic[BusinessAnalytic$Fedu > 0,
# Check that records removed did not overlap
#Number of rows
nrow(BusinessAnalytic)
## Calculate correlations for numerical variables
numericvars <-names(BusinessAnalytic)[sapply(BusinessAnalytic, class) %in% c("integer",
"numeric")] # get numeric var names
num.Full.DS <- BusinessAnalytic[, numericvars] # get only numeric variables
cor.Full.DS <- data.frame(round(cor(num.Full.DS), 2))
cor.Full.DS
cores <- cor(num.Full.DS, use = "complete.obs")
round(cores, 2)
library(corrplot)
corrplot(cores, type = "upper", order = "hclust",
tl.col = "black", tl.srt = 45)
#### Feature creation: Create Four new features that may have predictive power.
BusinessAnalytic$combine.alc <- BusinessAnalytic$Dalc * BusinessAnalytic$Walc
BusinessAnalytic$combine.education <- BusinessAnalytic$Medu * BusinessAnalytic$Fedu
BusinessAnalytic$both.college <- ifelse(BusinessAnalytic$combine.education == 16, 1, 0)
BusinessAnalytic$failures.flag <- ifelse(BusinessAnalytic$failures > 0, 1, 0)
#Splitting data into training and test sets
library(caTools) # The splitting library
library(caret)
set.seed(200) # set seed to ensure you always have same random numbers generated
datak<- createDataPartition(BusinessAnalytic$G3.Pass.Flag, list = FALSE, p = .75)
traindata <- BusinessAnalytic[datak, ]
testdata <- BusinessAnalytic[-datak, ]
# Pass Rates in train set:
table(traindata $G3.Pass.Flag) / nrow(traindata)
# Pass rates in test set:
table(testdata $G3.Pass.Flag) / nrow(testdata )
##Building Models
library(sjPlot)
##Generalized Least Squares Model
formula <- as.formula(G3.Pass.Flag ~ goout + combine.education + failures + Medu +
failures.flag+
internet + famsup + Mjob + Fedu + health)
GLM <- glm(formula, data = traindata, family = binomial(link = "logit"))
library(sjPlot)
summary(GLM)
summary(GLM)
summary(traindata$Mjob)
#Relevel Mjob to make services the base.

22
traindata$Mjob<-as.factor(traindata$Mjob)
testdata$Mjob <-as.factor(testdata$Mjob )
levels(traindata$Mjob)
traindata$Mjob <- relevel(traindata$Mjob, ref = "services")
levels(traindata$Mjob)
testdata$Mjob <- relevel(testdata$Mjob, ref = "services")
#Rerun the GLM with the smaller set of variables.
formula <- as.formula(G3.Pass.Flag~goout + failures + Medu +
internet + famsup + Mjob + health)
GLM <- glm(formula, data = traindata, family = binomial(link = "logit"))
summary(GLM)
###We need to look at Mjob. First determine which level has the most observations
cutoff <- 0.5 # set cutoff value
print("Training confusion matrix")
predicted <- predict(GLM, type = "response") #This outputs the probabiity of passing
predicted.final <- as.factor(ifelse(predicted > cutoff, "P", "F"))
confusionMatrix(predicted.final, factor(traindata$G3.Pass.Flag))
print("Testing confusion matrix")
predicted <- predict(GLM, newdata = testdata, type = "response") # This outputs the probabiity
of passing
predicted.final <- as.factor(ifelse(predicted > cutoff, "P", "F"))
confusionMatrix(predicted.final, factor(testdata$G3.Pass.Flag))
#Use stepAIC from the MASS package (drop1 could also be employed) to see which variables
could be removed.
library(MASS)
stepAIC(GLM, direction = "backward")
cutoff <- 0.5 # set cutoff value
print("Training confusion matrix")
predicted <- predict(GLM, type = "response") # This outputs the probabiity of passing
predicted.final <- as.factor(ifelse(predicted > cutoff, "P", "F"))
confusionMatrix(predicted.final, factor(traindata$G3.Pass.Flag))
print("Testing Confusion Matrix")
predicted <- predict(GLM, newdata = testdata, type = "response") # This outputs the probabiity
of passing
predicted.final <- as.factor(ifelse(predicted > cutoff, "P", "F"))
confusionMatrix(predicted.final, factor(testdata$G3.Pass.Flag))
##Decision Trees
library(rpart) # R package for decision Tree
library(rpart.plot)
set.seed(200)
excluded_variables <- c("G1","G2")
dt <- rpart(G3.Pass.Flag ~ .,
data = traindata[, !(names(BusinessAnalytic) %in% excluded_variables)],
control = rpart.control(minbucket = 10, cp = .1, maxdepth = 30),
parms = list(split = "gini"))
rpart.plot(dt,roundint=FALSE)

23
cutoff <- 0.5
print("Train confusion matrix")
predicted <- predict(dt, type = "prob")[,1] # This outputs the probability of failing
predicted.final <- as.factor(ifelse(predicted > cutoff, "F", "P"))
confusionMatrix(predicted.final, factor(traindata$G3.Pass.Flag))
print("Test confusion matrix")
predicted <- predict(dt, newdata = testdata, type = "prob")[,1] # This outputs the probability of
failing
predicted.final <- as.factor(ifelse(predicted > cutoff, "F", "P"))
confusionMatrix(predicted.final, factor(testdata$G3.Pass.Flag))
#Changing parameters
dt <- rpart(G3.Pass.Flag ~ .,
data = traindata[, !(names( BusinessAnalytic ) %in% excluded_variables)],
control = rpart.control(minbucket = 50, cp = 0.2, maxdepth = 10),
parms = list(split = "gini"))
rpart.plot(dt)
cutoff <- 0.8
print("Train confusion matrix")
predicted <- predict(dt, type = "prob")[,1] # This outputs the probability of failing
predicted.final <- as.factor(ifelse(predicted > cutoff, "F", "P"))
confusionMatrix(predicted.final, factor(traindata$G3.Pass.Flag))
#Random Forest
library(randomForest)
# Create a Random Forest model with default parameters
summary(traindata)
set.seed(100)
excluded_variables <- c("address")
control <- trainControl(method = "repeatedcv", number = 5, repeats = 2)
tune_grid <- expand.grid(mtry = c(15:25))
rf <- train(as.factor(G3.Pass.Flag) ~ .,
data = traindata[, !(names(traindata) %in% excluded_variables)], method = "rf", ntree =
50, importance = TRUE, trControl = control, tuneGrid = tune_grid)
plot(rf)
plot(varImp(rf), top = 15, main = "Variable Importance of Classification Random Forest")
cutoff <- 0.5 # set cutoff value
print("Training confusion matrix")
predicted <- predict(rf, type = "prob")[,1] # This outputs the probabiity of failing
predicted.final <- as.factor(ifelse(predicted > cutoff, "F", "P"))
confusionMatrix(predicted.final, factor(traindata$G3.Pass.Flag))
print("Testing confusion matrix")
predicted <- predict(rf, newdata = testdata, type = "prob")[,1] # This outputs the probabiity of
failing
predicted.final <- as.factor(ifelse(predicted > cutoff, "F", "P"))
confusionMatrix(predicted.final, factor(testdata$G3.Pass.Flag))