Deakin University MAF308 Assignment 2: Bond Valuation and Analysis
VerifiedAdded on 2022/11/30
|11
|1649
|416
Homework Assignment
AI Summary
This assignment solution for MAF308, Derivatives and Fixed Income Securities, analyzes a bond issued by a company, calculating its yield to maturity (YTM) and comparing it to the market price. The solution provides a detailed calculation of YTM, considering the coupon rate, face value, and redemption date, and highlights the difference between approximate and IRR methods for YTM calculation. Furthermore, the assignment includes a bond valuation analysis, demonstrating how to determine the bond's present value and price based on its cash flows. It then constructs graphs illustrating the relationship between bond price and YTM, both annualized and semi-annualized, and calculates the bond's duration, which measures its price sensitivity to interest rate changes. The solution also references relevant literature to support the analysis, providing a comprehensive understanding of bond valuation and related concepts.

MAF308
0
0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

A1
Face value of bond issued by company= $100
Market price = $127.62
Date of Redemption = 21/4/27
Coupon Rate of bond which is also known as interest rate = 4.75 percent per annum (semi-
annually arrears)
Redeemable at par
Computation of yield to maturity as on 0/07/19
interest amount+ redemption value-market price
X 100
no. of times
redemption value+market price
2
2.375+ 100-127.62
= 15.611 X 100
100+127.62
X 100= 2.375-1.7693
11.3.81
= 0.5332% (semi-annually)
= 1.0644% annually (per annum)
Note: 1 calculation of interest amount
Interest amount = face value X 4.75% X 6/12
= 100 X 4.75% X 6/12
1
Face value of bond issued by company= $100
Market price = $127.62
Date of Redemption = 21/4/27
Coupon Rate of bond which is also known as interest rate = 4.75 percent per annum (semi-
annually arrears)
Redeemable at par
Computation of yield to maturity as on 0/07/19
interest amount+ redemption value-market price
X 100
no. of times
redemption value+market price
2
2.375+ 100-127.62
= 15.611 X 100
100+127.62
X 100= 2.375-1.7693
11.3.81
= 0.5332% (semi-annually)
= 1.0644% annually (per annum)
Note: 1 calculation of interest amount
Interest amount = face value X 4.75% X 6/12
= 100 X 4.75% X 6/12
1

= 2.375
Note2: calculation of “n” (number of times/periods)
n= 03/07/19 to 21/4/27
=2849 days
= 2849/182.5
= 15.611
[Number of days in a year = 365 days]
Number of days in 6 months = 365/2
= 182.5 days
The yield to maturity which has been provided in the corresponding column is 1.164 percent per
annum and the actual yield to maturity which has been calculated comes to 1.0644% p.a. There
is a slight difference between these two rates. The reason behind the differences is that there are
two formulas for calculating the yield to maturity one is an internal rate of return that is IRR and
the other one is that has been used in the above calculation to calculate YTM. The method which
has been applied in this paper gives approximate result and the other method which is also
known as the IRR method gives an accurate result. In the IRR method, the yield to maturity is
calculated by adjusting the expected rate of return and this adjustment is done to equals the
present value of the bond with the bond price. Both the method use current market price of the
bond. The formula which gives approx result does not consider present value of the bond while
the IRR method which gives exact YTM use present value by using discounting factor.
2
Note2: calculation of “n” (number of times/periods)
n= 03/07/19 to 21/4/27
=2849 days
= 2849/182.5
= 15.611
[Number of days in a year = 365 days]
Number of days in 6 months = 365/2
= 182.5 days
The yield to maturity which has been provided in the corresponding column is 1.164 percent per
annum and the actual yield to maturity which has been calculated comes to 1.0644% p.a. There
is a slight difference between these two rates. The reason behind the differences is that there are
two formulas for calculating the yield to maturity one is an internal rate of return that is IRR and
the other one is that has been used in the above calculation to calculate YTM. The method which
has been applied in this paper gives approximate result and the other method which is also
known as the IRR method gives an accurate result. In the IRR method, the yield to maturity is
calculated by adjusting the expected rate of return and this adjustment is done to equals the
present value of the bond with the bond price. Both the method use current market price of the
bond. The formula which gives approx result does not consider present value of the bond while
the IRR method which gives exact YTM use present value by using discounting factor.
2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
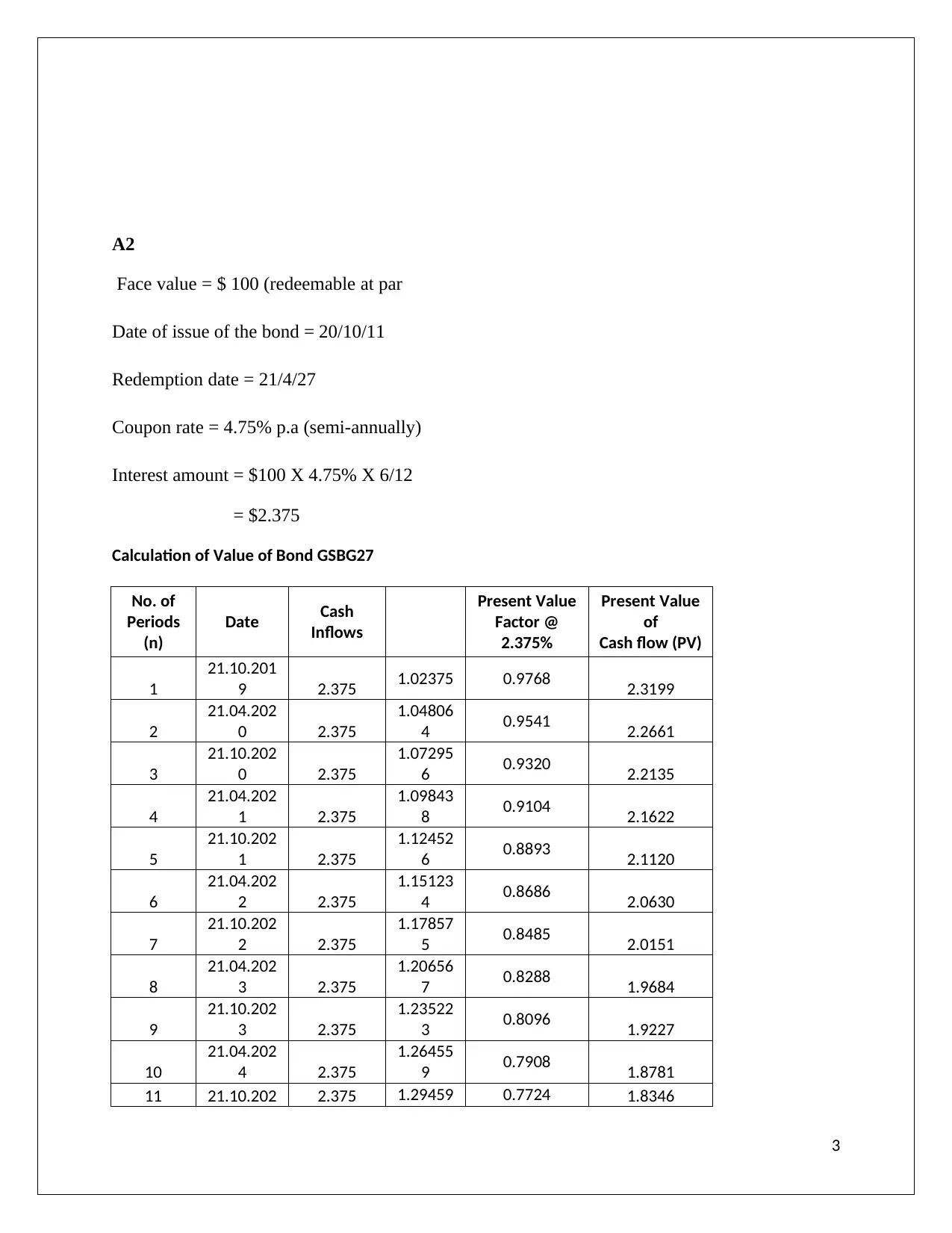
A2
Face value = $ 100 (redeemable at par
Date of issue of the bond = 20/10/11
Redemption date = 21/4/27
Coupon rate = 4.75% p.a (semi-annually)
Interest amount = $100 X 4.75% X 6/12
= $2.375
Calculation of Value of Bond GSBG27
No. of
Periods
(n)
Date Cash
Inflows
Present Value
Factor @
2.375%
Present Value
of
Cash flow (PV)
1
21.10.201
9 2.375 1.02375 0.9768 2.3199
2
21.04.202
0 2.375
1.04806
4 0.9541 2.2661
3
21.10.202
0 2.375
1.07295
6 0.9320 2.2135
4
21.04.202
1 2.375
1.09843
8 0.9104 2.1622
5
21.10.202
1 2.375
1.12452
6 0.8893 2.1120
6
21.04.202
2 2.375
1.15123
4 0.8686 2.0630
7
21.10.202
2 2.375
1.17857
5 0.8485 2.0151
8
21.04.202
3 2.375
1.20656
7 0.8288 1.9684
9
21.10.202
3 2.375
1.23522
3 0.8096 1.9227
10
21.04.202
4 2.375
1.26455
9 0.7908 1.8781
11 21.10.202 2.375 1.29459 0.7724 1.8346
3
Face value = $ 100 (redeemable at par
Date of issue of the bond = 20/10/11
Redemption date = 21/4/27
Coupon rate = 4.75% p.a (semi-annually)
Interest amount = $100 X 4.75% X 6/12
= $2.375
Calculation of Value of Bond GSBG27
No. of
Periods
(n)
Date Cash
Inflows
Present Value
Factor @
2.375%
Present Value
of
Cash flow (PV)
1
21.10.201
9 2.375 1.02375 0.9768 2.3199
2
21.04.202
0 2.375
1.04806
4 0.9541 2.2661
3
21.10.202
0 2.375
1.07295
6 0.9320 2.2135
4
21.04.202
1 2.375
1.09843
8 0.9104 2.1622
5
21.10.202
1 2.375
1.12452
6 0.8893 2.1120
6
21.04.202
2 2.375
1.15123
4 0.8686 2.0630
7
21.10.202
2 2.375
1.17857
5 0.8485 2.0151
8
21.04.202
3 2.375
1.20656
7 0.8288 1.9684
9
21.10.202
3 2.375
1.23522
3 0.8096 1.9227
10
21.04.202
4 2.375
1.26455
9 0.7908 1.8781
11 21.10.202 2.375 1.29459 0.7724 1.8346
3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4 2
12
21.04.202
5 2.375
1.32533
9 0.7545 1.7920
13
21.10.202
5 2.375
1.35681
6 0.7370 1.7504
14
21.04.202
6 2.375 1.38904 0.7199 1.7098
15
21.10.202
6 2.375 1.42203 0.7032 1.6701
16
21.04.202
7 2.375
1.45580
3 0.6869 1.6314
16
21.04.202
7 100
1.45580
3 0.6869 68.6906
Valuation Price of the Bond: 100.00
In this paper the statement given is correct and also the calculation is correct. When the interest
rate of the bond the rate of return of the bond is the same then it can be said that the company has
issued the bond at par that is without any discount or premium. In the above calculation, the
interest rate and yield rate are the same and the same rate has been used for compounding and
discounting the bond. So the face value of the securities at the time of the issue will become the
maturity price of the bond. The present value of the interest and redemption value of the bond
will be the same as face value of bond.
A3
Construction of graph showing relationship between bond and yield to maturity
Yield Rate
(Annualized
)
(in %)
Bond
Price
($)
0% 138.00
0.50% 133.25
1.0% 128.69
1.5% 124.33
2.0% 120.15
2.5% 116.13
3.0% 112.28
3.5% 108.59
4
12
21.04.202
5 2.375
1.32533
9 0.7545 1.7920
13
21.10.202
5 2.375
1.35681
6 0.7370 1.7504
14
21.04.202
6 2.375 1.38904 0.7199 1.7098
15
21.10.202
6 2.375 1.42203 0.7032 1.6701
16
21.04.202
7 2.375
1.45580
3 0.6869 1.6314
16
21.04.202
7 100
1.45580
3 0.6869 68.6906
Valuation Price of the Bond: 100.00
In this paper the statement given is correct and also the calculation is correct. When the interest
rate of the bond the rate of return of the bond is the same then it can be said that the company has
issued the bond at par that is without any discount or premium. In the above calculation, the
interest rate and yield rate are the same and the same rate has been used for compounding and
discounting the bond. So the face value of the securities at the time of the issue will become the
maturity price of the bond. The present value of the interest and redemption value of the bond
will be the same as face value of bond.
A3
Construction of graph showing relationship between bond and yield to maturity
Yield Rate
(Annualized
)
(in %)
Bond
Price
($)
0% 138.00
0.50% 133.25
1.0% 128.69
1.5% 124.33
2.0% 120.15
2.5% 116.13
3.0% 112.28
3.5% 108.59
4

4.0% 105.05
4.5% 101.65
5.0% 98.38
5.5% 95.25
6.0% 92.24
6.5% 89.34
7.0% 86.56
7.5% 83.89
8.0% 81.32
0% 1% 2% 3% 4% 5% 6% 7% 8% 9%
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
Bond Price
($)
Figure no. 1: Relationship between YTM and price of the bond (Annualized)
Yield Rate
(Semi-
annualized)
(in %)
Bond Price
($)
0% 138.00
0.50% 128.76
1.0% 120.24
1.5% 112.36
2.0% 105.09
2.5% 98.37
3.0% 92.15
3.5% 86.39
4.0% 81.07
4.5% 76.13
5
4.5% 101.65
5.0% 98.38
5.5% 95.25
6.0% 92.24
6.5% 89.34
7.0% 86.56
7.5% 83.89
8.0% 81.32
0% 1% 2% 3% 4% 5% 6% 7% 8% 9%
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
Bond Price
($)
Figure no. 1: Relationship between YTM and price of the bond (Annualized)
Yield Rate
(Semi-
annualized)
(in %)
Bond Price
($)
0% 138.00
0.50% 128.76
1.0% 120.24
1.5% 112.36
2.0% 105.09
2.5% 98.37
3.0% 92.15
3.5% 86.39
4.0% 81.07
4.5% 76.13
5
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
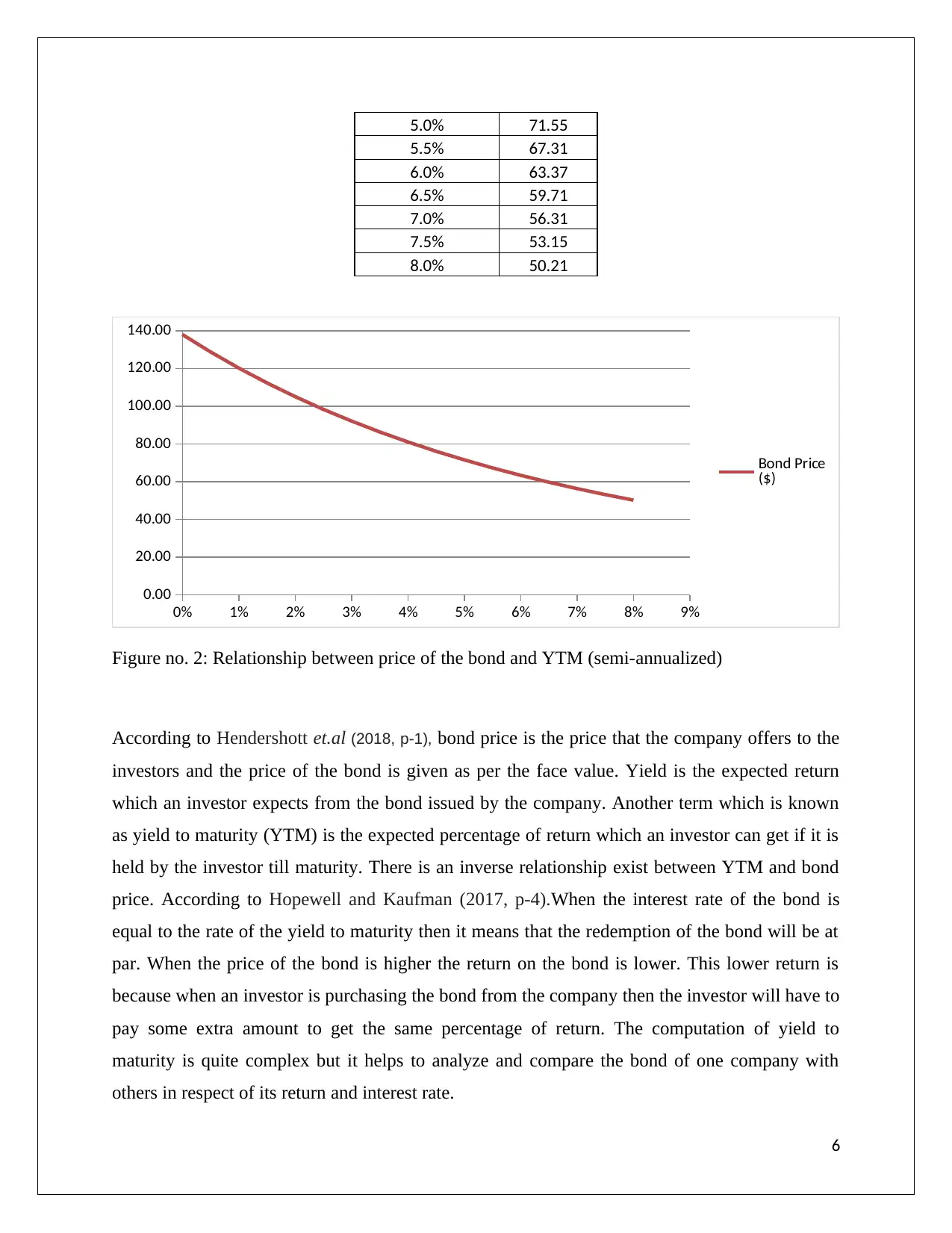
5.0% 71.55
5.5% 67.31
6.0% 63.37
6.5% 59.71
7.0% 56.31
7.5% 53.15
8.0% 50.21
0% 1% 2% 3% 4% 5% 6% 7% 8% 9%
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
Bond Price
($)
Figure no. 2: Relationship between price of the bond and YTM (semi-annualized)
According to Hendershott et.al (2018, p-1), bond price is the price that the company offers to the
investors and the price of the bond is given as per the face value. Yield is the expected return
which an investor expects from the bond issued by the company. Another term which is known
as yield to maturity (YTM) is the expected percentage of return which an investor can get if it is
held by the investor till maturity. There is an inverse relationship exist between YTM and bond
price. According to Hopewell and Kaufman (2017, p-4).When the interest rate of the bond is
equal to the rate of the yield to maturity then it means that the redemption of the bond will be at
par. When the price of the bond is higher the return on the bond is lower. This lower return is
because when an investor is purchasing the bond from the company then the investor will have to
pay some extra amount to get the same percentage of return. The computation of yield to
maturity is quite complex but it helps to analyze and compare the bond of one company with
others in respect of its return and interest rate.
6
5.5% 67.31
6.0% 63.37
6.5% 59.71
7.0% 56.31
7.5% 53.15
8.0% 50.21
0% 1% 2% 3% 4% 5% 6% 7% 8% 9%
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
Bond Price
($)
Figure no. 2: Relationship between price of the bond and YTM (semi-annualized)
According to Hendershott et.al (2018, p-1), bond price is the price that the company offers to the
investors and the price of the bond is given as per the face value. Yield is the expected return
which an investor expects from the bond issued by the company. Another term which is known
as yield to maturity (YTM) is the expected percentage of return which an investor can get if it is
held by the investor till maturity. There is an inverse relationship exist between YTM and bond
price. According to Hopewell and Kaufman (2017, p-4).When the interest rate of the bond is
equal to the rate of the yield to maturity then it means that the redemption of the bond will be at
par. When the price of the bond is higher the return on the bond is lower. This lower return is
because when an investor is purchasing the bond from the company then the investor will have to
pay some extra amount to get the same percentage of return. The computation of yield to
maturity is quite complex but it helps to analyze and compare the bond of one company with
others in respect of its return and interest rate.
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
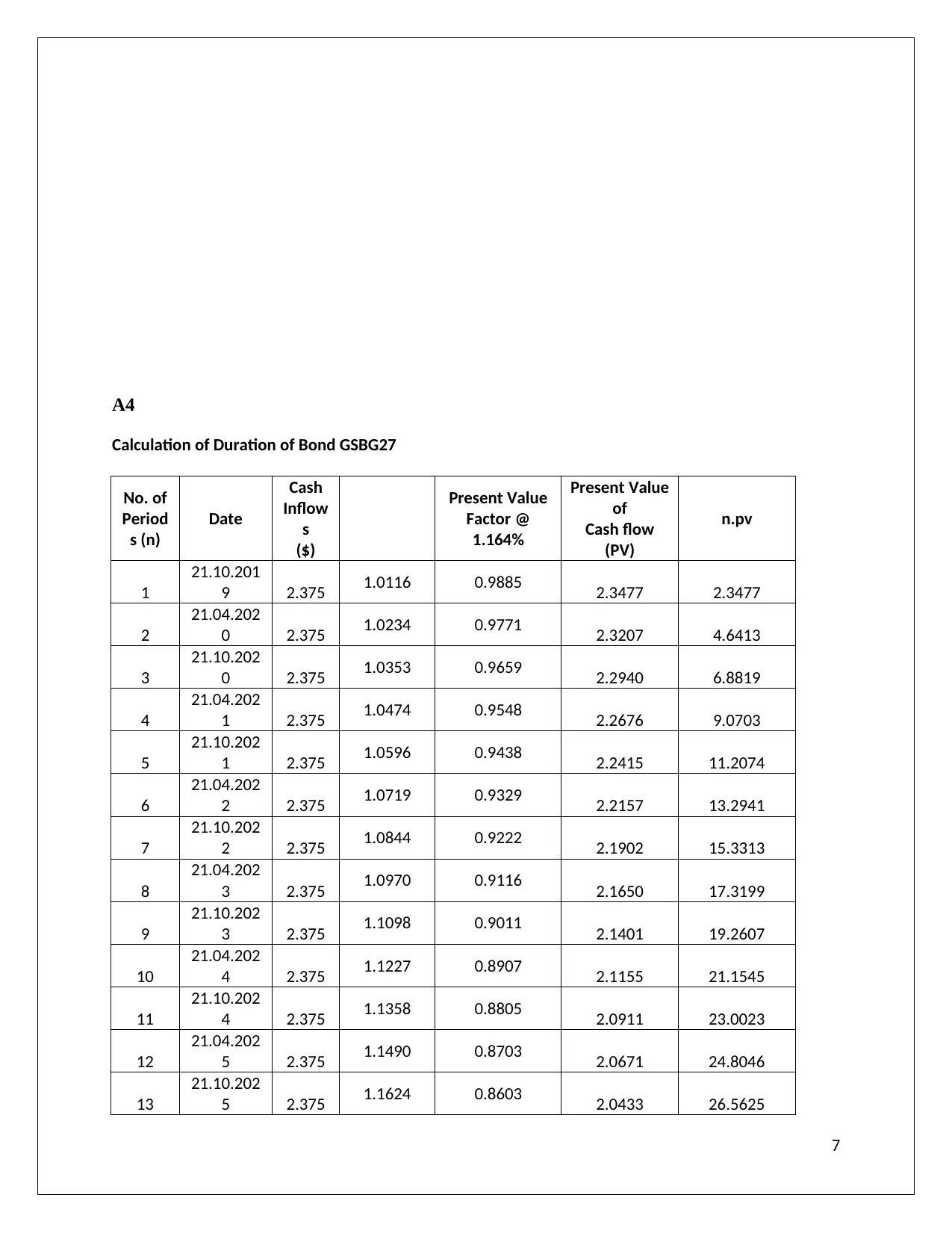
A4
Calculation of Duration of Bond GSBG27
No. of
Period
s (n)
Date
Cash
Inflow
s
($)
Present Value
Factor @
1.164%
Present Value
of
Cash flow
(PV)
n.pv
1
21.10.201
9 2.375 1.0116 0.9885 2.3477 2.3477
2
21.04.202
0 2.375 1.0234 0.9771 2.3207 4.6413
3
21.10.202
0 2.375 1.0353 0.9659 2.2940 6.8819
4
21.04.202
1 2.375 1.0474 0.9548 2.2676 9.0703
5
21.10.202
1 2.375 1.0596 0.9438 2.2415 11.2074
6
21.04.202
2 2.375 1.0719 0.9329 2.2157 13.2941
7
21.10.202
2 2.375 1.0844 0.9222 2.1902 15.3313
8
21.04.202
3 2.375 1.0970 0.9116 2.1650 17.3199
9
21.10.202
3 2.375 1.1098 0.9011 2.1401 19.2607
10
21.04.202
4 2.375 1.1227 0.8907 2.1155 21.1545
11
21.10.202
4 2.375 1.1358 0.8805 2.0911 23.0023
12
21.04.202
5 2.375 1.1490 0.8703 2.0671 24.8046
13
21.10.202
5 2.375 1.1624 0.8603 2.0433 26.5625
7
Calculation of Duration of Bond GSBG27
No. of
Period
s (n)
Date
Cash
Inflow
s
($)
Present Value
Factor @
1.164%
Present Value
of
Cash flow
(PV)
n.pv
1
21.10.201
9 2.375 1.0116 0.9885 2.3477 2.3477
2
21.04.202
0 2.375 1.0234 0.9771 2.3207 4.6413
3
21.10.202
0 2.375 1.0353 0.9659 2.2940 6.8819
4
21.04.202
1 2.375 1.0474 0.9548 2.2676 9.0703
5
21.10.202
1 2.375 1.0596 0.9438 2.2415 11.2074
6
21.04.202
2 2.375 1.0719 0.9329 2.2157 13.2941
7
21.10.202
2 2.375 1.0844 0.9222 2.1902 15.3313
8
21.04.202
3 2.375 1.0970 0.9116 2.1650 17.3199
9
21.10.202
3 2.375 1.1098 0.9011 2.1401 19.2607
10
21.04.202
4 2.375 1.1227 0.8907 2.1155 21.1545
11
21.10.202
4 2.375 1.1358 0.8805 2.0911 23.0023
12
21.04.202
5 2.375 1.1490 0.8703 2.0671 24.8046
13
21.10.202
5 2.375 1.1624 0.8603 2.0433 26.5625
7

14
21.04.202
6 2.375 1.1759 0.8504 2.0198 28.2766
15
21.10.202
6 2.375 1.1896 0.8406 1.9965 29.9478
16
21.04.202
7 2.375 1.2034 0.8310 1.9735 31.5768
16
21.04.202
7 100 1.2034 0.8310 83.0968 1329.5482
Intrinsic Value of Bond: 117.5858 1614.2279
Duration of the bond= ∑ n.pv
Intrinsic Value
= 1614.2279
117.5858
= 13.7281
X
Y
8
Coupon Rate/YTM
Dur
atio
n of
Bon
d
21.04.202
6 2.375 1.1759 0.8504 2.0198 28.2766
15
21.10.202
6 2.375 1.1896 0.8406 1.9965 29.9478
16
21.04.202
7 2.375 1.2034 0.8310 1.9735 31.5768
16
21.04.202
7 100 1.2034 0.8310 83.0968 1329.5482
Intrinsic Value of Bond: 117.5858 1614.2279
Duration of the bond= ∑ n.pv
Intrinsic Value
= 1614.2279
117.5858
= 13.7281
X
Y
8
Coupon Rate/YTM
Dur
atio
n of
Bon
d
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Figure no. 3 Relationship between duration of bond and coupon rate/ yield to maturity
As it can be seen that the present value of the bond comes to 117.5858 and when the intrinsic
value is multiplied by the no. of periods the intrinsic value increases to 1614.2279. The intrinsic
value has been calculated by multiplying the discounting factor with the cash inflow of the bond.
The duration of bond as per the above calculation comes to 13.7821. The number of periods
which has been taken to calculate the duration is 16 and a discounting factor of 1.164 percent has
been used. The company or the investor measure the duration of bond so that they can measures
the sensitivity of the price of bond with changes in coupon rate of bond. As per the graph, the
duration of bond is 13 which represents that the bond will take this much of time to earn half of
the intrinsic value which will come from the bond. As can be seen in the graph that when the
coupon rate is higher the duration and the risk related to the interest rate is lower and vice-versa.
9
As it can be seen that the present value of the bond comes to 117.5858 and when the intrinsic
value is multiplied by the no. of periods the intrinsic value increases to 1614.2279. The intrinsic
value has been calculated by multiplying the discounting factor with the cash inflow of the bond.
The duration of bond as per the above calculation comes to 13.7821. The number of periods
which has been taken to calculate the duration is 16 and a discounting factor of 1.164 percent has
been used. The company or the investor measure the duration of bond so that they can measures
the sensitivity of the price of bond with changes in coupon rate of bond. As per the graph, the
duration of bond is 13 which represents that the bond will take this much of time to earn half of
the intrinsic value which will come from the bond. As can be seen in the graph that when the
coupon rate is higher the duration and the risk related to the interest rate is lower and vice-versa.
9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

References
Hendershott, T., Kozhan, R. and Raman, V., (2018). Short selling and price discovery in
corporate bonds. Journal of Financial and Quantitative Analysis, pp.1-80.
Hopewell, M.H. and Kaufman, G.G., (2017). Bond price volatility and term to maturity: A
generalized respecification. In Bond Duration and Immunization (pp. 64-68). Routledge.
10
Hendershott, T., Kozhan, R. and Raman, V., (2018). Short selling and price discovery in
corporate bonds. Journal of Financial and Quantitative Analysis, pp.1-80.
Hopewell, M.H. and Kaufman, G.G., (2017). Bond price volatility and term to maturity: A
generalized respecification. In Bond Duration and Immunization (pp. 64-68). Routledge.
10
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.