Managerial Accounting: Portfolio Return, Risk & CAPM Analysis

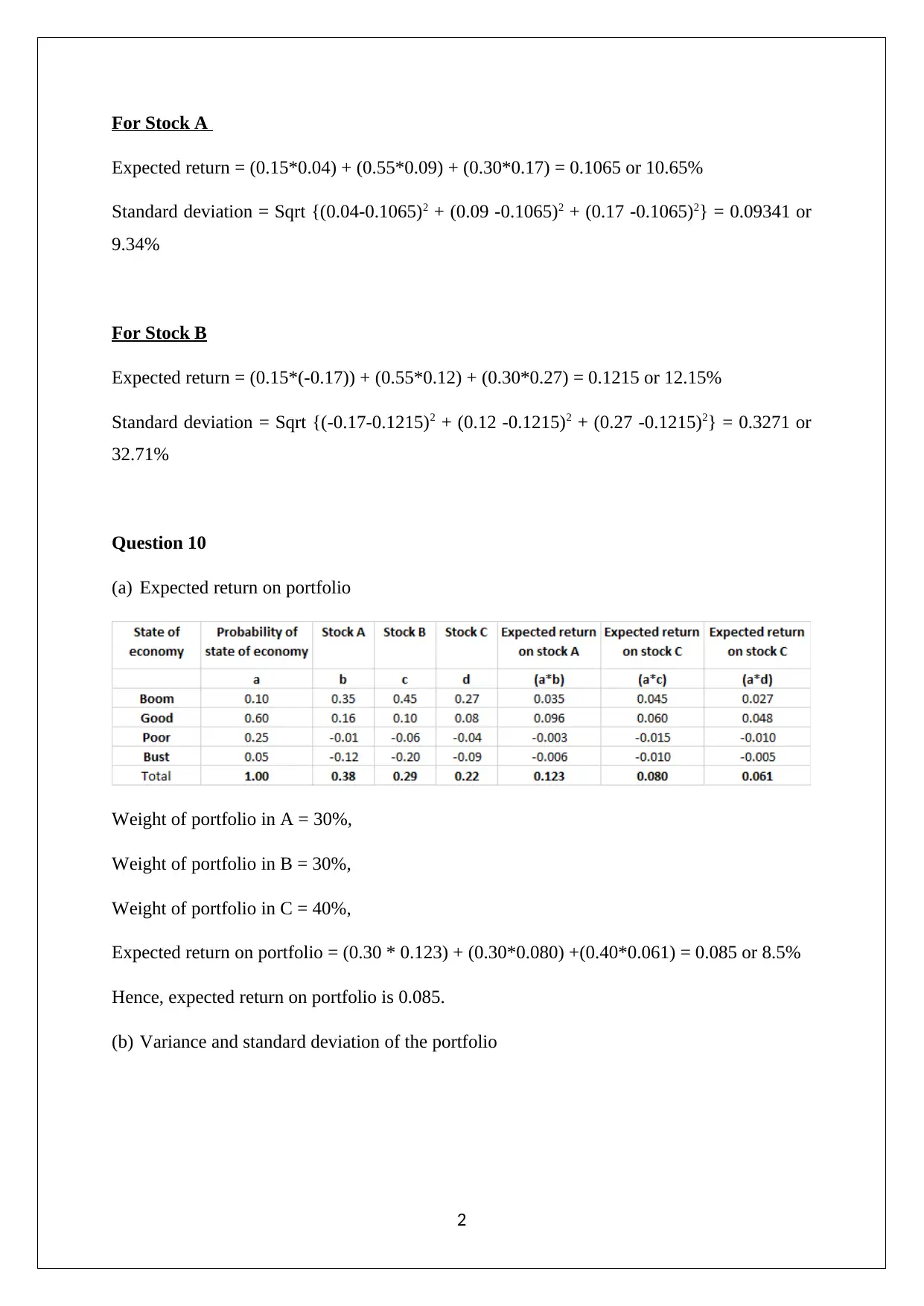
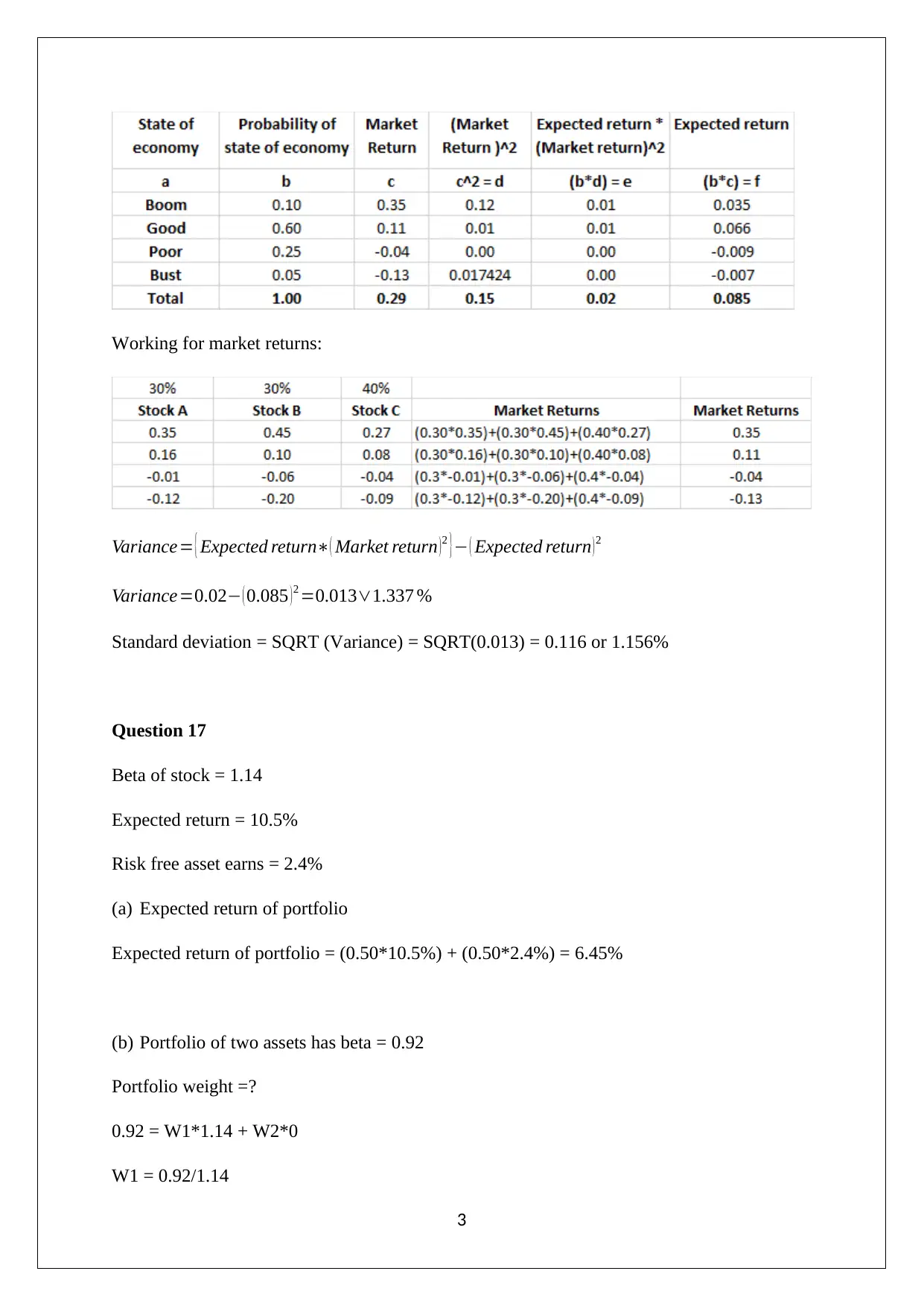
This assignment provides solutions to problems related to portfolio expected return, standard deviation, and the Capital Asset Pricing Model (CAPM). It includes calculations for determining the amount to invest in different stocks to achieve a target portfolio return, computing expected returns and standard deviations for stocks under various economic scenarios, and analyzing portfolio risk and return using CAPM principles. The problems cover topics such as calculating portfolio weights, determining portfolio beta, and assessing the impact of risk-free assets on portfolio performance, offering a comprehensive overview of key concepts in financial management and investment analysis. Desklib provides this document and many others to help students excel.

Managerial accounting
Assignment
[DATE]
STUDENT ID
STUDENT NAME

Question 4
Portfolio expected return = $10,000
Expected return of stock X = 11.5%
Expected return of stock Y = 9.4%
Expected return portfolio = 10.85%
Money invest in stock X and stock Y =?
Weight of stock X is Wx and stock Y is Wy.
Now,
0.1085 = (0.115*Wx) +(0.094*Wy)
0.1085 = (0.115*Wx) +(0.094*(1-Wx)
Wx = 0.690476
Wy = 1 – Wx = 1-0.690476 = 0.3095
Now,
Question 7
Expected return and standard deviation of stock A and B
State of
Economy
Probability of State of
Economy
Rate of Return if State
Occurs
Stock A Stock B
Recession .15 .04 −.17
Normal .55 .09 .12
Boom .30 .17 .27
1

For Stock A
Expected return = (0.15*0.04) + (0.55*0.09) + (0.30*0.17) = 0.1065 or 10.65%
Standard deviation = Sqrt {(0.04-0.1065)2 + (0.09 -0.1065)2 + (0.17 -0.1065)2} = 0.09341 or
9.34%
For Stock B
Expected return = (0.15*(-0.17)) + (0.55*0.12) + (0.30*0.27) = 0.1215 or 12.15%
Standard deviation = Sqrt {(-0.17-0.1215)2 + (0.12 -0.1215)2 + (0.27 -0.1215)2} = 0.3271 or
32.71%
Question 10
(a) Expected return on portfolio
Weight of portfolio in A = 30%,
Weight of portfolio in B = 30%,
Weight of portfolio in C = 40%,
Expected return on portfolio = (0.30 * 0.123) + (0.30*0.080) +(0.40*0.061) = 0.085 or 8.5%
Hence, expected return on portfolio is 0.085.
(b) Variance and standard deviation of the portfolio
2

Working for market returns:
Variance= { Expected return∗( Market return )2 }− ( Expected return )2
Variance=0.02− ( 0.085 ) 2 =0.013∨1.337 %
Standard deviation = SQRT (Variance) = SQRT(0.013) = 0.116 or 1.156%
Question 17
Beta of stock = 1.14
Expected return = 10.5%
Risk free asset earns = 2.4%
(a) Expected return of portfolio
Expected return of portfolio = (0.50*10.5%) + (0.50*2.4%) = 6.45%
(b) Portfolio of two assets has beta = 0.92
Portfolio weight =?
0.92 = W1*1.14 + W2*0
W1 = 0.92/1.14
3

W1=0.8070
W2 = 1-0.8070 = 0.193
(c) Expected return of portfolio = 9%
Beta =?
9% = W1*10.5% + (1-W1) * 2.4%
W1 = 0.8148
W2 =1-W1
W2= 1-0.8148 = 0.1852
Hence,
Portfolio beta = (0.8148*1.14) + (0.1852*0) = 0.93
(d) Portfolio of two assets has beta = 2.28
Portfolio weights =?
2.28 = W1*1.14 +W2*0
W1 = 2.28/1.14 = 2
W2 = 1-W1= 1-2 = -1
4

5