MAP4C - Financial Math: Lesson Assignment 18 - Mortgage Applications

This assignment focuses on mortgage calculations and analysis, providing solutions to various problems related to fixed-rate mortgages. The document calculates monthly payments, total amounts paid, total principal and interest, and the value of a house after appreciation. It also explores amortization tables, determining debt owed, and the impact of down payments and amortization periods on mortgage amounts. The assignment covers scenarios involving different interest rates, amortization periods, and loan amounts, providing a comprehensive understanding of mortgage-related financial concepts. The solutions include detailed explanations of the strategies used to arrive at the answers, often referencing the formulas and methods used in financial mathematics, and the use of tools such as Excel. The assignment covers key aspects of mortgage calculations, including the impact of interest rates, amortization periods, and down payments on the overall cost of a mortgage, making it a valuable resource for students studying financial mathematics.

MAP4C Lesson Assignment 18
In this assignment you are going to focus on: Mortgages.
Total Marks: 64 marks
Instructions:
After completing the lesson action section of your home page, you are ready to complete your lesson assignment. Follow
these steps.
a) In the textbox given, explain the strategy that you used to determine your answer.
b) Fill in your answer. The mark for each question is given at the introduction to the questions to be completed.
c) When finished answering all your questions, save your file and upload the file into the appropriate dropbox.
Part A (Putting the Concepts to Work): Completion (64 marks): Using your reading, answer the following
questions. Give your answer as well as your strategy for determining your answer. As part of your answer, give the page
number in the reference material or the website that you used to find the answer to the question.
1. (four marks) Determine the monthly payment for a five-year fixed rate mortgage of $260 000 amortized over
25 years at an annual interest rate of 6.49%.
Here, P = 260000 , r = 6.49 % , n = 12 , Y = 25
PMT = ( P∗r
n )/ [1−(1+ r
n )−nY
]
Putting the respective values and solving in Excel we get
PMT = $1753.91
2. (four marks) Calculate the total amount paid over the term of a five-year fixed rate mortgage of $260 000
amortized over 25 years at an annual interest rate of 6.49%.
Here, P = 260000 , r = 6.49 % , n = 12 , Y = 5
PMT = ( P∗r
n )/ [ 1−( 1+ r
n )
−nY
]
Putting the respective values and solving in Excel we get
PMT = $1753.91
Total amount paid: 1753.91*12*25 = $ 526173
MAP4C Lesson Assignment Page 1

3. (four marks) Calculate the total principal paid over the term of a five-year fixed rate mortgage of $260 000
amortized over 25 years at an annual interest rate of 6.49%.
Total principal paid: $260000
4. (four marks) Calculate the total interest paid over the term of a five-year fixed rate mortgage of $260 000
amortized over 25 years at an annual interest rate of 6.49%.
Total interest paid : ($ 526173 - $260000) = $266173
5. (four marks) Calculate the approximate value of a $260 000 house after five years if it has an appreciation
rate of 6% per year.
MAP4C Lesson Assignment Page 2

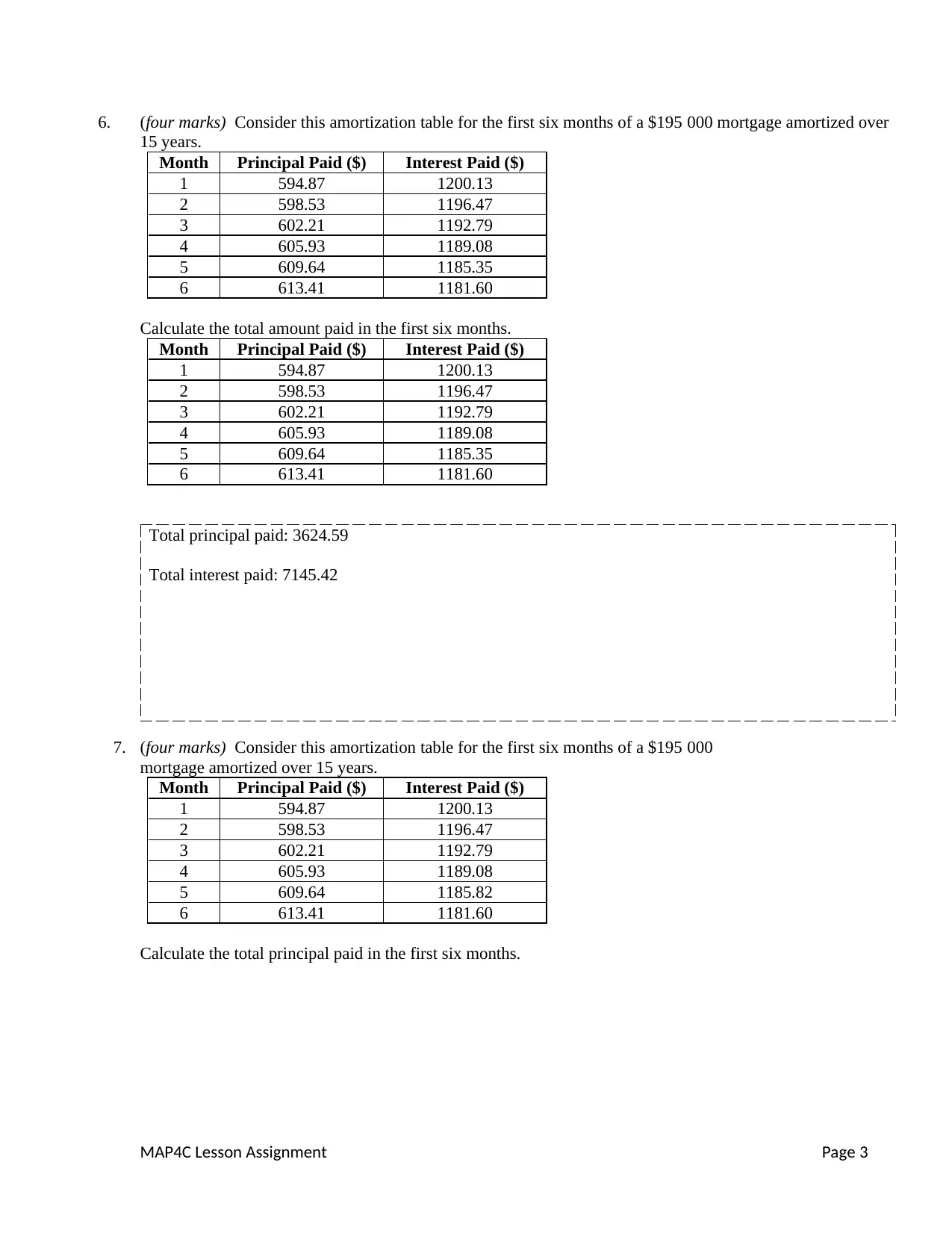
6. (four marks) Consider this amortization table for the first six months of a $195 000 mortgage amortized over
15 years.
Month Principal Paid ($) Interest Paid ($)
1 594.87 1200.13
2 598.53 1196.47
3 602.21 1192.79
4 605.93 1189.08
5 609.64 1185.35
6 613.41 1181.60
Calculate the total amount paid in the first six months.
Month Principal Paid ($) Interest Paid ($)
1 594.87 1200.13
2 598.53 1196.47
3 602.21 1192.79
4 605.93 1189.08
5 609.64 1185.35
6 613.41 1181.60
Total principal paid: 3624.59
Total interest paid: 7145.42
7. (four marks) Consider this amortization table for the first six months of a $195 000
mortgage amortized over 15 years.
Month Principal Paid ($) Interest Paid ($)
1 594.87 1200.13
2 598.53 1196.47
3 602.21 1192.79
4 605.93 1189.08
5 609.64 1185.82
6 613.41 1181.60
Calculate the total principal paid in the first six months.
MAP4C Lesson Assignment Page 3

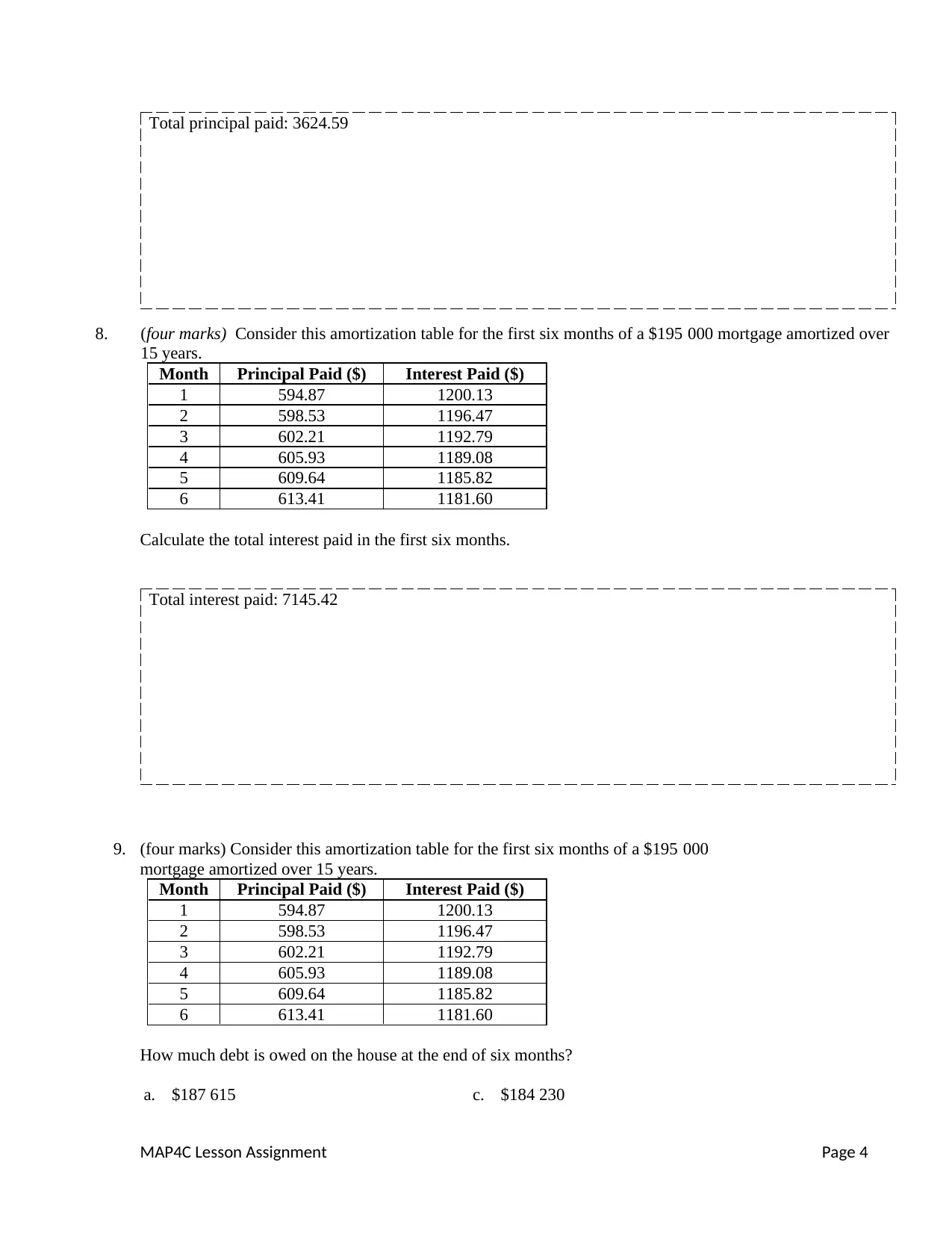
Total principal paid: 3624.59
8. (four marks) Consider this amortization table for the first six months of a $195 000 mortgage amortized over
15 years.
Month Principal Paid ($) Interest Paid ($)
1 594.87 1200.13
2 598.53 1196.47
3 602.21 1192.79
4 605.93 1189.08
5 609.64 1185.82
6 613.41 1181.60
Calculate the total interest paid in the first six months.
Total interest paid: 7145.42
9. (four marks) Consider this amortization table for the first six months of a $195 000
mortgage amortized over 15 years.
Month Principal Paid ($) Interest Paid ($)
1 594.87 1200.13
2 598.53 1196.47
3 602.21 1192.79
4 605.93 1189.08
5 609.64 1185.82
6 613.41 1181.60
How much debt is owed on the house at the end of six months?
a. $187 615 c. $184 230
MAP4C Lesson Assignment Page 4

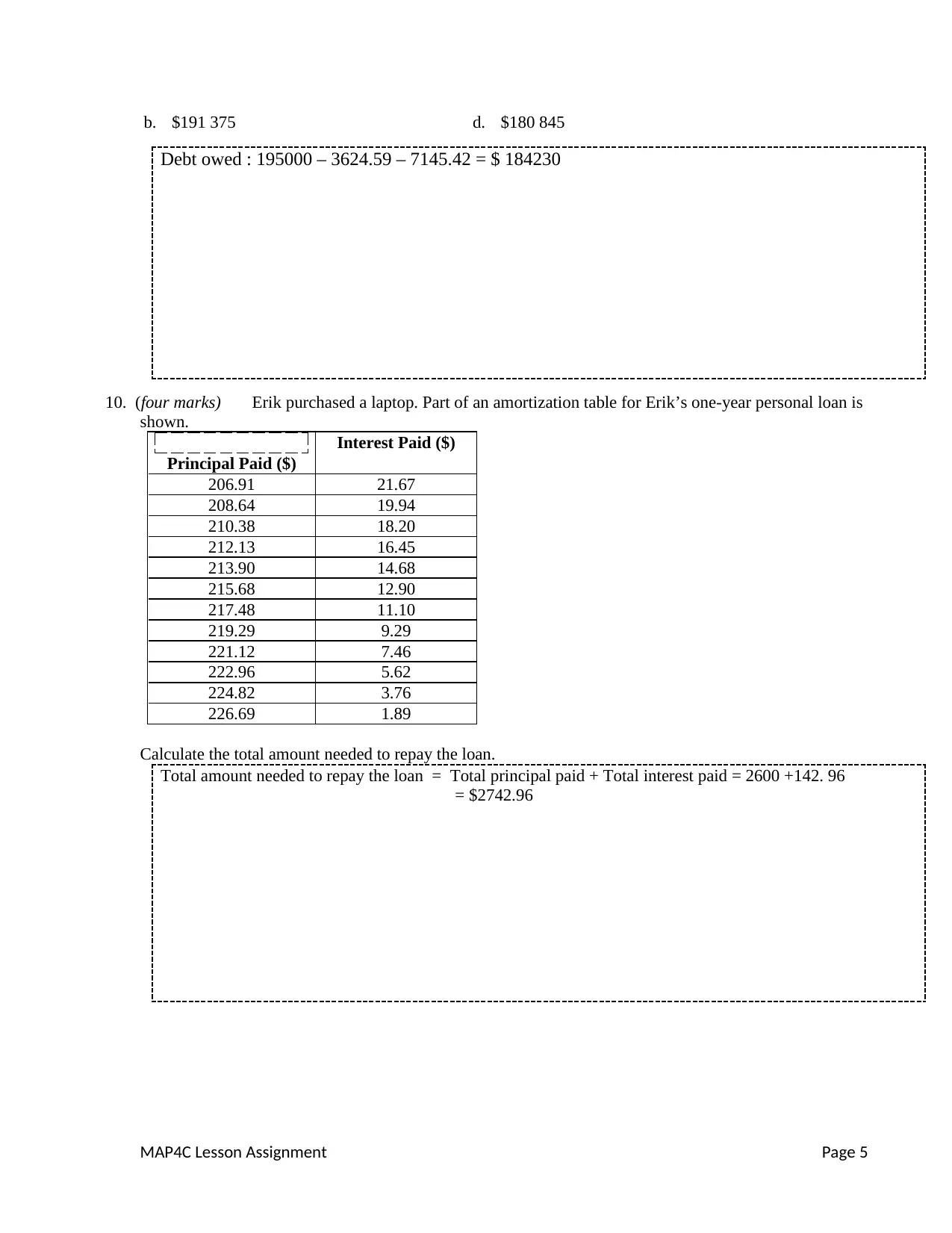
b. $191 375 d. $180 845
Debt owed : 195000 – 3624.59 – 7145.42 = $ 184230
10. (four marks) Erik purchased a laptop. Part of an amortization table for Erik’s one-year personal loan is
shown.
Principal Paid ($)
Interest Paid ($)
206.91 21.67
208.64 19.94
210.38 18.20
212.13 16.45
213.90 14.68
215.68 12.90
217.48 11.10
219.29 9.29
221.12 7.46
222.96 5.62
224.82 3.76
226.69 1.89
Calculate the total amount needed to repay the loan.
Total amount needed to repay the loan = Total principal paid + Total interest paid = 2600 +142. 96
= $2742.96
MAP4C Lesson Assignment Page 5

11. (four marks) Natalie recently purchased her first home for $166 000. Calculate the amount of Natalie’s
mortgage if she decided to make a 15% down payment and mortgage the rest.
Amount of Natalies mortgage : 166000 – 0.15*166000 = $141100
12. (four marks) Mikayla recently purchased her first home for $166 000. Mikayla decided to make a down
payment of $33 200 and mortgage the rest. She chose a five-year fixed rate mortgage amortized over 20 years
at 6.9% per year. Determine the amount still owing after five years.
Mortgaged amount : 166000 – 33200 = 132800
P = 132800 , r = 6.9% , n= 12, Y = 20
PMT = ( P∗r
n )/ [1−(1+ r
n )−nY
]
Solving,
PMT = 1021.64
Amount still owed = 132800 – 1021.64*12 = $120540.3
13. (four marks) Selena and Dustin have a pre-approved mortgage for $249 000. The current annual interest rate
for a five-year fixed rate mortgage is 6.19%. Determine the monthly payment for a 25-year amortization
period.
P = 249000, n = 12, r = 6.19 , Y =25
PMT = ( P∗r
n )/ [1−(1+ r
n )−nY
]
Solving we have,
Monthly payment : $1633.35
MAP4C Lesson Assignment Page 6

14. (four marks) Selena and Dustin have a pre-approved mortgage for $249 000. The current annual interest
rate for a five-year fixed rate mortgage is 6.19%. Determine the difference between the monthly payments for
a 15-year amortization period and a 20-year amortization period.
Monthly payment for 15 year amortization period: $2126.85
Monthly payment for 20 year amortization period: $1811.31
Difference: $2126.85 – $1811.31 = $315.54
15. (four marks) Curtis bought a condominium for $319 000 and made a down payment of $64 000. The annual
interest rate for a five-year fixed rate mortgage is 5.49%. Determine the monthly payment for a 25-year
amortization period.
Mortgaged amount : 319000-64000 = 255000
r = 5.49% , P = 255000, n = 12, Y = 25
PMT = $1564.40
16. (four marks) Curtis bought a condominium for $319 000 and made a down payment of $64 000. The annual
interest rate for a five-year fixed rate mortgage is 5.49%. Curtis has a choice between a 20-year amortization
period and a 25-year amortization period. How much less will Curtis pay by choosing the 20-year
amortization period?
Monthly payment for 25 year amortization period: $1564.40
Monthly payment for 20 year amortization period: $1752.67
Total savings if 20 year amortization period is chosen: 1564*25*12 - 1752.67*20*12
= $ 48559.2
MAP4C Lesson Assignment Page 7