MAT-121 College Algebra: Written Assignment 5 Solutions

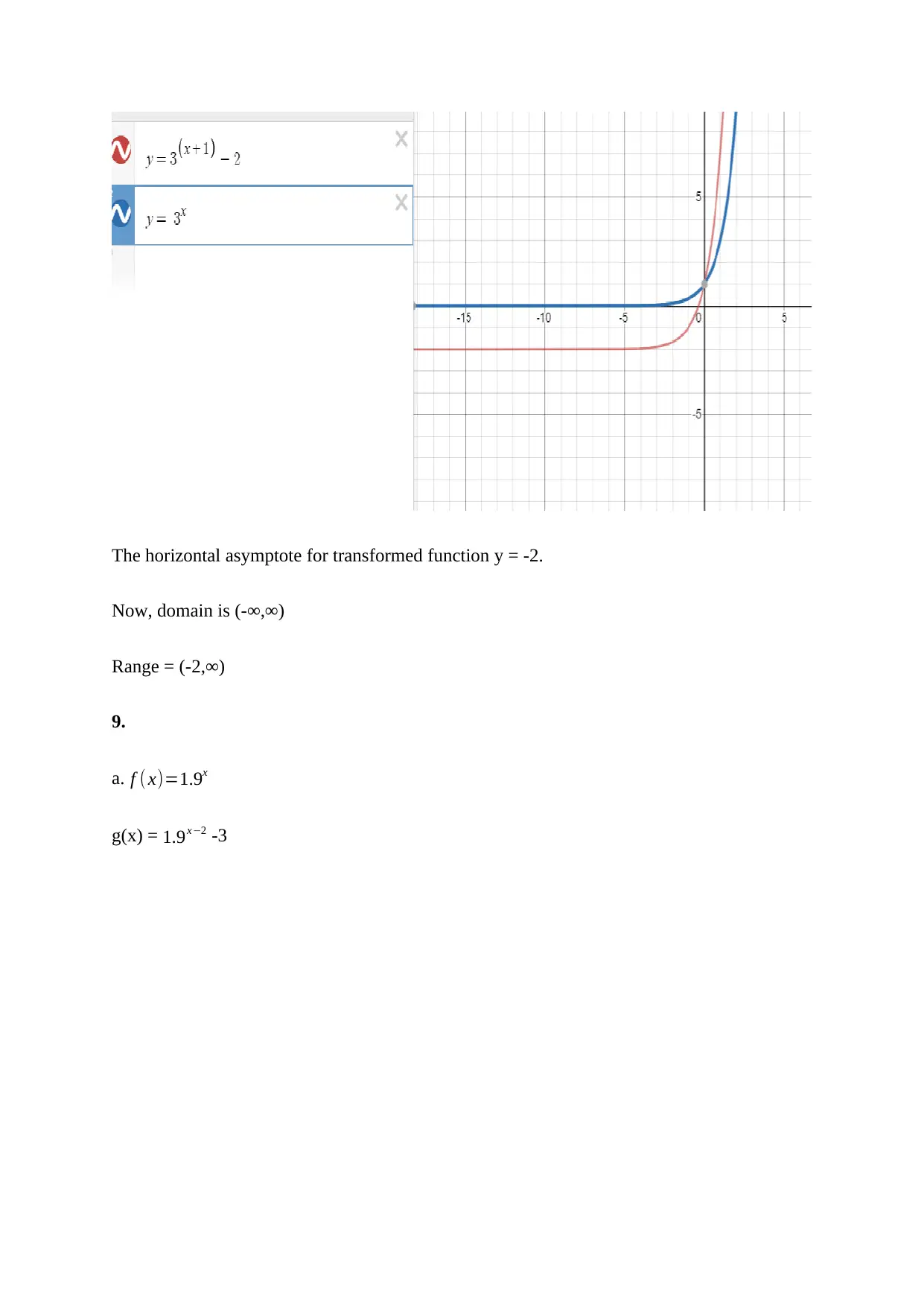
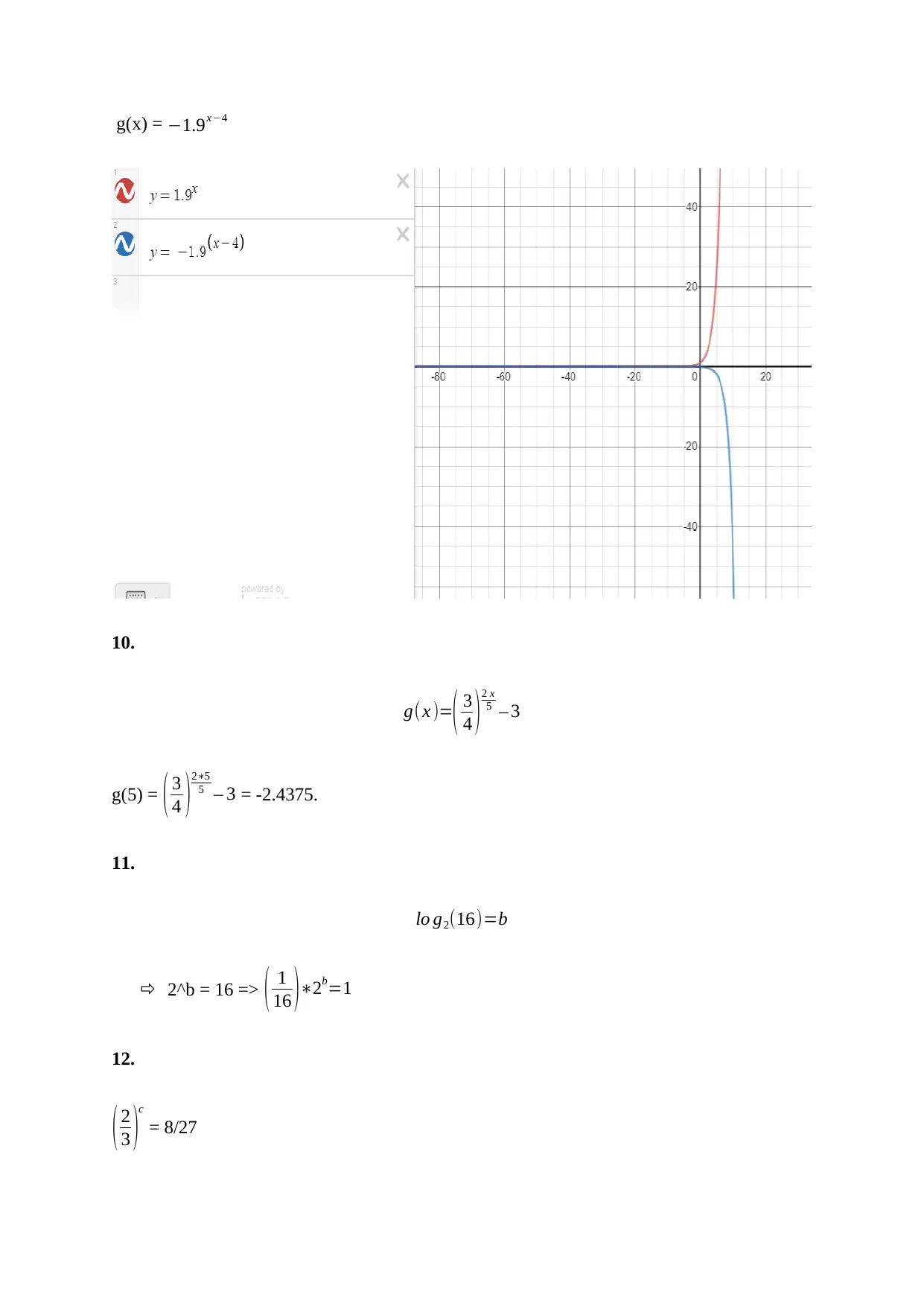
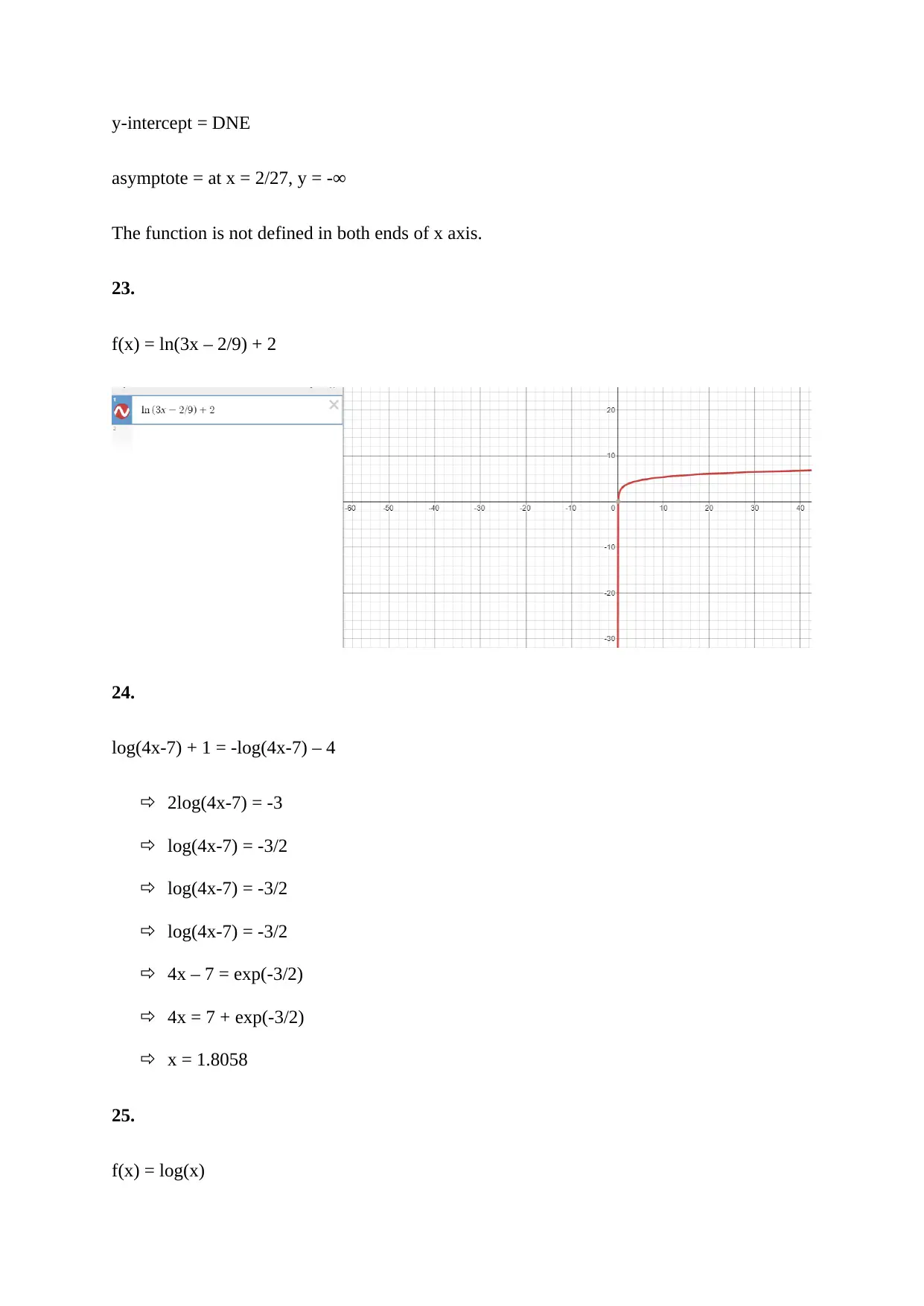
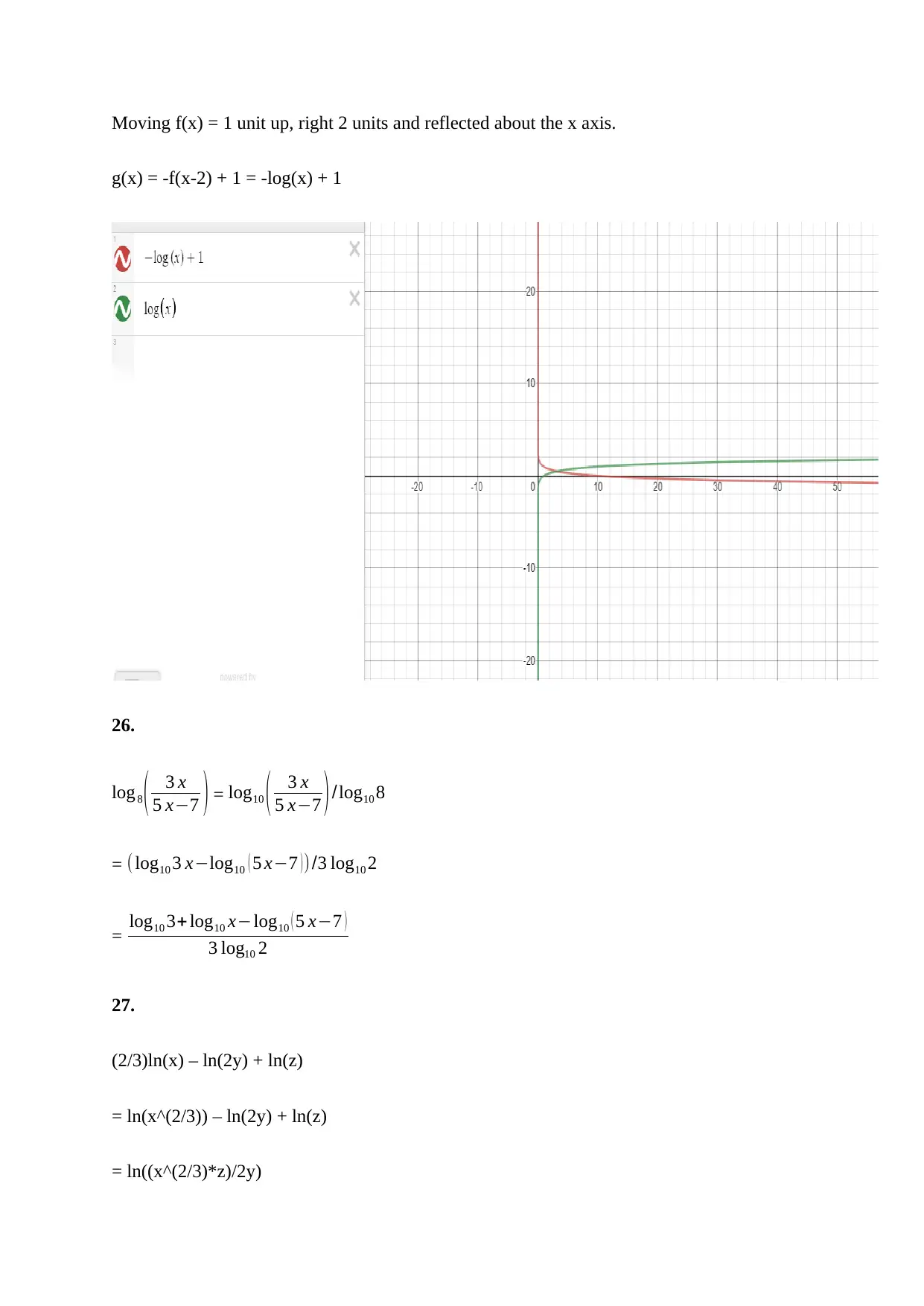
This document presents solutions to a college algebra assignment, addressing various concepts including exponential growth and decay, and finding exponential function formulas. The assignment includes problems on compound interest calculations, determining the initial deposit, and calculating the number of years for an investment. It also covers real-world applications like calculating the median house price appreciation over time. Further, the solutions include reflections about the y-axis, finding y-intercepts, and identifying horizontal asymptotes of transformed exponential functions. Logarithmic equations and their properties, including domain, range, intercepts, and asymptotes are also addressed. The assignment also includes solving logarithmic equations, exponential decay models, and half-life calculations, as well as applications of logarithms in earthquake magnitude comparisons and solving exponential equations. The document provides detailed step-by-step solutions to all the problems.

Running head: WRITTEN ASSIGNMENT 5
WRITTEN ASSIGNMENT 5
Name of the Student
Name of the University
Author Note

6.1:
1.
y=12.25 ( 2 x
3 )
3
When x increases 2x/3 decreases and its cube also decreases. Thus the function is
exponentially decaying.
2.
y= ( 7
8 )
0.75 x
−2
When x is positive then 0.75x is less than x and hence as x is increased in positive x axis then
the value asymptotically goes to zero. However, when x is increased in a negative direction
the value of y exponentially goes to infinity. Hence, the function exponentially increasing in
negative x and asymptotically goes to -2 in positive x direction.
3.
Let, the equation of the exponential function is
y = a*(b^x)
Now, function passes through (0,21) and (2,38)
Hence, 21 = a*b^0 => a = 21
And, 38 = a*b^2 => b^2 = 38/a => b = sqrt(38/21) = 1.345.
Hence, y=21∗(1.345x)
4.
(−1, 5) and (4, 2) points are in y = a*(b^x)

Hence, 5 = a*(b^-1) => 5 = a/b => a = 5b
And, 2 = a*(b^4) => 2 = 5b*b^4 => b^5 = 2/5 => b = 0.833.
a = 5*0.833 = 4.165
Hence, the exponential model = 4.165∗(0.833x )
5.
a. Given value of investment account = 15500 ( 1+ 0.06
6 ) 90
= 37953.806
b. The initial deposit made to the account is 15500.
c. The number of years taken for the account is 90/12 = 7.5 years.
6.
A( t)=P (1+ r
n )nt
P = value in 1980 = $95000
A(t) = $133300
n = 1, t = 20
133300 = 95000 ( 1+r ) 20
 ( 1+r ) 20=133300 / 95000
 20ln( 1+r ¿ = ln(133300/ 95000 ¿ = 0.3387
 ln(1+r) = 0.0169
 1+r = 1.017
 r = 0.017
 r = 1.7%

Now, if the same percentage continues then the median price in the year 2020 will be
A(40) = 95000 ( 1+0.017 ) 40 = $ 186449.71 ~ $ 186450
6.2:
7.
f(x) = (-2/3)(1.25)^(3x)
Reflection about y axis is f(-x) = (-2/3)(1.25)^(-3x)
Y intercept is (0,-0.667).
8.
Given f(x) = 3x+1 – 2

The horizontal asymptote for transformed function y = -2.
Now, domain is (-∞,∞)
Range = (-2,∞)
9.
a. f ( x)=1.9x
g(x) = 1.9x−2 -3

b. Shifting f(x) 2.25 units upward and left 1.5 units.
g(x) = 1.9x+1.5 +2.25
c. Shifting f(x) 4 units right and reflected about the x-axis.

g(x) = −1.9x−4
10.
g(x )=( 3
4 ) 2 x
5 – 3
g(5) = ( 3
4 )2∗5
5 – 3 = -2.4375.
11.
lo g2(16)=b
 2^b = 16 => ( 1
16 )∗2b=1
12.
( 2
3 )
c
= 8/27

 c*ln(2/3) = ln(8/27) => c*ln(2/3) = 3ln(2/3)
13.
lo g16 ( x )=3
 x = 16^3 = 4096
14.
4*log(1000) = 4log(10^3) = 4*3log(10) = 4*3 = 12.
15.
lo g16( 0.0625) = lo g16 ( 1
2 )4
= 4∗lo g16 (1/2) = −4∗lo g16 (2) = -4/lo g2(16)
= −4
4 lo g2 2 = -1
16.
log(0.01) = -2log(10) = -2.
17.
ln(exp(-4)) -2 = -4 – 2= -6
18.
log(0.2345) = -0.629857 = -0.630
19.
log(10)/(log(10^3.45)) = log(10)/(3.45log(10)) = 1/3.45 (proved)
20.
M1 = magnitude of OK earthquake.

M2 = magnitude of Papua New Guinea earthquake.
log(I1/I2) = M1 – M2
 log(I1/I2) = 4.6 – 6.3
 log(I1/I2) = -1.7
 I1/I2 = exp(-1.7) = 0.183
 I2/I1 = 5.464
Hence, the intensity of Papua New Guinea is 5.464 time greater than the intensity of POK.
21.
f(x) = 2 lo g8 (4−x)
Domain = (-∞,4)
Range = (-∞,∞)
x-intercept = (3,0)
y-intercept = (0,1.333)
asymptote = at x = 4 y = -∞
The function is not defined in both ends of x axis.
22.
f(x) = ln(3x – 2/9) + 2
Domain = (2/27,∞)
Range = (-∞,∞)
x-intercept = (0.119,0)

y-intercept = DNE
asymptote = at x = 2/27, y = -∞
The function is not defined in both ends of x axis.
23.
f(x) = ln(3x – 2/9) + 2
24.
log(4x-7) + 1 = -log(4x-7) – 4
 2log(4x-7) = -3
 log(4x-7) = -3/2
 log(4x-7) = -3/2
 log(4x-7) = -3/2
 4x – 7 = exp(-3/2)
 4x = 7 + exp(-3/2)
 x = 1.8058
25.
f(x) = log(x)

Moving f(x) = 1 unit up, right 2 units and reflected about the x axis.
g(x) = -f(x-2) + 1 = -log(x) + 1
26.
log8 ( 3 x
5 x−7 ) = log10 ( 3 x
5 x−7 )/log10 8
= ( log10 3 x−log10 ( 5 x−7 )) /3 log10 2
= log10 3+ log10 x−log10 ( 5 x−7 )
3 log10 2
27.
(2/3)ln(x) – ln(2y) + ln(z)
= ln(x^(2/3)) – ln(2y) + ln(z)
= ln((x^(2/3)*z)/2y)

28.
ln ( x3∗4
√ y3
( 2 z ) 4 ) = ln ( x3 ) + ( 3
4 )∗ln ( y ) −4 ln (2 z)
= 3 ln ( x )+ ( 3
4 )∗ln ( y )−4 ln ( 2 )−4 ln ( z )
29.
lo g8 (24) = lo g10 24
log10 8 = lo g10 3+ 3 log10 2
3 log10 2
30.
lo g3( 7) = m and lo g3 ( 5 ) =n
Hence, lo g7 (25) = lo g7 (52) = lo g3( 52)/lo g3 (7) = 2(lo g3 ( 5 ) )/lo g3 (7)= 2n
m
31.
log13 68 = log10 68
log10 13 = 2 log10 2+log10 17
log10 13 = 1.64506.
32.
log3 ( 3 x−5 ) +log3 ( 2 x+ 4 )=3
 ( 3 x−5 ) ( 2 x + 4 ) =27
 6x^2 +12x -10x -20 = 27
 6x^2 +2x – 47 = 0
 x = -2.97 and 2.637
33.

73 x – 1=74 x+5
 log10 73 x−1=log10 74 x +5
 3x-1 = 4x + 5
 x = -6
34.
57 x+1=84 x +5
 log10 57 x +1=log10 84 x+5
 (7x+1)/(4x+5) = lo g10 8
log10 5
 (7x+1)/(4x+5) = 1.292
 7x + 1= 5.168x + 6.46
 1.832x = 5.46
 x = 2.98
35.
6 lo g9 (3 a)=15
 lo g9 ( 3 a ) =15/ 6
 lo g9 3+log3 a=15 /6
 log3 a=15
6 −1
2 =2
 a = 9.
36.
log(7x + 3) = log(5/(2x+3))
 7x + 3= 5/(2x+3)

 (7x + 3)(2x+3) = 5
 14x^2 + 27x + 9 = 5
 14x^2 + 27x + 4 = 0
 x = (-27-√505)/28 and (-27+√505)/28
37.
ln (x − 5) = ln (x − 7) + ln (2x − 1)
 ln (x − 5) = ln((x-7)(2x-1))
 x- 5 = (x-7)(2x-1)
 x-5 = 2x^2 -15x + 7
 2x^2 -16x + 12 = 0
 x^2 -8x + 6 = 0
 x = 4-√10 and 4+√10
38.
P = $10500
r = 4.25% annually = 0.0425
Now, final amount = 2P
A(t) = P*exp(r*t)
2P= P*exp(0.0425t)
 exp(0.0425t) = 2
 0.0425t = ln(2)
 t = 16.309 years.
39.

P0 = 165 mg.
r = 36% each hour.
Hence, P(t) = P0exp(at) = 165exp(at) ( t in hours)
P(1) = 165exp(a) (after 1 hour
 165*0.64 = 165exp(a)
 exp(a) = 0.64
 a = ln(0.64) = -0.446
Hence, the exponential decay model is P(t) = 165exp(-0.446t)
Now, half-life is calculated from the following equation.
165/2 = 165exp(-0.446t)
 exp(-0.446t) = ½
 -0.446t = ln(1/2)
 -0.446t = -0.693
 t = 1.554 hours.
Hence, half life therapeutic drug is 1.554 hours.
40.
t 1
2 of plutonium 238 = 87.75 years
Let, initial population is P0
Hence, P0/2 = P0*exp(a*87.75)
 exp(a*87.75) = 0.5
 a*87.75 = -0.693

 a = -0.0079
Hence, decay rate is 0.0079 per year or 0.79% per year.