Montgomery County Community College MAT 142 Exam 2 Solution

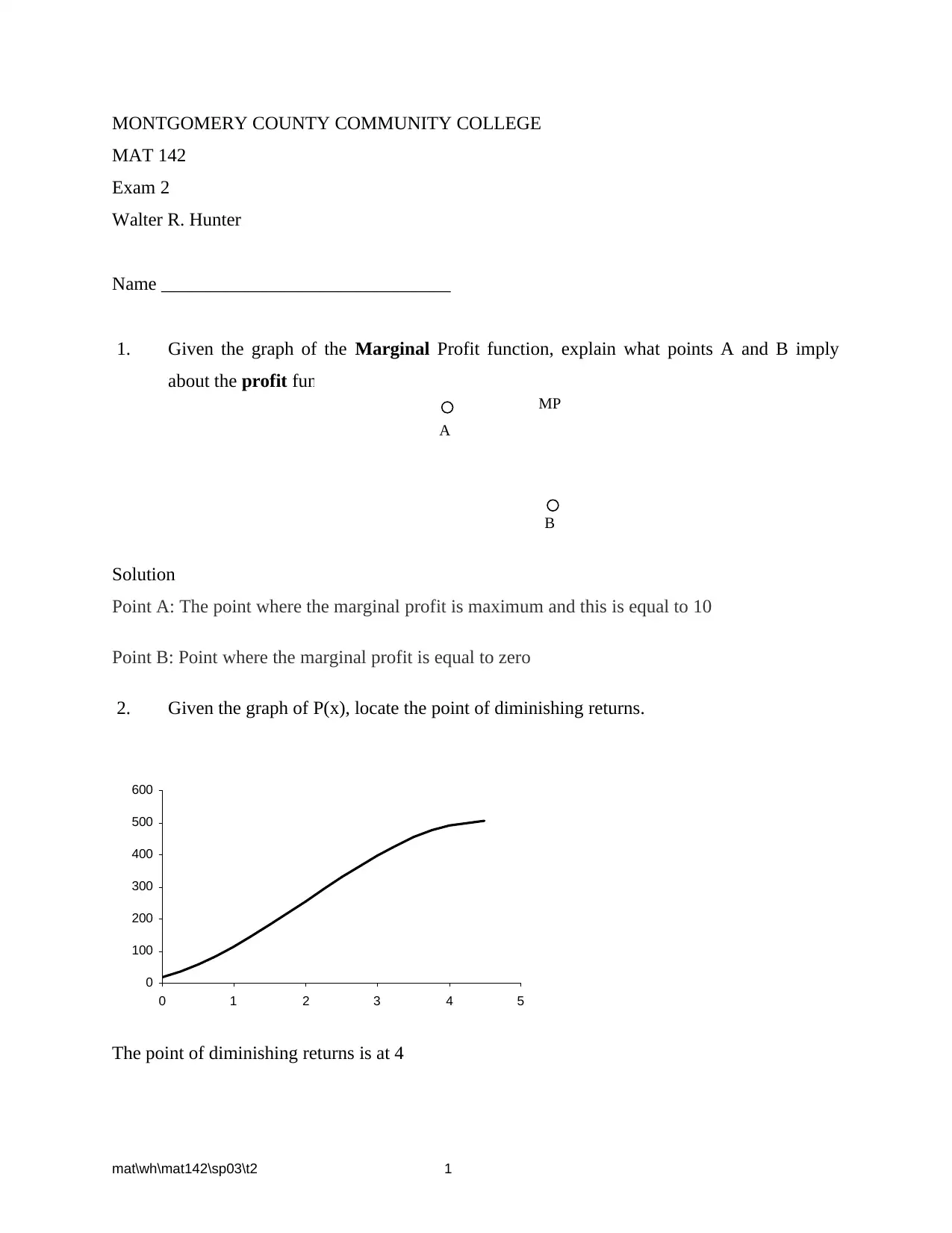
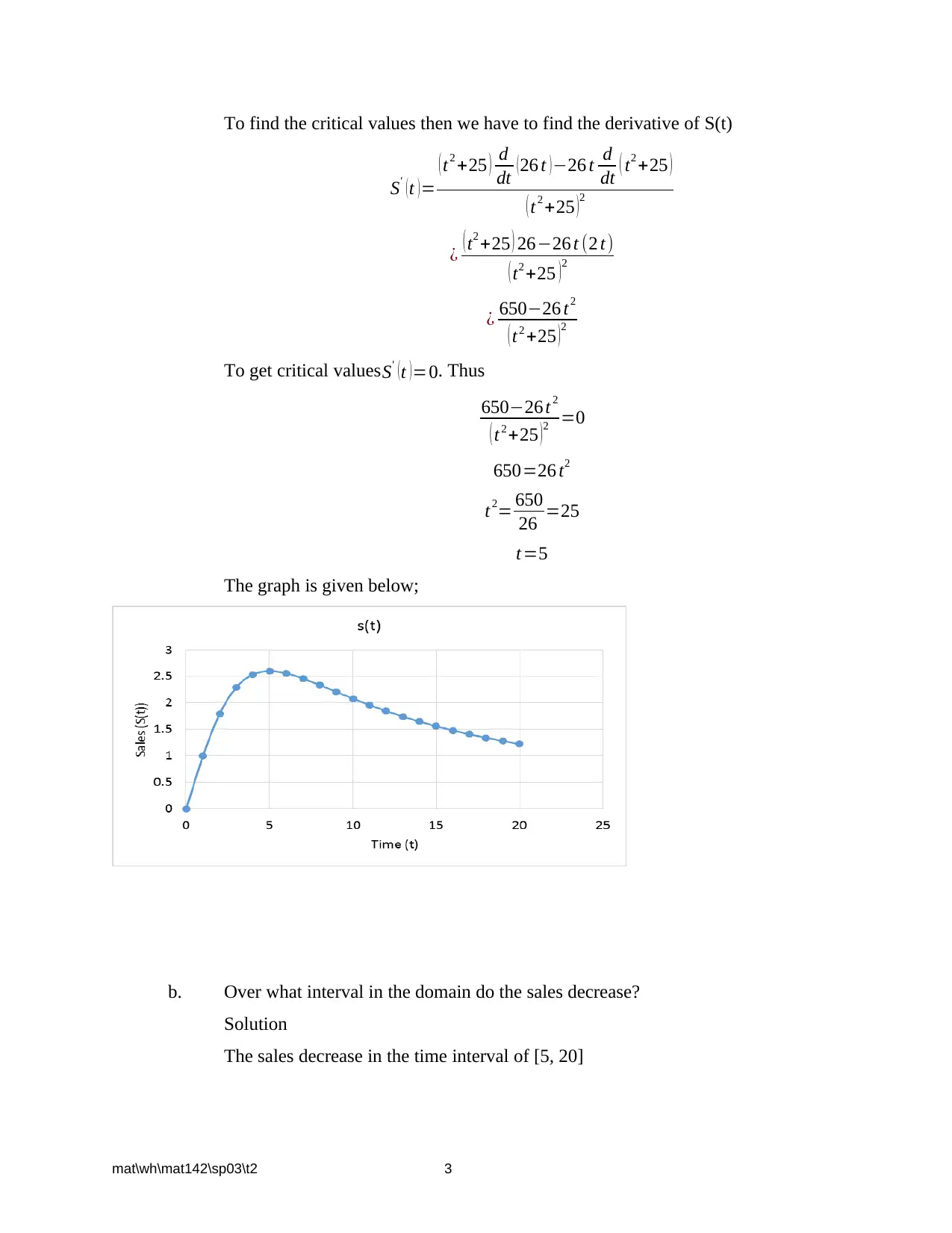
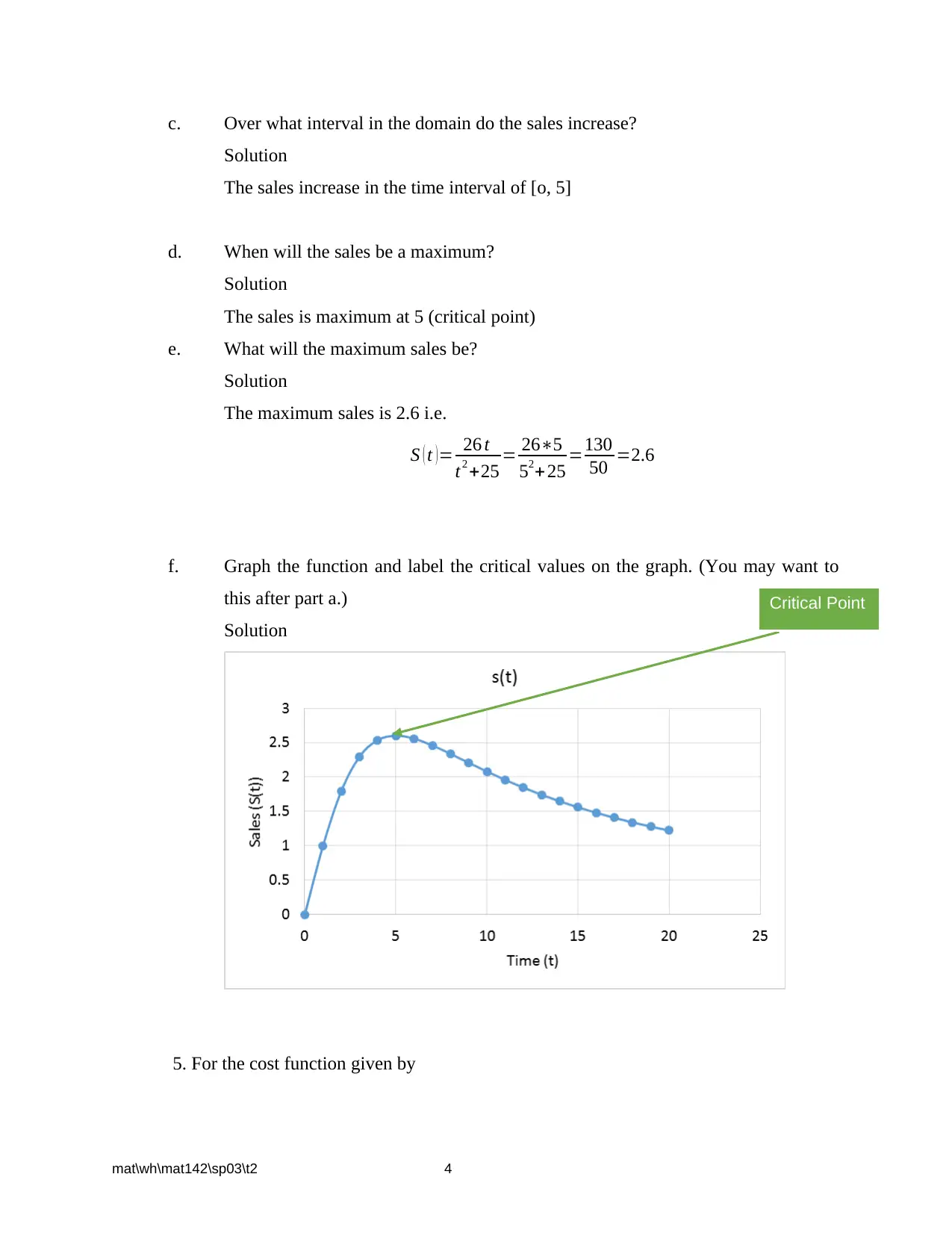
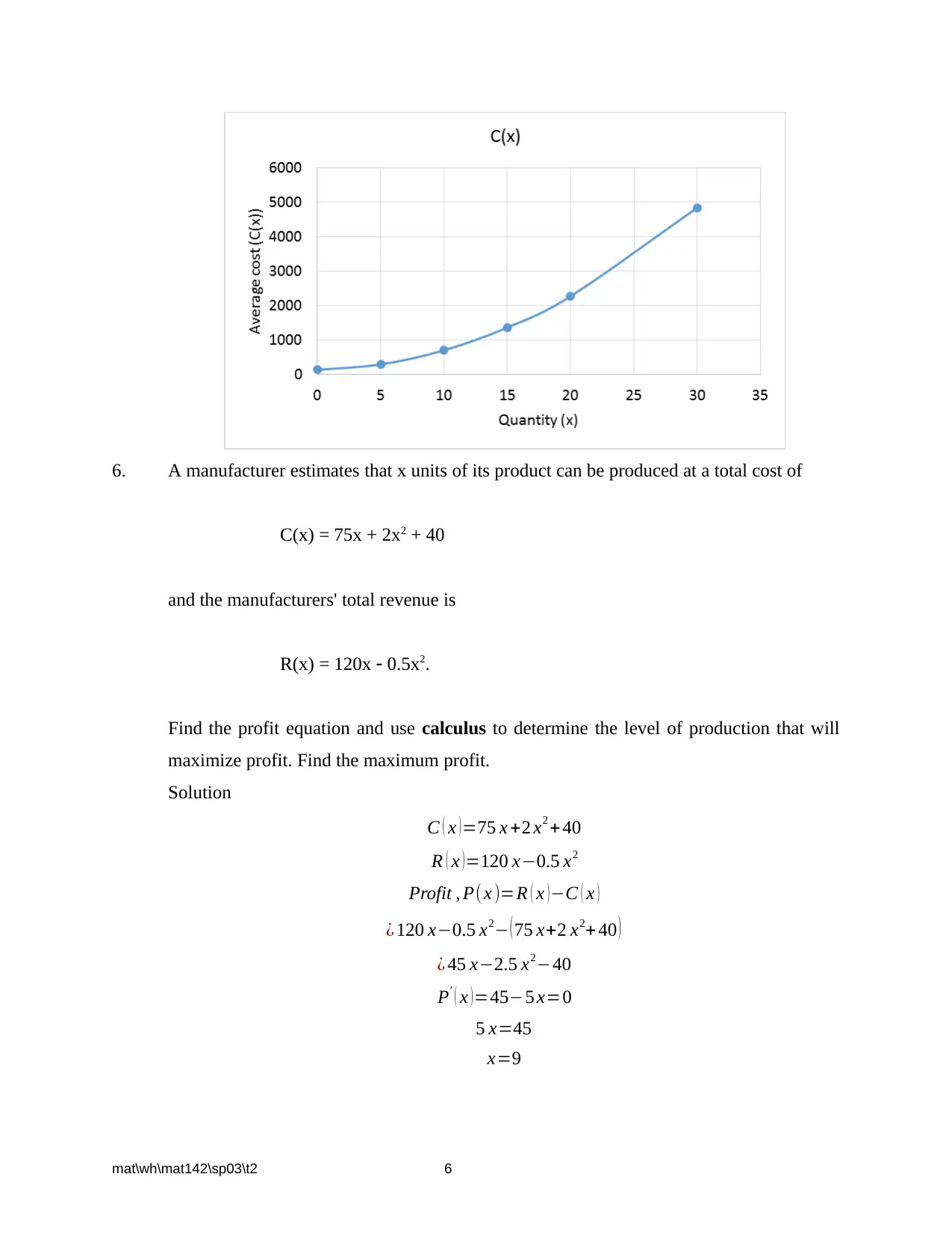
This document presents a comprehensive solution set for the MAT 142 Exam 2, covering a range of calculus concepts and problem types. The solutions address questions related to marginal profit analysis, identifying points of diminishing returns from graphs and equations, and determining the implications of these points. The assignment includes problems involving cost and revenue functions, requiring the calculation of critical values, intervals of increase and decrease, and the maximization of sales and profit. Furthermore, the solutions demonstrate the application of calculus to optimize production and minimize costs, including problems related to production runs and inventory management. Detailed step-by-step solutions are provided for each problem, including graphical representations where applicable, ensuring a thorough understanding of the concepts and problem-solving techniques. This resource is designed to help students grasp the core principles of calculus and prepare for similar exams.

MONTGOMERY COUNTY COMMUNITY COLLEGE
MAT 142
Exam 2
Walter R. Hunter
Name _______________________________
1. Given the graph of the Marginal Profit function, explain what points A and B imply
about the profit function.
Solution
Point A: The point where the marginal profit is maximum and this is equal to 10
Point B: Point where the marginal profit is equal to zero
2. Given the graph of P(x), locate the point of diminishing returns.
0
100
200
300
400
500
600
0 1 2 3 4 5
The point of diminishing returns is at 4
mat\wh\mat142\sp03\t2 1
A
B
MP

3. Suppose that the total number of units produced by a worker in t hours of an 8 hour day
can be modeled by
P(t) = 25t + 6t2  t3
Find the point of diminishing returns. Explain what this point means in terms of units
produced by a worker.
Solution
P(t)=25 t+6 t2 t3
dP
dt =25+12 t−3 t2
Solving25+12 t−3 t2 yields
t=5.51∧−1.51
But we can’t have negative time. Next we check whether it is a
minimum or a maximum
d2 P
d t 2 =12−6 t <0 , t=5.51 ismaximum
Thus Diminished return
t=5.51
Maximum units = 25 ( 5.51 ) +6 ( 5.51 )2 ( 5.51 )3=152.63 ≈ 153
This point means that for maximum units to be produced a worker has to work for 5.51 hours
and the maximum units at this time is 153 units.
4. The weekly sales S of a product during an advertising campaign are given by
, 0  t  20
a. Use calculus to find the critical values that lie in the domain of the problem.
Solution
mat\wh\mat142\sp03\t2 2

To find the critical values then we have to find the derivative of S(t)
S' ( t ) =
( t2 +25 ) d
dt ( 26 t ) −26 t d
dt ( t2 +25 )
( t2 +25 ) 2
¿ ( t2 +25 ) 26−26 t (2 t)
( t2 +25 )
2
¿ 650−26 t2
( t2 +25 ) 2
To get critical values S' ( t ) =0. Thus
650−26 t 2
( t2 +25 )2 =0
650=26 t2
t2= 650
26 =25
t=5
The graph is given below;
b. Over what interval in the domain do the sales decrease?
Solution
The sales decrease in the time interval of [5, 20]
mat\wh\mat142\sp03\t2 3

c. Over what interval in the domain do the sales increase?
Solution
The sales increase in the time interval of [o, 5]
d. When will the sales be a maximum?
Solution
The sales is maximum at 5 (critical point)
e. What will the maximum sales be?
Solution
The maximum sales is 2.6 i.e.
S ( t )= 26 t
t2 +25 = 26∗5
52+ 25 =130
50 =2.6
f. Graph the function and label the critical values on the graph. (You may want to
this after part a.)
Solution
5. For the cost function given by
mat\wh\mat142\sp03\t2 4
Critical Point

C(x) = 5x2 + 7x + 125
a. Find the average cost function.
Solution
Average ost function ,C ( x)=C ( x )
x = 5 x2 +7 x +125
x
b. Use calculus to find the minimum of the average cost function.
Solution
C ( x)= C ( x )
x = 5 x2 +7 x+125
x
C ( x ) =5 x +7+ 125
x
C' ( x )=5−125
x2
Finding the critical point C' ( x )=0
5−125
x2 =0
5=125
x2
x2= 125
5 =25
x=± 5
-5 is invalid critical point since quantity can’t be negative.
Second derivative C'' ( x ) >0thus x gives minimum C (x)
Minimum average cost is thus;
C ( 5 ) =5 ( 5 )2 +7 ( 5 ) +125
5 = 285
5 =57
c. Graph the average cost function.
Solution
mat\wh\mat142\sp03\t2 5

6. A manufacturer estimates that x units of its product can be produced at a total cost of
C(x) = 75x + 2x2 + 40
and the manufacturers' total revenue is
R(x) = 120x  0.5x2.
Find the profit equation and use calculus to determine the level of production that will
maximize profit. Find the maximum profit.
Solution
C ( x )=75 x +2 x2 + 40
R ( x ) =120 x−0.5 x2
Profit , P( x )=R ( x ) −C ( x )
¿ 120 x−0.5 x2− ( 75 x+2 x2+ 40 )
¿ 45 x−2.5 x2−40
P' ( x )=45−5 x=0
5 x=45
x=9
mat\wh\mat142\sp03\t2 6

P' ' ( x )=−5< 0; P ( x ) is maximum
Profit is maximum when x =9
Max profit: 45 ( 9 ) −2.5 ( 9 ) 2 −40=162.5
7. A company needs 150,000 items per year. Production costs are $360 to prepare for a
production run and $7 for each item produced. Inventory costs are $0.75 per item per
year. Find the number of items that should be produced in each run so that the total costs
of production and storage are minimized. You must use calculus.
Solution
So if x is the number of production runs, then 150000
x is the number of items produced in a
production run. Since every production run costs 360 then that part of the cost is 360x. And
presumably we will at some point store every one of these units per production run, at a cost of
(0.75)490000/x. So the total cost function is
C ( x )=360 x + (0.75)1500000
x
And you want to minimize this, so you take the derivative and set it to 0, then solve for x:
C' ( x ) =360+112500 ( −1
x2 ) =0
112500
x2 =360
x2= 112500
360
So x=17.7 (rejecting the negative solution as meaningless in the problem)
Since we need to know the number of items produced in each run so we will test it for 17 and 18
both as the value of x is not an integral value.
Substituting x = 17, total cost (y) = 360*17 + 112,500/17 ≈ $12,737.65
Substituting x = 18, total cost (y) = 360*18 + 112,500/18 = $12,730
mat\wh\mat142\sp03\t2 7

Clearly, it is visible that the cost is a little lesser when x = 18 so the number of items in each run
for minimum cost is 150,000/18 ≈8333
mat\wh\mat142\sp03\t2 8