Statistical Analysis Project Part B: MAT10251, SCU - Internet Speed

This project analyzes internet speed data using statistical methods. It begins with calculating a confidence interval for the proportion of time download speeds are at least 80% of the maximum. A one-sample t-test is then used to test the company's claim about average evening download speeds. Precision of the download speed tests is assessed using an independent sample t-test. Simple linear regression is applied to explore the relationship between upload and download speeds. Finally, multiple linear regression evaluates the impact of download speed and evening time on upload speed. The project includes the use of Excel for calculations and interpretation of results.

SOUTHERN CROSS UNIVERSITY
School of Business and Tourism
MAT10251 Statistical Analysis
PROJECT COVER SHEET
Please complete all of the following details and then make these sheets the first pages of
your project – do not send it as a separate document.
Your project must be submitted as a Word document.
PART B
Student Name:
Student ID No.:
Tutor’s name:
Due date:
Date submitted:
Declaration:
I have read and understand the Rules Relating to Awards (Rule 3 Section 18 –
Academic Integrity) as contained in the SCU Policy Library. I understand the
penalties that apply for academic misconduct and agree to be bound by these
rules.
The work I am submitting electronically is entirely my own work.
Signed:
(please type
your name)
Date:

STUDENT NAME:
STUDENT ID NUMBER:
MAT10251 – Statistical Analysis
Project Part B
Sample Number (last digit of your student ID number) 5
Confidence Level 95%
Level of Significance 5
Value: 25%
2

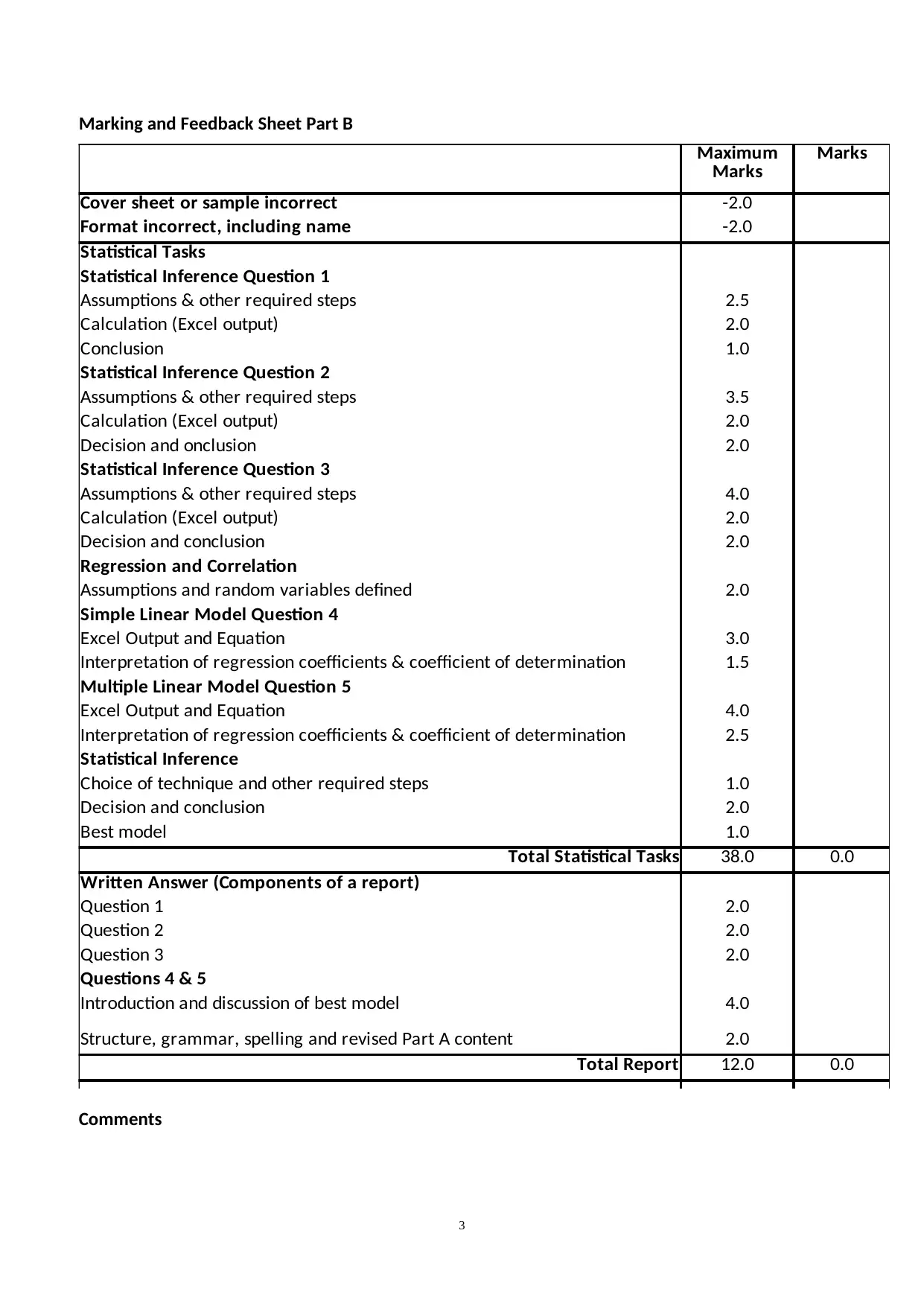
Marking and Feedback Sheet Part B
Marks
Cover sheet or sample incorrect -2.0
Format incorrect, including name -2.0
Statistical Tasks
Statistical Inference Question 1
Assumptions & other required steps 2.5
Calculation (Excel output) 2.0
Conclusion 1.0
Statistical Inference Question 2
Assumptions & other required steps 3.5
Calculation (Excel output) 2.0
Decision and onclusion 2.0
Statistical Inference Question 3
Assumptions & other required steps 4.0
Calculation (Excel output) 2.0
Decision and conclusion 2.0
Regression and Correlation
Assumptions and random variables defined 2.0
Simple Linear Model Question 4
Excel Output and Equation 3.0
Interpretation of regression coefficients & coefficient of determination 1.5
Multiple Linear Model Question 5
Excel Output and Equation 4.0
Interpretation of regression coefficients & coefficient of determination 2.5
Statistical Inference
Choice of technique and other required steps 1.0
Decision and conclusion 2.0
Best model 1.0
Total Statistical Tasks 38.0 0.0
Written Answer (Components of a report)
Question 1 2.0
Question 2 2.0
Question 3 2.0
Questions 4 & 5
Introduction and discussion of best model 4.0
Structure, grammar, spelling and revised Part A content 2.0
Total Report 12.0 0.0
Maximum
Marks
Comments
3

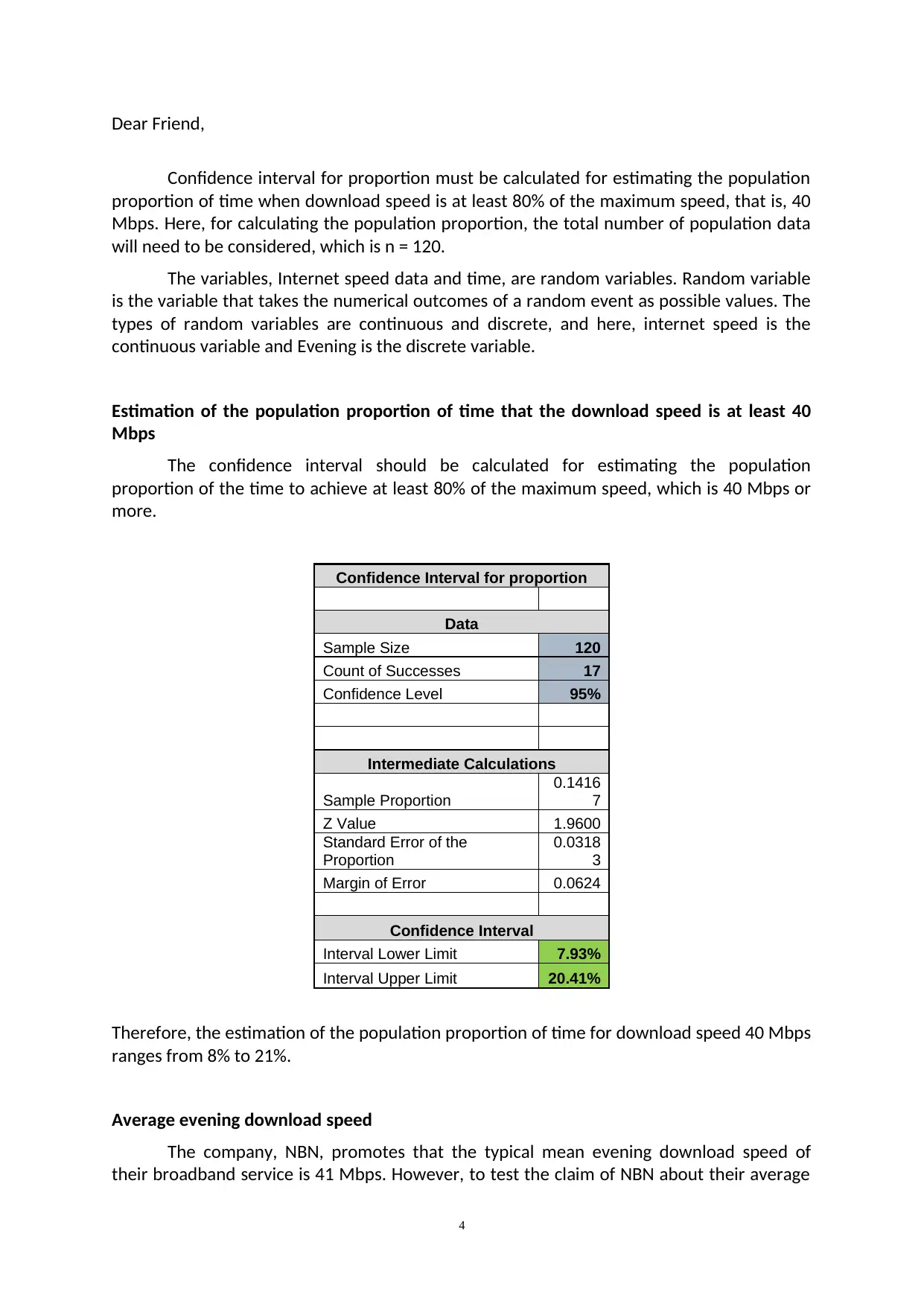
Dear Friend,
Confidence interval for proportion must be calculated for estimating the population
proportion of time when download speed is at least 80% of the maximum speed, that is, 40
Mbps. Here, for calculating the population proportion, the total number of population data
will need to be considered, which is n = 120.
The variables, Internet speed data and time, are random variables. Random variable
is the variable that takes the numerical outcomes of a random event as possible values. The
types of random variables are continuous and discrete, and here, internet speed is the
continuous variable and Evening is the discrete variable.
Estimation of the population proportion of time that the download speed is at least 40
Mbps
The confidence interval should be calculated for estimating the population
proportion of the time to achieve at least 80% of the maximum speed, which is 40 Mbps or
more.
Confidence Interval for proportion
Data
Sample Size 120
Count of Successes 17
Confidence Level 95%
Intermediate Calculations
Sample Proportion
0.1416
7
Z Value 1.9600
Standard Error of the
Proportion
0.0318
3
Margin of Error 0.0624
Confidence Interval
Interval Lower Limit 7.93%
Interval Upper Limit 20.41%
Therefore, the estimation of the population proportion of time for download speed 40 Mbps
ranges from 8% to 21%.
Average evening download speed
The company, NBN, promotes that the typical mean evening download speed of
their broadband service is 41 Mbps. However, to test the claim of NBN about their average
4

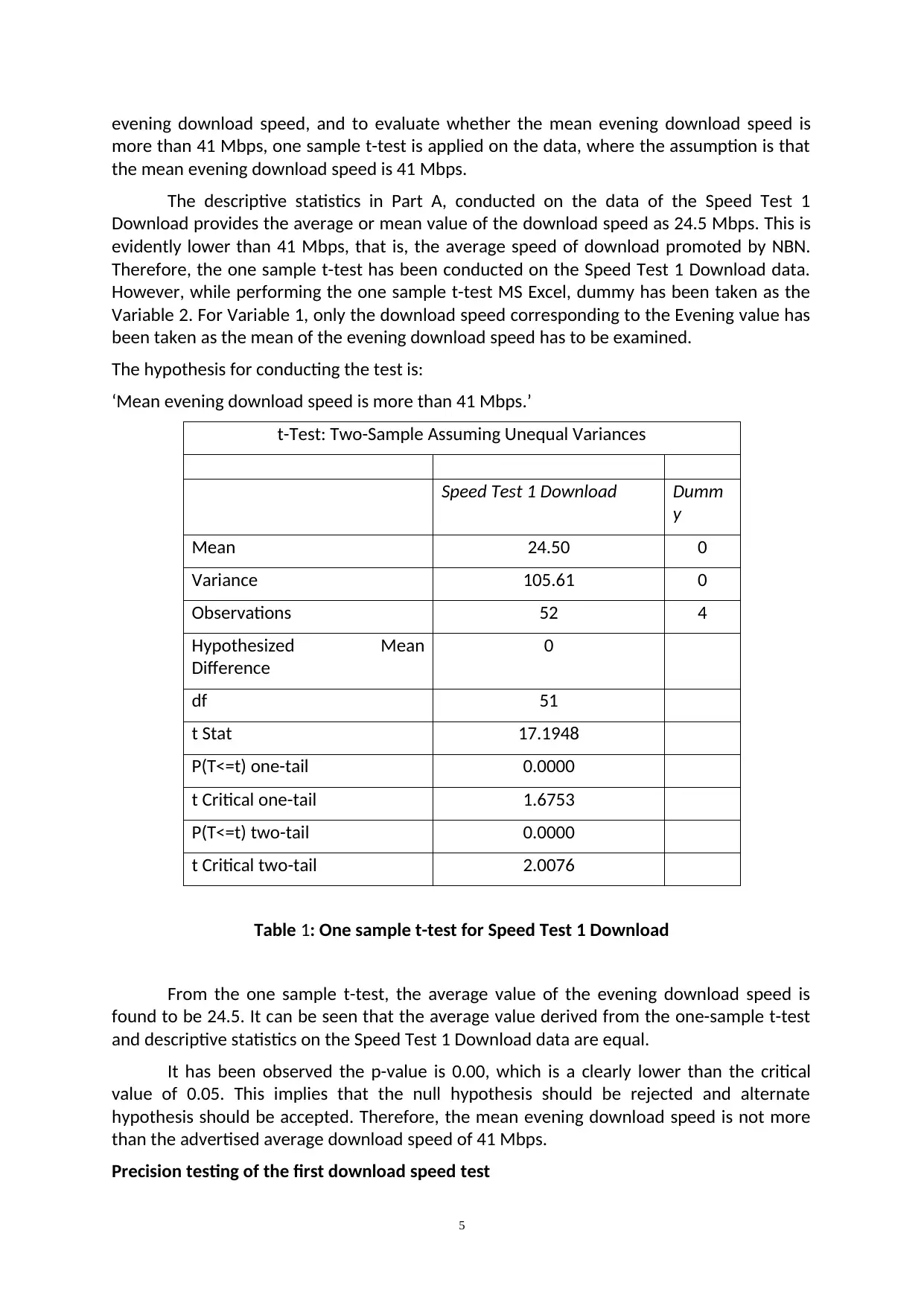
evening download speed, and to evaluate whether the mean evening download speed is
more than 41 Mbps, one sample t-test is applied on the data, where the assumption is that
the mean evening download speed is 41 Mbps.
The descriptive statistics in Part A, conducted on the data of the Speed Test 1
Download provides the average or mean value of the download speed as 24.5 Mbps. This is
evidently lower than 41 Mbps, that is, the average speed of download promoted by NBN.
Therefore, the one sample t-test has been conducted on the Speed Test 1 Download data.
However, while performing the one sample t-test MS Excel, dummy has been taken as the
Variable 2. For Variable 1, only the download speed corresponding to the Evening value has
been taken as the mean of the evening download speed has to be examined.
The hypothesis for conducting the test is:
‘Mean evening download speed is more than 41 Mbps.’
t-Test: Two-Sample Assuming Unequal Variances
Speed Test 1 Download Dumm
y
Mean 24.50 0
Variance 105.61 0
Observations 52 4
Hypothesized Mean
Difference
0
df 51
t Stat 17.1948
P(T<=t) one-tail 0.0000
t Critical one-tail 1.6753
P(T<=t) two-tail 0.0000
t Critical two-tail 2.0076
Table 1: One sample t-test for Speed Test 1 Download
From the one sample t-test, the average value of the evening download speed is
found to be 24.5. It can be seen that the average value derived from the one-sample t-test
and descriptive statistics on the Speed Test 1 Download data are equal.
It has been observed the p-value is 0.00, which is a clearly lower than the critical
value of 0.05. This implies that the null hypothesis should be rejected and alternate
hypothesis should be accepted. Therefore, the mean evening download speed is not more
than the advertised average download speed of 41 Mbps.
Precision testing of the first download speed test
5

A second download speed test, that is, Speed Test 2 was performed for examining
the accuracy of the Speed Test 1 Download data. It was assumed that both speed tests, that
is, Speed Test 1 Download and Speed Test 2 Download would produce the same download
speed. To check the precision of the Speed Test 1 Download data, independent sample t-
test has been performed on the data of Speed Test 1 Download and Speed Test 2 Download.
Therefore, the hypothesis to be examined is:
‘There is no difference in the average download speed generated by the two speed tests’
t-Test: Two-Sample Assuming Unequal Variances
Speed Test 1
Download
Speed Test 2 Download
Mean 26.73 29.64
Variance 97.58 90.09
Observations 120 120
Hypothesized Mean
Difference
0
df 238
t Stat -2.3250
P(T<=t) one-tail 0.0105
t Critical one-tail 1.6513
P(T<=t) two-tail 0.0209
t Critical two-tail 1.9700
Table 2: Independent sample t-test for Speed Test 1 Download and Speed Test 2
Download
The independent sample t-test generates the mean or average value for Speed Test
1 Download as 26.73 and Speed Test 2 Download as 29.64. The value of t-stat, that is, -
2.325, is lower than the –t critical two-tail, that is, -1.97 (at 95% confidence interval and 5%
level of significance), and therefore, the null hypothesis must be rejected. Hence, it is
proved that there is difference between the average download speeds generated by the two
speed tests.
Relationship between the upload and download speed
For exploring the association between the Speed Test 1 Download (independent or
predictor variable) and Speed Test 1 Upload data (dependent or response variable) and for
finding out the effect of the download speed on the upload speed, Simple Linear regression
model is applied.
6

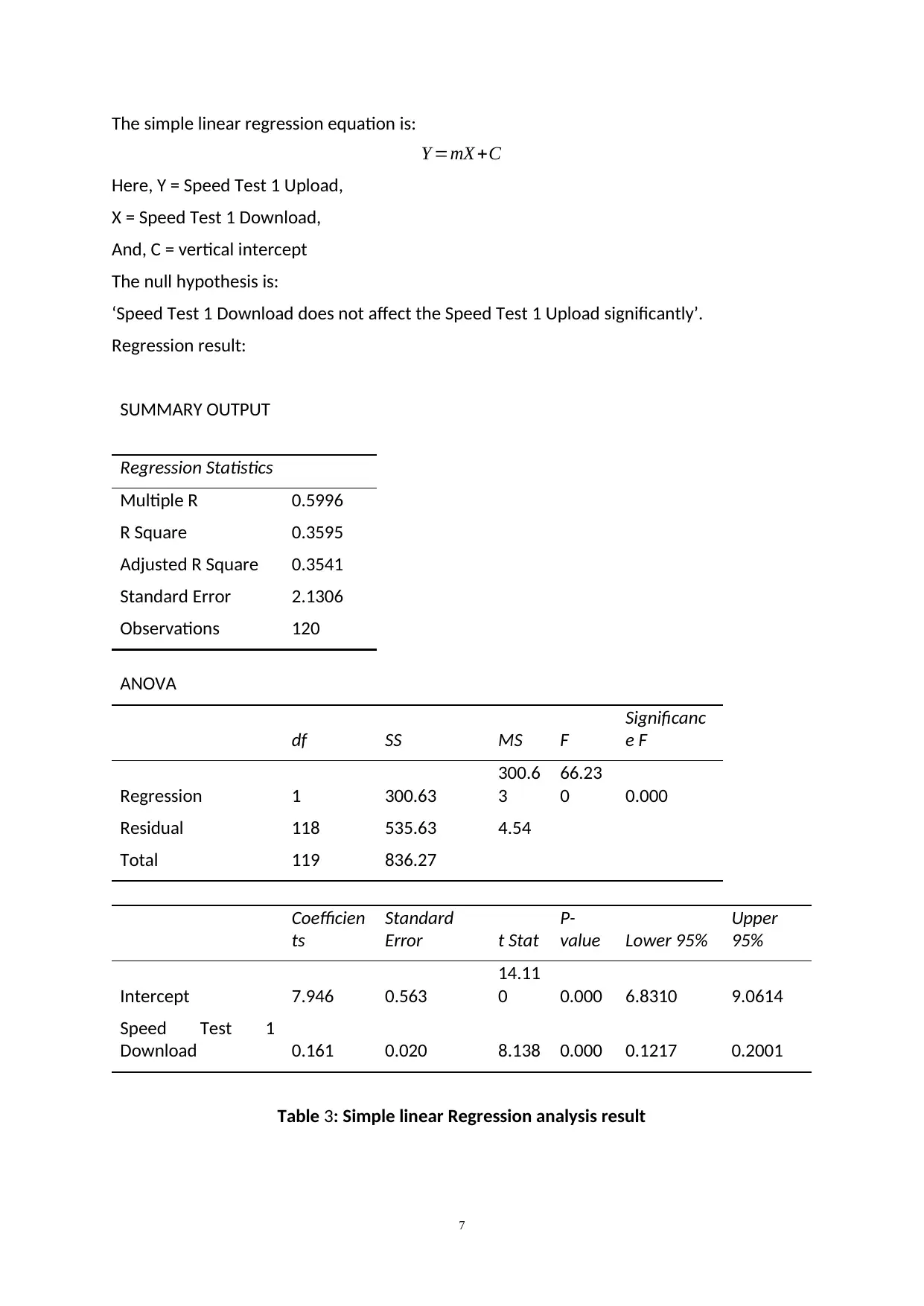
The simple linear regression equation is:
Y =mX +C
Here, Y = Speed Test 1 Upload,
X = Speed Test 1 Download,
And, C = vertical intercept
The null hypothesis is:
‘Speed Test 1 Download does not affect the Speed Test 1 Upload significantly’.
Regression result:
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.5996
R Square 0.3595
Adjusted R Square 0.3541
Standard Error 2.1306
Observations 120
ANOVA
df SS MS F
Significanc
e F
Regression 1 300.63
300.6
3
66.23
0 0.000
Residual 118 535.63 4.54
Total 119 836.27
Coefficien
ts
Standard
Error t Stat
P-
value Lower 95%
Upper
95%
Intercept 7.946 0.563
14.11
0 0.000 6.8310 9.0614
Speed Test 1
Download 0.161 0.020 8.138 0.000 0.1217 0.2001
Table 3: Simple linear Regression analysis result
7

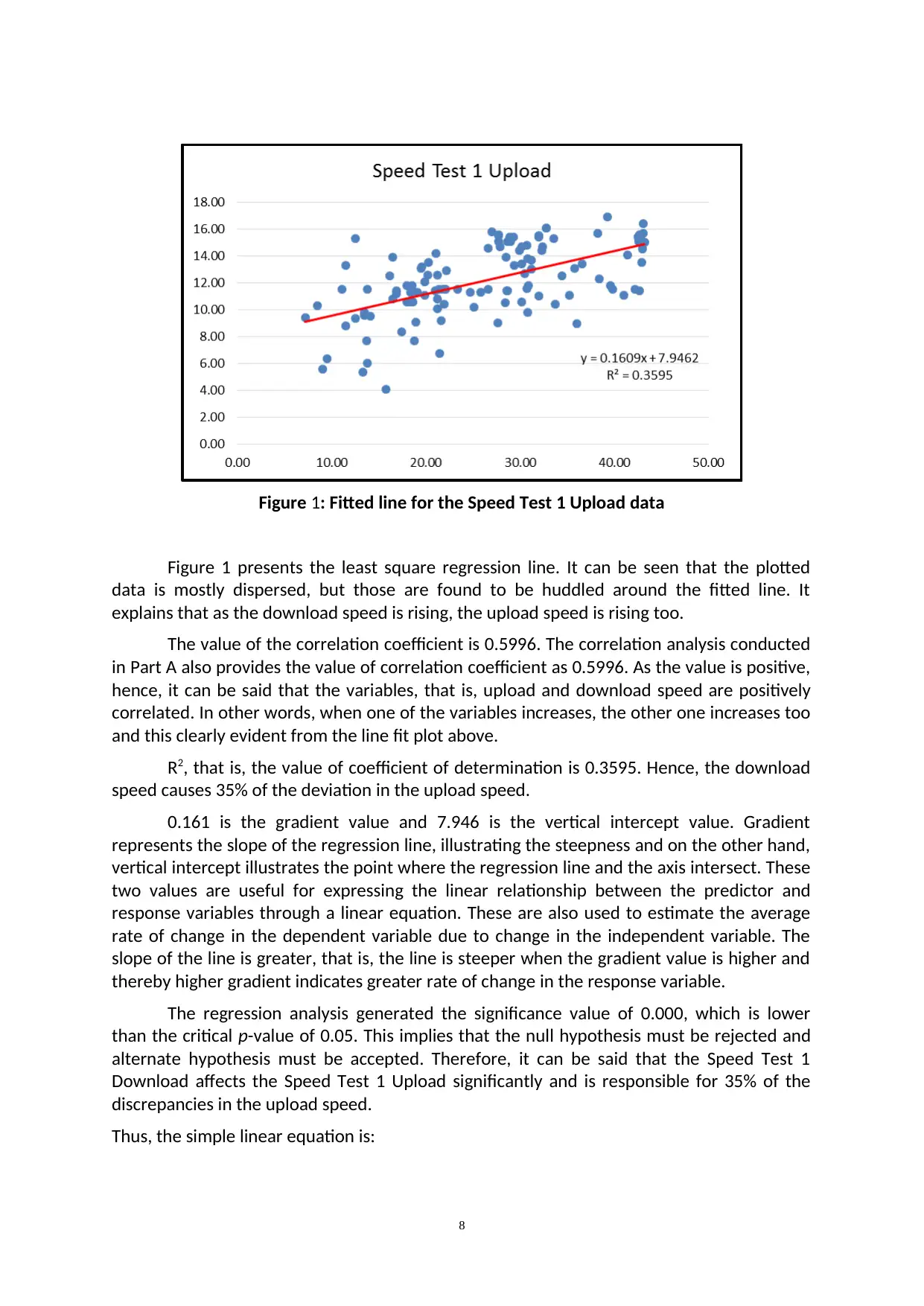
Figure 1: Fitted line for the Speed Test 1 Upload data
Figure 1 presents the least square regression line. It can be seen that the plotted
data is mostly dispersed, but those are found to be huddled around the fitted line. It
explains that as the download speed is rising, the upload speed is rising too.
The value of the correlation coefficient is 0.5996. The correlation analysis conducted
in Part A also provides the value of correlation coefficient as 0.5996. As the value is positive,
hence, it can be said that the variables, that is, upload and download speed are positively
correlated. In other words, when one of the variables increases, the other one increases too
and this clearly evident from the line fit plot above.
R2, that is, the value of coefficient of determination is 0.3595. Hence, the download
speed causes 35% of the deviation in the upload speed.
0.161 is the gradient value and 7.946 is the vertical intercept value. Gradient
represents the slope of the regression line, illustrating the steepness and on the other hand,
vertical intercept illustrates the point where the regression line and the axis intersect. These
two values are useful for expressing the linear relationship between the predictor and
response variables through a linear equation. These are also used to estimate the average
rate of change in the dependent variable due to change in the independent variable. The
slope of the line is greater, that is, the line is steeper when the gradient value is higher and
thereby higher gradient indicates greater rate of change in the response variable.
The regression analysis generated the significance value of 0.000, which is lower
than the critical p-value of 0.05. This implies that the null hypothesis must be rejected and
alternate hypothesis must be accepted. Therefore, it can be said that the Speed Test 1
Download affects the Speed Test 1 Upload significantly and is responsible for 35% of the
discrepancies in the upload speed.
Thus, the simple linear equation is:
8

Speed Test 1 Upload = 0.1609* Speed Test 1 Download + 7.9462
Impact of the Evening time and download speed on the upload speed
For evaluating the influence of two variables, download speed and Evening time
(independent or predictor) on the upload speed (dependent or response variable), multiple
linear regression has been performed.
The equation for the multiple linear regression model is:
Y = β1 X1 + β2 X 2+C
where, Y is the dependent or response variable [ Y = Speed Test 1 Upload],
X is the independent or predictor variable [X1 = Speed Test 1 Download, X2 = Evening]
β is the multiple regression coefficient or gradient,
and, C is the vertical intercept or constant.
The null hypothesis to be evaluated is:
‘Impact of Download speed and time being Evening on the upload speed is not significant’.
Here, ‘Evening’ is a categorical variable. For performing the regression analysis, the
data had to be converted into numeric values using 0 and 1. 0 represents the value ‘Evening’
and 1 represents the value ‘Not Evening’. The result of the multiple linear regression
analysis is provided below.
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.6001
R Square 0.3601
Adjusted R Square 0.3491
Standard Error 2.1387
Observations 120
ANOVA
df SS MS F
Significanc
e F
Regression 2 301.12
150.5
6
32.91
7 0.000
Residual 117 535.15 4.57
Total 119 836.27
9

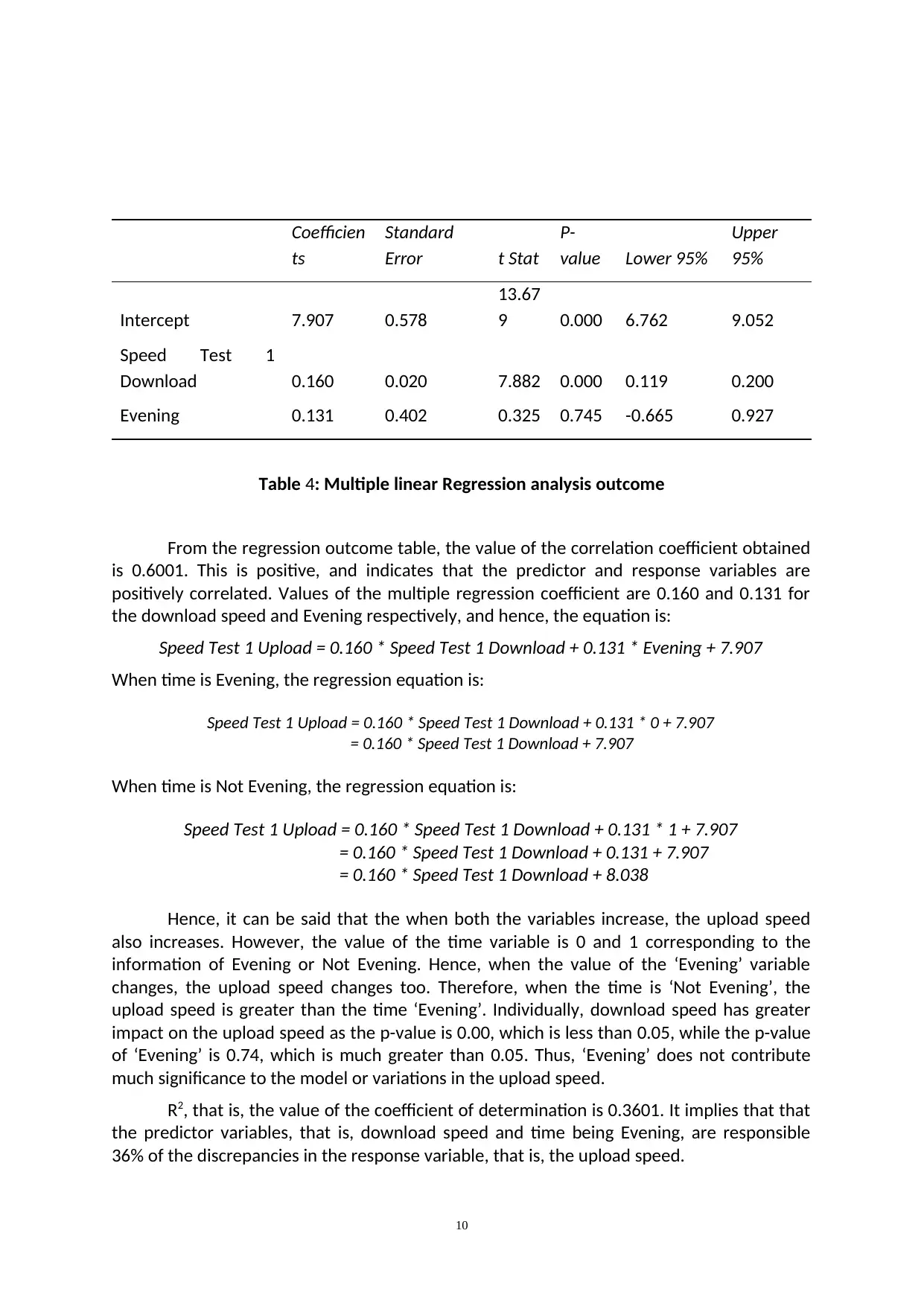
Coefficien
ts
Standard
Error t Stat
P-
value Lower 95%
Upper
95%
Intercept 7.907 0.578
13.67
9 0.000 6.762 9.052
Speed Test 1
Download 0.160 0.020 7.882 0.000 0.119 0.200
Evening 0.131 0.402 0.325 0.745 -0.665 0.927
Table 4: Multiple linear Regression analysis outcome
From the regression outcome table, the value of the correlation coefficient obtained
is 0.6001. This is positive, and indicates that the predictor and response variables are
positively correlated. Values of the multiple regression coefficient are 0.160 and 0.131 for
the download speed and Evening respectively, and hence, the equation is:
Speed Test 1 Upload = 0.160 * Speed Test 1 Download + 0.131 * Evening + 7.907
When time is Evening, the regression equation is:
Speed Test 1 Upload = 0.160 * Speed Test 1 Download + 0.131 * 0 + 7.907
= 0.160 * Speed Test 1 Download + 7.907
When time is Not Evening, the regression equation is:
Speed Test 1 Upload = 0.160 * Speed Test 1 Download + 0.131 * 1 + 7.907
= 0.160 * Speed Test 1 Download + 0.131 + 7.907
= 0.160 * Speed Test 1 Download + 8.038
Hence, it can be said that the when both the variables increase, the upload speed
also increases. However, the value of the time variable is 0 and 1 corresponding to the
information of Evening or Not Evening. Hence, when the value of the ‘Evening’ variable
changes, the upload speed changes too. Therefore, when the time is ‘Not Evening’, the
upload speed is greater than the time ‘Evening’. Individually, download speed has greater
impact on the upload speed as the p-value is 0.00, which is less than 0.05, while the p-value
of ‘Evening’ is 0.74, which is much greater than 0.05. Thus, ‘Evening’ does not contribute
much significance to the model or variations in the upload speed.
R2, that is, the value of the coefficient of determination is 0.3601. It implies that that
the predictor variables, that is, download speed and time being Evening, are responsible
36% of the discrepancies in the response variable, that is, the upload speed.
10

By comparing the outcome of the simple linear regression model and multiple linear
regression model, it is observed that R2 (coefficient of determination) attributes to 35% of
the discrepancies in the upload speed in case of simple linear regression model, while, in
case of the multiple linear regression model, the download speed and time being Evening
(predictor variables) cause 36% of the deviations in the upload speed. Therefore, it can be
said that the multiple linear regression model is a better fit for explaining the discrepancies
in the upload speed. Furthermore, the significance value is lower than 0.05, implying the
null hypothesis to be rejected. Therefore, the download speed and time being Evening have
significant impact on the upload speed of the broadband.
Sincerely,
[Name of the student].
11

Bibliography
Darlington, R.B. and Hayes, A.F., 2016. Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Schroeder, L.D., Sjoquist, D.L. and Stephan, P.E., 2016. Understanding regression analysis:
An introductory guide (Vol. 57). Sage Publications.
Wang, B., Zhou, Z., Wang, H., Tu, X.M. and Feng, C., 2019. The p-value and model
specification in statistics. General psychiatry, 32(3).
12