Quantitative Methods with Economics Project Assignment S1 2019

This project analyzes quantitative methods in economics, focusing on two key problems. The first problem examines the cost, revenue, and profit functions for three types of drone housing (silver, chromium, and titanium), determining break-even points and analyzing the impact of different pricing strategies. The second problem explores demand and supply dynamics, including the impact of a price decrease on equilibrium price, quantity, and restaurant revenue. The project calculates equilibrium points, assesses price elasticity, and evaluates the implications of pricing decisions on profitability. It also considers underlying assumptions and limitations of the analysis, providing a comprehensive economic perspective on the scenarios presented.

QUANTIATIVE
METHODS WITH
ECONOMICS
STUDENT ID:
[Pick the date]

Question 1
The three types of outer housing i.e. silver, chromium and titanium that are used for making
drones. The associated data is represented below.
Silver Chromium Titanium
Cost of metal housing $ 18.00 $ 21.00 $ 26.00
Cost of electric parts $ 12.50 $ 12.50 $ 12.50
Selected sale price $ 37.00 $ 44.00 $ 53.00
Fixed production cost $ 250.00 $ 250.00 $ 250.00
(1) Total cost and total revenue function
Variable cost
Variable cost (VC) = Cost of metal housing + Cost of electric parts
For Silver = 18 + 12.5 = $30.50
For Chromium = 21 + 12.5 = $33.50
For Titanium = 26+ 12.50 = $38.50
Total cost
Total cost (TC) = (Number of units *Variable cost) + Fixed cost
Assuming number of units as Q
For Silver = (Q *30.50) + 250 = 30.50 Q + 250
For Chromium = (Q*33.50) + 250 = 33.50 Q + 250
For Titanium = (Q *38.50) + 250 = 38.50 Q + 250
Total revenue
TR = P*Q
Graphical representation
2

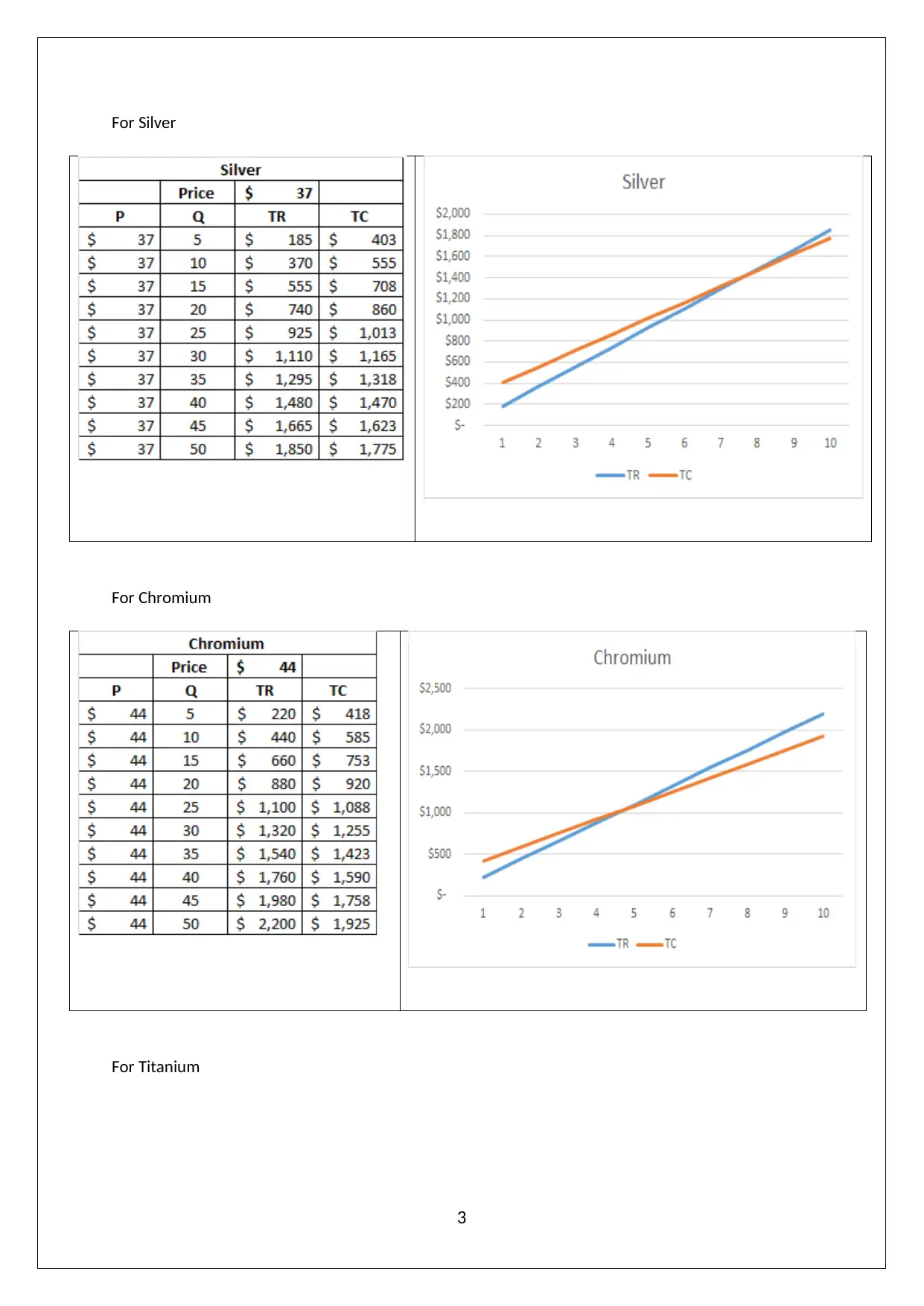
For Silver
For Chromium
For Titanium
3

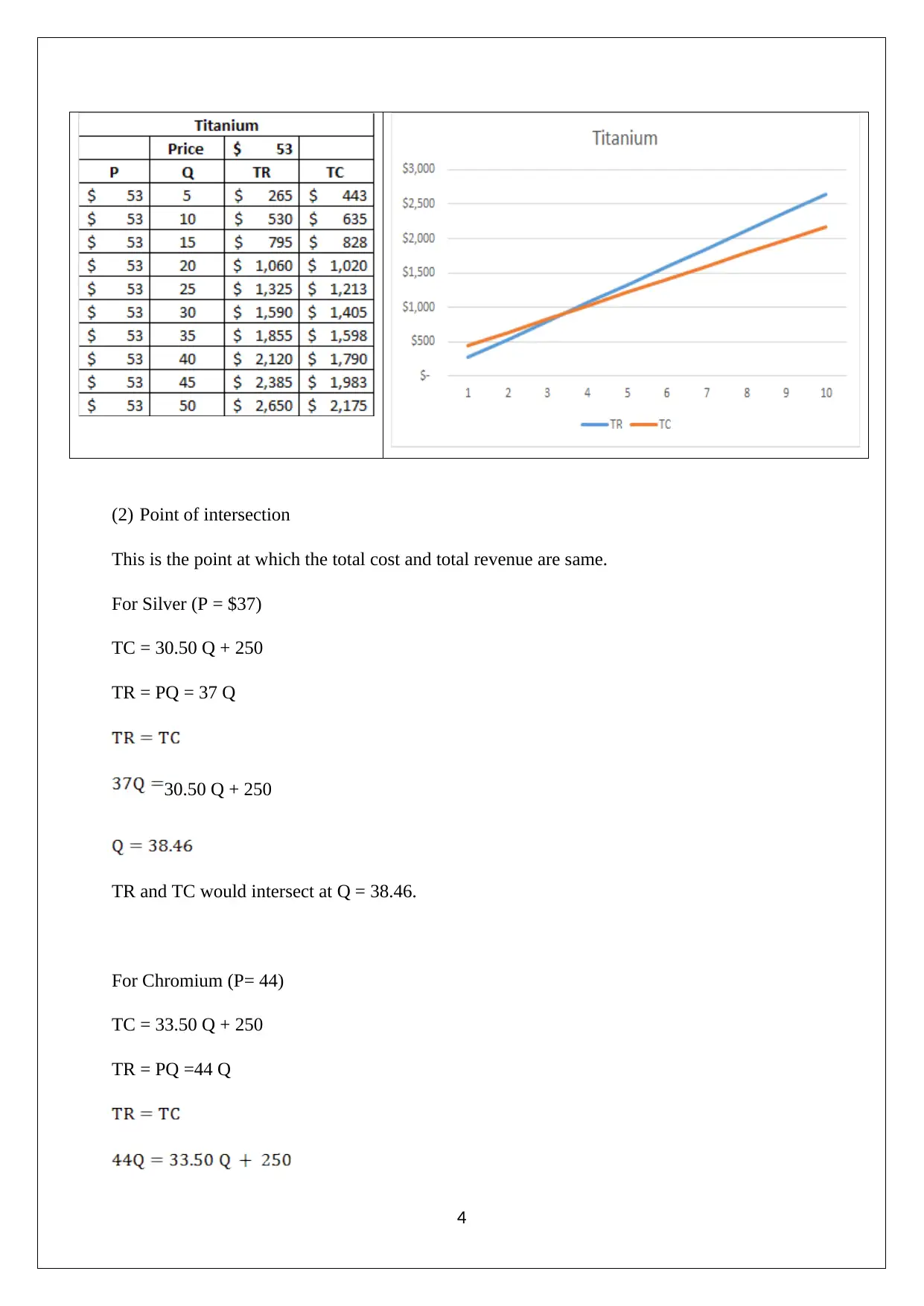
(2) Point of intersection
This is the point at which the total cost and total revenue are same.
For Silver (P = $37)
TC = 30.50 Q + 250
TR = PQ = 37 Q
30.50 Q + 250
TR and TC would intersect at Q = 38.46.
For Chromium (P= 44)
TC = 33.50 Q + 250
TR = PQ =44 Q
4

TR and TC would intersect at Q = 23.81
For Titanium
TC = 38.50 Q + 250
TR = PQ = 53 Q
38.50 Q + 250
TR and TC would intersect at Q = 17.24.
(3) Profit function and break even point
Profit = TR -TC
The TR and TC would be same at the break.
For Silver
TC= 30.50 Q + 250
TR = PQ =37 Q
Profit = TR -PC = 37Q – (30.50 Q + 250) = 6.50Q -250
Breakeven: Q = 38.46.
For Chromium
TC = 33.50 Q + 250
TR = PQ = 44 Q
Profit = TR -PC = 44Q – (33.50 Q + 250) = 10.50 Q -250
5

Breakeven:Q = 23.81
For Titanium
TC = 38.50 Q + 250
TR = PQ = 53 Q
Profit = TR -PC = 53 Q – (38.50 Q + 250) = 14.50 Q -250
Breakeven:Q = 17.24.
4) a) The point of intersection obtained in part (1) and (2) essentially indicate the break even
point. At this point the cost incurred and revenue earned would be equal owing to which the
profit made would be zero. This is significant since this is the minimum sales level that a
business or division would have to achieve so as to avoid losses. Essentially, part (3) is a
different way of computing break even and hence yielded same results as (1) and (2).
b) Considering that the lowest break-even point is for the Titanium variant, hence the
associated profits would be highest for this type of drone. On the other hand, the highest
break-even point is for the Silver variant which implies highest units would have to be sold of
this variant to break even. The Chromium variant lies in between.
c) A key assumption is with regarding the cost structure which is estimated to remain same
and no economies of scale would be realised. Also, it has been assumed that any quantity
produced would be readily sold. A key limitation is that the underlying cost, demand and
cost structure has been taken as constant.
Question 2
Demand equation
Supply equation
Where,
6

(1) The two random numbers i.e. a and b between 0.1 and 0.9 has generatedvia =RAND()
function in the excel.
and
(2) Equilibrium price and equilibrium quantity
Demand equation
Supply equation
At equilibrium the demand and supply would be equal.
Quantity must not be negative and thus, theequilibrium quantity will be 18.57.
Now,
Hence, the equilibrium price will be $29.30.
(3) Updated demand equation which include $15 price decrease
7

Updated demand equation
Here, p would be p-15
Thus, updated demand equation would be p=165-6.5 q.
(4) New equilibrium price and equilibrium quantity
New updated demand equation
Supply equation
At equilibrium the demand and supply would be equal.
Quantity must not be negative and thus, the equilibrium quantity will be 20.714.
Now,
Hence, the equilibrium price will be $30.36.
(5) Demand and supply curve including the updated demand function
8

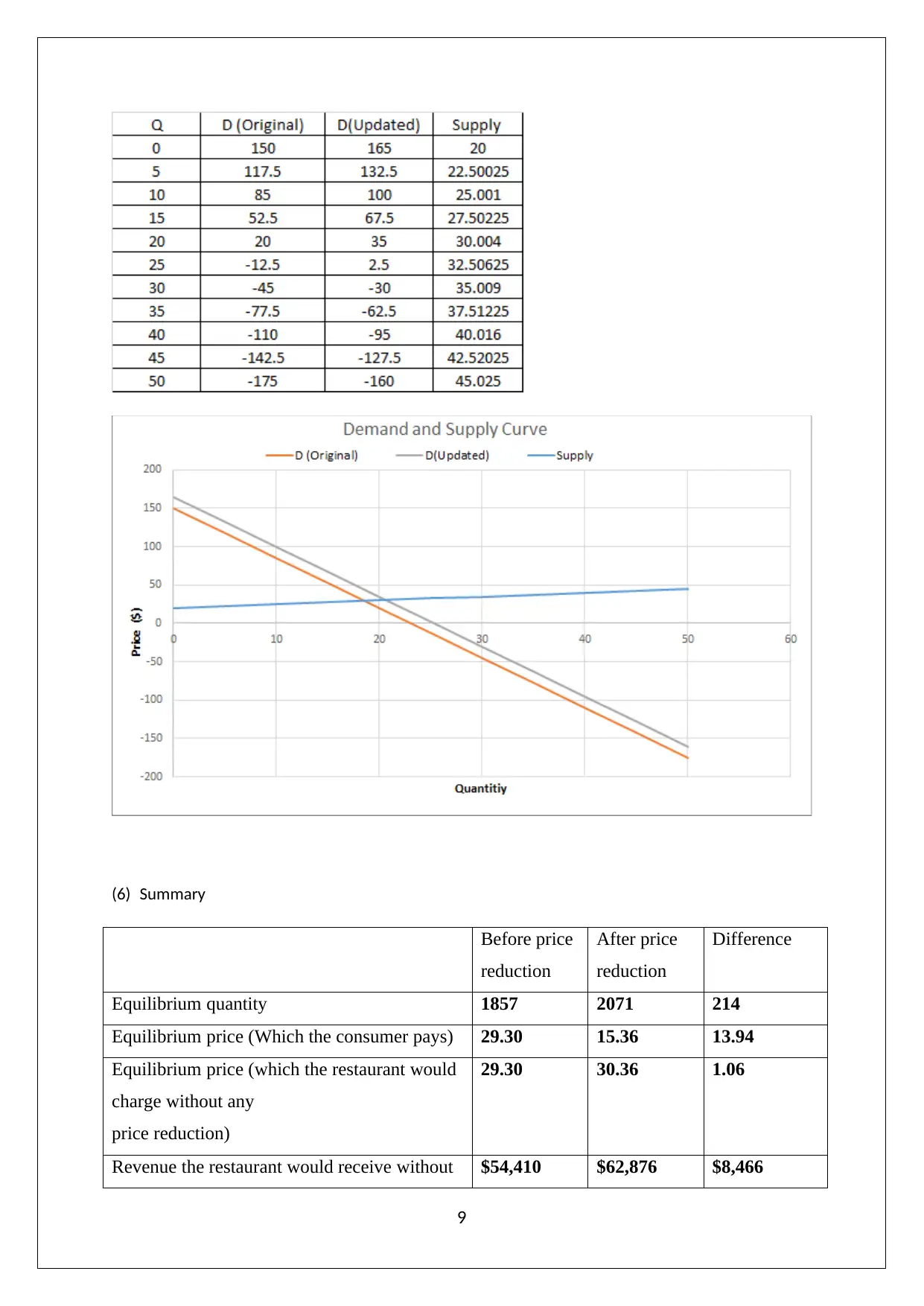
(6) Summary
Before price
reduction
After price
reduction
Difference
Equilibrium quantity 1857 2071 214
Equilibrium price (Which the consumer pays) 29.30 15.36 13.94
Equilibrium price (which the restaurant would
charge without any
price reduction)
29.30 30.36 1.06
Revenue the restaurant would receive without $54,410 $62,876 $8,466
9

any price reduction
Revenue the restaurant receives with the
pricereduction
$54,410 $31,811 -$22,599
(7) Summary conclusion is stated below.
a) Based on the computations above, it is evident that owing to price decrease enacted by the
restaurant, there is increase in the equilibrium price by $1.06 per customer. However, the
price per dinner realised by the restaurant has come down significantly. Also, the increase
in the quantity has not been significant. This clearly reflects that the demand for the
seafood at the restaurant is demand inelastic. The impact on the overall revenue for the
decrease in price has been negative from the perspective of the restaurant.
b) From the above discussion, it is apparent that the seafood demand at the restaurant is
inelastic as the percentage change in quantity is numerically significantly lower than the
drop in price. In such a case, it would make more sense to increase the price rather than
lowering the price. Thus, it seems that the restaurant has a fixed customer base who tend
to appreciate the seafood served. These customers are loyal while the other those who do
not come are not driven by price as lower price has not been successful in attracting them.
Hence, price should not be lowered.
c) It has been assumed that the taste and preferences of the customers do not change.
Further, it is also assumed that the demand and supply function do not alter. This is
because if any of the function is altered, then the reliability of the analysis would be
compromised. A key shortcoming of the analysis is the assumption about demand and
supply function to remain static which is rarely the case.
10