MAT111A College Algebra: Quadratic Equations, Functions and Graphs
VerifiedAdded on 2023/06/11
|12
|1356
|385
Homework Assignment
AI Summary
This assignment solution covers several key concepts in College Algebra. It begins by identifying the equation of a quadratic function from its graph and finding the vertex of a parabola. The solution demonstrates how to sketch the graph of a quadratic function using its vertex and intercepts, and how to determine its axis of symmetry, domain, and range. It also includes problems involving the maximum height of a projectile and determining when it hits the ground. The assignment further explores polynomial functions, including identifying the degree, leading term, and end behavior of their graphs, as well as finding x and y intercepts. Finally, the solution covers rational functions, including finding vertical and horizontal asymptotes, and graphing transformations. Desklib offers numerous resources for students, including past papers and solved assignments to aid in their understanding of these concepts.

Running head: COLLEGE ALGEBRA 1
College Algebra
Name
Institution
College Algebra
Name
Institution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
COLLEGE ALGEBRA 2
Question 1
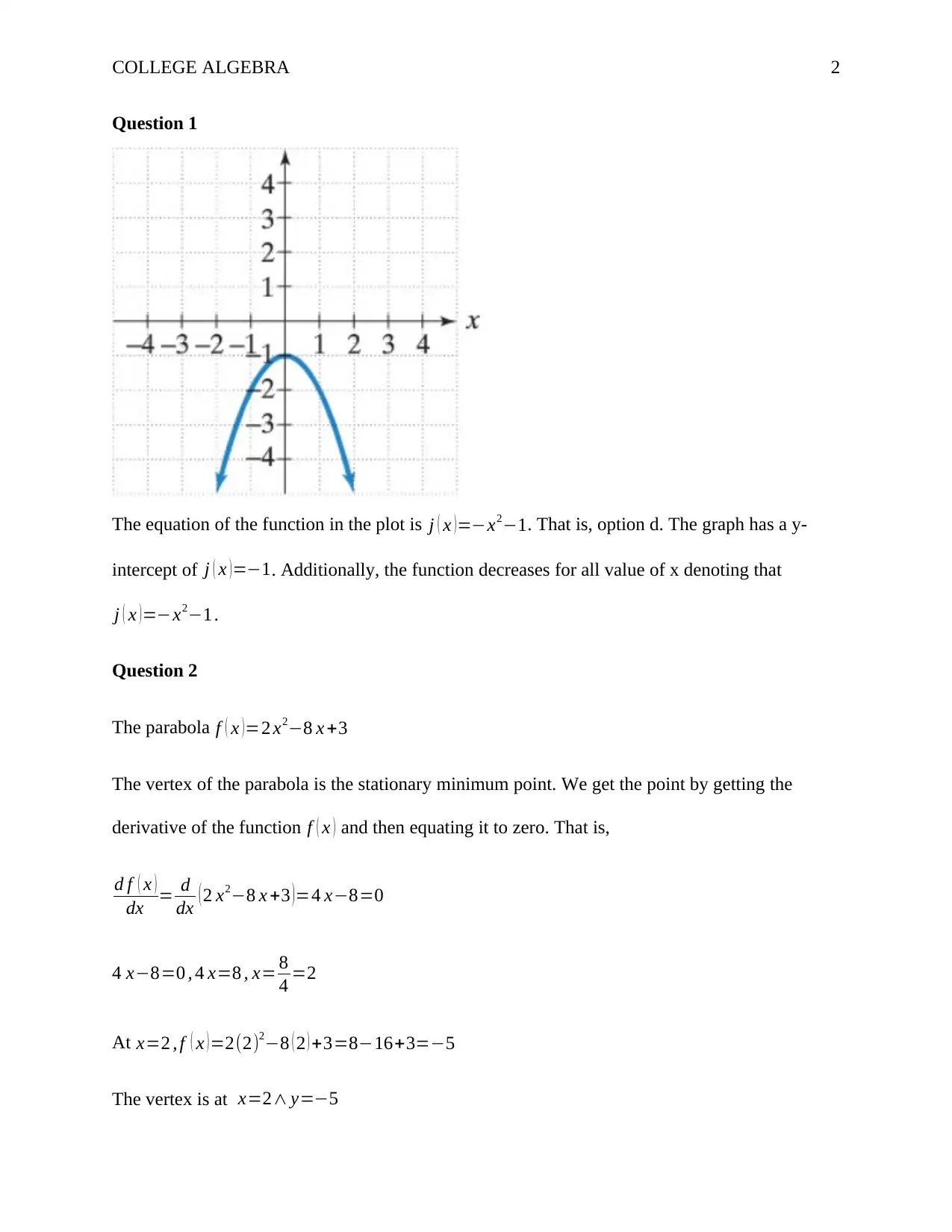
The equation of the function in the plot is j ( x )=−x2−1. That is, option d. The graph has a y-
intercept of j ( x )=−1. Additionally, the function decreases for all value of x denoting that
j ( x )=−x2−1 .
Question 2
The parabola f ( x )=2 x2−8 x +3
The vertex of the parabola is the stationary minimum point. We get the point by getting the
derivative of the function f ( x ) and then equating it to zero. That is,
d f ( x )
dx = d
dx ( 2 x2−8 x +3 )=4 x−8=0
4 x−8=0 , 4 x=8 , x= 8
4 =2
At x=2 , f ( x )=2(2)2−8 ( 2 ) +3=8−16+3=−5
The vertex is at x=2∧ y=−5
Question 1
The equation of the function in the plot is j ( x )=−x2−1. That is, option d. The graph has a y-
intercept of j ( x )=−1. Additionally, the function decreases for all value of x denoting that
j ( x )=−x2−1 .
Question 2
The parabola f ( x )=2 x2−8 x +3
The vertex of the parabola is the stationary minimum point. We get the point by getting the
derivative of the function f ( x ) and then equating it to zero. That is,
d f ( x )
dx = d
dx ( 2 x2−8 x +3 )=4 x−8=0
4 x−8=0 , 4 x=8 , x= 8
4 =2
At x=2 , f ( x )=2(2)2−8 ( 2 ) +3=8−16+3=−5
The vertex is at x=2∧ y=−5

COLLEGE ALGEBRA 3
Question 3
Part a
f ( x )=4−(x −1)2
f ( x )=4− ( x2−2 x+1 ) =3−x2 +2 x
We have the vertex when, d f ( x )
dx =0.That is ,
d
dx (3−x2 +2 x )=−2 x+ 2=0
−2 x+2=0 , 2 x=2, x= 2
2 =1
When x=1 , f ( x )=4− (1−1 )2=4
The vertex is at the point (1 , 4)
The y-intercept is f ( 0 ) =4− ( 0−1 ) 2=4−1=3
The x-intercept is f ( x )=3−x2+ 2 x=−x2 +2 x+ 3=0
x=−2 ± √ 22 −4 (−1 ×3)¿ ¿
2(−1)=−2 ± √ 16
−2 =−2 ± 4
−2 =1±−2
x=1+ (−2 ) =−1∨x=1−−2=3
Using the obtained vertex and intercepts, we can plot the graph of the function as shown in the
figure below.
Question 3
Part a
f ( x )=4−(x −1)2
f ( x )=4− ( x2−2 x+1 ) =3−x2 +2 x
We have the vertex when, d f ( x )
dx =0.That is ,
d
dx (3−x2 +2 x )=−2 x+ 2=0
−2 x+2=0 , 2 x=2, x= 2
2 =1
When x=1 , f ( x )=4− (1−1 )2=4
The vertex is at the point (1 , 4)
The y-intercept is f ( 0 ) =4− ( 0−1 ) 2=4−1=3
The x-intercept is f ( x )=3−x2+ 2 x=−x2 +2 x+ 3=0
x=−2 ± √ 22 −4 (−1 ×3)¿ ¿
2(−1)=−2 ± √ 16
−2 =−2 ± 4
−2 =1±−2
x=1+ (−2 ) =−1∨x=1−−2=3
Using the obtained vertex and intercepts, we can plot the graph of the function as shown in the
figure below.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
COLLEGE ALGEBRA 4
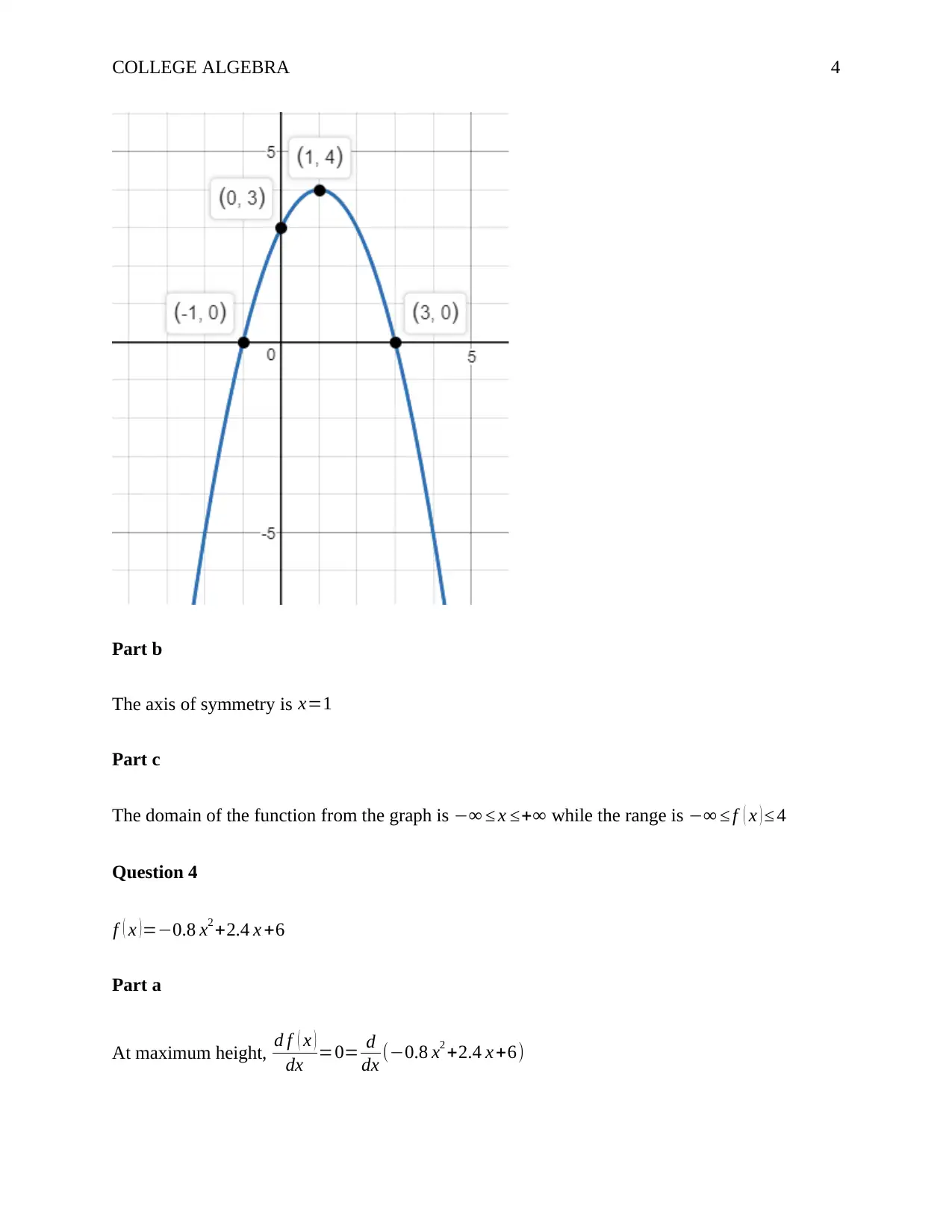
Part b
The axis of symmetry is x=1
Part c
The domain of the function from the graph is −∞ ≤ x ≤+∞ while the range is −∞ ≤ f ( x ) ≤ 4
Question 4
f ( x ) =−0.8 x2 +2.4 x +6
Part a
At maximum height, d f ( x )
dx =0= d
dx (−0.8 x2 +2.4 x +6)
Part b
The axis of symmetry is x=1
Part c
The domain of the function from the graph is −∞ ≤ x ≤+∞ while the range is −∞ ≤ f ( x ) ≤ 4
Question 4
f ( x ) =−0.8 x2 +2.4 x +6
Part a
At maximum height, d f ( x )
dx =0= d
dx (−0.8 x2 +2.4 x +6)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

COLLEGE ALGEBRA 5
d
dx (−0.8 x2+ 2.4 x+ 6 ) =−1.6 x+2.4=0
1.6 x=2.4 , x= 2.4
1.6 =1.5
When x=1.5 , f ( x )=−0.8(1.5)2+2.4 ( 1.5 )+ 6=7.8
The ball reaches a maximum height of 7.8 feet which occurs at 7.8−6=1.8 feetfrom where it
was thrown.
Part b
Given f ( x ) =−0.8 x2 +2.4 x +6 , the ball touchesthe ground when f ( x ) =0
−0.8 x2+ 2.4 x+ 6=0
x=−2.4 ± √2.42−4 (−0.8 ×6)¿ ¿
2(−0.8)=−2.4 ± √24.96
−1.6 =−2 .4 ± 4.996
−1.6 =1.5 ±−3.122
x=1 .5+ (−3.122 )=−1.622 ( negative ignored )∨x =1.5−−3.122=4.622≅ 4.6
Thus, the ball travels 4.6 feet horizontally before touching the ground.
Part c
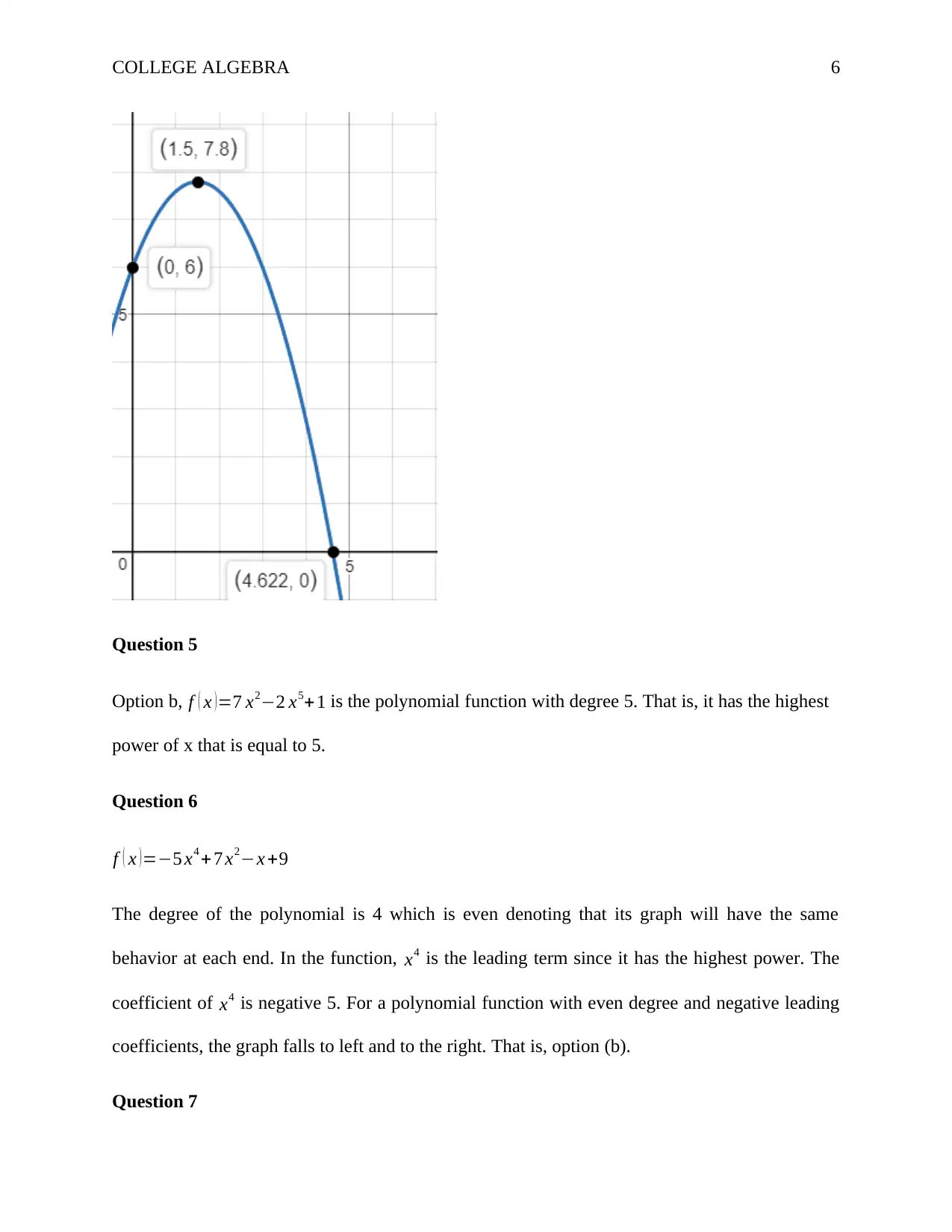
The graph of the function f ( x )=−0.8 x2 +2.4 x +6 is shown below.
d
dx (−0.8 x2+ 2.4 x+ 6 ) =−1.6 x+2.4=0
1.6 x=2.4 , x= 2.4
1.6 =1.5
When x=1.5 , f ( x )=−0.8(1.5)2+2.4 ( 1.5 )+ 6=7.8
The ball reaches a maximum height of 7.8 feet which occurs at 7.8−6=1.8 feetfrom where it
was thrown.
Part b
Given f ( x ) =−0.8 x2 +2.4 x +6 , the ball touchesthe ground when f ( x ) =0
−0.8 x2+ 2.4 x+ 6=0
x=−2.4 ± √2.42−4 (−0.8 ×6)¿ ¿
2(−0.8)=−2.4 ± √24.96
−1.6 =−2 .4 ± 4.996
−1.6 =1.5 ±−3.122
x=1 .5+ (−3.122 )=−1.622 ( negative ignored )∨x =1.5−−3.122=4.622≅ 4.6
Thus, the ball travels 4.6 feet horizontally before touching the ground.
Part c
The graph of the function f ( x )=−0.8 x2 +2.4 x +6 is shown below.
COLLEGE ALGEBRA 6
Question 5
Option b, f ( x )=7 x2−2 x5+ 1 is the polynomial function with degree 5. That is, it has the highest
power of x that is equal to 5.
Question 6
f ( x )=−5 x4 + 7 x2−x +9
The degree of the polynomial is 4 which is even denoting that its graph will have the same
behavior at each end. In the function, x4 is the leading term since it has the highest power. The
coefficient of x4 is negative 5. For a polynomial function with even degree and negative leading
coefficients, the graph falls to left and to the right. That is, option (b).
Question 7
Question 5
Option b, f ( x )=7 x2−2 x5+ 1 is the polynomial function with degree 5. That is, it has the highest
power of x that is equal to 5.
Question 6
f ( x )=−5 x4 + 7 x2−x +9
The degree of the polynomial is 4 which is even denoting that its graph will have the same
behavior at each end. In the function, x4 is the leading term since it has the highest power. The
coefficient of x4 is negative 5. For a polynomial function with even degree and negative leading
coefficients, the graph falls to left and to the right. That is, option (b).
Question 7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

COLLEGE ALGEBRA 7
Part a
f ( x ) =−x4 +4 x2
The degree of the polynomial is 4 which is even denoting that its graph will have the same
behavior at each end. In the function, x4 is the leading term since it has the highest power. The
coefficient of x4 is -1. For a polynomial function with an even degree and a negative leading
coefficient, the graph falls to left and to the right.
Part b
The x-intercepts f ( x ) =−x4 +4 x2 occurs when f ( x )=0
f ( x )=−x4 +4 x2=0
−x4 + 4 x2=x2(−x¿ ¿2+4)=0¿
x2=0 , x=0
¿ ¿
The x-intercepts are x=0 ,∨x=−2∨x =+ 2
The graph touches the x-axis and turns around at x=0 but crosses the x-axis when
x=−2∧x=+2.
Part c
The y-intercept is f ( x=0 ) =−04 + 4(0)2=0
Part d
The graph of f ( x ) =−x4 +4 x2 has y-axis symmetry.
Part a
f ( x ) =−x4 +4 x2
The degree of the polynomial is 4 which is even denoting that its graph will have the same
behavior at each end. In the function, x4 is the leading term since it has the highest power. The
coefficient of x4 is -1. For a polynomial function with an even degree and a negative leading
coefficient, the graph falls to left and to the right.
Part b
The x-intercepts f ( x ) =−x4 +4 x2 occurs when f ( x )=0
f ( x )=−x4 +4 x2=0
−x4 + 4 x2=x2(−x¿ ¿2+4)=0¿
x2=0 , x=0
¿ ¿
The x-intercepts are x=0 ,∨x=−2∨x =+ 2
The graph touches the x-axis and turns around at x=0 but crosses the x-axis when
x=−2∧x=+2.
Part c
The y-intercept is f ( x=0 ) =−04 + 4(0)2=0
Part d
The graph of f ( x ) =−x4 +4 x2 has y-axis symmetry.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
COLLEGE ALGEBRA 8
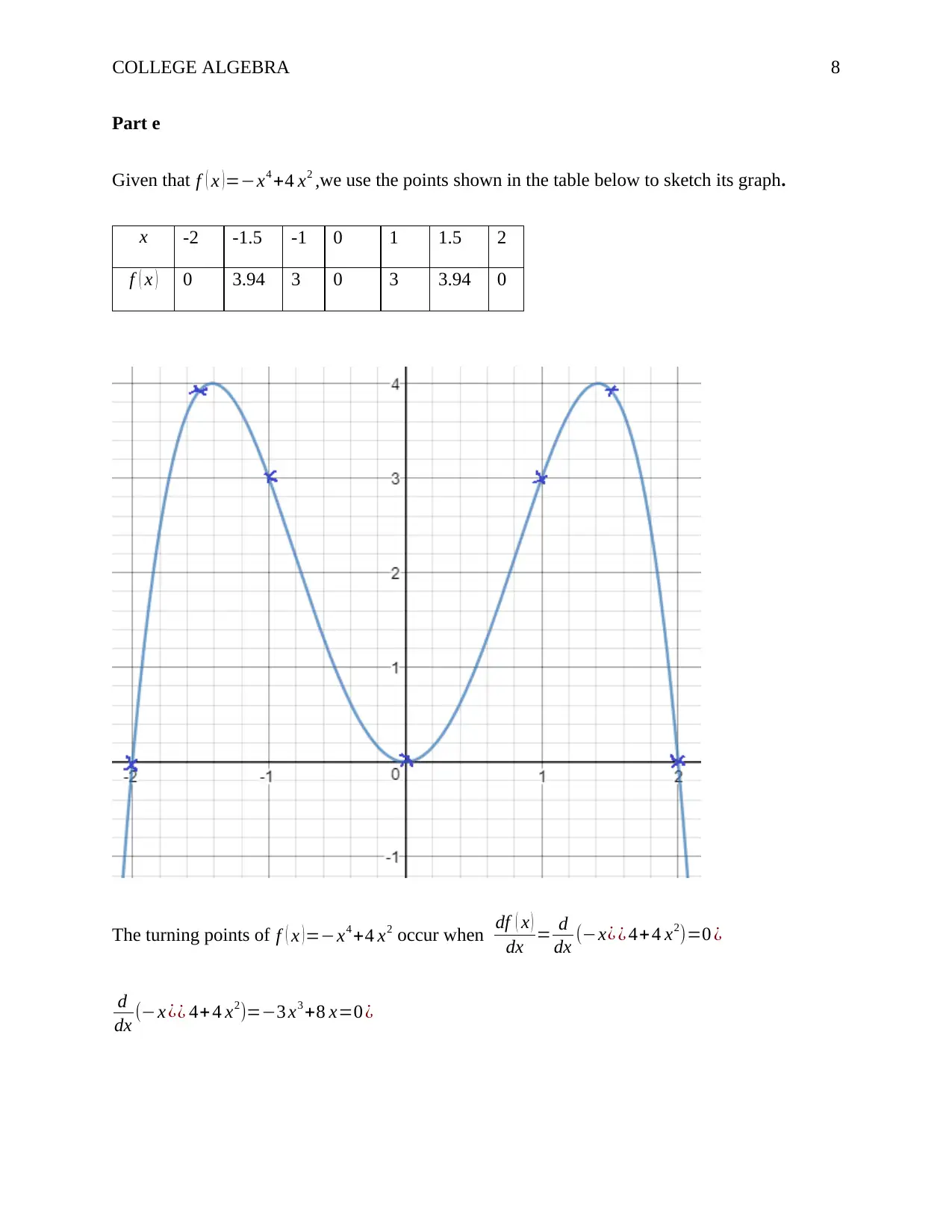
Part e
Given that f ( x ) =−x4 +4 x2 ,we use the points shown in the table below to sketch its graph.
x -2 -1.5 -1 0 1 1.5 2
f ( x ) 0 3.94 3 0 3 3.94 0
The turning points of f ( x )=−x4 +4 x2 occur when df ( x )
dx = d
dx (−x¿ ¿ 4+4 x2)=0 ¿
d
dx (−x ¿¿ 4+ 4 x2)=−3 x3 +8 x=0 ¿
Part e
Given that f ( x ) =−x4 +4 x2 ,we use the points shown in the table below to sketch its graph.
x -2 -1.5 -1 0 1 1.5 2
f ( x ) 0 3.94 3 0 3 3.94 0
The turning points of f ( x )=−x4 +4 x2 occur when df ( x )
dx = d
dx (−x¿ ¿ 4+4 x2)=0 ¿
d
dx (−x ¿¿ 4+ 4 x2)=−3 x3 +8 x=0 ¿

COLLEGE ALGEBRA 9
The highest power of df ( x )
dx is 3 implying that f ( x ) has 3 stationary points denoting that the graph
is drawn correctly.
Question 8
Question 9
❑
❑
❑
❑ =x2+x−3− 12
x2 + x−2
Therefore, the quotient is x2+ x−3 while the remainder is −12
Question 10
(x ¿¿ 2−5 x−5 x3+ x4)÷(5+ x )¿
We write the polynomial in descending order to obtain,
(x ¿¿ 2−5 x−5 x3+ x4)÷(5+ x )=x4 −5 x3 + x2−5 x ¿ ÷( x +5)
The highest power of df ( x )
dx is 3 implying that f ( x ) has 3 stationary points denoting that the graph
is drawn correctly.
Question 8
Question 9
❑
❑
❑
❑ =x2+x−3− 12
x2 + x−2
Therefore, the quotient is x2+ x−3 while the remainder is −12
Question 10
(x ¿¿ 2−5 x−5 x3+ x4)÷(5+ x )¿
We write the polynomial in descending order to obtain,
(x ¿¿ 2−5 x−5 x3+ x4)÷(5+ x )=x4 −5 x3 + x2−5 x ¿ ÷( x +5)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

COLLEGE ALGEBRA 10
Question 11
Question 12
Question 13
g ( x )= x−3
x2−9
g ( x ) = x−3
x2−9 = x−3
( x−3)( x +3)= 1
x +3
as x →−3 , g ( −3 ) = 1
−3+3 =∞
Therefore, the function has a vertical asymptote x=−3. However, there are no holes.
Question 14
g ( x ) = 12 x2
3 x2 +1
Question 11
Question 12
Question 13
g ( x )= x−3
x2−9
g ( x ) = x−3
x2−9 = x−3
( x−3)( x +3)= 1
x +3
as x →−3 , g ( −3 ) = 1
−3+3 =∞
Therefore, the function has a vertical asymptote x=−3. However, there are no holes.
Question 14
g ( x ) = 12 x2
3 x2 +1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

COLLEGE ALGEBRA 11
Evidently the leading terms in the numerator and denominator have the same degree. That is,
degree 2. We get the horizontal asymptote by dividing the leading terms to obtain,
y= 12 x2
3 x2 =4
Therefore, the horizontal asymptote is y=4
Question 15
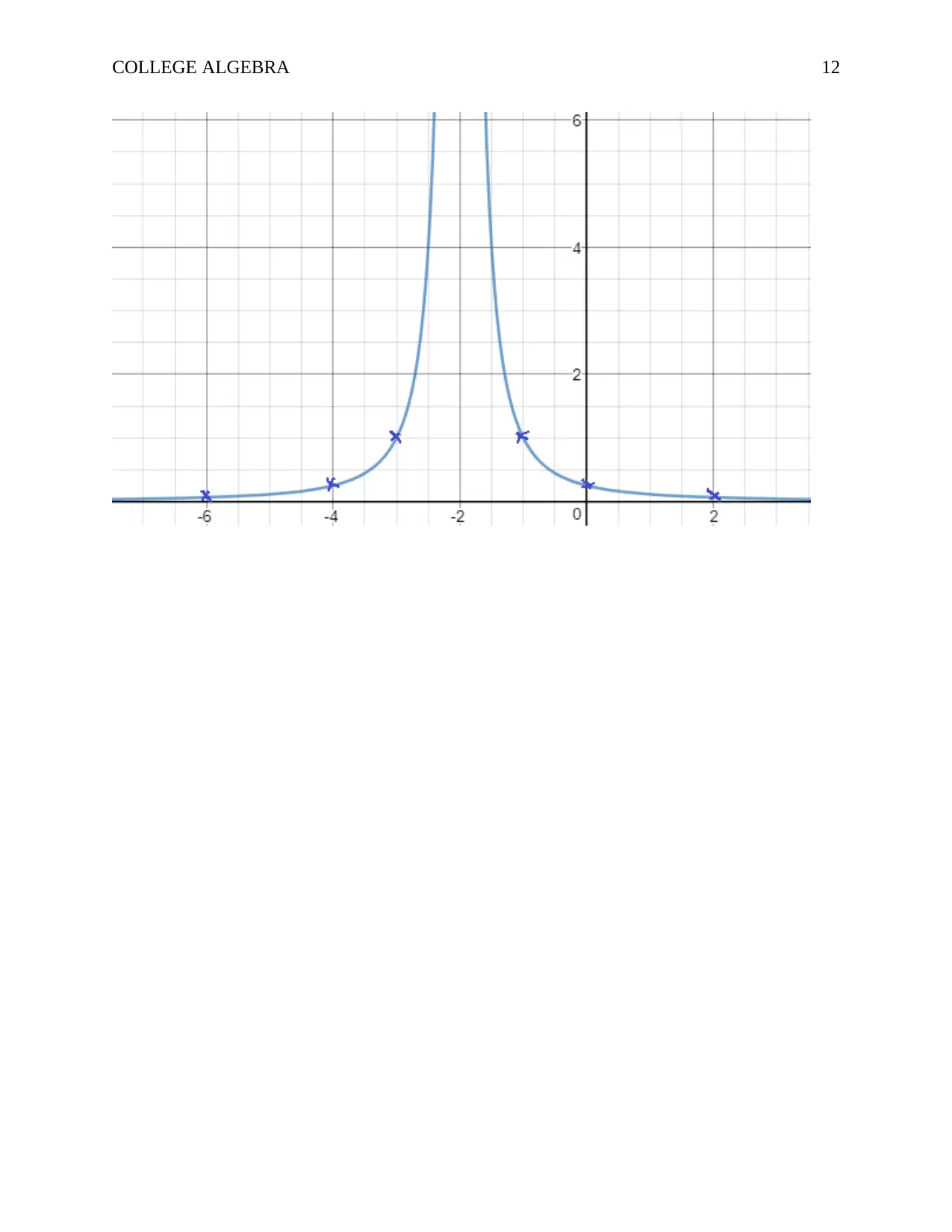
g ( x ) = 1
(x +2)2
To obtain g ( x )= 1
(x +2)2 from f ( x )= 1
x2
First, we draw f ( x )= 1
x2 followed a shift of 2 units to the left. The graph of g ( x ) is shown below.
x -6 -4 -3 -2 -1 0 2
g(x) 0.063 0.25 1 ∞ 1 0.25 0.063
Evidently the leading terms in the numerator and denominator have the same degree. That is,
degree 2. We get the horizontal asymptote by dividing the leading terms to obtain,
y= 12 x2
3 x2 =4
Therefore, the horizontal asymptote is y=4
Question 15
g ( x ) = 1
(x +2)2
To obtain g ( x )= 1
(x +2)2 from f ( x )= 1
x2
First, we draw f ( x )= 1
x2 followed a shift of 2 units to the left. The graph of g ( x ) is shown below.
x -6 -4 -3 -2 -1 0 2
g(x) 0.063 0.25 1 ∞ 1 0.25 0.063
COLLEGE ALGEBRA 12
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





