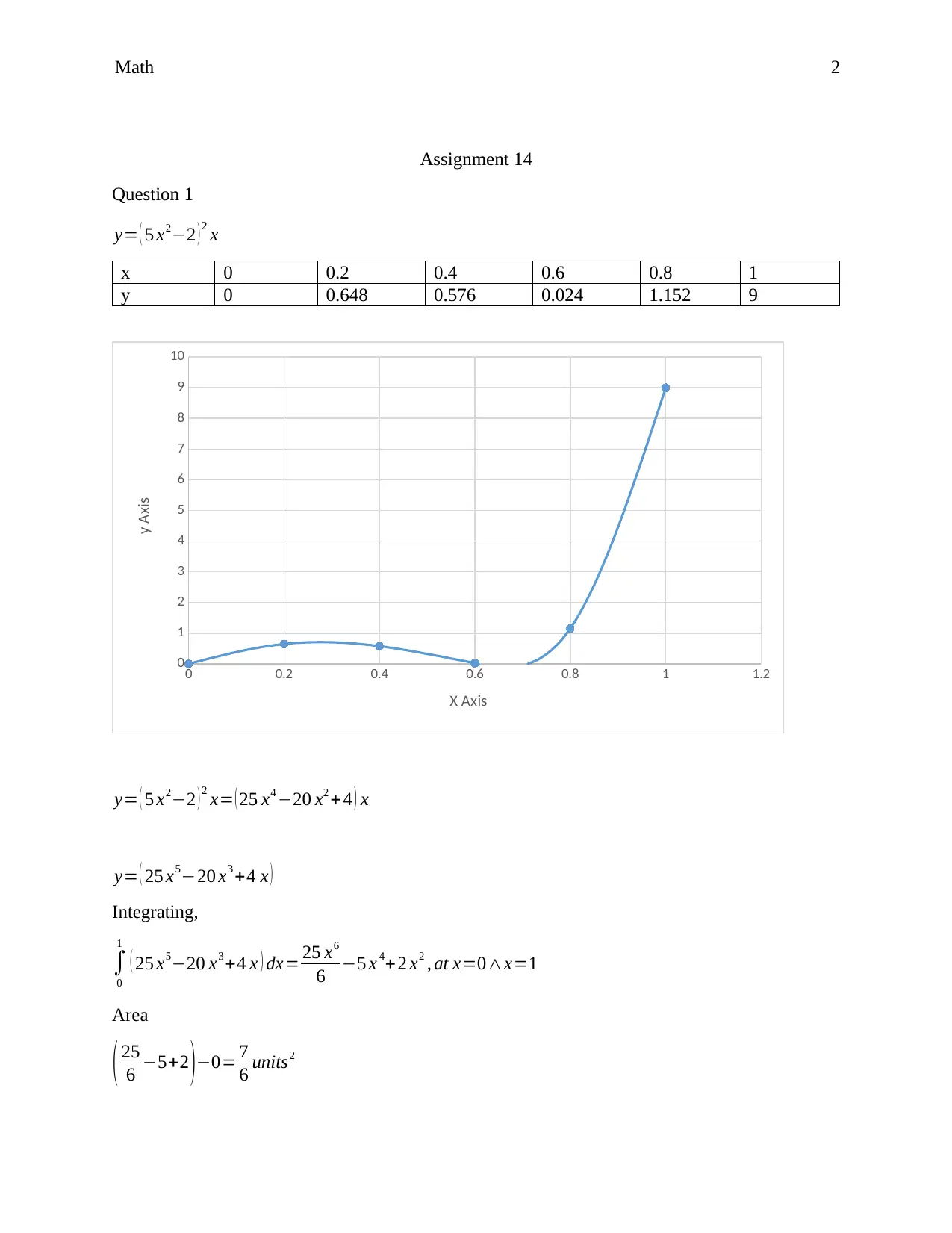
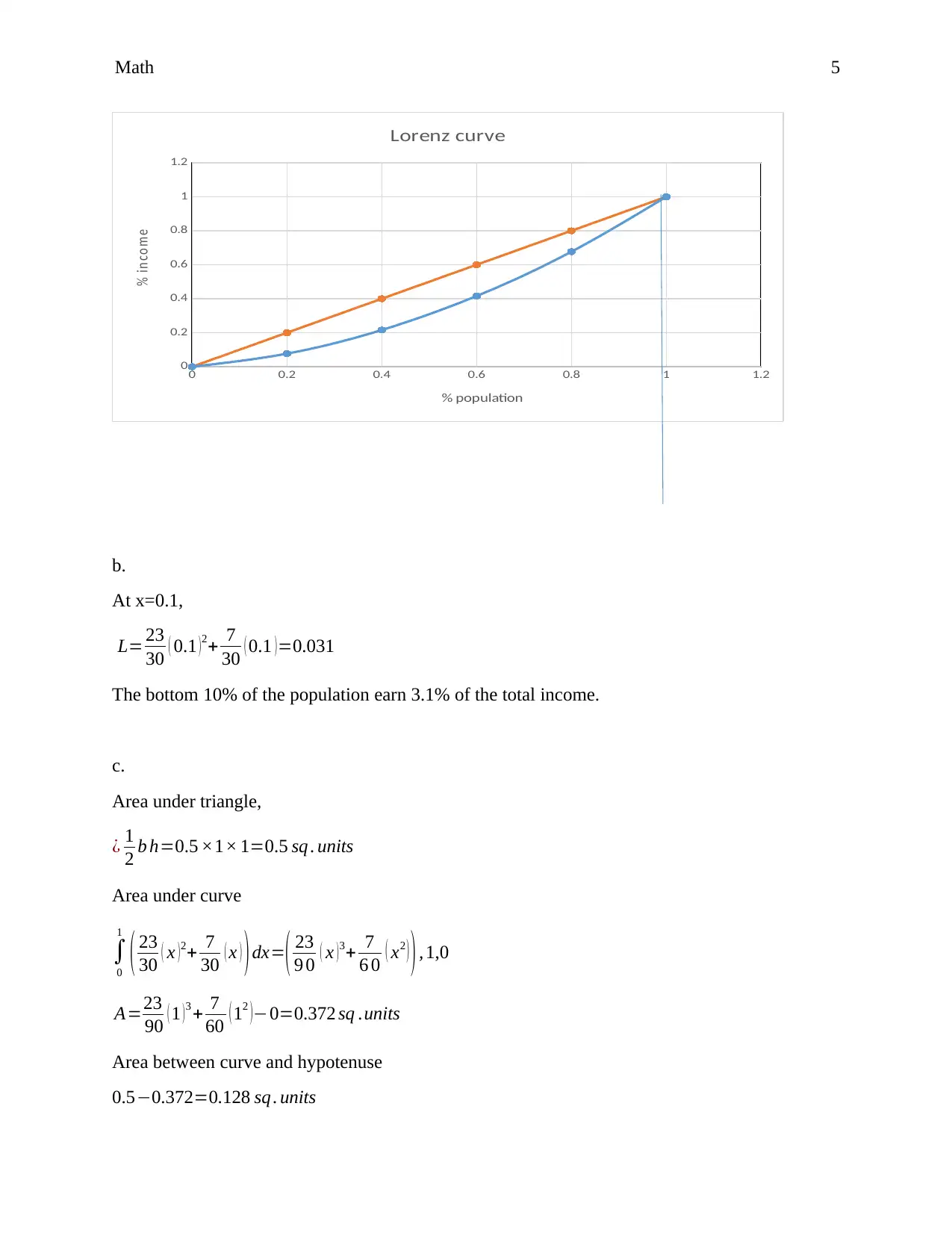
Calculus Assignment MAT 142: Integration, Area, and Lorenz Curve

This assignment consists of two parts: calculus problems and Lorenz curve analysis. The calculus problems involve finding areas under curves using integration and the Fundamental Theorem of Calculus, as well as computing indefinite integrals using the power rule. Specific functions are provided, and the solutions include step-by-step calculations. The Lorenz curve analysis involves sketching a Lorenz curve for a given function, computing and interpreting L(0.10), calculating the Gini coefficient of inequality, and finding a real-world Lorenz curve with a brief description. The assignment uses concepts from calculus and applies them to economic inequality.

Running Head: MATH 1
Mathematics Assignment
Student’s Name
Institutional Affiliation

Math 2
Assignment 14
Question 1
y= ( 5 x2−2 ) 2
x
x 0 0.2 0.4 0.6 0.8 1
y 0 0.648 0.576 0.024 1.152 9
0 0.2 0.4 0.6 0.8 1 1.2
0
1
2
3
4
5
6
7
8
9
10
X Axis
y Axis
y= ( 5 x2−2 ) 2
x= ( 25 x4 −20 x2 + 4 ) x
y= ( 25 x5−20 x3 +4 x )
Integrating,
∫
0
1
( 25 x5−20 x3 +4 x ) dx= 25 x6
6 −5 x 4+ 2 x2 , at x=0∧x=1
Area
( 25
6 −5+2 )−0= 7
6 units2

Math 3
Question 2
y=5 x−1
x 1 1.5 2 e=2.718
y 5 3.33 2.5 1.839
0.5 1 1.5 2 2.5 3
0
1
2
3
4
5
6
Area under the curve
X Axis
Y Axis
Integrating
∫
1
e
(5 x¿¿−1) dx=¿ ln 5 x at x=1∧e ¿ ¿
Therefore, area under the curve
ln 5 ( e )−ln 5=1units2
Question 3
∫ 3 x
x2+ 8 dx=∫3 x ∙ ( x2 +8 )−1
dx
let u= ( x2 +8 )
du
dx =2 x
Therefore,
du
2 =xdx

Math 4
∫3 x ∙ ( x2 +8 )
−1
dx=∫3 ∙ ( u ) −1 xdx
But , xdx = du
2
∫3 ∙ ( u )−1 du
2 =1.5 ln u+C=1.5 ln ( x2 +8 ) +C
Question 4
∫12 x √ 2 x2 +7 dx=∫12 x (2 x2 +7)
1
2 dx
Let , 2 x2 +7=u
du
dx =4 x
Therefore,
du
4 =xdx
∫12 x (2 x2 +7)
1
2 dx =∫ 12 x (u)
1
2 dx
But , xdx = du
4
∫3 (u)
1
2 du=2(u)
3
2 +C=2(2 x2 +7)
3
2 + C
Assignment 15
x 0 0.2 0.4 0.6 0.8 1
L 0 0.077 0.216 0.416 0.677 1

Math 5
0 0.2 0.4 0.6 0.8 1 1.2
0
0.2
0.4
0.6
0.8
1
1.2
Lorenz curve
% population
% in co m e
b.
At x=0.1,
L= 23
30 ( 0.1 )2+ 7
30 ( 0.1 )=0.031
The bottom 10% of the population earn 3.1% of the total income.
c.
Area under triangle,
¿ 1
2 b h=0.5 ×1× 1=0.5 sq . units
Area under curve
∫
0
1
( 23
30 ( x ) 2+ 7
30 ( x ) ) dx=( 23
9 0 ( x ) 3+ 7
6 0 ( x2 ) ) , 1,0
A=23
90 ( 1 )3 + 7
60 ( 12 )−0=0.372 sq .units
Area between curve and hypotenuse
0.5−0.372=0.128 sq . units

Math 6
Gini coefficient = Areabetween curve∧hypotenuse
Areaof triangle = 0.128
0.5 =0.256
d.
Real Lorenzo curve
https://www.ons.gov.uk/peoplepopulationandcommunity/personalandhouseholdfinances/
incomeandwealth/compendium/wealthingreatbritainwave4/2012to2014/
chapter2totalwealthwealthingreatbritain2012to2014
The curve referred to above illustrate inequality in Great Britain for 4 wealth components. The
data used was collected between the year 2012 and 2014. All the components were graphed and
the curves compared to the 45 degree line. The closer the curve is to the 45 degrees diagonal, the
lesser the inequality and vice versa. From the research, the highest inequality was recorded in net
financial wealth. On the contrary, physical wealth showed more equality.
References
Rogawsky, J., & Adams, C. (2015). Calculus: Early Transcendentals (3rd ed.). W. H. Freeman.
Stewart, J. (2016). Calculus (8th ed.). Boston: Cengage Learning.
Stroud, K., & Dexter, B. (2013). Engineering Mathematics 7th Edition. Palgrave.