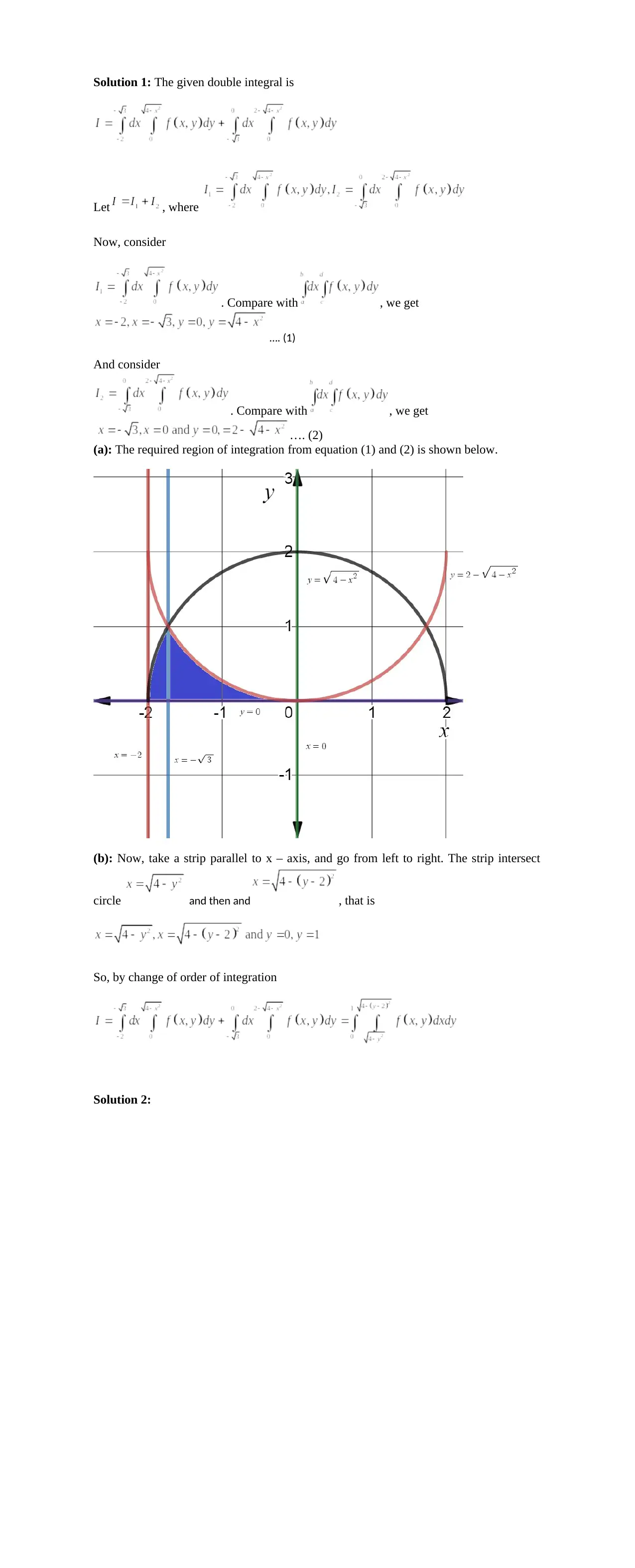
MAT2100 Assignment 2: Double Integrals, Work, and Vector Calculus

This document provides comprehensive solutions to MAT2100 Assignment 2, addressing a variety of calculus and vector analysis problems. The solutions begin with a double integral problem, involving sketching the region of integration and rewriting the integral with a reversed order of integration. The assignment then explores a force calculation problem on a rectangular plate where pressure is proportional to the square of the distance from a corner. Further solutions include calculating the work done by a force along a given path, proving the conservative nature of a force field and determining a potential function, and solving a second-order differential equation describing a spring system with friction, including finding both the general and particular solutions. Other solutions involve applying Green's theorem to calculate the area of a circle, analyzing vector properties such as length and orthogonality, determining the linear dependence of vectors using determinants, and finding eigenvalues and eigenvectors of a matrix. The solutions provide detailed step-by-step explanations, making it a valuable resource for students studying calculus and related topics.

Solution 1: The given double integral is
Let , where
Now, consider
. Compare with , we get
…. (1)
And consider
. Compare with , we get
…. (2)
(a): The required region of integration from equation (1) and (2) is shown below.
(b): Now, take a strip parallel to x – axis, and go from left to right. The strip intersect
circle and then and , that is
So, by change of order of integration
Solution 2:

Let be any point on the plate. Since the pressure (force per unit area) at any point
on the plate is proportional to the square of the distance of that point from one corner.
That is
The total force F is
Solution 3: Given the force function
, and
This implies that
So,
And
The work done is
So, wok done is

Solution 4: Given that . Compare with P we get
Now,
, and .
Since, , this implies that the function F is a conservative force. Then there exist
a potential function such that
This implies that
Comparing both sides we get
Integrating equation (1) we get
Differentiate equation (3) with respect to y partially we get
Using equation (2) we get
Use g(y) in equation (3), the potential function is
Now, the work done is

Solution 5: Given the motion of the spring system with friction is described by the
differential equation
a): The characteristic equation is . Solving we get
. When , we get
, double roots. Then the general solution is
, where a and b are constant
b): Given that and .
Now,
Since, . Then the required particular solution is
Solution 6: Given differential equation is
The characteristic equation is
Simplify we get
Then the complementary solution is . Now, the particular solution is
Then the general solution is

Since,
Since,
Solving equation (1) and (2) we get
Then the required particular solution is
Solution 7: Suppose that the equation of circle be . Suppose that the
boundary of the circle of radius r be D, that is . Now, the parametric equation
of circle is . By Green’s theorem, the area of the region is
Here and where
So,
Solution 8: Given vectors are .
a):
Length of vector v is
b):
Since , so a and b are orthogonal and so a and c are also orthogonal.
Solution 9: Given vectors . Note that the
vectors are linearly independent if and only if the determinant of associated matrix is non
zero, otherwise they are linearly dependent.
Now, the determinant of the associated matrix is
Since, the determinant is zero, the vectors
are linearly dependent. This completes
the proof.
Solution 10: The given matrix is
a):

Suppose that the eigenvalue be , and then the characteristic equation is
, that is
Solving we get
b):
Here the lowest eigenvalue is , so to find eigenvalue corresponding to eigenvalue
, we need to solve
The augmented matrix is
By elementary row operations we get
By backward substitution we get
. Let , we get
Hence, eigenvector corresponding to the eigenvalue is .