Calculus 1 (MATH 1063) Problem Solving Exercise 1, SP2, 2020

This document provides a detailed solution to a Calculus 1 (MATH 1063) problem-solving exercise. The solution covers a range of calculus concepts, including limits, continuity, and derivatives. The document demonstrates the application of the limit definition to find derivatives, and it also addresses the product and quotient rules for differentiation. Furthermore, it explores tangent lines and the area under a curve, integrating these concepts with problem-solving techniques. Finally, the solution includes analysis of functions, including their domains, and provides a step-by-step breakdown of each problem, making it a valuable resource for students studying calculus.

QUESTION ONE
(a) From the given graphical plot of the function f ( x )= x+1
x2−1 ,
The limit as x approaches 1 from the right is +∞ i.e. lim
x→ 1+¿
[ x+1
x2−1 ]=+∞ ¿
¿
Whereas
The limit as x approaches 1 from the right is −∞ i.e. lim
x→ 1−¿
[ x +1
x2−1 ] =−∞ ¿
¿
Since
lim
x→ 1+¿
[ x+1
x2−1 ] ≠ lim
x→1− ¿
[ x+ 1
x2
−1 ] ¿
¿¿
¿
, the limit does not exist
(b)
lim
x→−1 [ x +1
x2 −1 ] = lim
x →−1 [ x +1
(x−1)( x+1) ]
¿ lim
x→−1 [ 1
x−1 ]
¿ 1
−1−1 =−1
2
∴ lim
x →−1 [ x+ 1
x2−1 ]=−1
2
(c) For f ( x) to be continuous at x=−1 :
i) f ( x) must be defined at x=−1 ; however, f (−1) is undefined at x=−1
ii) The limit must exist i.e.
lim
x→−1 [ x +1
x2 −1 ]=−1
2 as shown in part (b). Thus the limit exists
iii) lim
x→−1
f ( x )=f (−1 ) ; however, lim
x→−1 [ x +1
x2 −1 ]≠ f (−1 ) as the function is not defined at
x=−1
∴ Since not all thecontinuity conditions have been met , the function is discontinous at

x=−1 . However , thediscontinuity is a removable one .
QUESTION TWO
From the definition of differentiation, d
dx f ( x ) =lim
h →0
f ( x+h ) −f ( x)
h
d
dx [−2 x2 +3 x +58 ]=lim
h →0
[−2 ( x +h )2 +3( x +h)+58 ] − [−2 x2 +3 x+58 ]
h
Expanding the numerator,
d
dx f ( x ) =lim
h →0
[ −2( x2+2 hx +h2 )+ 3 x +3 h+58 ] − [ −2 x2 +3 x +58 ]
h
¿ lim
h→ 0
[−2 x2−4 hx−2 h2 ¿+ 3 x +3 h+58 ]− [−2 x2 +3 x +58 ]
h
¿ lim
h→ 0
[ −2 x2+2 x2+ 3 x −3 x−4 hx −2h2+3 h+58−58 ]
h
¿ lim
h→ 0
[−4 hx−2 h2 +3 h ]
h
¿ lim
h→ 0
h [−2 h−4 x+3 ]
h
¿ lim
h→ 0
[−2 h−4 x +3 ]
¿−2 ( 0 )−4 x+ 3=−4 x +3
∴ d
dx [−2 x2 +3 x+58 ]=−4 x+3

QUESTION THREE
(a) Given p ( x ) = ( 2 x2 +3 x +1 ) ( x3 −x−1 ),
By Product rule i.e.
p' ( x )= [u ( x ) . v ( x ) ]'
=u' ( x ) . v ( x )+ u ( x ) . v' ( x )
For u ( x )= ( 2 x2+3 x +1 )∧v ( x ) = ( x3−x−1 )
p' ( x ) = ( x3 −x−1 ) ∙ d
dx [ 2 x2 +3 x +1 ] + ( 2 x2 +3 x+ 1 ) d
dx [ x3−x−1 ]
Applying power rule,
p' ( x )= ( x3 −x−1 ) ( 4 x +3 ) + ( 2 x2+ 3 x +1 ) (3 x2−1)
(b) Given q ( x )= 2 x2 +3 x +1
x3−x−1
Applying the quotient rule i.e.
q' ( x ) = [ u( x )
v( x) ]
'
=u' ( x ) . v ( x ) −u ( x ) . v ' ( x)
v ( x)2
For u ( x )= ( 2 x2+3 x +1 )∧v ( x ) = ( x3−x−1 )
q' ( x ) =
( x3−x−1 ) . d
dx [ 2 x2+ 3 x +1 ] − ( 2 x2 +3 x+1 ) d
dx [ x3−x−1 ]
( x3−x−1 ) 2

¿ ( x3 −x−1 ) ( 4 x +3 ) − ( 2 x2 +3 x+ 1 ) (3 x2−1)
( x3−x−1 )
2
∴ q' ( x )= ( x3 −x−1 ) ( 4 x +3 ) − ( 2 x2 +3 x+1 ) (3 x2 −1)
( x3−x−1 )2
(c) Given f ( x )=cos ( ax ) sin (ax ),where a is constant
By Product rule i.e.
f ' ( x ) = [ u ( x ) . v ( x ) ] '
=u' ( x ) . v ( x ) +u ( x ) . v' ( x )
For u ( x )=cos (ax )∧v ( x )=sin(ax) ,
f ' ( x )=sin (ax)∙ d
dx [ cos ( ax ) ]+ cos ( ax ) ∙ d
dx [ sin( ax) ]
¿ sin ( ax ) ∙−a sin ( ax ) +cos ( ax ) ∙ a cos (ax)
¿ a cos2 (ax )−a sin2 (ax)
∴ f ' ( x )=a [ cos2 ( ax ) −sin2 ( ax ) ]
(d) Given h ( x ) = tan ( √ x )
cos x
Applying the quotient rule,
h' ( x )=
[ u(x )
v (x ) ]'
= u' ( x ) . v ( x )−u ( x ) . v '( x )
v ( x)2
For u ( x ) =tan( √ x)∧v ( x ) =cos x

h' ( x ) =
cos x . d
dx [ tan( √ x ) ] − ( tan( √ x) ) d
dx [ cos x ]
cos2 ( x)
Recognizing that [ tan ( u ( x ) ) ]'
=sec2 (u ( x ) )∙ u '( x )∧ [ cos (x) ]'
=−sin( x)
h' ( x ) =sec2 ( √ x) ∙ cos x . d
dx [ √ x ] − ( tan ( √ x ) ) ¿ ¿
h' ( x )=sec2 (√ x) ∙ cos x . 1
2 x
1
2 −1
+ ( tan ( √x ) ) ¿ ¿
h' ( x )=sec2 (√ x) ∙ cos x . x
−1
2
2 + ( tan ( √x ) ) ¿ ¿
h' ( x )= sec2 (√ x)∙ cos x
2 √ x + ( tan ( √x ) ) ¿ ¿
∴ h' ( x ) = sec2 (√ x)
2 √ x ∙cos (x) + ( tan ( √ x ) ) ¿ ¿

QUESTION FOUR
(a) Two conditions must be met:
i) Common point of intersection of parabola and tangent:
2 x−1=x2
x2−2 x+1=0
( x−1 ) 2=0 Factorize
x=1
y=2 x−1=x2 =1
∴ ( 1,1 ) is the point that the tangent touchesthe parabola
ii) Gradient of the curve at point (1,1) should be equal to that of the tangent line
Gradient function of the parabola , dy
dx =2 x=2 ( 1 ) =2
Gradient of the tangent line=2
∴ 2= y−1
x−1 ; y =2 x−1 {confirms the equation of thetangent }
(b) ( 3,5 ) =(x , y )
y=2 x−1=2 ( 3 )−1=6−1=5
The value of x=3, gives y=5 based on the model y=2 x−1. Hence the line passes
through point (3,5)

(c) Gradient function, dy
dx =2 x
⇒ gradient of theline at the point of ∩withthe curve y=x2
Let (x , y ) be the point of intersection between the tangent line and the curve,
( x , x2 ) ∧ ( 3,5 ) are points on the tangent line whose gradient is 2 x
But m= y−5
x −3
2 x= x2−5
x−3
Simplifying,
2 x ( x−3 )=x2−5
x2−6 x +5=0
Factorizing ( x−1 ) ( x−5 )=0 ; x =1∨x=5
Valid x = 5
Gradient = 10
10= y −5
x−3 ; y−5=10 x−30
y=10 x−25
∴ Equationof the line is: y =10 x−25
Co−ordinate of the point wheretouches is :(5 , 25)

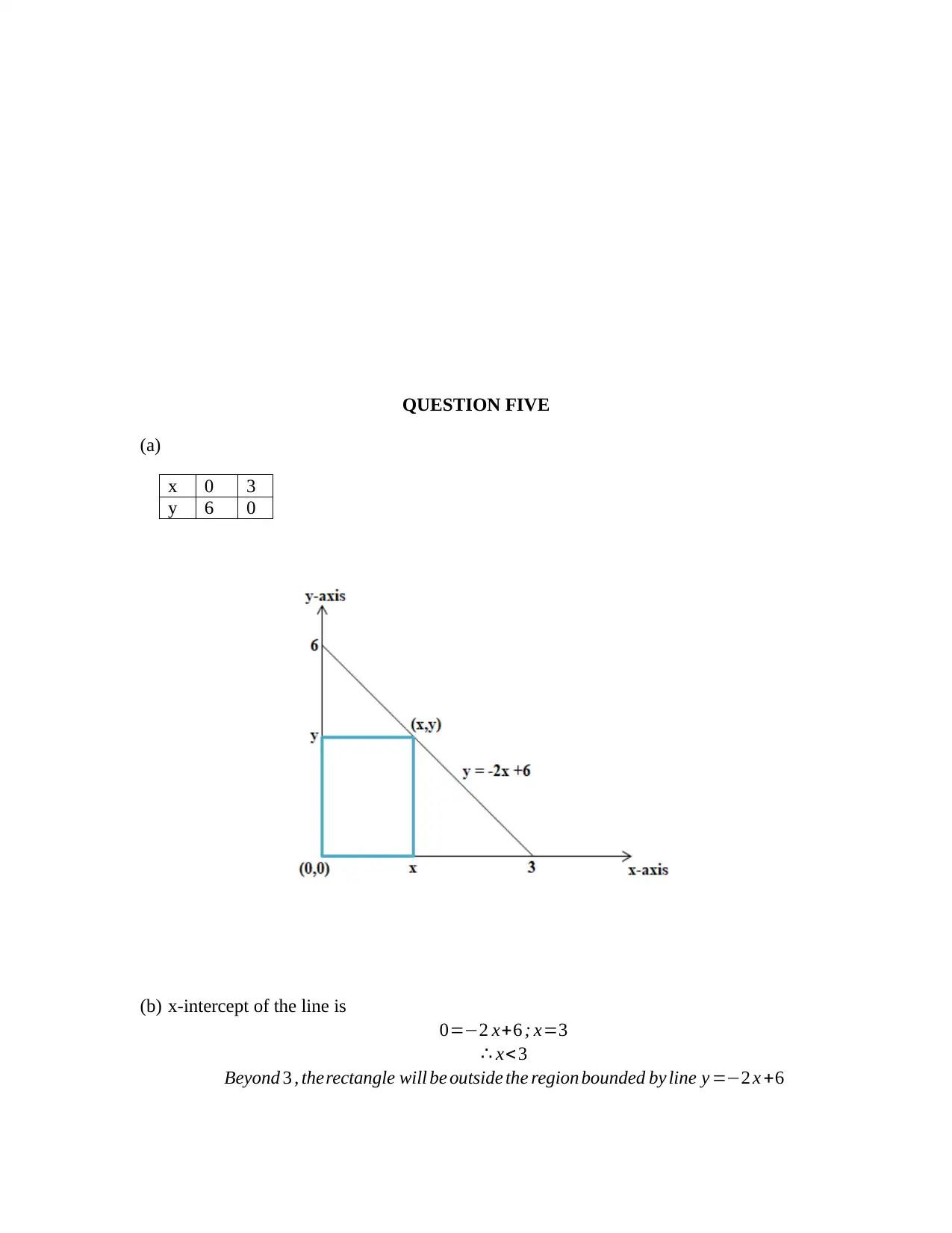
QUESTION FIVE
(a)
x 0 3
y 6 0
(b) x-intercept of the line is
0=−2 x+6 ; x=3
∴ x<3
Beyond 3 , therectangle will be outside the region bounded by line y =−2 x +6

(c)
Area=Length x Width
Length= y=−2 x +6
Width=x
∴ Area= ( −2 x +6 ) x=2 x ( 3−x ) square units
(d)
d
dx ( Area )=0 ,¿ get the valueof x for the largest area
d
dx ( Area )=2 ( 3−x )+2 x (−1 ) product rule
¿ 6−2 x −2 x=0
x= 6
4 =3
2
y=−2 (3
2 )+6=3
Largest area is thus,
¿ 3 × 3
2 =4.5 square units

QUESTION 6
a)
f can validly operate on all real values of x except at x = 1
Domain : [ Solution : x <1∨x >1
Interval notation : (−∞ , 1 ) ∪ ( 1 , ∞ ) ]Range : [ Solution : f ( x )< 0∨f (x)> 0
Interval notation :(−∞ , 0)∪ (0 , ∞) ]
b)
f ( x ) = 1
1−x = ( 1−x ) −1Let u=1−x du
dx =−1f =u−1 ; df
du =−u−2By chain rule ,
f ' ( x )= df
du × du
dx = (−1 ) (−u−2 ) =u−2 ¿ 1
( 1−x ) 2
c)
g(x) can validly operate on all real values of x except at x = 0
Domain : [ Solution : x <0∨x >0
Interval notation : (−∞, 0 ) ∪ ( 0 , ∞ ) ]Range : [ Solution : f ( x ) <1∨f ( x ) >1
Interval notation : (−∞ ,1 ) ∪ ( 1 , ∞ ) ]
d)
g ( x ) =1− 1
x ¿ 1−x−1 g' ( x ) =0− ( −x−2 )=x−2¿ 1
x2
e)
f ( g ( x ) ) = 1
1−g ( x ) where g ( x ) =1− 1
x Expressing g(x) as a single fraction, f ( g ( x ) ) reduces
to,

¿ 1
1−( x−1
x )
Multiplying each term by x, we get
x
x−(x−1)= x
x−x+1 =x
f)
From the domains of f(x) and g(x) found above, the value of x for which g(x) = 1 does
not exist.
∴ Domain of f ( g ( x ) ) is all real number s except at x=0
g)
fog ( x )= 1
1−g ( x ) = ( 1−g ( x ) )−1
where g ( x ) =1− 1
x Let u=1−g ( x ) so that fog ( x ) =u−1
du
dx =0−g' ( x ) =−g' ( x )
d
du ( fog ( x ) ) =−u−2=−1
u2
By chain rule,
d
dx ( fog ( x ) )= d
du ( fog ( x ) ) × du
dx … chainrule ¿ g' ( x )
u2
g' ( x ) = 1
x2 { ¿ part d } u=1−g ( x ) =1− ( 1− 1
x )= 1
x u2= ( 1
x )2
= 1
x2
d
dx ( fog ( x ) ) = g' ( x )
u2 = 1
x2 ÷ 1
x2 =1
( fog ( x ) ) '=1