MATH 107 Assignment 2 - Functions, Graphs, and Equations Problems
VerifiedAdded on 2022/10/04
|9
|683
|18
Homework Assignment
AI Summary
This document presents a complete solution for MATH 107 Assignment 2, addressing various mathematical concepts. The assignment covers topics such as finding the midpoint and radius of a circle, identifying functions from graphs, determining the domain and range of functions, finding x and y intercepts, working with function operations, and analyzing revenue and profit functions. Specific problems involve evaluating functions, simplifying expressions, and interpreting results within the context of cost, revenue, and profit scenarios. The solution includes detailed steps and explanations to aid in understanding the problem-solving process. The assignment also covers topics such as finding the domain of a function, calculating function values, simplifying expressions, and analyzing the symmetry of graphs.

Running head: MATH 107 ASSIGNMENT 1
MATH 107 Assignment
Firstname Lastname
Name of Institution
MATH 107 Assignment
Firstname Lastname
Name of Institution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
MATH 107 ASSIGNMENT 2
MATH 107
1. Consider the points (5, –2) and (–1, 4).
(a) State the midpoint)
Solution
midpoint= ( x1 + x2
2 , y1 + y2
2 ) =( 5+ ( −1 )
2 , −2+ 4
2 ) = ( 2 ,1 )
(b), find the length of the radius of the circle.
Solution
Length of the ˚¿ Magnitude ¿ point ( 2,1 ) ∧ ( 5 ,−2 )
¿ √ ( 5−2 )2 + ( 1−−2 )2
¿ √32 +32
¿ √ 18
¿ √ 9 x 2
3 √ 2units
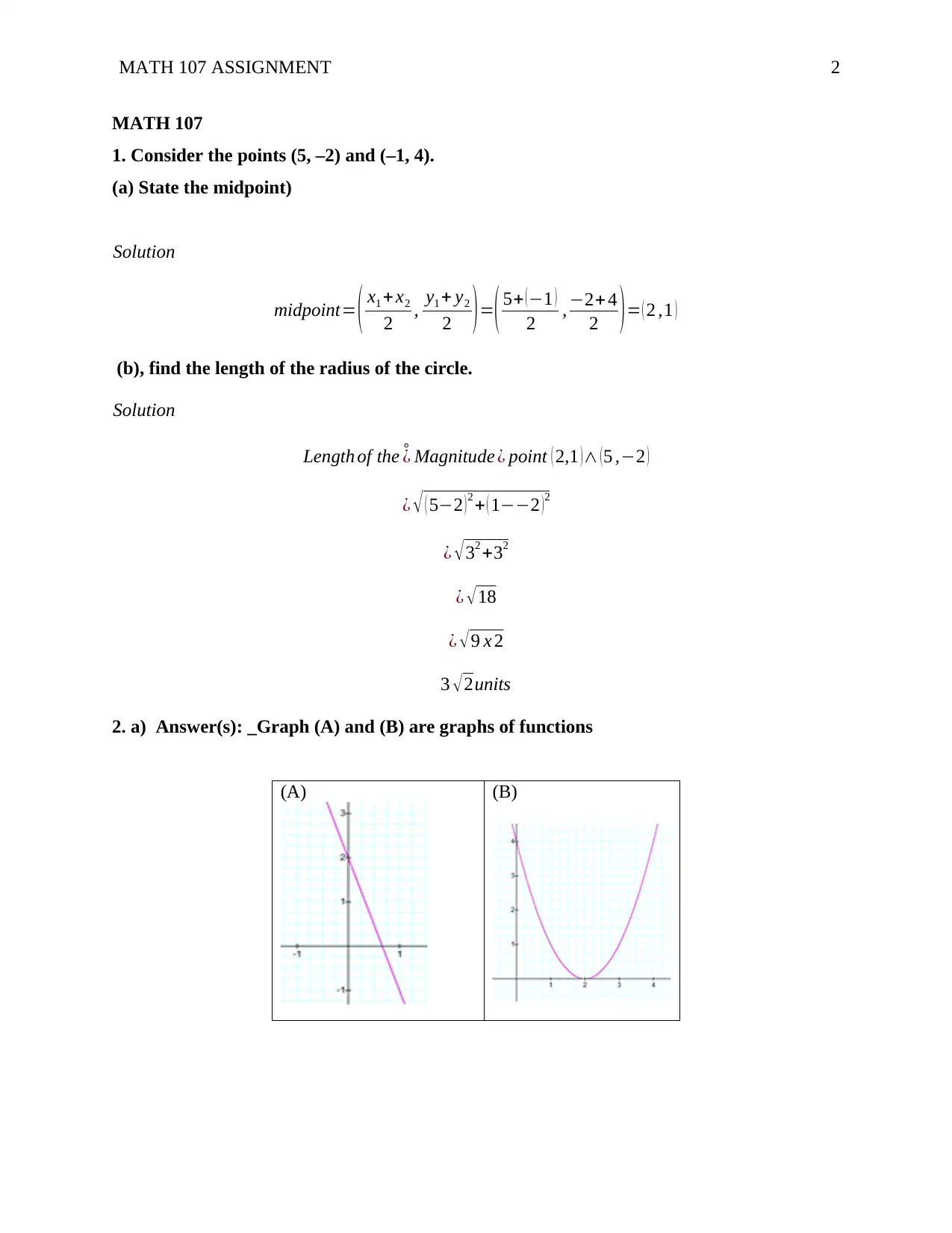
2. a) Answer(s): _Graph (A) and (B) are graphs of functions
(A) (B)
MATH 107
1. Consider the points (5, –2) and (–1, 4).
(a) State the midpoint)
Solution
midpoint= ( x1 + x2
2 , y1 + y2
2 ) =( 5+ ( −1 )
2 , −2+ 4
2 ) = ( 2 ,1 )
(b), find the length of the radius of the circle.
Solution
Length of the ˚¿ Magnitude ¿ point ( 2,1 ) ∧ ( 5 ,−2 )
¿ √ ( 5−2 )2 + ( 1−−2 )2
¿ √32 +32
¿ √ 18
¿ √ 9 x 2
3 √ 2units
2. a) Answer(s): _Graph (A) and (B) are graphs of functions
(A) (B)

MATH 107 ASSIGNMENT 3
b) If one imposes additional conditions, they all can become functions.
conditions
Vertical line test thus a function has only one output value for each input value
3. Consider the following graph of y = f (x).
(a) State the domain.
all x−values
domain ∈ [−1 , 6 ]
(b) State the range.
All y −values
Range ∈ [ −3 , 2 ]
(c) State the x-intercept(s).
x=−1
x=1
x=5
(d) State the y-intercept(s).
y=−3
4. Let f ( x ) = x +5
( x−2 ) 2
(a) State the domain of the function f ( x ) = x +5
( x−2 ) 2
Solution
f ( x )= x +5
x2−4 x+ 4
the domains are(−∞ ,2)∪ (2 , ∞)
(b) Calculate f ( −3 ). (work optional)
f ( −3 ) = −3+ 5
( −3−2 ) 2 = 2
25 =0.08
b) If one imposes additional conditions, they all can become functions.
conditions
Vertical line test thus a function has only one output value for each input value
3. Consider the following graph of y = f (x).
(a) State the domain.
all x−values
domain ∈ [−1 , 6 ]
(b) State the range.
All y −values
Range ∈ [ −3 , 2 ]
(c) State the x-intercept(s).
x=−1
x=1
x=5
(d) State the y-intercept(s).
y=−3
4. Let f ( x ) = x +5
( x−2 ) 2
(a) State the domain of the function f ( x ) = x +5
( x−2 ) 2
Solution
f ( x )= x +5
x2−4 x+ 4
the domains are(−∞ ,2)∪ (2 , ∞)
(b) Calculate f ( −3 ). (work optional)
f ( −3 ) = −3+ 5
( −3−2 ) 2 = 2
25 =0.08
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

MATH 107 ASSIGNMENT 4
(c) Find f ( a+2 ) and simplify as much as possible. Show work.
Solution
f ( x )= x+5
( x−2 )2
f ( x )= x +5
x2−4 x+ 4
thus for f ( a+2 ) = a+2+5
( a+ 2 ) 2−4 ( a+2 ) + 4
¿ a+7
a2 +4 a+4−4 a−8+4
¿ a+7
a2
6. Given f ( x ) =x −5 and g ( x )=|x +7|, which of the following is the domain of the quotient
function f /g ?
solution
f ( x )=x −5∧g ( x )
f ( x )
g ( x ) = x−5
x+7
the function is defined only when x+7 ≠ 0
thus x ≠−7
thus domain= (−∞ ,−7 ) ∪ (−7 , ∞ )
7. For income x (in dollars), a particular state's income tax T (in dollars) is given by
T ( x )= { 0.025 x if 0 ≤ x ≤ 3000
75+0.042( x−3000) if 3000<x ≤ 6000
201+0.055( x −6000) if x >6000
(a) What is the tax on an income of $5,100? Show some work.
(c) Find f ( a+2 ) and simplify as much as possible. Show work.
Solution
f ( x )= x+5
( x−2 )2
f ( x )= x +5
x2−4 x+ 4
thus for f ( a+2 ) = a+2+5
( a+ 2 ) 2−4 ( a+2 ) + 4
¿ a+7
a2 +4 a+4−4 a−8+4
¿ a+7
a2
6. Given f ( x ) =x −5 and g ( x )=|x +7|, which of the following is the domain of the quotient
function f /g ?
solution
f ( x )=x −5∧g ( x )
f ( x )
g ( x ) = x−5
x+7
the function is defined only when x+7 ≠ 0
thus x ≠−7
thus domain= (−∞ ,−7 ) ∪ (−7 , ∞ )
7. For income x (in dollars), a particular state's income tax T (in dollars) is given by
T ( x )= { 0.025 x if 0 ≤ x ≤ 3000
75+0.042( x−3000) if 3000<x ≤ 6000
201+0.055( x −6000) if x >6000
(a) What is the tax on an income of $5,100? Show some work.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MATH 107 ASSIGNMENT 5
Solution
T ( x ) =75+ 0.042 ( x−3000 )
T (5100)=75+0.042 ( 5100−3000 )
¿ 75+88.20
T (5100)=$ 163.20
(b) What is the tax on an income of $51,000? Show some work.
Solution
T ( x ) =201+0.055 ( x−6000 )
T (51000)=201+0.055 ( 51000−6000 )
201+2475
T (51000)=$ 2676
8. Let y = 2 2(x-1)2.
(a) Find the x-intercept(s) of the graph of the equation, if any exist.
Solution
y=2−2 ( x −1 ) 2
y=2−2 ( x2 −2 x +1 )
y=−2 x2 +4 x
at x −intercept , y =0 , thus−2 x2 + 4 x
therefore solution of the equation , x=0∧2
hence x −intercept=0∧2
(b) Find the y-intercept(s) of the graph of the equation, if any exist. (work optional)
solution
Solution
T ( x ) =75+ 0.042 ( x−3000 )
T (5100)=75+0.042 ( 5100−3000 )
¿ 75+88.20
T (5100)=$ 163.20
(b) What is the tax on an income of $51,000? Show some work.
Solution
T ( x ) =201+0.055 ( x−6000 )
T (51000)=201+0.055 ( 51000−6000 )
201+2475
T (51000)=$ 2676
8. Let y = 2 2(x-1)2.
(a) Find the x-intercept(s) of the graph of the equation, if any exist.
Solution
y=2−2 ( x −1 ) 2
y=2−2 ( x2 −2 x +1 )
y=−2 x2 +4 x
at x −intercept , y =0 , thus−2 x2 + 4 x
therefore solution of the equation , x=0∧2
hence x −intercept=0∧2
(b) Find the y-intercept(s) of the graph of the equation, if any exist. (work optional)
solution
MATH 107 ASSIGNMENT 6
y−intercept is at where x=0¿ the equation
y=−2 x2 +4 x we have
y=¿
y−intercept =0
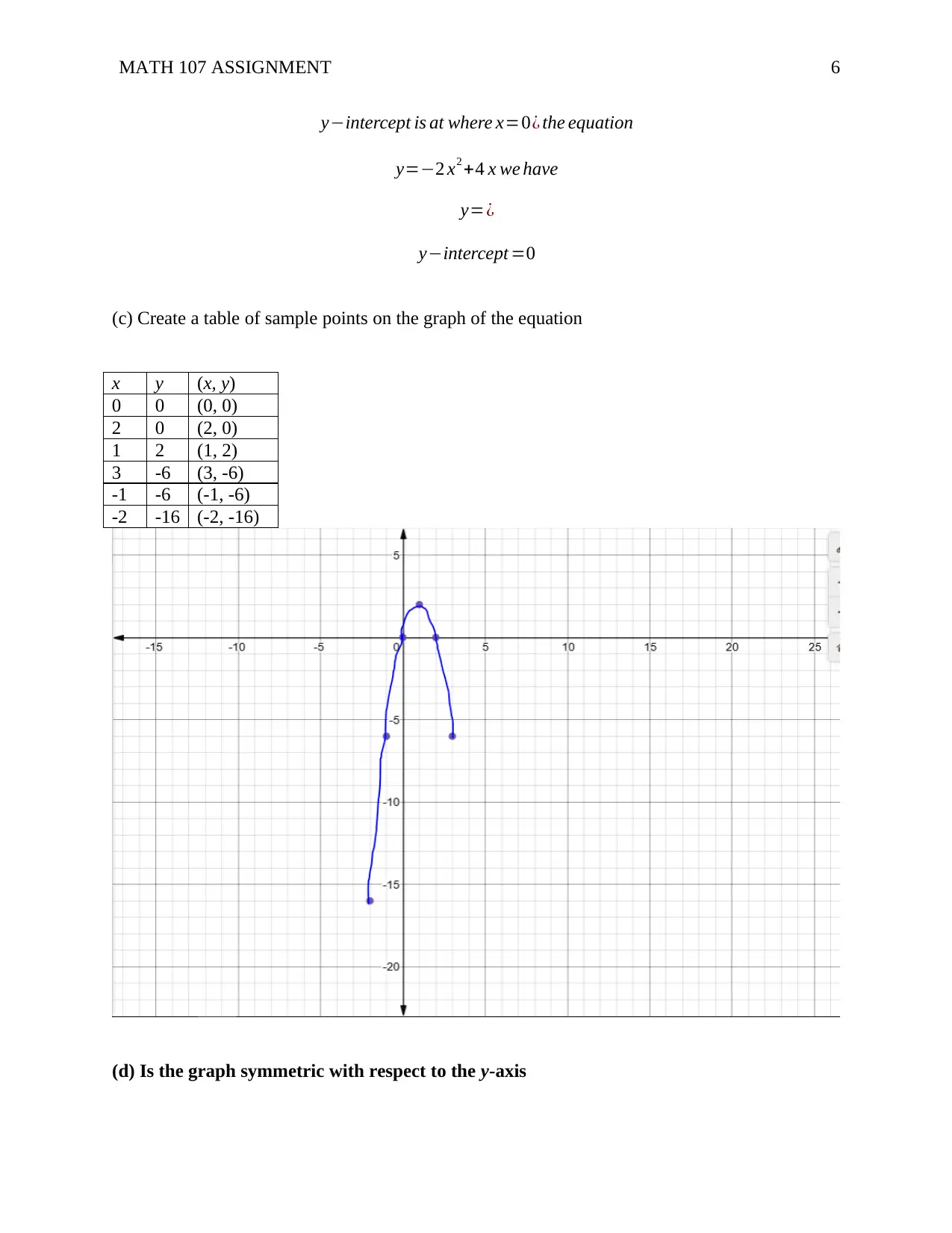
(c) Create a table of sample points on the graph of the equation
(d) Is the graph symmetric with respect to the y-axis
x y (x, y)
0 0 (0, 0)
2 0 (2, 0)
1 2 (1, 2)
3 -6 (3, -6)
-1 -6 (-1, -6)
-2 -16 (-2, -16)
y−intercept is at where x=0¿ the equation
y=−2 x2 +4 x we have
y=¿
y−intercept =0
(c) Create a table of sample points on the graph of the equation
(d) Is the graph symmetric with respect to the y-axis
x y (x, y)
0 0 (0, 0)
2 0 (2, 0)
1 2 (1, 2)
3 -6 (3, -6)
-1 -6 (-1, -6)
-2 -16 (-2, -16)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

MATH 107 ASSIGNMENT 7
No .let point ( 1 , 2 ) , reflection across y−axisbe ( 0 ,2 )
(e) Is the graph symmetric with respect to the x-axis
No .let point ( 1 , 2 ) , reflection across x−axis gives (−2, 0 )
(f) Is the graph symmetric with respect to the origin
No .the equation is a function of x∧ y values
9. Let f (x) = 3x2 + 3x – 8 and g(x) = 1 – 2x.
(a) Evaluate the function g – f for x = –1. That is, find (g – f)(–1). Show work.
Solution
g−f =g ( x )−f ( x )=1−2 x−3 x2−3 x+ 8
¿−3 x2 −5 x +9
( g−f ) (−1 )=−3 (−1 )2 −5 (−1 )+9
¿ 11
(b) Evaluate the function fg for x = –2. That is, find (f g) (–2). Show work.
Solution
fg= ( 3 x2+3 x−8 ) (1−2 x )
¿ 3 x2+3 x−8−6 x3−6 x2 +16 x
thus fg=−6 x3 −3 x2 +19 x−8
for fg (−2 )=−6 (−2 )3−3 (−2 )2 + ( 19 (−2 ) )−8
¿−10
(c) Find the difference function (f – g)(x) and simplify the results. Show work.
solution
( f −g ) ( x ) =3 x2+3 x−8− ( 1−2 x )
¿ 3 x2+3 x−8−1+2 x
( f −g ) ( x ) =3 x2+5 x−9
No .let point ( 1 , 2 ) , reflection across y−axisbe ( 0 ,2 )
(e) Is the graph symmetric with respect to the x-axis
No .let point ( 1 , 2 ) , reflection across x−axis gives (−2, 0 )
(f) Is the graph symmetric with respect to the origin
No .the equation is a function of x∧ y values
9. Let f (x) = 3x2 + 3x – 8 and g(x) = 1 – 2x.
(a) Evaluate the function g – f for x = –1. That is, find (g – f)(–1). Show work.
Solution
g−f =g ( x )−f ( x )=1−2 x−3 x2−3 x+ 8
¿−3 x2 −5 x +9
( g−f ) (−1 )=−3 (−1 )2 −5 (−1 )+9
¿ 11
(b) Evaluate the function fg for x = –2. That is, find (f g) (–2). Show work.
Solution
fg= ( 3 x2+3 x−8 ) (1−2 x )
¿ 3 x2+3 x−8−6 x3−6 x2 +16 x
thus fg=−6 x3 −3 x2 +19 x−8
for fg (−2 )=−6 (−2 )3−3 (−2 )2 + ( 19 (−2 ) )−8
¿−10
(c) Find the difference function (f – g)(x) and simplify the results. Show work.
solution
( f −g ) ( x ) =3 x2+3 x−8− ( 1−2 x )
¿ 3 x2+3 x−8−1+2 x
( f −g ) ( x ) =3 x2+5 x−9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MATH 107 ASSIGNMENT 8
10. The cost to produce x widgets is given by C(x) = 5250 + 7.00x for
x 0, and the price-demand function, in dollars per widget, is p(x) = 45 0.02x for 0 x
2250.
(a) Find and interpret C(300).
Solution
¿ find C ( 300 ) , we the|cost function for producing 300 widgets
C (300)=5250+7(300)=7350
Therefore ,costs $ 7350 ¿ produce 300 widgets .
(b) Find and interpret C(300). (Note that C(x) is the average cost function.)
The average cost function is the ratio of thetotal cost function ¿ the quantity produced .
The function is defined as
C ( x ) = 5250+7 x
x
¿ 5250
x +7
By evaluating cost , we find the average cost per unit of producing that quantity .
C ( 300 )=5250
300 +7=24.5
Thus , the average cost per widget when300 widgets are produced are $ 24.50 per widget
(c) Find and simplify the expression for the revenue function R(x). (work optional)
Demand function is used ¿ find the function since revenue is defined as
the price per unit×the quantity sold
The expression is as follows
R=px
¿( 45−0.02 x )x
10. The cost to produce x widgets is given by C(x) = 5250 + 7.00x for
x 0, and the price-demand function, in dollars per widget, is p(x) = 45 0.02x for 0 x
2250.
(a) Find and interpret C(300).
Solution
¿ find C ( 300 ) , we the|cost function for producing 300 widgets
C (300)=5250+7(300)=7350
Therefore ,costs $ 7350 ¿ produce 300 widgets .
(b) Find and interpret C(300). (Note that C(x) is the average cost function.)
The average cost function is the ratio of thetotal cost function ¿ the quantity produced .
The function is defined as
C ( x ) = 5250+7 x
x
¿ 5250
x +7
By evaluating cost , we find the average cost per unit of producing that quantity .
C ( 300 )=5250
300 +7=24.5
Thus , the average cost per widget when300 widgets are produced are $ 24.50 per widget
(c) Find and simplify the expression for the revenue function R(x). (work optional)
Demand function is used ¿ find the function since revenue is defined as
the price per unit×the quantity sold
The expression is as follows
R=px
¿( 45−0.02 x )x

MATH 107 ASSIGNMENT 9
¿ 45 x−0.02 x2
(d) Find and simplify the expression for the profit function P(x). (work optional) Note that
p(x) and P(x) are different functions.
Soltuion
We can determine , this by taking the difference between the revenue∧cost functions .
P=R−C
¿(45 x−0.02 x2 )−(5250+7 x)
¿−0.02 x2 +38 x−5250
(e) Find and interpret P (300), where P(x) is the profit function in part (d).
Soltuion
P ( 300 ) =−0.02 ( 300 ) 2+38 ( 300 ) −5250=4350
Thus , when 300 widgets are sold , the company makes a profit of $ 4350.
¿ 45 x−0.02 x2
(d) Find and simplify the expression for the profit function P(x). (work optional) Note that
p(x) and P(x) are different functions.
Soltuion
We can determine , this by taking the difference between the revenue∧cost functions .
P=R−C
¿(45 x−0.02 x2 )−(5250+7 x)
¿−0.02 x2 +38 x−5250
(e) Find and interpret P (300), where P(x) is the profit function in part (d).
Soltuion
P ( 300 ) =−0.02 ( 300 ) 2+38 ( 300 ) −5250=4350
Thus , when 300 widgets are sold , the company makes a profit of $ 4350.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



