MATH 107 Midterm Exam Assignment Solution Fall 2019
VerifiedAdded on 2022/10/16
|10
|558
|448
Homework Assignment
AI Summary
This document presents a comprehensive solution to a MATH 107 midterm exam. The assignment covers a wide range of mathematical concepts including solving quadratic equations, calculating income tax, interpreting and analyzing graphs, working with linear equations, determining the cheapest purchase option, understanding coordinate transformations, finding the line of best fit, evaluating difference functions, and analyzing profit functions. The solution includes step-by-step explanations, calculations, and answers to all questions from the midterm exam, providing a detailed understanding of each concept. The document also references the provided textbook and other academic resources.

Running head: MATHS ASSIGNMENT 1
Maths Assignment
Firstname Lastname
Name of Institution
Maths Assignment
Firstname Lastname
Name of Institution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MATHS ASSIGNMENT 2
Question 1
Consider the equation ( x +5 ) ( x – 2 ) =18
a) Expressing the equation in the form of a x2 +bx+ c=0
x ( x−2 )+ 5 ( x−2 )=18
x2−2 x+5 x−10=18
x2+3 x −28=0
b) Solving the equation
The solution takes the form x=−b ± √b2−4 ac
2 a
x=−3 ± √9+112
2
x=4∧−7
Question 2
Calculating income tax for an income of 68000
68000 is above 20000 brackets therefore the formula to be used is
T ( x )=440+0.033 ( x−20,000 )
T ( 68000 ) =440+0.033 ( 68000−20000 )
income tax=2024
Question 1
Consider the equation ( x +5 ) ( x – 2 ) =18
a) Expressing the equation in the form of a x2 +bx+ c=0
x ( x−2 )+ 5 ( x−2 )=18
x2−2 x+5 x−10=18
x2+3 x −28=0
b) Solving the equation
The solution takes the form x=−b ± √b2−4 ac
2 a
x=−3 ± √9+112
2
x=4∧−7
Question 2
Calculating income tax for an income of 68000
68000 is above 20000 brackets therefore the formula to be used is
T ( x )=440+0.033 ( x−20,000 )
T ( 68000 ) =440+0.033 ( 68000−20000 )
income tax=2024

MATHS ASSIGNMENT 3
Question 3
(a) Which of these graphs (if any) is symmetric with respect to the x-axis? Answer(s):
__C_______
(b) Which of these graphs (if any) is symmetric with respect to the y-axis? Answer(s):
___D______
(c) Which of these graphs (if any) is symmetric with respect to origin? Answer(s): ___A______
(d) Which of these graphs (if any) represents a function? Answer(s): ____A, B and D__
Question 4
a) x−intercept =2∧−5
b) y−intercept =4
c) Domain=−6∧3
d) range=−2 ≤ y ≤ 4
e) f ( −2 ) =0
f) The function isincreasing ¿−6 ≤ x ≤−3
Question 5
a) State an equation that represents Apex Marketing 's total charge A for an order of
x mugs.
A=20+4.50 x
b) State an equation that represents Best Brands’ total charge B for an order of x
mugs
Question 3
(a) Which of these graphs (if any) is symmetric with respect to the x-axis? Answer(s):
__C_______
(b) Which of these graphs (if any) is symmetric with respect to the y-axis? Answer(s):
___D______
(c) Which of these graphs (if any) is symmetric with respect to origin? Answer(s): ___A______
(d) Which of these graphs (if any) represents a function? Answer(s): ____A, B and D__
Question 4
a) x−intercept =2∧−5
b) y−intercept =4
c) Domain=−6∧3
d) range=−2 ≤ y ≤ 4
e) f ( −2 ) =0
f) The function isincreasing ¿−6 ≤ x ≤−3
Question 5
a) State an equation that represents Apex Marketing 's total charge A for an order of
x mugs.
A=20+4.50 x
b) State an equation that represents Best Brands’ total charge B for an order of x
mugs
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

MATHS ASSIGNMENT 4
B=62+3.90 x
c) The cheapest company to purchase from
Cost of 120 mugs at Apex , A=20+(4.50 x 120)=560
cost of 120 mugs at Best brand , B=62+(3.90 x 120)=53 0
Best brand company is cheaper for 120 mugs
d) Total charge for mug same
this is found by equating the two equations
20+ 4.50 x =62+ 3.90 x
0.6 x=42
x=70 mugs
At 70 mugs, the price is equal
Question 6
The equation the graph represents
¿ the graph ,the line passes through points ( 0 ,2 ) , (−6,0 )
the gradient = 2−0
0−−6 = 2
6 = 1
3
the y−intercept =2
considering theequation∈the form of y =mx+c , we have
y= 1
3 x +2 answer ( choice A )
B=62+3.90 x
c) The cheapest company to purchase from
Cost of 120 mugs at Apex , A=20+(4.50 x 120)=560
cost of 120 mugs at Best brand , B=62+(3.90 x 120)=53 0
Best brand company is cheaper for 120 mugs
d) Total charge for mug same
this is found by equating the two equations
20+ 4.50 x =62+ 3.90 x
0.6 x=42
x=70 mugs
At 70 mugs, the price is equal
Question 6
The equation the graph represents
¿ the graph ,the line passes through points ( 0 ,2 ) , (−6,0 )
the gradient = 2−0
0−−6 = 2
6 = 1
3
the y−intercept =2
considering theequation∈the form of y =mx+c , we have
y= 1
3 x +2 answer ( choice A )
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
MATHS ASSIGNMENT 5
Question 7
Consider the points (-2, 5) and (1, -4)
a) The distance between the two points (Precup, 2013)
distance= √ ( 1−−2 ) 2+ ( −4−5 ) 2= √ 32 + ( −9 ) 2
¿ √ 90
¿ 3 √ 10
b) Slope= ∆ y
∆ x =−4−5
1−−2 =−9
3 =−3
c) Equation
y−5
x +2 =−3
y−5=−3 ( x +2 )
y=−3 x −6+5
y=−3 x −1
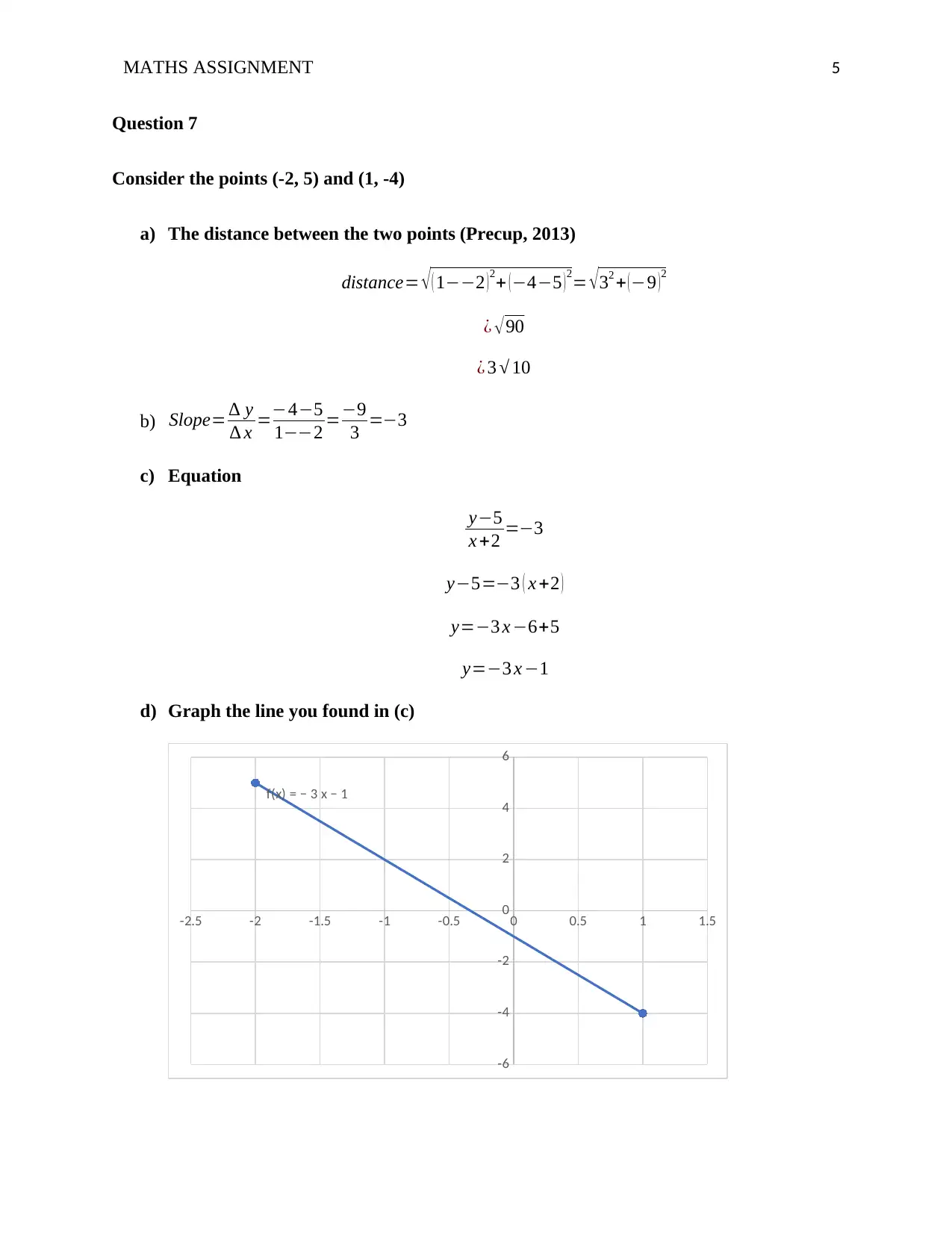
d) Graph the line you found in (c)
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5
-6
-4
-2
0
2
4
6
f(x) = − 3 x − 1
Question 7
Consider the points (-2, 5) and (1, -4)
a) The distance between the two points (Precup, 2013)
distance= √ ( 1−−2 ) 2+ ( −4−5 ) 2= √ 32 + ( −9 ) 2
¿ √ 90
¿ 3 √ 10
b) Slope= ∆ y
∆ x =−4−5
1−−2 =−9
3 =−3
c) Equation
y−5
x +2 =−3
y−5=−3 ( x +2 )
y=−3 x −6+5
y=−3 x −1
d) Graph the line you found in (c)
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5
-6
-4
-2
0
2
4
6
f(x) = − 3 x − 1
MATHS ASSIGNMENT 6
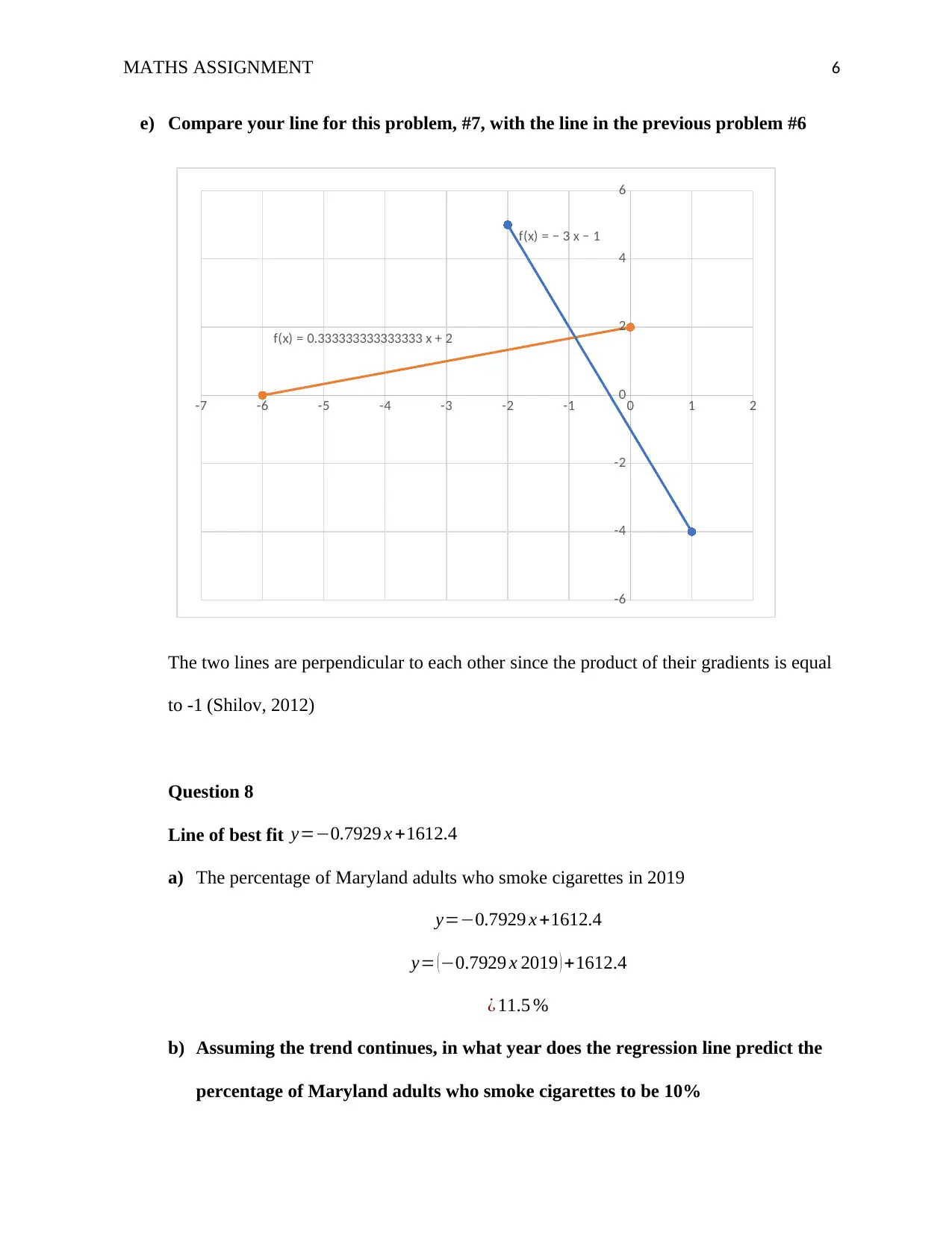
e) Compare your line for this problem, #7, with the line in the previous problem #6
-7 -6 -5 -4 -3 -2 -1 0 1 2
-6
-4
-2
0
2
4
6
f(x) = 0.333333333333333 x + 2
f(x) = − 3 x − 1
The two lines are perpendicular to each other since the product of their gradients is equal
to -1 (Shilov, 2012)
Question 8
Line of best fit y=−0.7929 x +1612.4
a) The percentage of Maryland adults who smoke cigarettes in 2019
y=−0.7929 x +1612.4
y= (−0.7929 x 2019 ) +1612.4
¿ 11.5 %
b) Assuming the trend continues, in what year does the regression line predict the
percentage of Maryland adults who smoke cigarettes to be 10%
e) Compare your line for this problem, #7, with the line in the previous problem #6
-7 -6 -5 -4 -3 -2 -1 0 1 2
-6
-4
-2
0
2
4
6
f(x) = 0.333333333333333 x + 2
f(x) = − 3 x − 1
The two lines are perpendicular to each other since the product of their gradients is equal
to -1 (Shilov, 2012)
Question 8
Line of best fit y=−0.7929 x +1612.4
a) The percentage of Maryland adults who smoke cigarettes in 2019
y=−0.7929 x +1612.4
y= (−0.7929 x 2019 ) +1612.4
¿ 11.5 %
b) Assuming the trend continues, in what year does the regression line predict the
percentage of Maryland adults who smoke cigarettes to be 10%
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
MATHS ASSIGNMENT 7
t he equation takes as follows , y =−0.7929 x+1612.4
substituting value of y , we have 10=−0.7929 x+ 1612.4
−1602.4=−0.7929 x
x=2020.93
thus the answer=2021
c) For each increase of one year, the percentage of Maryland adults who smoke
cigarettes decreases by 0.7929 %.
Question 9
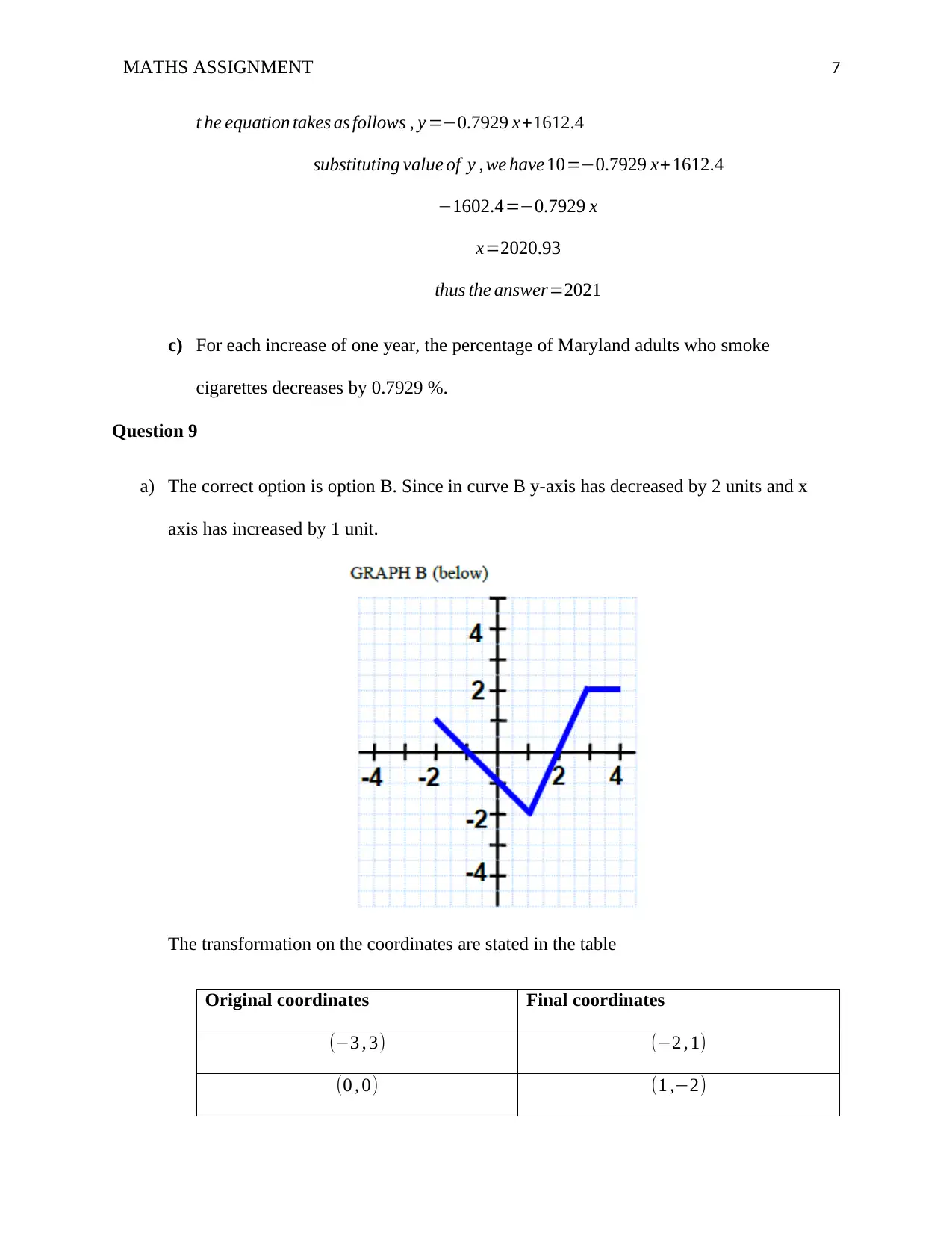
a) The correct option is option B. Since in curve B y-axis has decreased by 2 units and x
axis has increased by 1 unit.
The transformation on the coordinates are stated in the table
Original coordinates Final coordinates
(−3 , 3) (−2 , 1)
(0 , 0) (1 ,−2)
t he equation takes as follows , y =−0.7929 x+1612.4
substituting value of y , we have 10=−0.7929 x+ 1612.4
−1602.4=−0.7929 x
x=2020.93
thus the answer=2021
c) For each increase of one year, the percentage of Maryland adults who smoke
cigarettes decreases by 0.7929 %.
Question 9
a) The correct option is option B. Since in curve B y-axis has decreased by 2 units and x
axis has increased by 1 unit.
The transformation on the coordinates are stated in the table
Original coordinates Final coordinates
(−3 , 3) (−2 , 1)
(0 , 0) (1 ,−2)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MATHS ASSIGNMENT 8
(2 , 4) (3 , 2)
(3 , 4) (4 , 2)
Question 10
Let f (x)=6 x2 + √ x+ 7∧g (x)=4 x2−x +9
a) Find the difference function (f – g) (x) and simplify the results.
( f −g ) ( x )=f ( x )−g ( x )
¿ 6 x2+ √x +7+ 4 x2−x +9
f ( x )−g ( x )=10 x2 + √x +7−x+ 9
b) Evaluate the difference function f – g for x = –3. That is, find (f – g) (–3)
( f −g ) ( −3 ) =f ( −3 ) −g (−3 )
¿ 6 (−3 )2 + √−3+7−4 (−3 )2 + (−3 ) −9
¿ 8
c) Which of the following is the domain of the difference function f – g
−7 , ∞
Question 11
a) vertex : ( 1 , 4 )
b) State therange :(−∞ , 4 )
c) State the interval on which the function is decreasing:1< x <∞
d) The graph represents which of the following equations y=– x2+2 x +3
Question 12
The profit, in dollars, to produce and sell x widgets at XYZ is given b
(2 , 4) (3 , 2)
(3 , 4) (4 , 2)
Question 10
Let f (x)=6 x2 + √ x+ 7∧g (x)=4 x2−x +9
a) Find the difference function (f – g) (x) and simplify the results.
( f −g ) ( x )=f ( x )−g ( x )
¿ 6 x2+ √x +7+ 4 x2−x +9
f ( x )−g ( x )=10 x2 + √x +7−x+ 9
b) Evaluate the difference function f – g for x = –3. That is, find (f – g) (–3)
( f −g ) ( −3 ) =f ( −3 ) −g (−3 )
¿ 6 (−3 )2 + √−3+7−4 (−3 )2 + (−3 ) −9
¿ 8
c) Which of the following is the domain of the difference function f – g
−7 , ∞
Question 11
a) vertex : ( 1 , 4 )
b) State therange :(−∞ , 4 )
c) State the interval on which the function is decreasing:1< x <∞
d) The graph represents which of the following equations y=– x2+2 x +3
Question 12
The profit, in dollars, to produce and sell x widgets at XYZ is given b

MATHS ASSIGNMENT 9
P( x )=−0.02 x2+18 x−600 for x ≥ 0
a) vertex , x=−b
2 a
where a=−0.02 , b=18∧c=−600
x= −18
2∗−0.02=450
y=−0.02 x 4502 +18 x 450−600=3450
vertex= ( 450 , 3450 )
b) The maximum profit=$ 3450 when 450 widgets are produced
c) The number of widgets to be produced and sold in order to earn a profit of exactly $1,000
P ( x ) =−0.02 x2 +18 x−600
1000=−0.02 x2 +18 x−600
−0.02 x2+18 x−1600=0
x=−b ± √b2−4 ac
2 a =−18 ± √182− ( 4∗−0.02∗−1600 )
2∗−0.02
x= ( −18 ±14 )
−0.04 =100∨800
the number of widgets ¿ be produced∧sold for a profit of $ 1000
are 100 widgets∧800 widgets
P( x )=−0.02 x2+18 x−600 for x ≥ 0
a) vertex , x=−b
2 a
where a=−0.02 , b=18∧c=−600
x= −18
2∗−0.02=450
y=−0.02 x 4502 +18 x 450−600=3450
vertex= ( 450 , 3450 )
b) The maximum profit=$ 3450 when 450 widgets are produced
c) The number of widgets to be produced and sold in order to earn a profit of exactly $1,000
P ( x ) =−0.02 x2 +18 x−600
1000=−0.02 x2 +18 x−600
−0.02 x2+18 x−1600=0
x=−b ± √b2−4 ac
2 a =−18 ± √182− ( 4∗−0.02∗−1600 )
2∗−0.02
x= ( −18 ±14 )
−0.04 =100∨800
the number of widgets ¿ be produced∧sold for a profit of $ 1000
are 100 widgets∧800 widgets
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

MATHS ASSIGNMENT 10
References
Precup, R. (2013). Linear and semilinear partial differential equations. Berlin: De Gruyter.
Shilov, G. (2012). Linear Algebra. Newburyport: Dover Publications.
References
Precup, R. (2013). Linear and semilinear partial differential equations. Berlin: De Gruyter.
Shilov, G. (2012). Linear Algebra. Newburyport: Dover Publications.
1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

