MATH 115 Quiz 3 Summer 2018: Solving Equations and Applications

This document contains the solved solutions for a MATH 115 quiz from Summer 2018. The quiz covers a range of topics including solving exponential equations, calculating compound interest, determining radioactive decay rates and half-life, modeling population growth, simplifying logarithmic expressions, and solving logarithmic equations. Each problem provides a step-by-step solution, offering clarity on the methods used to arrive at the correct answer. The solutions demonstrate an understanding of algebraic manipulation, exponential and logarithmic functions, and their applications in various real-world scenarios. Desklib provides access to a wide range of solved assignments and past papers to help students excel in their studies.

MATH 115 Quiz 3 Summer 2018
1. Solve the following: 21−x=42 x
Solution: 21−x=42 x
⟹ 21−x= ( 22 )
2 x
⟹ 21−x=24 x
If base term is same then power will be equal.
Therefore, ⟹ 1−x=4 x
⟹ 1=5 x
⟹ x= 1
5
2. How long will it take an investment to double if it is invested at 7.8%, compounded
continuously?
Solution: Given r = 7.8 % = 7.8
100 = 0.078
if the interest rate is compounded continuously, then the general form is:
a=b ert
a → Amount after time ‘t’
b → Initial amount
r → Rate of interest compounded continuously
t → Time in years
Let, Initial amount = b
Amount after time ‘t’ = 2b (doubled)
Then equation looks like
⟹ 2 b=b e0.078 t
⟹ 2=e0.078 t
⟹ 0.078 t=ln 2

⟹ 0.078 t =0.693147
⟹ t= 0.693147
0.078
⟹ t=8.8865 Years
3. An initial investment of $1000 is appreciated for 2 years in an
account that earns 6% interest, compounded semiannually.
Find the amount of money in the account at the end of the
period.
Solution: Given
Initial investment P = $ 1000
Time ‘ t ‘ = 2 years
Rate of interest = r = 6 % = 0.06
Semiannually = N = 2
Let us suppose at the end of period, amount of money be A
Then A=P(1+ r
N )
t N
Where A=1000 (1+ 0.06
2 )2∗2
A=1000 ( 1+ 0.03 ) 4
A=1000 (1.03 )4
A=$ 1125.5
4. A company begins a radio advertising campaign in Chicago to
market a new soft drink. The percentage of the target market
that buys a soft drink is estimated by the function
Solution:
Given:
P ( t ) =100−100 e−0.01 t
Where P(t) is the percentage of the target market that buys soft drink.
“t” is the number of days of campaign.

Given, P ( t ) =75 %
⟹ 75=100−100 e−0.01t
⟹−25=−100 e−0.01 t
⟹ 1=4 e−0.01 t
⟹ 1
4 =e−0.01t
Take natural log both sides, ⟹ ln 1
4 =−0.01t
⟹ ln 0.25=−0.01t
⟹−1.38629=−0.01 t
t=138.63 days
5. A certain radioactive isotope decays at a rate of 0.15%
annually. Determine the half-life of this isotope, to the nearest
year.
Solution:
Radioactive isotope decay takes place exponentially
N=N 0 ekt (1)
Where N is the concentration of isotope left after time ‘t’
and No is the Initial concentration
k is the order of decay
Therefore,
Given , t = 1 year
Concentration of isotope left after 1year,
N=N 0−( 0.15 % of N0 )
N=N 0− 0.15
100 N0
N=N 0 (1−0.0015)

N=0.9985 N 0
Now plugging “N” and “t” value in the exponential equation (1)
N=N 0 ekt
⟹ 0.9985 N 0=N0 ek∗1
⟹ 0.9985=ek
Now taking natural log both sides, we have
⟹ ln 0.9985=ln ek
⟹ ln 0.9985=k∗ln e
⟹ ln 0.9985=k ∴ ln e=1
k =−0.0015
Now conditions at half-life period (t1/2)
at t1
2
N = N 0
2
Therefore,
N=N 0 ekt becomes
⟹ N0
2 =N 0 e
k t 1
2
⟹ 1
2 =ek t 1
2
Taking natural log both sides, we have
⟹ ln 0.5=ln ekt 1
2
⟹ ln 0.5=k t1
2
∗ln e ∴ ln e=1
Then,

⟹−0.69314=−0.0015 t1
2
⟹ t1
2
=462.098 years
6. The population of a small country increases according to the
function B ( t )=1900000e0.04 t where t is measured in years. How many
people will the country have after 8 years?
Solution: The population of small country increases according to the function equation:
B ( t )=1900000e0.04 t ∴ where t is∈ years
After 8 years, t=8
B ( 8 )=1900000 e0.04∗8
B ( 8 )=1900000 ×1.377
B ( 8 )=2616300
Population after 8 years will be 2616300.
7. Find the value of the expression.
ln ( e−2 )
Solution: Let y=ln ( e−2 )
y=−2∗lne
y=−2∴ ln e=1
8. Express as a single logarithm and, if possible, simplify
1
2 loga x+ 4 loga y−3 loga x
Solution:

We see that base of the logarithm is same i.e “a”
¿ 1
2 loga x+ 4 loga y−3 loga x
¿ log a x
1
2 + loga y4−loga x3
¿ log a ( x
1
2 × y4 ) −loga x3
¿ loga ( x
1
2 × y4
x3 )
¿ loga ( x
1
2 × y4
x3 )
¿ log a ( x ( 1
2−3 ) × y4 )
¿ loga ( x ( −5
2 ) × y4 )
¿ loga
( y 4
x
5
2 )
Solve the equation. Give your answer as a decimal rounded to the nearest
thousandth.
9. 2x=36
Solution: 2x=36
Taking natural log both sides, we have
ln 2x=ln 36

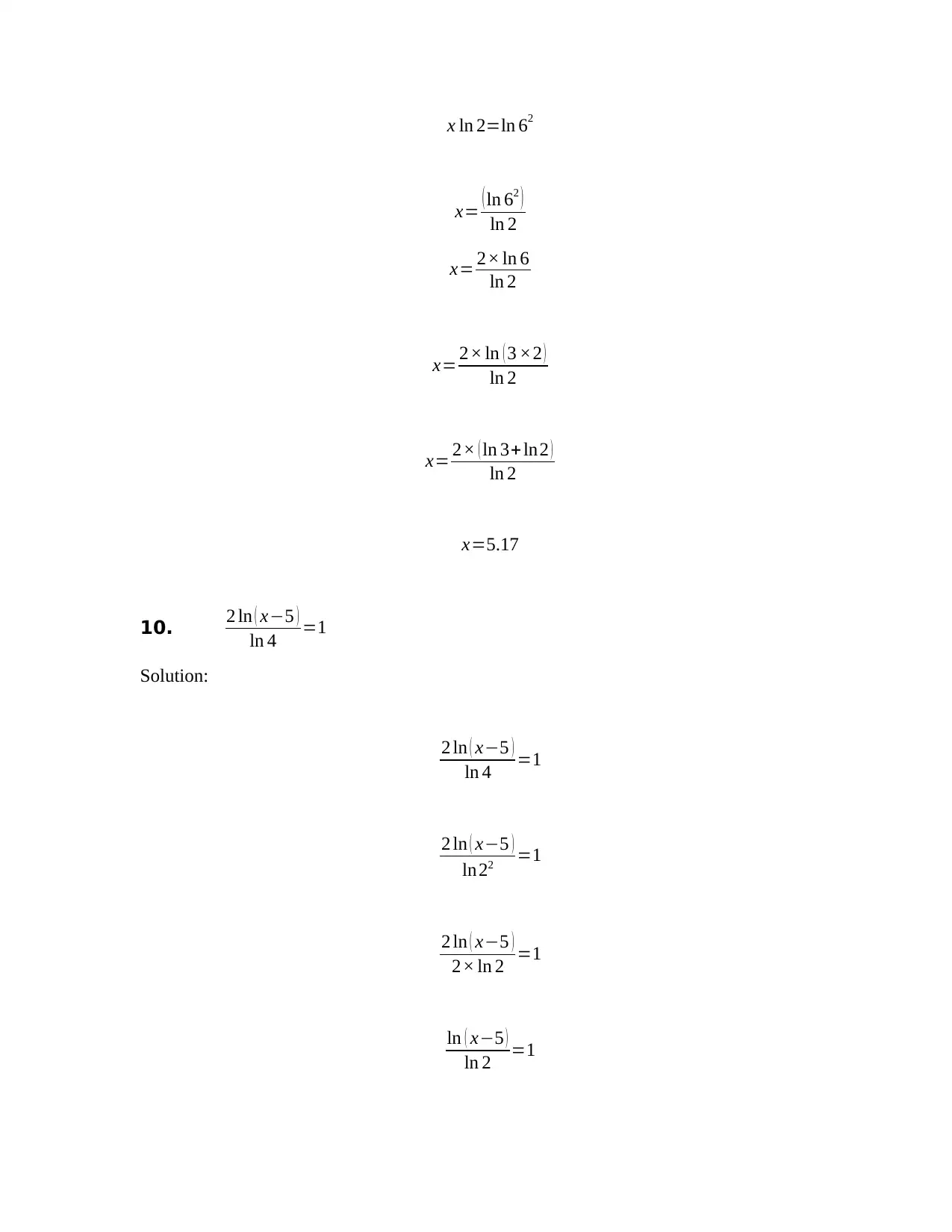
x ln 2=ln 62
x= ( ln 62 )
ln 2
x= 2× ln 6
ln 2
x= 2× ln ( 3 ×2 )
ln 2
x= 2× ( ln 3+ ln2 )
ln 2
x=5.17
10. 2 ln ( x−5 )
ln 4 =1
Solution:
2 ln ( x−5 )
ln 4 =1
2 ln ( x−5 )
ln22 =1
2 ln ( x−5 )
2× ln 2 =1
ln ( x−5 )
ln 2 =1

ln ( x−5 )=ln 2
(x−5)=2
x=7