Math 2100 Winter 2020: Area, Volume, and Curve Integration

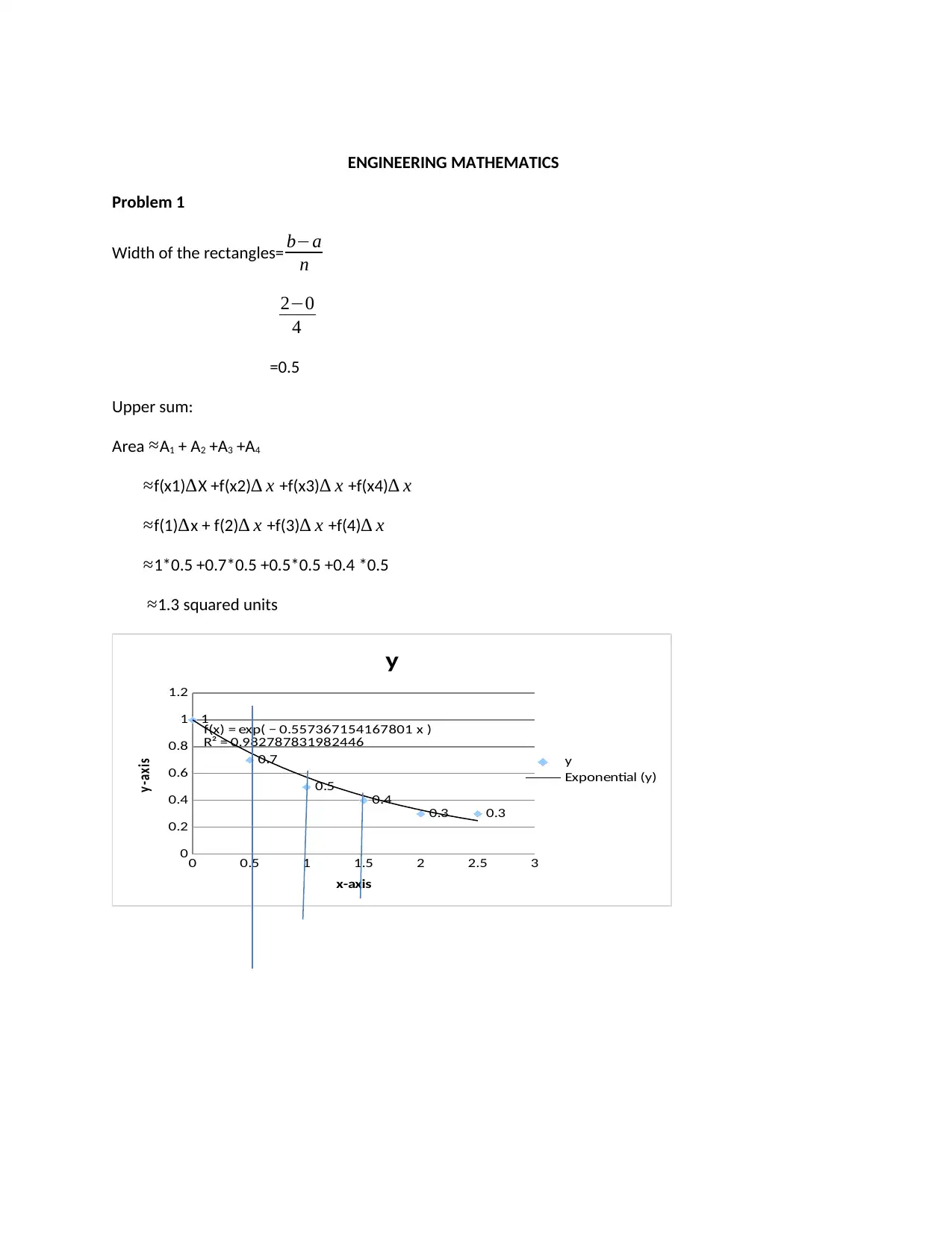
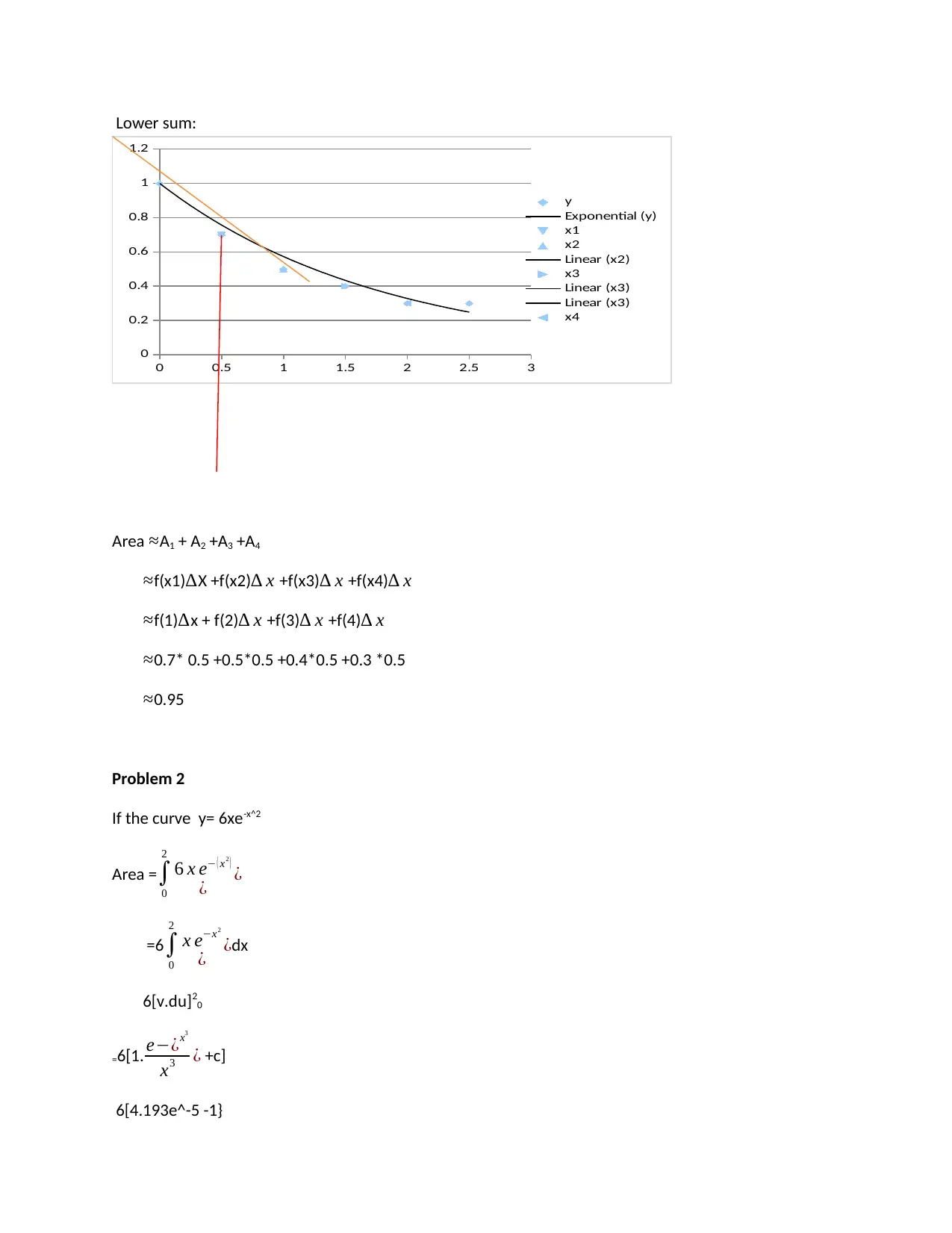
This assignment provides solutions to a Math 2100 test, focusing on calculus concepts such as area approximation using the rectangular method, definite integrals, and volume calculations. The solutions cover finding the area under a curve, the area bounded by two curves, and the volume of solids of revolution generated by rotating curves around the x-axis and y-axis. Detailed step-by-step calculations are presented for each problem, including the use of definite integrals and the application of formulas for volumes of revolution. The solutions also include the final answers with the correct units, which are square units for area and cubic units for volume. The assignment is designed to help students understand and apply fundamental calculus principles in solving geometric problems.

ENGINEERING MATHEMATICS
Problem 1
Width of the rectangles= b−a
n
2−0
4
=0.5
Upper sum:
Area ≈A1 + A2 +A3 +A4
≈f(x1)∆X +f(x2)∆ x +f(x3)∆ x +f(x4)∆ x
≈f(1)∆x + f(2)∆ x +f(3) ∆ x +f(4)∆ x
≈1*0.5 +0.7*0.5 +0.5*0.5 +0.4 *0.5
≈1.3 squared units
0 0.5 1 1.5 2 2.5 3
0
0.2
0.4
0.6
0.8
1
1.2
1
0.7
0.5
0.4
0.3 0.3
f(x) = exp( − 0.557367154167801 x )
R² = 0.982787831982446
y
y
Exponential (y)
x-axis
y-axis

Lower sum:
0 0.5 1 1.5 2 2.5 3
0
0.2
0.4
0.6
0.8
1
1.2
y
Exponential (y)
x1
x2
Linear (x2)
x3
Linear (x3)
Linear (x3)
x4
Area ≈A1 + A2 +A3 +A4
≈f(x1) ∆X +f(x2)∆ x +f(x3) ∆ x +f(x4)∆ x
≈f(1)∆x + f(2)∆ x +f(3)∆ x +f(4)∆ x
≈0.7* 0.5 +0.5*0.5 +0.4*0.5 +0.3 *0.5
≈0.95
Problem 2
If the curve y= 6xe-x^2
Area =∫
0
2
6 x e− ( x2 )
¿ ¿
=6 ∫
0
2
x e−x2
¿ ¿dx
6[v.du]20
=6[1. e−¿x3
x3 ¿ +c]
6[4.193e^-5 -1}

=5.999 squared units
Problem 3
Area =∫
0
4
(5 x−x2) dx -∫
0
4
x dx
= [ 5 x2
2 − x3
3 +c ]40 - ( x2
2 +c)40
={( 5∗16
2 - 64
3 ) –(0) } –{( 16
2 )–(0)}
=¿ - 64
3 ¿ - 16
2
= 112
6 - 16
2
= 112−48
6
= 64
6
=10 2
3 squared units.
Problem 4
Rotating the curve about the y-axis, you will construct something that looks like cone i.e a hollow cone
with a curve inside.
The cross-section of the cone is circular in nature with x= 1
2 y2+ 8as the radius

Hence ,the cross-sectional area is equal to :
=⫪(r)2
Volume =∫
a
b
⫪ ¿ ¿
Volume = ∫
−4
4
⫪ ( 1
2y2 +8) dy
=⫪ [ y3
6 +8 y +c ]4-4
= ⫪ {
[ 64
6 +32 ]-[ −64
6 −32 ]}
=⫪{42 2
3 --42 2
3}
=85 1
3 ⫪cubic units.
Problem 5
Rotating the two curves about the x-axis, you will construct something that looks like cone i.e a hollow
cone with a curve inside.
The cross-section of the cone is circular in nature with y= √cosx+1 as the outer radius and y = 2
⫪ as
the inner radius.
Hence ,the area of the inner cross-section is equal to :
=⫪(router)2 -⫪(rinner)2
Volume =∫
a
b
⫪ ¿ ¿ -∫
a
b
⫪ ¿ ¿ dx
=∫
0
⫪
2
⫪ ¿ ¿)2 dx -∫
0
⫪
2
⫪ ¿ ¿) dx

= ∫
0
⫪
2
⫪ ( cosx +1 ) dx−∫
0
⫪
2
4
⫪
x2
=⫪(sin(x) +x)⫪/20 -{ 4
⫪ ( ( ⫪
2 )3
3
-0}
=⫪(sin( ⫪
2 ) + 4
⫪( ⫪3
24 -0)
=⫪(1) + ⫪
2 + 4 ⫪2
24
=⫪ + ⫪
2 + ⫪2
6
=⫪ + 3⫪2−⫪2
6
=⫪+ 2⫪2
3 cubic units.