Math Assessment 1: Trigonometry, Calculus, Algebra and Integration
VerifiedAdded on 2023/01/03
|27
|3448
|34
Homework Assignment
AI Summary
This document provides a complete solution set for Math Assessment 1. The assessment covers a wide range of mathematical concepts including arithmetic and geometric progressions, infinite series, binomial expansions, and sketching trigonometric graphs. It explores trigonometric identities, equations, and applications within right-angled triangles. Additionally, the solutions delve into calculus, addressing differentiation, integration, and the application of substitution methods. Further, the document includes solutions to differential equations, partial fraction decomposition, and parametric equations. The assignment also assesses understanding of limits, series convergence, and basic algebraic manipulations. The solutions offer detailed step-by-step explanations to ensure a comprehensive understanding of each problem.
1 out of 27




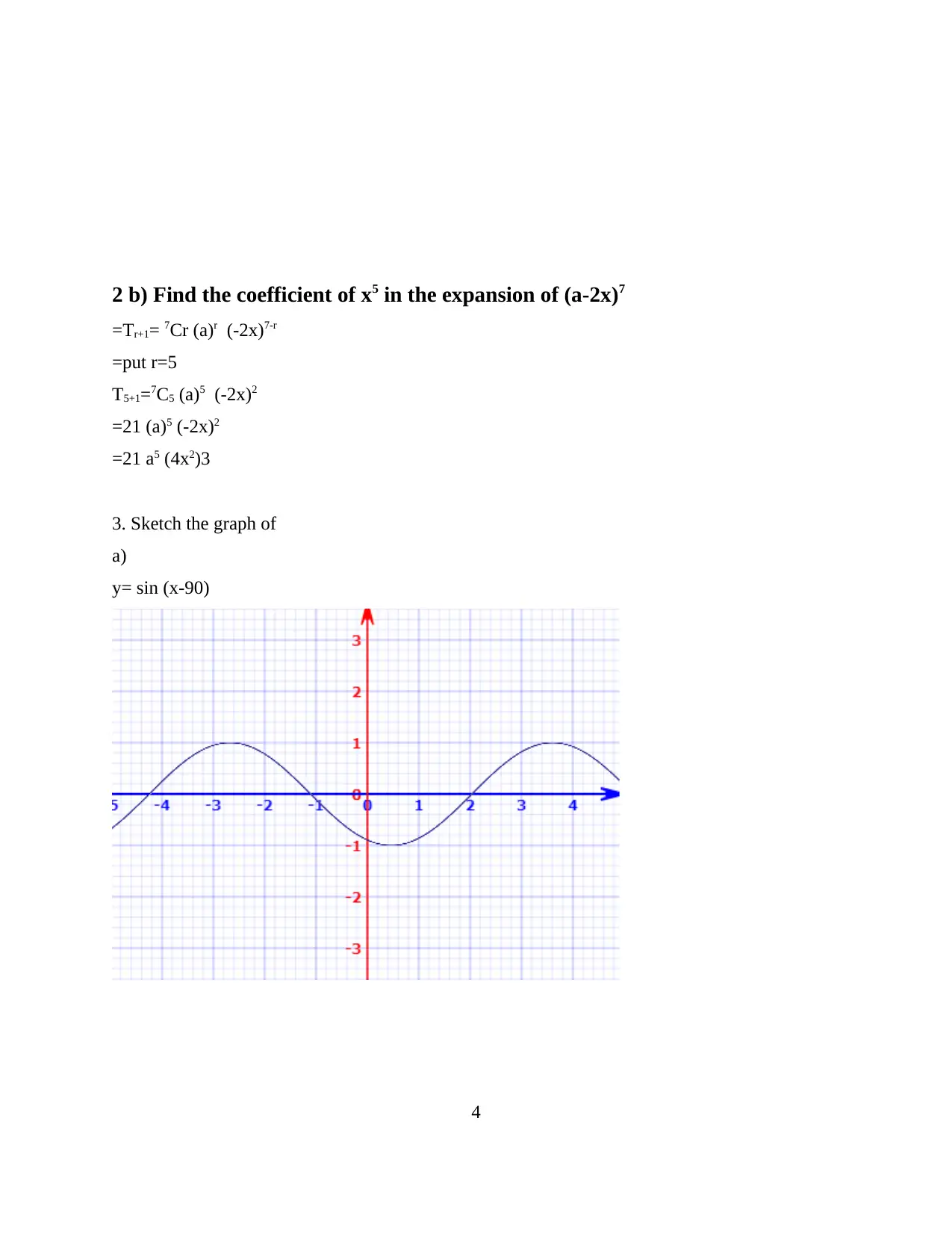
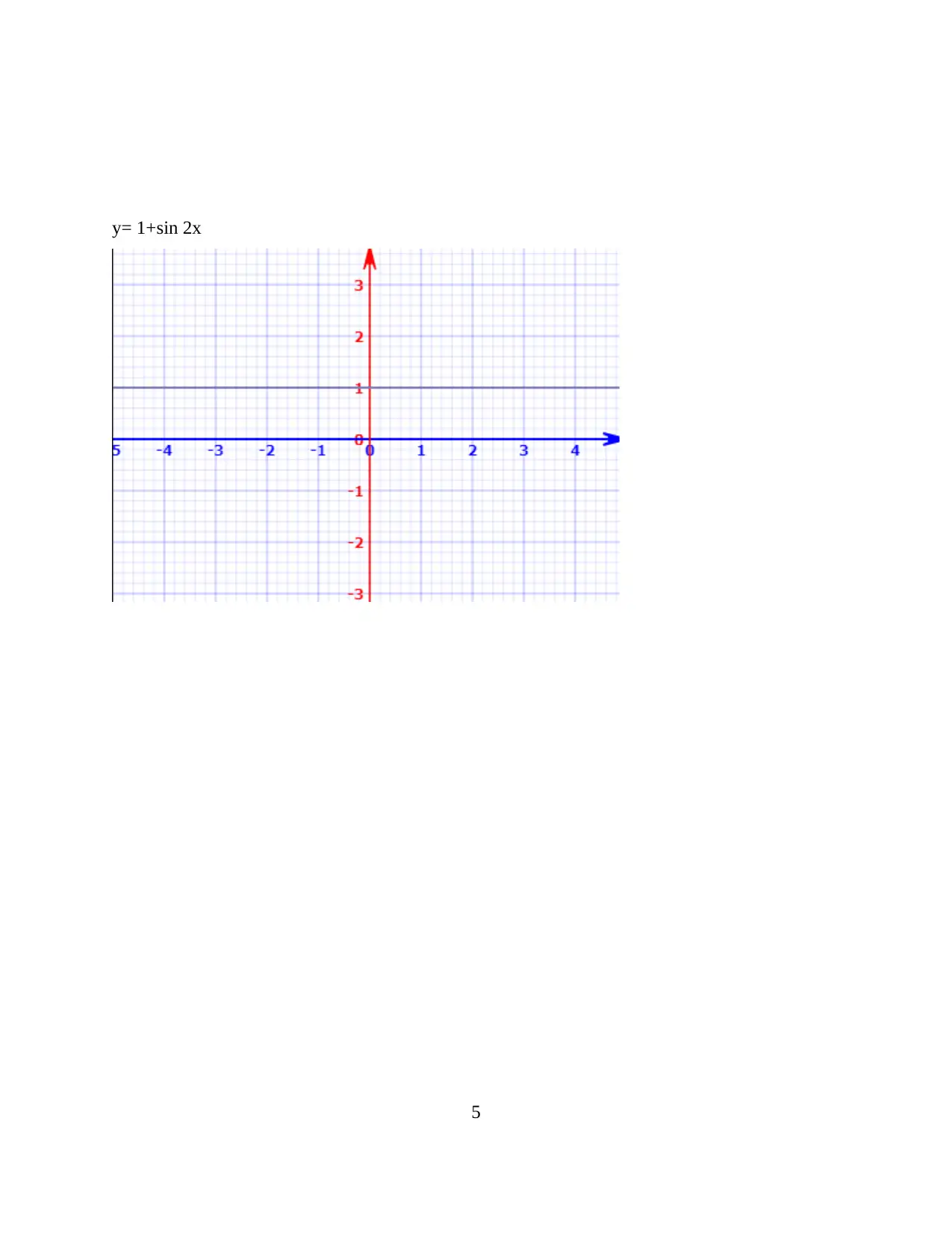
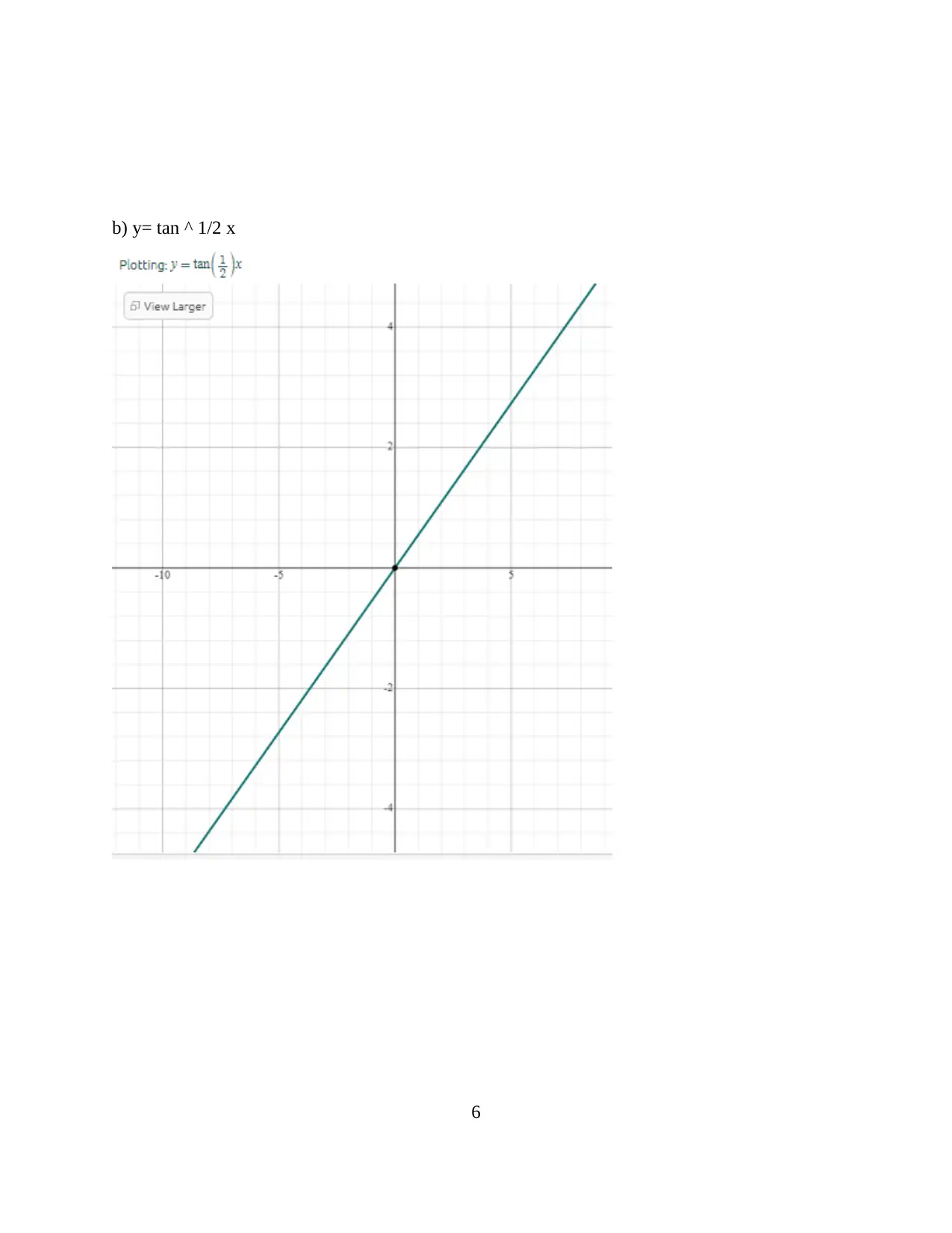
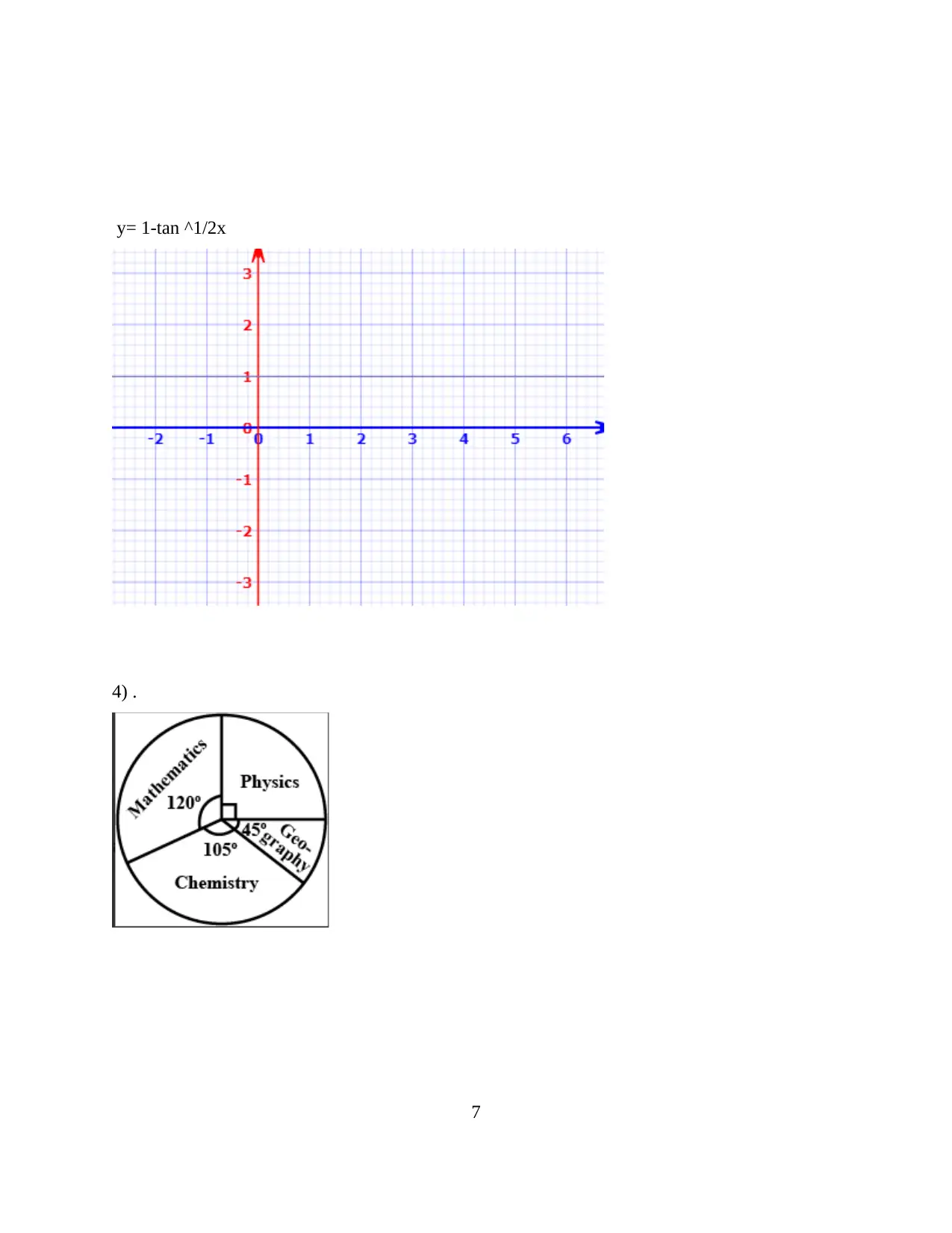


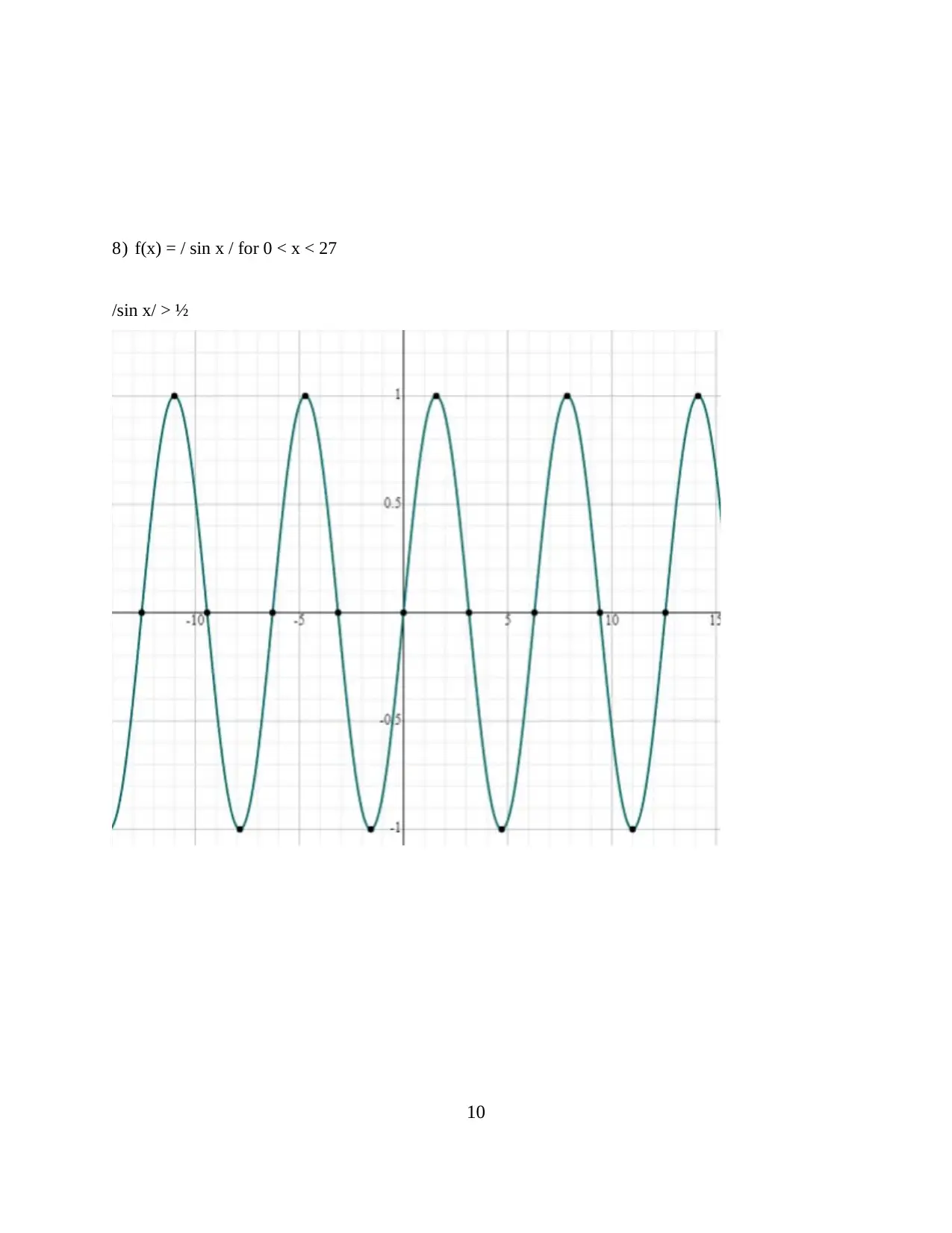
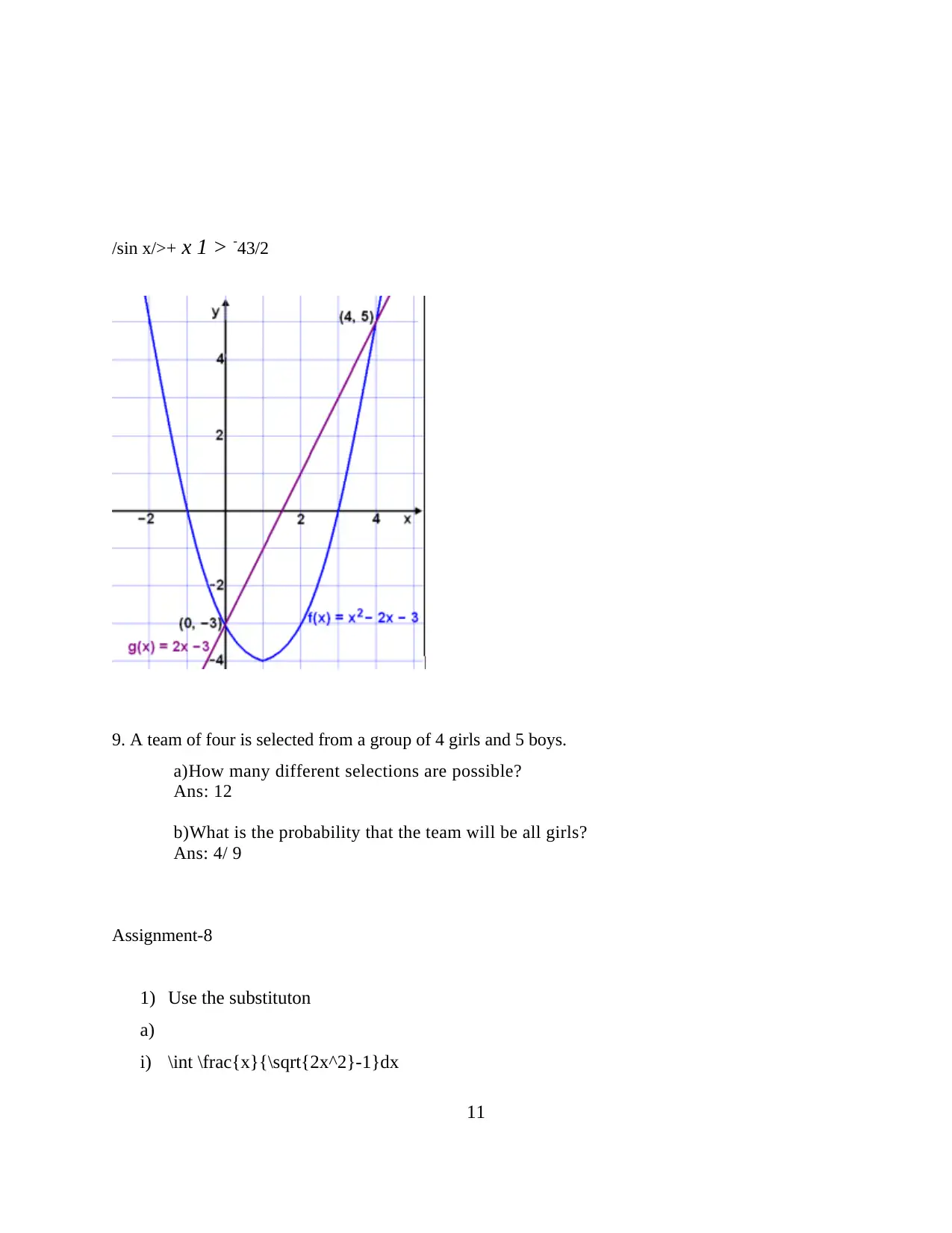





![[object Object]](/_next/static/media/star-bottom.7253800d.svg)