MATH130 Assignment 2: Detailed Algebra Problem Solutions
VerifiedAdded on 2022/11/14
|8
|1034
|462
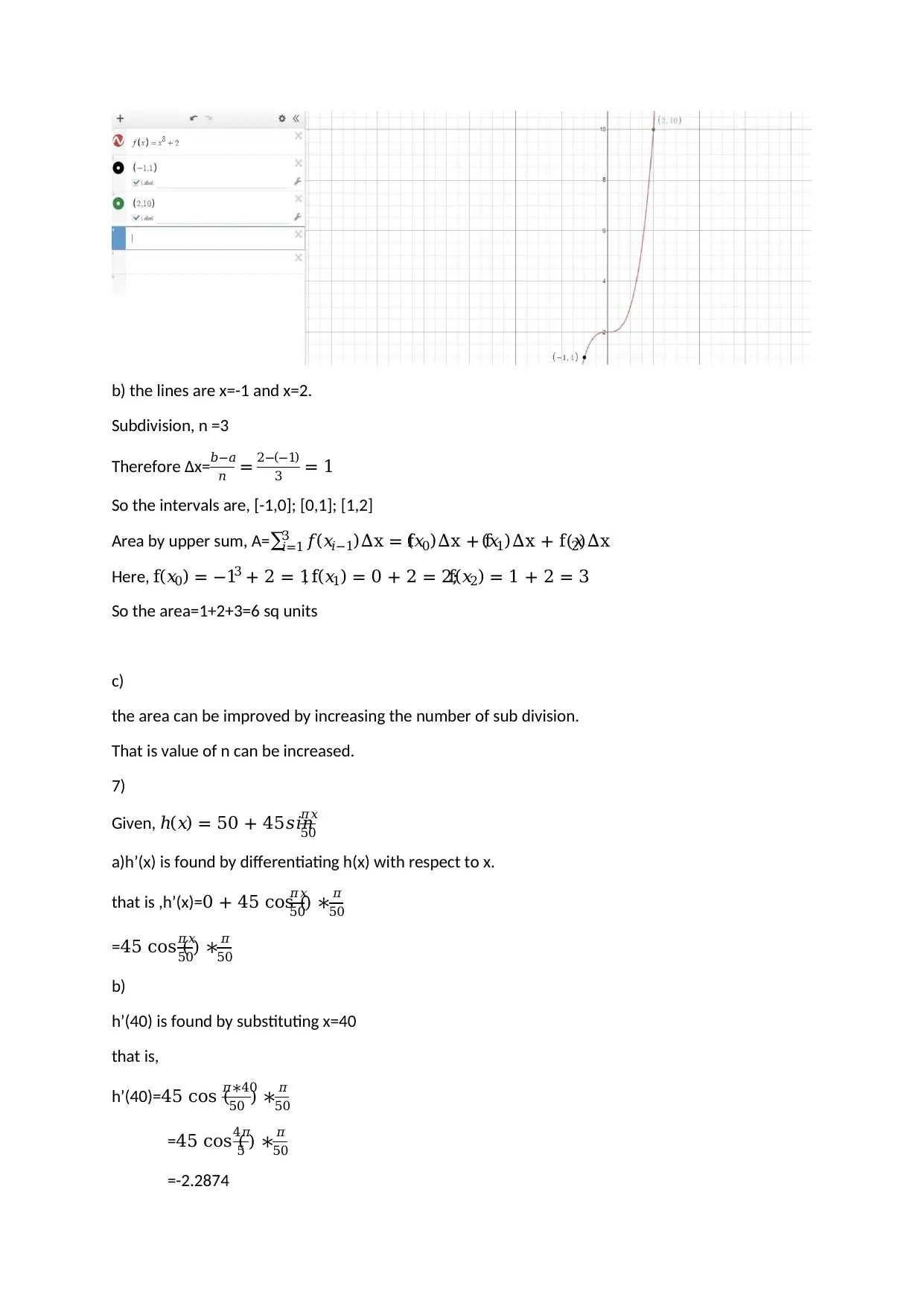
Homework Assignment
AI Summary
This document contains the complete solutions for MATH130 Assignment 2, focusing on algebra concepts. The assignment includes problems related to exponential decay, where the quantity of medicine in a patient's bloodstream decreases over time, requiring the formulation of equations and determination of the halving time. Trigonometry problems involve the unit circle and trigonometric identities, specifically dealing with cosine and sine functions. Calculus problems involve finding marginal revenue, area calculations using upper sums, and derivative applications to determine the rate of change and maximum/minimum values of a function. The solutions include step-by-step explanations, graphical representations, and detailed calculations to demonstrate the problem-solving process.
1 out of 8





![[object Object]](/_next/static/media/star-bottom.7253800d.svg)