MATH1040/MATH7040 Assignment 2: Linear Equations, Functions Analysis

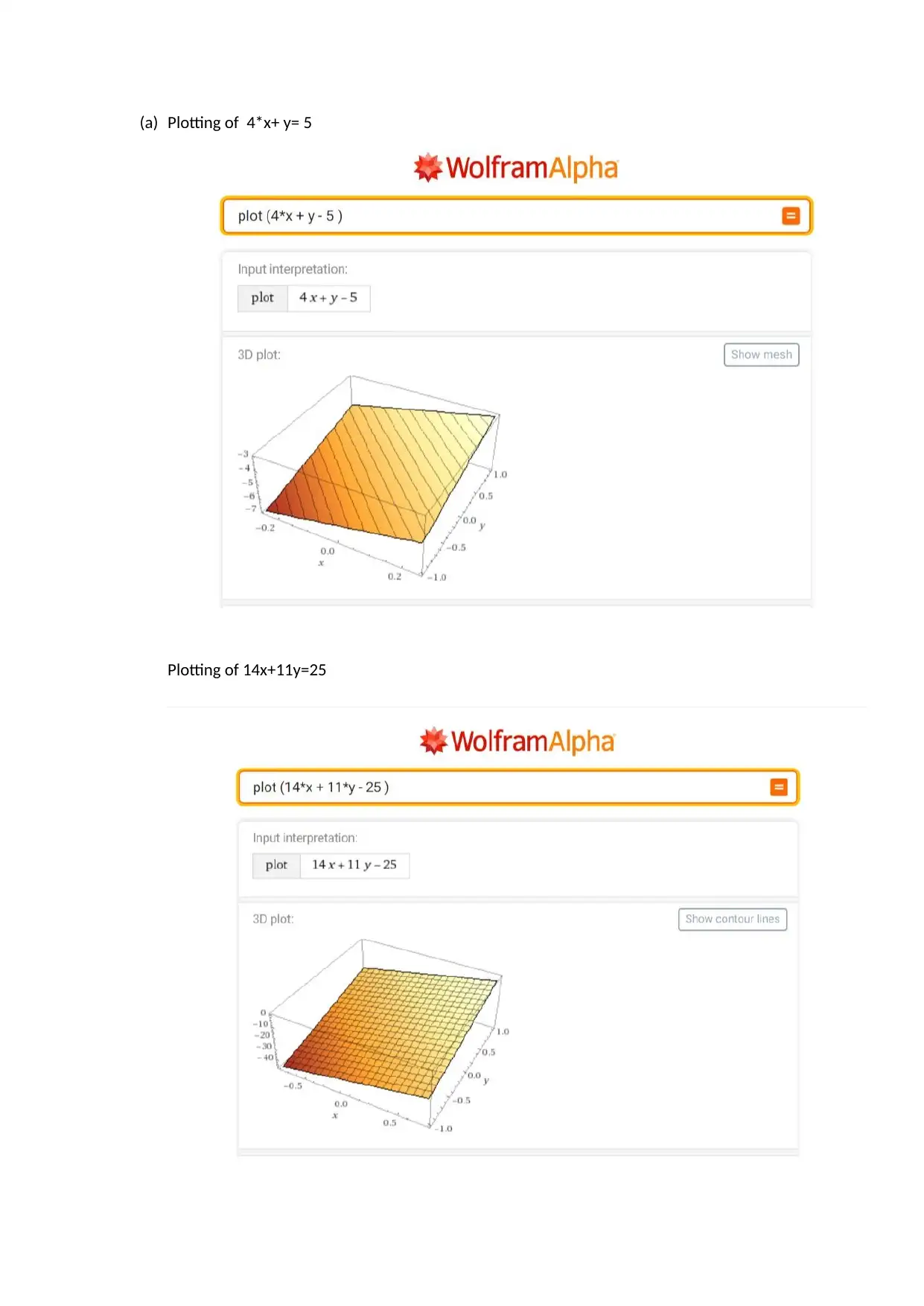
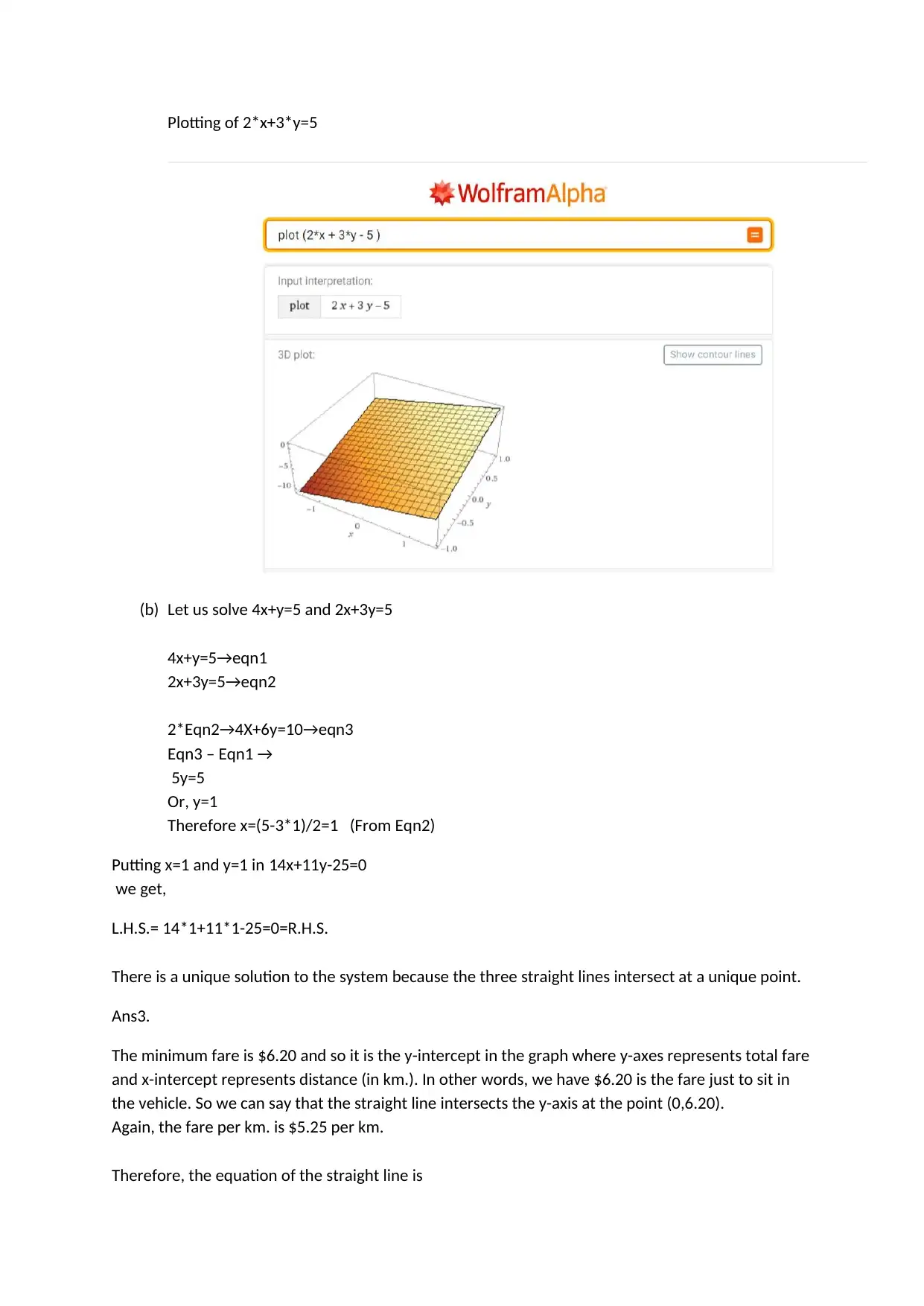
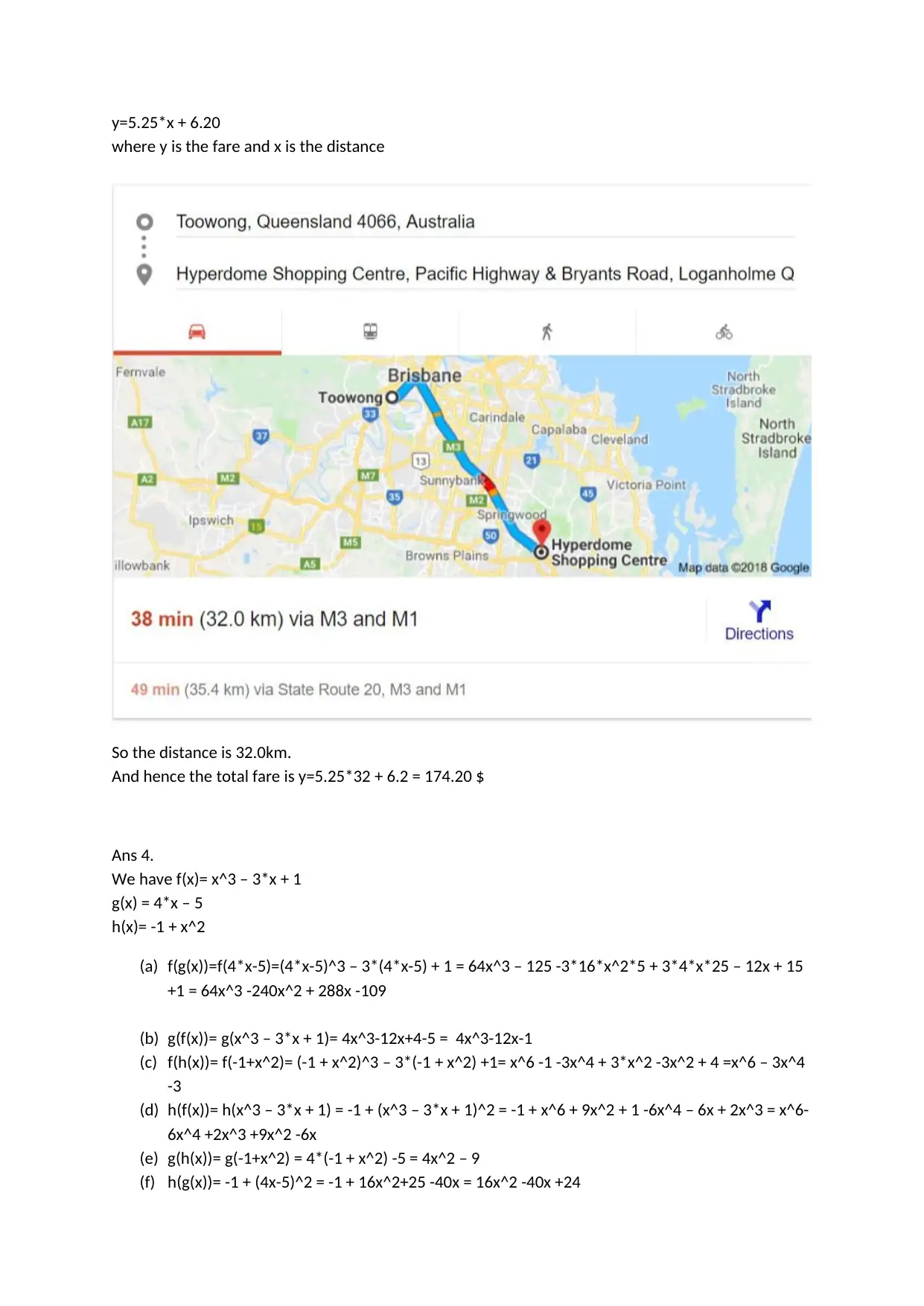
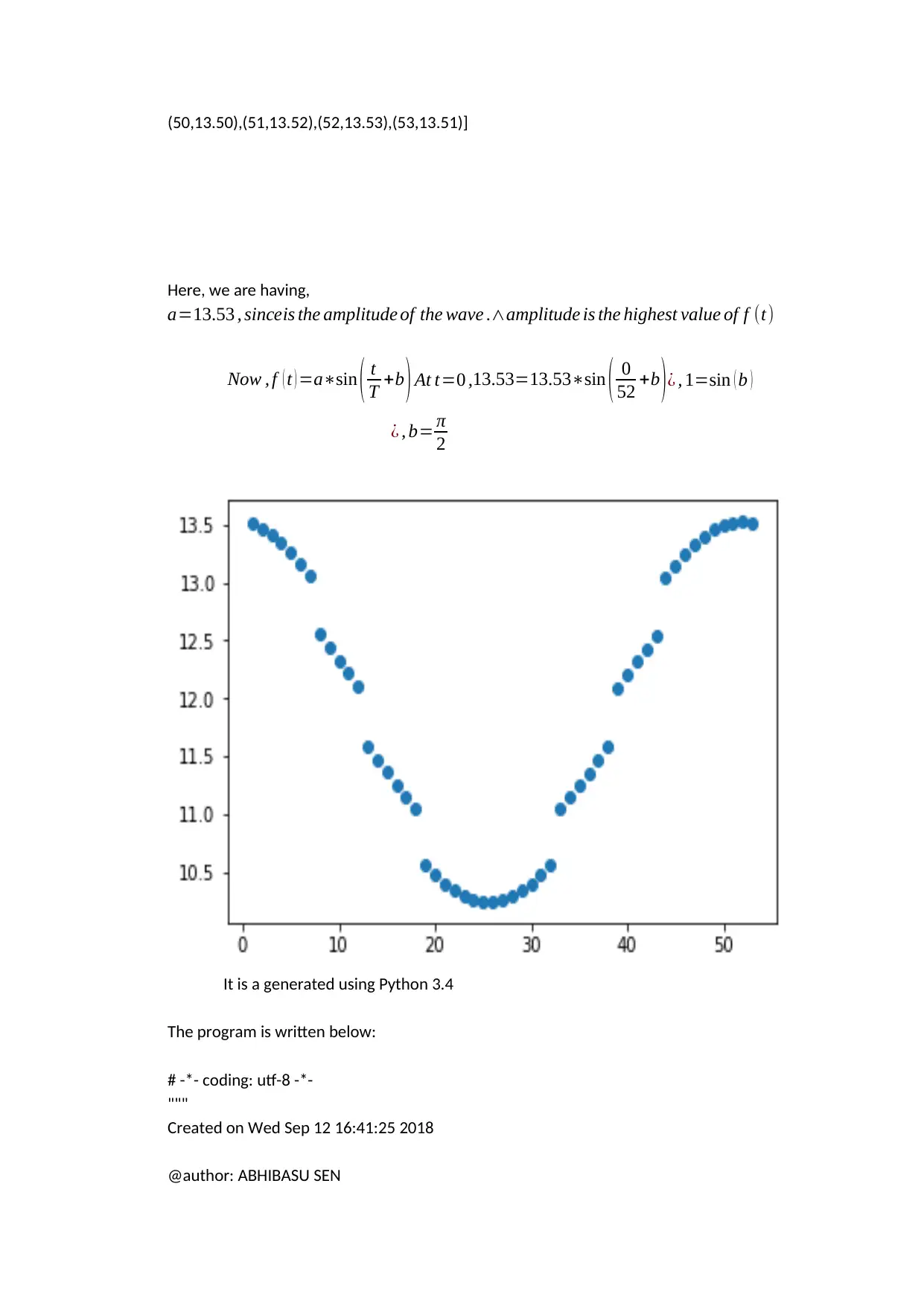
This assignment solution covers several mathematical concepts, including collinearity of points, solving systems of linear equations, and function analysis. The first question demonstrates that a given set of points are collinear by finding the equation of the straight line passing through them and verifying that the other points satisfy the equation. The second question involves finding the point of intersection of two lines. The third question determines the equation of a line based on a minimum fare and per-kilometer charge. The fourth question focuses on function composition, evaluating f(g(x)), g(f(x)), f(h(x)), h(f(x)), g(h(x)), and h(g(x)) for given functions f(x), g(x), and h(x). The fifth question determines the quadratic function representing the price per kilo of bananas and calculates the price for a specific value. Lastly, the sixth question involves analyzing a given dataset to determine the amplitude and phase shift of a sine wave and includes a Python program used to generate the data and a corresponding plot.

Ans1. (a)
The equation of the straight line passing through (x1,y1) and (x2,y2) is
y-y1=((y2-y1)/(x2-x1))(x-x1)
Now the equation of the straight line passing through (-4, 20) and ( -2.5 , 15.5 ) is:
y-20=((15.5-20)/(-2.5-(-4)))(x-(-4))
Or, y-20= ((-4.5)/(1.5))(x+4)
Or, y-20=-3x-12
Or, 3x+y-8=0
Now taking the first point i.e. x=-2 and y=14, we get,
L.H.S.= 3*(-2)+14-8=0=R.H.S.
Taking x=-1.5 and y=12.5, we get,
L.H.S.= 3*(-1.5)+12.5-8=0=R.H.S.
Taking x=-1 and y=11, we get,
L.H.S.=3*(-1)+11-8=0=R.H.S.
Hence we can see that the points, (-2,14), (-1.5,12.5) and (-1,11) are collinear.
(b)
Here, L=2x-5y-9=0 -> eqn.1
And L’ = 3x+y-8=0 -> eqn.2
To find the intersection,
3*eqn.1→6x-15y-27=0→eqn.3
2*eqn.2→6x+2y-16=0→eqn.4
Now, eqn4-eqn.3→17y-11=0
or, y=11/17
Therefore, x= (9+5y)/2=104/17
So, they intersect at (104/17, 11/17)
Ans2.

(a) Plotting of 4*x+ y= 5
Plotting of 14x+11y=25

Plotting of 2*x+3*y=5
(b) Let us solve 4x+y=5 and 2x+3y=5
4x+y=5→eqn1
2x+3y=5→eqn2
2*Eqn2→4X+6y=10→eqn3
Eqn3 – Eqn1 →
5y=5
Or, y=1
Therefore x=(5-3*1)/2=1 (From Eqn2)
Putting x=1 and y=1 in 14x+11y-25=0
we get,
L.H.S.= 14*1+11*1-25=0=R.H.S.
There is a unique solution to the system because the three straight lines intersect at a unique point.
Ans3.
The minimum fare is $6.20 and so it is the y-intercept in the graph where y-axes represents total fare
and x-intercept represents distance (in km.). In other words, we have $6.20 is the fare just to sit in
the vehicle. So we can say that the straight line intersects the y-axis at the point (0,6.20).
Again, the fare per km. is $5.25 per km.
Therefore, the equation of the straight line is

y=5.25*x + 6.20
where y is the fare and x is the distance
So the distance is 32.0km.
And hence the total fare is y=5.25*32 + 6.2 = 174.20 $
Ans 4.
We have f(x)= x^3 – 3*x + 1
g(x) = 4*x – 5
h(x)= -1 + x^2
(a) f(g(x))=f(4*x-5)=(4*x-5)^3 – 3*(4*x-5) + 1 = 64x^3 – 125 -3*16*x^2*5 + 3*4*x*25 – 12x + 15
+1 = 64x^3 -240x^2 + 288x -109
(b) g(f(x))= g(x^3 – 3*x + 1)= 4x^3-12x+4-5 = 4x^3-12x-1
(c) f(h(x))= f(-1+x^2)= (-1 + x^2)^3 – 3*(-1 + x^2) +1= x^6 -1 -3x^4 + 3*x^2 -3x^2 + 4 =x^6 – 3x^4
-3
(d) h(f(x))= h(x^3 – 3*x + 1) = -1 + (x^3 – 3*x + 1)^2 = -1 + x^6 + 9x^2 + 1 -6x^4 – 6x + 2x^3 = x^6-
6x^4 +2x^3 +9x^2 -6x
(e) g(h(x))= g(-1+x^2) = 4*(-1 + x^2) -5 = 4x^2 – 9
(f) h(g(x))= -1 + (4x-5)^2 = -1 + 16x^2+25 -40x = 16x^2 -40x +24

Ans5.
Since the price per kilo of banana is quadratic, so we are having a function like this:
f ( t ) =a∗t2 +b∗t+ 2Now, we are having, 6.25=a∗52+ b∗5+2→eqn1
& 56=a∗302 +b∗30+2→eqn2
Now, 6.25=25∗a+5∗b+256=900∗a+30∗b+2
6.25∗6=150 a+30 b+1 2 ( Multiplying eqn 1by 6 ) 37.5=150∗a+30∗b+12→eqn3
eqn 2−eqn 3 gives ,56−37.5=750∗a−1 0a=0.0 38
Therefore , ¿ eqn 3 we get37.5=150∗0.038+30∗b+ 12b=0. 66
So, the equation becomes,
f ( t )=0.038∗t 2+ 0.66∗t+2
Now putting t=12 , the price of 1 kilo of banana becomes ,f ( t )=0.038∗122 +0.66∗12+2
f ( t )=5.472+7.92+2f ( t )=1 5.392So ,the number of kilos of bananas that can be bought
¿ 200
15.392=13
Ans6.
The list is given below:
[(1,13.51),(2,13.47),(3,13.41),(4,13.34),(5,13.26),(6,13.16),(7,13.06),(8,12.56),(9,12.44),
(10,12.33),(11,12.22),(12,12.10),(13,11.58),(14,11.47),(15,11.36),(16,11.25),(17,11.15),
(18,11.05),(19,10.56),(20,10.47),(21,10.40),(22,10.34),(23,10.29),(24,10.26), (25,10.24),
(26,10.24),(27,10.26), (28,10.29),(29,10.34),(30,10.40),(31,10.48),(32,10.56),(33,11.05),
(34,11.15),(35,11.25),(36,11.35),(37,11.46),(38,11.58),(39,12.09),(40,12.20),(41,12.32),
(42,12.43),(43,12.54),(44,13.05),(45,13.15),(46,13.24),(47,13.33),(48,13.40),(49,13.46),

(50,13.50),(51,13.52),(52,13.53),(53,13.51)]
Here, we are having,
a=13.53 , sinceis the amplitude of the wave .∧amplitude is the highest value of f (t)
Now , f ( t ) =a∗sin ( t
T +b ) At t=0 ,13.53=13.53∗sin ( 0
52 +b )¿ , 1=sin ( b )
¿ , b= π
2
It is a generated using Python 3.4
The program is written below:
# -*- coding: utf-8 -*-
"""
Created on Wed Sep 12 16:41:25 2018
@author: ABHIBASU SEN

"""
importnumpy as np
frommatplotlib import pyplot as plt
data = np.array([[1,13.51],[2,13.47],[3,13.41],[4,13.34], [5,13.26] , [6,13.16] , [7,13.06] ,
[8,12.56] , [9,12.44] , [10,12.33] ,[11,12.22],[12,12.10],[13,11.58],[14,11.47],[15,11.36],
[16,11.25],[17,11.15],[18,11.05],[19,10.56],[20,10.47],[21,10.40],[22,10.34],[23,10.29],
[24,10.26], [25, 10.24], [26,10.24],[27,10.26], [28,10.29],[29,10.34],[30,10.40],[31,10.48],
[32,10.56],[33,11.05],[34,11.15],[35,11.25],[36,11.35],[37,11.46],[38,11.58],[39,12.09],
[40,12.20],[41,12.32],[42,12.43],[43,12.54],[44,13.05],[45,13.15],[46,13.24],[47,13.33],
[48,13.40],[49,13.46],[50,13.50],[51,13.52],[52,13.53],[53,13.51]])
x, y = data.T
plt.scatter(x,y)