MTH211 Fundamentals of Mathematical Methods TMA Solution 2020

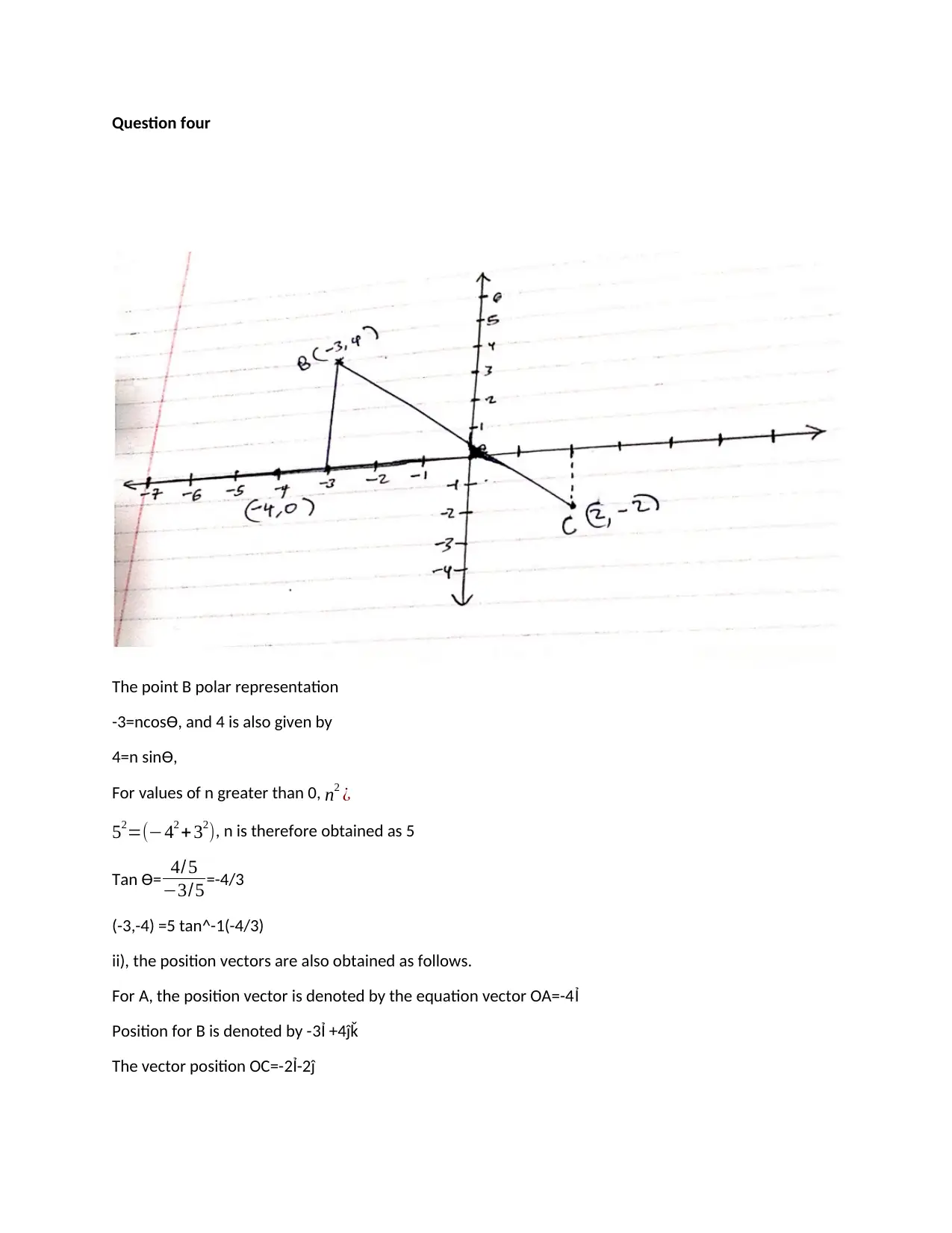
This document presents a comprehensive solution to the MTH211 Fundamentals of Mathematical Methods and Mechanics Tutor-Marked Assignment (TMA) from January 2020. The solution addresses several key mathematical concepts, including implicit differentiation, where the derivative of a curve is found, and the equation of the tangent is presented. It also covers the evaluation of integrals using differentiation and integration methods. Furthermore, the solution includes an application of Euler's approximation method to find approximate values for a function, along with the calculation of global error. It also deals with polar representation and vector positions, offering solutions for points and vectors in polar coordinates. Finally, the document addresses a physics-related problem, involving the calculation of force components acting on a block, providing a complete solution to the assignment questions.

Mathematical solution
Name
Institution

Question one
a) (i) range on the left side (x>0)
(y>-3)
Ii
ln ( y ) −ln ( y+ 3 ) +ln 4=2 ln (x)
Adding ln(y+3) on both sides
lny+ ln 4=2 ln ( x ) + ln ( y +3)
From log rule, we obtain
ln ( y .4 ) =2lnx+ ln( y +3)
ln ( y .4 ) =ln ( x2 ) +ln( y +3)
ln ( y .4 ) =ln ( x2 )( y +3)
y .4= ( x2 ) ( y +3)
Making y the subject of the formula,
y= 3 x2
4−x2
b)
dy
dx of x3−2 xy+ y2
x3−2 xy+ y2=1
Both sides of the equation is differentiated with respect to x,
dy
dx ( x¿¿ 3−2 xy + y2)= dy
dx 1 ¿
dy
dx ( x¿¿ 3−2 xy + y2)=3 x2−2 ¿ ¿+2y d
dx y
d
dx ( 1 )=0
3 x2−2 ¿+2y d
dx y=0

The equation is rewritten as
3 x2−2 ¿+2yy’=0
Isolating y’=1
y ’=−3 x2−2 y
2(−x+ y )
y ’=−3 x2−2 y
2(−x+ y )
d
dx ( y ) −3 x2−2 y
2(−x + y )
By substituting values of x and y, 1 and 2
d
dx ( y ) −3 x 12 −2 x 2
2 (−1+2)
=-0.5
-0.5= y−2
x−1
y-2=-1/2x+0.5
y=0.5x-1.5
C (i)
∫
0
1
v3
v 4 +5 dv
1
4 (Ln6-Ln5) which is equals top 0.04558

Substituting u for the term denoted by v4 +5, ∫
5
6
1
4 u dv, Results from taking the constant out
∫
a
b
f ( x ) dx=a . f ( x ) dx
= 1
4 . (∫
5
6
1
u du)
Applying the use of Domain integral,
∫
a
b
1
u du=LnIuI
= 1
4 . LnIuI ¿the range of 5 ¿ 6
By performing boundary computation, Ln (6)-ln (5)
This therefore results, ¼(Ln (6)-ln (5))
(ii)
∫
2
5
t
t−1 dt
∫
2
5
t
√t−1 dt=20 /3
Ensuring the substitution for the term √t−1 , by a single term u,
∫
1
2
2 ( u2 +1 ) du
=2. ∫
1
2
( u2 ) +∫
1
2
( 1 ) duEnsuring the application of the sum rule.
∫
1
2
( f + g ) dx∫
1
2
( fdx ) +∫
1
2
( gdx ) dx

The manipulation tehrfore becomes
∫
1
2
( u2 ) du= 7/3
∫
1
2
( 1 ) du=1
2(7/3 +1)
Simplifying we obtain,
2(7/3 +1)
=20/3
Question two

dy
dx = x2 +3
y f (x , y)=1= f 0 ,=¿ 1, x0 ,=¿0 ,¿¿
Part 1 of the Euler’s approximation method.
Y( xn+1 = y n+1 = yn +h∗f ( xn , yn )
Where xn+1 = xn +h , his∈step wiseconnotation .
The first integration,

n=0
(x1 =x0 + h=0+ 0.1
Y (x1 = y0.1 = y1= y0 + 0.1∗x0
2 +3
y0
=1+ 0.1∗00
2 +3
10
=¿1.3
Y (0.1) =1.3
The second iteration
n=1
( x2 =x1 + h=0.1+0.1=0.2
Y (x2 = y0.1 = y2 = y01 + 0.1∗x 12+3
y1
=1.3+ 0.1∗0.12 +3
1.3 =¿1.5315
Y (0.2) =1.531538
The third iteration
n=2
( x3 =x2+ h=0.2+ 0.1=0.3
Y (x3= y0.3 = y3= y2 +0.1∗x 22 +3
y2
=1.531538+ 0.1∗0.12+3
1.3 =¿1.730031
Y (0.2) =1.730031
This value provides the approbation for the value of y (0.3)
Numerical approximation for global error at x is achieved through the following definition.
En=¿ yxn− yn ¿
The exact approximation values for xn are therefore denoted by the values of yxn∧ y n
The global error for the above problem is thud denoted by the equation
En +1=the magnitue of yxn +1− yn+ 1
The solution for the above equation for the value of x =2 is obtained as
yx2=2 ¿)
Substituting for the values of y (0), x=0.3
Y (0.3) is therefore obtained as 1.678689

E3 =themagnitue of yx3− y3
En +1=the magnitue of yx3 − y3
1.676886-1.730031=0.051542, the obtained value is the global required error.
Question three

Question four
The point B polar representation
-3=ncosƟ, and 4 is also given by
4=n sinƟ,
For values of n greater than 0, n2 ¿
52=(−42 + 32), n is therefore obtained as 5
Tan Ɵ= 4/ 5
−3/5 =-4/3
(-3,-4) =5 tan^-1(-4/3)
ii), the position vectors are also obtained as follows.
For A, the position vector is denoted by the equation vector OA=-4Ỉ
Position for B is denoted by -3Ỉ +4ĵǩ
The vector position OC=-2Ỉ-2ĵ