BTEC Engineering Maths Assignment: Mathematical Methods and Statistics

This document presents a comprehensive solution to an Engineering Maths assignment focusing on Mathematical Methods and Statistical Techniques. The assignment covers a range of problems, including dimensional analysis, series, circuit analysis, and statistical probability distributions. Part 1 of the assignment delves into problems involving dimensional analysis, arithmetic progressions, geometric progressions, and circuit analysis using resistors and capacitors. MATLAB simulation is used to analyze signals. Part 2 explores statistical techniques such as calculating mean and standard deviation, binomial probability, and Z-score analysis to determine percentages and probabilities. The document provides detailed solutions with equations, calculations, and explanations, along with references to relevant sources. The assignment is designed to enhance the understanding of real-world engineering and scientific problems, incorporating experiments and software analysis to provide a thorough understanding of the concepts.

Mathematical Methods and Statistical Techniques
M/615/1476
1/1/2020
[Type the company name]

Contents
Part 1:..........................................................................................................................................................3
Problem (a)..............................................................................................................................................3
Problem (b)..............................................................................................................................................4
Problem (c)..............................................................................................................................................5
Problem (d)..............................................................................................................................................6
Problem (e)..............................................................................................................................................7
Problem (f)...............................................................................................................................................8
Problem (g)............................................................................................................................................10
Problem (h)............................................................................................................................................11
Problem (i).............................................................................................................................................13
Part 2:........................................................................................................................................................15
Problem (a)............................................................................................................................................15
Problem (b)............................................................................................................................................16
Problem (c)............................................................................................................................................18
Problem (d)............................................................................................................................................20
Conclusion.................................................................................................................................................21
References.................................................................................................................................................22
2 | P a g e

Part 1:
Problem (a)
Solution:
The Dimensions of Power, P = ML^2T^-3
And the Dimension of Voltage, V = L^0.5 M^0.5 T^-1
3 | P a g e

Since the equation of power dissipation across the Resistor is given by
So, Resistance, R is given by
So, the Dimensions of R is
(L^0.5 M^0.5 T^-1)^2/ ML^2T^-3
= L^-1T^2
Problem (b)
Solution:
The LHS of the equation is time period of Vibration of string
t with Dimension [T]
the right hand side of the equation will have the dimension
2π = no dimension
m^3 = [M^3]
4 | P a g e

l= [L^1]
F = [MLT^−2]
So, as per equation RHS has dimensioned,
([M^3] [L^1]/ [MLT^−2])^0.5
=([M^2T^2])^0.5
So, RHS dimension = [MT]
So, LHS dimension is not equal to the dimension of RHS, so the equation is not correct.
Problem (c)
Solution:
The samples are given in the question are 2, 4, 6, 8, 10…40, in mV unit
So these are in Arithmetic progression with
First value, a= 2
Difference between consecutive numbers, d= 2 and
Number of values, n = 20
So, sum of these 20 voltage samples will be
S= n/2[2a+ (n-1) d]
S= 20/2[2*2+ (20-1)*2] =420 mV
So, the sum of these 20 voltage samples is 420 mV.
5 | P a g e

Problem (d)
6 | P a g e

Solution: (Minlos, 2000)
The digital chip is counting the sequence in Geometric Progression.
The nth value in G.P is given by
Tn= arn-1
Where, a= first value
r= common ration
n= number of terms
In the question
First value, a = 1024
Common ratio, r = 2
Number of terms, n = 9
So, 9th count of the chip is
T9= 1024*29-1 =1024*28 = 262144
So, the 9th count of the chip is 262144.
Problem (e)
Solution:
7 | P a g e

As per the question a electrical circuit having capacitor and resistor connected in series with DC supply is
having following parameters
Resistor, R = 1MΩ
Vs= 12 V
Vc= 2 V, when time, t=4 sec
So, from the equation to find the voltage across the capacitor
2=12(1-e-4/RC)
So, 1-e-4/RC=1/6
e-4/RC=1-1/6
-4/RC=ln(0.833)
RC=21.89
So, C = 21.89/106 = 21.89 μF
Problem (f)
Solution:
8 | P a g e

The signal used in the question is described by the formula
Where,
Vs is the instantaneous voltage
Amplitude = 6
Frequency, f=1MHz =10^6 Hz
Phase = -π/4
The instantaneous voltage is given as Vs=3 V
So using the equation
3=6sin(2 πft- π/4)
2 πft- π/4=sin-1(0.5)
Time , t= (sin-1(0.5)+ π/4)/ 2 πf
T=2.083333333 ×10^-7 =0.2 μsec
The test signal is simulated in MATLAB software and the figure is shown blow :
9 | P a g e

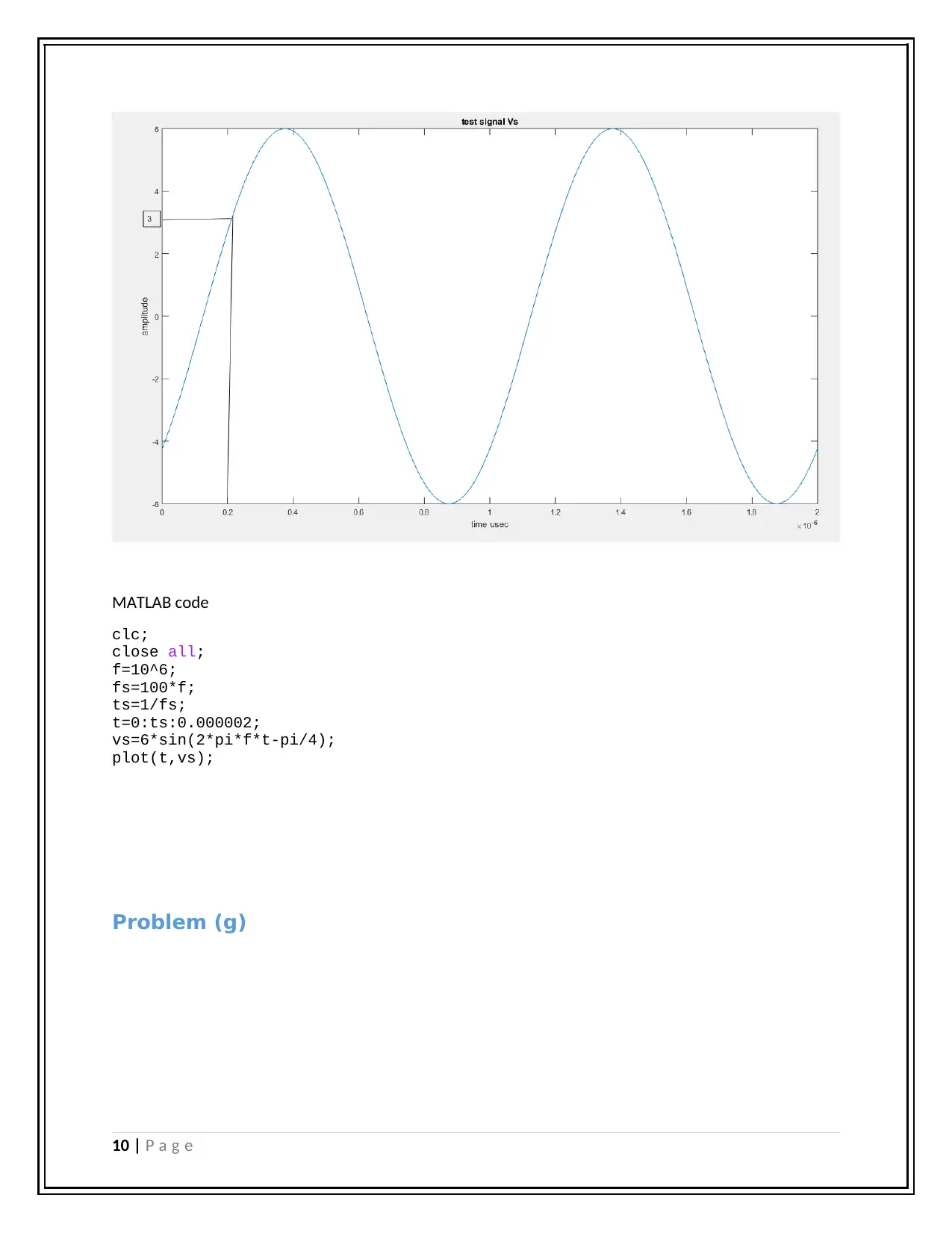
MATLAB code
clc;
close all;
f=10^6;
fs=100*f;
ts=1/fs;
t=0:ts:0.000002;
vs=6*sin(2*pi*f*t-pi/4);
plot(t,vs);
Problem (g)
10 | P a g e

Solution: (Thompson, 2016)
In this question the described equation for heavy power cable is given as
i) The value of y when x is 104
Y=60cosh(104/60)
Y=60.02745827748
ii) The value of x when y is 180
X=60*cosh-1(180/60)
X=6059.87840526312
Problem (h)
11 | P a g e

Solution: (Thompson, 2016)
The period (t) of the pendulum swing depends on
Mass attached =m
Length of the string =l
Acceleration due to gravity =g
Dimension of acceleration due to gravity, g = [LT^-2]
Dimension of l =[L]
Dimension of m=[M]
Let , time period
T ∝ la
T ∝ mb
T ∝ gc
Combining the above equation
T ∝ lambgc
T =K.lambgc
Where, k = constant
Writing above equation in dimensions
[T]= [L] ^a [M] ^b [LT^-2]^c
[M0L0T1]= [Mb][La][LcT-2c]
[M0L0T1]= [MbLa+cT-2c]
Equating the powers of M,L and T
12 | P a g e