Calculus 1A Assignment Solution: Question, Solution, and Analysis

This document provides a comprehensive solution to a Calculus 1A assignment. The assignment covers a range of calculus topics, including the application of product and quotient rules, the determination of absolute and local maxima and minima, and the analysis of function behavior through derivatives. The solutions include step-by-step explanations, application of the mean value theorem, the use of L'Hopital's Rule for indeterminate forms, and the sketching of curves based on given conditions. Furthermore, the assignment addresses integral calculus and proves a specific function's properties using the mean value theorem. The document offers a detailed breakdown of each problem, providing students with a thorough understanding of the concepts and methodologies involved.

300672 MATHEMATICS 1A
ASSIGNMENT – 4
STUDENT ID
[Pick the date]

Question 1
(a) y=cosh2( x ¿¿ 5) sinhx ¿
Let
f ( x )=cosh2( x ¿¿ 5)¿
g ( x )=sinhx
Apply product rule
( f . g ) ' =f ' . g+ f . g'
dy
dx = d
dx {cosh2 (x ¿¿ 5)}sinh ( x)+ d
dx {sinh (x )}cosh2( x¿¿ 5)… …(a)¿ ¿
= I + II
Solve I
I = d
dx {cosh2 (x ¿¿ 5)}¿
df ( u )
dx = df
du . du
dx
Let
cosh ( x ¿¿ 5)=u ¿
¿ d
du ( u2 ) . d
dx {cosh2 (x ¿¿ 5)}¿
¿ 2 u .sinh ( x¿ ¿5).5 x4 ¿
Substitute u=cosh ( x¿ ¿5)¿
1

¿ 2 cosh (x¿ ¿5). sinh(x ¿¿ 5). 5 x4 ¿¿
Simplify
I =10 x4 cosh ( x¿ ¿5) sinh(x ¿¿ 5)¿ ¿
Now,
II= d
dx {sinh (x )}
II=cosh ( x )
Now, substitute I and II in equation (a)
dy
dx =10 x4 cosh ( x ¿¿ 5)sinh( x ¿¿ 5)sinh ( x ) +cosh ( x ) cosh2 ( x¿ ¿5)¿ ¿ ¿
(b) y= sinh( x)
cos ( x )
Let
f =sinh ( x )
g=cos(x )
Applying the Quotient Rule
( f
g )'
= f ' . g−g' . f
g2
¿ d
dx ¿ ¿
¿ ¿ ¿
2

¿ cosh ( x ) .cos ( x ) +sin (x) sinh (x )
cos2 (x)
Question 2
d
dx ( tanh−1 x ) = 1
1−x2
Let
y=tanh−1 x
Or
x=tanh y
Differentiate both side w.r.t. x
d
dx tanh y = d
dx ( x )
sech2 y dy
dx =1
dy
dx = 1
sech2 y … … … … … ( 1 )
sech2 y=1−tanh2 y
dy
dx =
( 1
1−tanh2 y )
x=tanh y
3

dy
dx =
( 1
1−x2 )
Put
y=tanh−1 x
d
dx (tanh ¿¿−1 x)= ( 1
1−x2 ) ¿ Proved
Question 3
Absolute maximum and minimum value of f ( x)=?
f ( x )=4 x
2
7 + x
9
7 , closed interval [ −1 , 1 ]
Now,
f ( x )=4 x
2
7 + x
9
7
 Take first derivative of both the sides
f ' ( x ) =4 × ( 2
7 ) x
2
7 −1
+( 9
7 ) x
9
7 −1
f ' ( x ) = 8
7 x
−5
7 + 9
7 x
2
7
 Take f ' ( x )=0
f ' ( x )= 8
7 x
−5
7 + 9
7 x
2
7 =0
8
7 x
−5
7 + 9
7 x
2
7 =0
4

8
7 x
−5
7 =−9
7 x
2
7
8 x
−5
7 =−9 x
2
7
8
x
5
7
=−9 x
2
7
−8
9 =x
2
7 . x
5
7
−8
9 =x
7
7
x= (−8
9 )
Further,
f ( x )=4 x
2
7 + x
9
7
At x= (−8
9 )
f (−8
9 )= {4∗(−8
9 )2
7
}+ (−8
9 )9
7
f (−8
9 )=3.008
At x=0
f (0)=0 (critical point since f ' (0)is undefined)
5

At x = 1
f ( 1 ) =4 +1=5
At x = -1
f (−1 )=3
Therefore, function f(x) has absolute maximum value is 5 at x=1and absolute minimum value is
0 at x = 0.
Further, f has local maximum value is 3.008 at x = -8/9.
Question 4
f ( x )=ln( x2+ 4 x +8)
(a) F(x) is increasing or decreasing
First derivation of function f(x)
dy
dx = d
dx (ln ( x2 +4 x +8 ) )
¿ ( 1
x2 +4 x +8 ) d
dx ( x2 +4 x+8 )
¿ 1
x2 + 4 x+8 ( 2 x+4 )
¿ 2 x+ 4
x2 + 4 x+ 8
f ' ( x )= dy
dx = 2 x+ 4
x2 + 4 x+ 8
6

Put f’(x) = 0
2 x+ 4
x2 + 4 x+8 =0
2 x+ 4=0
x=−2
Sign of f’(x) would be given below:
f '> 0: f isincreasing on (−2 , ∞ )
f '< 0: f is decreasingon (−∞,−2 )
(b) Values x for which function f(x) would concave up and concave down
Second derivative of the function is shown below:
f ' ( x )= dy
dx = 2 x+ 4
x2 + 4 x+ 8
f '' ( x )= d2 y
d x2 = d
dx ( 2 x +4
x2+ 4 x +8 )
¿( x ¿¿ 2+ 4 x+ 8). d
dx ( 2 x + 4 ) − ( 2 x +4 ) . d
dx
( x ¿¿ 2+4 x +8)
(x ¿¿ 2+4 x+ 8)2 ¿ ¿ ¿
7

¿ ( x ¿¿ 2+4 x +8) ( 2 ) − ( 2 x+4 ) ( 2 x+ 4 )
( x ¿¿ 2+ 4 x +8)2 ¿ ¿
¿ (2 x¿ ¿2+8 x +16)− ( 4 x2 +16 x+16 )
(x ¿¿ 2+4 x +8)2 ¿ ¿
¿ 2 x2 +8 x+16−4 x2−16 x−16
(x ¿¿ 2+4 x+ 8)2 ¿
¿ −2 x2−8 x
(x ¿¿ 2+4 x +8)2 ¿
f ' ' ( x ) = −2 x (x+ 4)
(x ¿¿ 2+4 x +8)2 ¿
Now, put f ' ' ( x )=0
−2 x ( x+4 )
( x ¿¿ 2+4 x +8)2=0¿
−2 x ( x +4 )=0
x=0 ,−4
Sign of f’(x) would be given below:
f ' ' >0: concave up on (−∞ ,−4 ) ∪ (0 , ∞)
8

f '< 0: concave down on (−4 , 0 )
Question 5
f ' ( x )= dy
dx =(x −5)5 (x −6)6 ( x−7)7 ( x−8)8 ( x−9)9
F(x) has local maximum and minima
f ' ( x )= dy
dx = ( x−5 )5 ( x−6 )6 ( x−7 )7 ( x−8 )8 ( x−9 )9=0
( x−5 )5 ( x−6 )6 ( x−7 )7 ( x−8 )8 ( x−9 )9=0
x=5 , 6 , 7 , 8 , 9
The values of x would be termed as critical number of the given functions. These critical
numbers would be exists if the respective first derivation would be undefined at the values of x.
After determining the peaks and valley it would be fair to conclude that (4, -6) would be the local
minima. However, these two local extreme would be plugged in the original function. Hence, the
local maxima have been found as (-4, 7).
Question 6
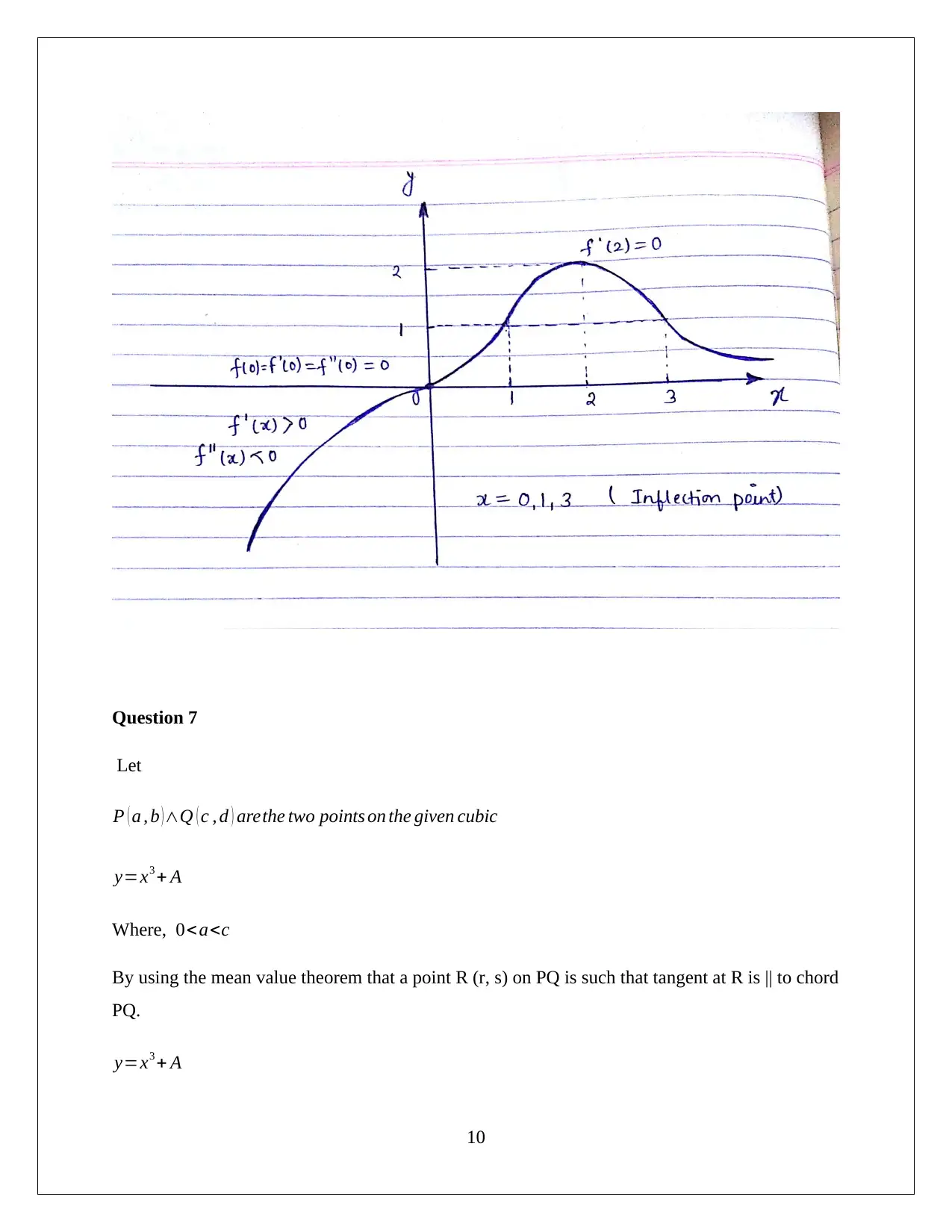
Sketch a curve as y = f(x) for the following conditions is represented below:
9

Question 7
Let
P ( a , b )∧Q ( c , d ) arethe two points on the given cubic
y=x3 + A
Where, 0<a<c
By using the mean value theorem that a point R (r, s) on PQ is such that tangent at R is || to chord
PQ.
y=x3 + A
10

dy
dx =3 x2
Let r ∈ ( a , c ) , a<r < c
Mean value theorem
dy
dx |x=r
= f ( c ) −f ( a )
c−a
f ( c ) =c3+ A
f ( a ) =a3+ A
dy
dx |x=r
=3 r2
Hence,
3 r2= ( c3 + A ) −(a3 + A )
c−a
3 r2= c3 + A−a3− A
c−a
3 r2= c3−a3
c−a
3 r2= ( c−a ) (c ¿¿ 2+ac +a2)
c−a ¿
3 r2=c2 +ac + a2
r2= c2 +ac +a2
3
r = √ ( c2+ ac+ a2
3 )
11