Building Mathematics Assignment: Detailed Solutions for Tasks 1 & 2
VerifiedAdded on 2023/02/01
|34
|6901
|67
Homework Assignment
AI Summary
This document presents a comprehensive solution to a Building Mathematics assignment, addressing two main tasks. Task 1 delves into various mathematical scenarios, including solving quadratic equations to determine dimensions, analyzing daily forfeits in contracts, and converting units for speed and fuel consumption. It also covers arithmetic and geometric progressions, including finding specific terms and calculating sums. Furthermore, it solves equations involving logarithmic and hyperbolic functions. Task 2 focuses on statistical analysis, involving the creation of histograms and cumulative frequency curves based on provided data distributions for January and July. The solution provides detailed calculations, graphical representations, and interpretations of the data, offering a complete understanding of the mathematical concepts involved.

Building Mathematics 1
BUILDING MATHEMATICS
Name
Course
Professor
University
City/state
Date
BUILDING MATHEMATICS
Name
Course
Professor
University
City/state
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Building Mathematics 2
Building Mathematics
Task 1
Scenario 1
1. Length and width
Area of rectangle = length x width
Let length be L m; width = (L – 3.2) m
Area = 26.5m2
L x (L – 3.2) = 26.5m2; L2 – 3.2L = 26.5m2
L2 – 3.2L – 26.5 = 0
The above equation is quadratic and can be solved using the quadratic formula
x=−b ± √ b2−4 ac
2 a as follows
L=− (−3.2 ) ± √(−3.2)²−(4 x 1 x−26.5)
2 x 1 = 3.2± √10.24 +106
2 = 3.2± √116.24
2 = 3.2± 10.7815
2
L = 6.9907 or -3.79075
Since length cannot be positive, it means that L = 6.99m
Width = L – 3.2m = 6.99m – 3.2m = 3.79m
2. Daily forfeit and original contract
Let the daily forfeit be x and the original contract be y
The amount the contract gets paid in case of late completion is expressed as p = y – xn; where p
= amount paid, y = original contract, x = daily forfeit and n = number of late days.
Forming the equations based on information given:
4250 = y – 5x …………………. (1)
2120 = y – 12x ……………..… (2)
Building Mathematics
Task 1
Scenario 1
1. Length and width
Area of rectangle = length x width
Let length be L m; width = (L – 3.2) m
Area = 26.5m2
L x (L – 3.2) = 26.5m2; L2 – 3.2L = 26.5m2
L2 – 3.2L – 26.5 = 0
The above equation is quadratic and can be solved using the quadratic formula
x=−b ± √ b2−4 ac
2 a as follows
L=− (−3.2 ) ± √(−3.2)²−(4 x 1 x−26.5)
2 x 1 = 3.2± √10.24 +106
2 = 3.2± √116.24
2 = 3.2± 10.7815
2
L = 6.9907 or -3.79075
Since length cannot be positive, it means that L = 6.99m
Width = L – 3.2m = 6.99m – 3.2m = 3.79m
2. Daily forfeit and original contract
Let the daily forfeit be x and the original contract be y
The amount the contract gets paid in case of late completion is expressed as p = y – xn; where p
= amount paid, y = original contract, x = daily forfeit and n = number of late days.
Forming the equations based on information given:
4250 = y – 5x …………………. (1)
2120 = y – 12x ……………..… (2)

Building Mathematics 3
These are simultaneous equations and can be solved simultaneously by subtracting the second
equation from the first one to give
2130 = 7x → x = £304.3
Substituting the value of x in the first equation gives
£4250 = y – (5*304.3)
£4250 = y – 1521.5; y = £5771.5
Therefore daily forfeit = £304.3 and original contract = £5,771.5
Scenario 2
a) Dimensional parameters
Speed in m/s
First is to convert the 65 miles into meters.
1 mile = 1760 yards
65 miles = 65 miles x 1760 yards
1 miles =114,400 yards
Then convert the yards into meters by multiplying by 0.91 to give
114,400 x 0.91 = 104,104m
So the speed is 104,104m/hour
The next step is to convert one hour into seconds by multiplying it by 3,600 to give
1hr x 3,600 sec/hr. = 3,600 seconds
Speed is 104,104m/3600 seconds meaning
3600 s = 104,104m
1 s = 1 x 104,104 m
3600 s =28.92m/s
Time taken
These are simultaneous equations and can be solved simultaneously by subtracting the second
equation from the first one to give
2130 = 7x → x = £304.3
Substituting the value of x in the first equation gives
£4250 = y – (5*304.3)
£4250 = y – 1521.5; y = £5771.5
Therefore daily forfeit = £304.3 and original contract = £5,771.5
Scenario 2
a) Dimensional parameters
Speed in m/s
First is to convert the 65 miles into meters.
1 mile = 1760 yards
65 miles = 65 miles x 1760 yards
1 miles =114,400 yards
Then convert the yards into meters by multiplying by 0.91 to give
114,400 x 0.91 = 104,104m
So the speed is 104,104m/hour
The next step is to convert one hour into seconds by multiplying it by 3,600 to give
1hr x 3,600 sec/hr. = 3,600 seconds
Speed is 104,104m/3600 seconds meaning
3600 s = 104,104m
1 s = 1 x 104,104 m
3600 s =28.92m/s
Time taken
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Building Mathematics 4
Time= Distance
Speed = 100 miles
65 miles/hour =1.5385 hours ≈1 hour 32 minutes
Fuel consumption
First is to convert 30 miles into kilometers by multiplying it by 1.61 to give
30 x 1.61 = 48.3 km
This means that the consumption is 48.3km/gallon. The consumption per kilometer is calculated
as follows:
48.3 km = 1 gallon
1 km = 1 x 1
48.3 =0.0207 gallons
Hence the consumption is 0.0207 gallons/kilometer.
The next step is to convert 0.0207 gallons into liters by multiplying it by 3.78 to give
0.0207 x 3.78 = 0.078246 liters
Thus the consumption is 0.078 liters/kilometer.
Fuel quantity
The fuel consumption rate is 0.078 liters/kilometer and the distance to be travelled is 100 miles.
The miles can be converted into kilometers by multiplying by 1.61 to give 100 x 1.61 = 161 km.
Therefore
1 km = 0.078 liters
161 km = 161km x 0.078 liters
1 km =12.6 liters
b) Units of lift
Lift = k x ρ x V2 x A
Where k = dimensionless, ρ = kg/m3, v = m/s and A = m2.
Time= Distance
Speed = 100 miles
65 miles/hour =1.5385 hours ≈1 hour 32 minutes
Fuel consumption
First is to convert 30 miles into kilometers by multiplying it by 1.61 to give
30 x 1.61 = 48.3 km
This means that the consumption is 48.3km/gallon. The consumption per kilometer is calculated
as follows:
48.3 km = 1 gallon
1 km = 1 x 1
48.3 =0.0207 gallons
Hence the consumption is 0.0207 gallons/kilometer.
The next step is to convert 0.0207 gallons into liters by multiplying it by 3.78 to give
0.0207 x 3.78 = 0.078246 liters
Thus the consumption is 0.078 liters/kilometer.
Fuel quantity
The fuel consumption rate is 0.078 liters/kilometer and the distance to be travelled is 100 miles.
The miles can be converted into kilometers by multiplying by 1.61 to give 100 x 1.61 = 161 km.
Therefore
1 km = 0.078 liters
161 km = 161km x 0.078 liters
1 km =12.6 liters
b) Units of lift
Lift = k x ρ x V2 x A
Where k = dimensionless, ρ = kg/m3, v = m/s and A = m2.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Building Mathematics 5
In terms of unit, lift = [kg/m3] x [m2/s2] x m2 = kgm/s2.
Scenario 3
1. Arithmetic Progression (AP) sequence
Sixth term
Since it is an AP sequence, the Tn term = a + (n – 1)d; where a = first term, n = number of terms
and d = common difference
In this case, a = b, n = 6 and d = −b
3
6th term = b + (6 – 1) −b
3 = b + −5 b
3 = b – 5 b
3 = −2 b
3
kth term
As aforementioned, kth term = a + (n – 1)d; a = b, n = k and d = and d =−b
3
kth term = b + (k – 1) −b
3 = b− bk
3 + b
3 = 4 b
3 −bk
3 =b
3 ( 4−k )
Value of b and sum of AP
The kth term is b
3 ( 4−k ). This means that the 20th term is b
3 ( 4−20 )=−16 b
3
Therefore −16 b
3 =15 → -16b = 45; b = -2.8125
Sum of first 20 terms = n
2 ( 2 a+ ( n−1 ) d ); where n = number of terms, a = first term and d =
common difference.
In this case, n = 20, a = b = -2.8125 and d=−b
3 =2.8125
3 =0.9375
Hence sum of first 20 terms = 20
2 (2 (−2.8125 ) + ( 20−1 ) (0.9375) )
In terms of unit, lift = [kg/m3] x [m2/s2] x m2 = kgm/s2.
Scenario 3
1. Arithmetic Progression (AP) sequence
Sixth term
Since it is an AP sequence, the Tn term = a + (n – 1)d; where a = first term, n = number of terms
and d = common difference
In this case, a = b, n = 6 and d = −b
3
6th term = b + (6 – 1) −b
3 = b + −5 b
3 = b – 5 b
3 = −2 b
3
kth term
As aforementioned, kth term = a + (n – 1)d; a = b, n = k and d = and d =−b
3
kth term = b + (k – 1) −b
3 = b− bk
3 + b
3 = 4 b
3 −bk
3 =b
3 ( 4−k )
Value of b and sum of AP
The kth term is b
3 ( 4−k ). This means that the 20th term is b
3 ( 4−20 )=−16 b
3
Therefore −16 b
3 =15 → -16b = 45; b = -2.8125
Sum of first 20 terms = n
2 ( 2 a+ ( n−1 ) d ); where n = number of terms, a = first term and d =
common difference.
In this case, n = 20, a = b = -2.8125 and d=−b
3 =2.8125
3 =0.9375
Hence sum of first 20 terms = 20
2 (2 (−2.8125 ) + ( 20−1 ) (0.9375) )

Building Mathematics 6
= 10(-5.625 + 19(0.9375))
= 10(-5.625 + 17.8125)
= 10(12.1875)
= 121.875
2. Geometric Progression (GP) sequence
20th term
For GP sequence, Tn = arn-1 where a = first term, r = common ratio and n = number of terms
In this case, a = 1, r = ½ and n = 20
20th = 1 x (½)20-1 = (½)19 = 0.000001907
Value of terms to infinity
Since the absolute value of r is less 1 and greater than 0, the sum of infinite terms of a GP series
is calculated using the formula S= a1
1−r ; where a1 = first term and r = common ratio (Hit
Bullseye, 2019).
In this case, a1 = 1 and r = ½
HenceS= 1
1− 1
2
= 1
1
2
=2
The reason why the sequence of geometric series of infinite terms tends to the value Sn= ∑
n=0
n → ∞
a rn
is because the common ratio r is 0<r<1 (not equal to -1, 0 or 1) hence the sequence show
exponential decay (Lumen, (n.d.)).
3. Equations for x
a) 2Log (3x) + Log (18x) = 27
= 10(-5.625 + 19(0.9375))
= 10(-5.625 + 17.8125)
= 10(12.1875)
= 121.875
2. Geometric Progression (GP) sequence
20th term
For GP sequence, Tn = arn-1 where a = first term, r = common ratio and n = number of terms
In this case, a = 1, r = ½ and n = 20
20th = 1 x (½)20-1 = (½)19 = 0.000001907
Value of terms to infinity
Since the absolute value of r is less 1 and greater than 0, the sum of infinite terms of a GP series
is calculated using the formula S= a1
1−r ; where a1 = first term and r = common ratio (Hit
Bullseye, 2019).
In this case, a1 = 1 and r = ½
HenceS= 1
1− 1
2
= 1
1
2
=2
The reason why the sequence of geometric series of infinite terms tends to the value Sn= ∑
n=0
n → ∞
a rn
is because the common ratio r is 0<r<1 (not equal to -1, 0 or 1) hence the sequence show
exponential decay (Lumen, (n.d.)).
3. Equations for x
a) 2Log (3x) + Log (18x) = 27
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Building Mathematics 7
Using quotient rule,
Log(3x)2 + Log (18x) = 27
Log(9x2) + Log (18x) = 27
Using product rule,
Log [(9x2) (18x)] = 27
Log 162x3 = 27
162x3 = 1027
x3= 1027
162 ; x=( 1027
162 )1
3
x= 109
5.4514 =183,440,402.7=183.44 x 106
b) 2LOGe(3x) + LOGe(18x) = 9
Removing the parentheses gives
2log e * 3x + log e * 18x = 9
Multiplying 2 by 3 in the first term gives
6log e * x + 18log e * x = 9
Adding the like terms log e * x on the left hand side gives
24log e * x = 9
Dividing both sides by 24 log e gives
x= 9
24 log e = 9
24 x 0.4342945 = 9
10.4231 =0.8635
c) Hyperbolic equations
i) Cosh(X) + Sinh(X) = 5
This is solved using the identity sinh ( x )=¿ −e−x +e x
2 ¿ and cosh ( x )=¿ e−x +ex
2 ¿
Using quotient rule,
Log(3x)2 + Log (18x) = 27
Log(9x2) + Log (18x) = 27
Using product rule,
Log [(9x2) (18x)] = 27
Log 162x3 = 27
162x3 = 1027
x3= 1027
162 ; x=( 1027
162 )1
3
x= 109
5.4514 =183,440,402.7=183.44 x 106
b) 2LOGe(3x) + LOGe(18x) = 9
Removing the parentheses gives
2log e * 3x + log e * 18x = 9
Multiplying 2 by 3 in the first term gives
6log e * x + 18log e * x = 9
Adding the like terms log e * x on the left hand side gives
24log e * x = 9
Dividing both sides by 24 log e gives
x= 9
24 log e = 9
24 x 0.4342945 = 9
10.4231 =0.8635
c) Hyperbolic equations
i) Cosh(X) + Sinh(X) = 5
This is solved using the identity sinh ( x )=¿ −e−x +e x
2 ¿ and cosh ( x )=¿ e−x +ex
2 ¿
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Building Mathematics 8
Substituting these identities in the equation gives
e−x +ex
2 + −e−x+ ex
2 =5
e−x
2 + e x
2 +−e−x
2 + ex
2 =5
ex = 5
log ex = log 5
xlog e = log 5
x= log 5
log e = 0.69897
0.4342945 =1.60944
Alternatively, ex = 5 means x = ln 5 = 1.60944
ii) Cosh(2Y) – Sinh(2Y) = 3
This is solved using the identity sinh ( y )=¿ −e− y +e y
2 ¿ and cosh ( y )=¿ e− y +e y
2 ¿
Substituting these identities in the equation gives
e−2 y+ e2 y
2 −−e−2 y +e2 y
2 =3
e−2 y
2 + e2 y
2 − (−e−2 y
2 + e2 y
2 )=3
e−2 y
2 + e2 y
2 + e−2 y
2 − e2 y
2 =3
e−2 y
2 + e−2 y
2 =3
e-2y = 3
-2y = ln 3
y=−1
2 ln 3 = -0.54931
Substituting these identities in the equation gives
e−x +ex
2 + −e−x+ ex
2 =5
e−x
2 + e x
2 +−e−x
2 + ex
2 =5
ex = 5
log ex = log 5
xlog e = log 5
x= log 5
log e = 0.69897
0.4342945 =1.60944
Alternatively, ex = 5 means x = ln 5 = 1.60944
ii) Cosh(2Y) – Sinh(2Y) = 3
This is solved using the identity sinh ( y )=¿ −e− y +e y
2 ¿ and cosh ( y )=¿ e− y +e y
2 ¿
Substituting these identities in the equation gives
e−2 y+ e2 y
2 −−e−2 y +e2 y
2 =3
e−2 y
2 + e2 y
2 − (−e−2 y
2 + e2 y
2 )=3
e−2 y
2 + e2 y
2 + e−2 y
2 − e2 y
2 =3
e−2 y
2 + e−2 y
2 =3
e-2y = 3
-2y = ln 3
y=−1
2 ln 3 = -0.54931

Building Mathematics 9
iii) Cosh(K) * Sinh(K) = 2
This is solved using the identity sinh ( K )=¿ −e−k + ek
2 ¿ and cosh ( K )=¿ e−k +ek
2 ¿
Substituting these identities in the equation gives
( e−k +ek
2 )∗(−e−k +ek
2 )=2
( e−k
2 + ek
2 )∗( −e−k
2 + ek
2 )=2
Opening the brackets gives
−e−2 k
4 + e0
4 − e0
4 + e2 k
4 =2
Simplifying e2k – e-2k = 8
This can also be written as e2 k− 1
e2 k =8
Let e2k be m
Substituting this in the above equation gives: m −1
m =8 (multiplying every term by m)
m2 – 1 = 8m; m2 – 8m – 1 = 0 – this is a quadratic equation and is solved using the quadratic
formula x=−b ± √ b2−4 ac
2 a as follows
m=− (−8 ) ± √(−8)²−(4 x 1 x−1)
2 x 1 = 8 ± √ 64+ 4
2 = 8 ± √68
2 = 8 ± 8.246
2
m = 8.123 or -0.123
Therefore e2k = 8.123 or -0.123
Solving by logarithm
Log e2k = log 8.123
iii) Cosh(K) * Sinh(K) = 2
This is solved using the identity sinh ( K )=¿ −e−k + ek
2 ¿ and cosh ( K )=¿ e−k +ek
2 ¿
Substituting these identities in the equation gives
( e−k +ek
2 )∗(−e−k +ek
2 )=2
( e−k
2 + ek
2 )∗( −e−k
2 + ek
2 )=2
Opening the brackets gives
−e−2 k
4 + e0
4 − e0
4 + e2 k
4 =2
Simplifying e2k – e-2k = 8
This can also be written as e2 k− 1
e2 k =8
Let e2k be m
Substituting this in the above equation gives: m −1
m =8 (multiplying every term by m)
m2 – 1 = 8m; m2 – 8m – 1 = 0 – this is a quadratic equation and is solved using the quadratic
formula x=−b ± √ b2−4 ac
2 a as follows
m=− (−8 ) ± √(−8)²−(4 x 1 x−1)
2 x 1 = 8 ± √ 64+ 4
2 = 8 ± √68
2 = 8 ± 8.246
2
m = 8.123 or -0.123
Therefore e2k = 8.123 or -0.123
Solving by logarithm
Log e2k = log 8.123
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Building Mathematics 10
2klog e = log 8.123
k = log 8.123
2 log e =0.909716
0.86859 =1.0473
iv) Cosh(M)/Sinh(M) = 2
This is also solved using the identities sinh ( M ) =¿ −e−m +em
2 ¿ and cosh ( M )=¿ e−m+ em
2 ¿
Substituting these identities in the equation gives
( e−m +em
2 )
(−e−m +em
2 )=2
e−m+ em
2 ∗2
−e−¿m + em =2¿
e-m + em = -2e-m + 2em
e-m + 2e-m + em – 2em = 0
3e-m – em = 0
This can also be written as:
3
em −em =0
Let em = x
3
x −x=0 (Multiplying each term by x)
3 – x2 = 0
x2 = 3
x = √3
Hence em = √3
2klog e = log 8.123
k = log 8.123
2 log e =0.909716
0.86859 =1.0473
iv) Cosh(M)/Sinh(M) = 2
This is also solved using the identities sinh ( M ) =¿ −e−m +em
2 ¿ and cosh ( M )=¿ e−m+ em
2 ¿
Substituting these identities in the equation gives
( e−m +em
2 )
(−e−m +em
2 )=2
e−m+ em
2 ∗2
−e−¿m + em =2¿
e-m + em = -2e-m + 2em
e-m + 2e-m + em – 2em = 0
3e-m – em = 0
This can also be written as:
3
em −em =0
Let em = x
3
x −x=0 (Multiplying each term by x)
3 – x2 = 0
x2 = 3
x = √3
Hence em = √3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Building Mathematics 11
M = ln √3
M = ln (3)1/2
M = ½ ln (3)
Task 2
Scenario 1
Table 1: January distribution
Class
interval
x Frequency, f CF d = x-A fd f(x−x ¿ ²
0-5 2.5 27 27 -7.5 -202.5 2335.23
5-10 7.5 38 65 -2.5 -95 702.62
10-15 12.5 40 105 2.5 100 19.6
15-20 17.5 22 127 7.5 165 714.78
20-30 25 13 140 15 195 2265.12
30-40 35 4 144 25 100 2152.96
∑ f =144 ∑ fd =262.5 ∑ f ( x−x )2=¿ 8190.31 ¿
Table 2: July distribution
Class
interval
x Frequency, f CF d = x-A fd f( x−x ¿ ²
0-5 2.5 22 22 -7.5 -165 2566.08
5-10 7.5 39 61 -2.5 -97.5 1311.96
10-15 12.5 69 130 2.5 172.5 44.16
15-20 17.5 41 171 7.5 307.5 723.24
20-30 25 20 191 15 300 2737.8
30-40 35 5 196 25 125 2354.45
∑ fd=642.5 ∑ f ( x−x ) 2=¿ 9737.69 ¿
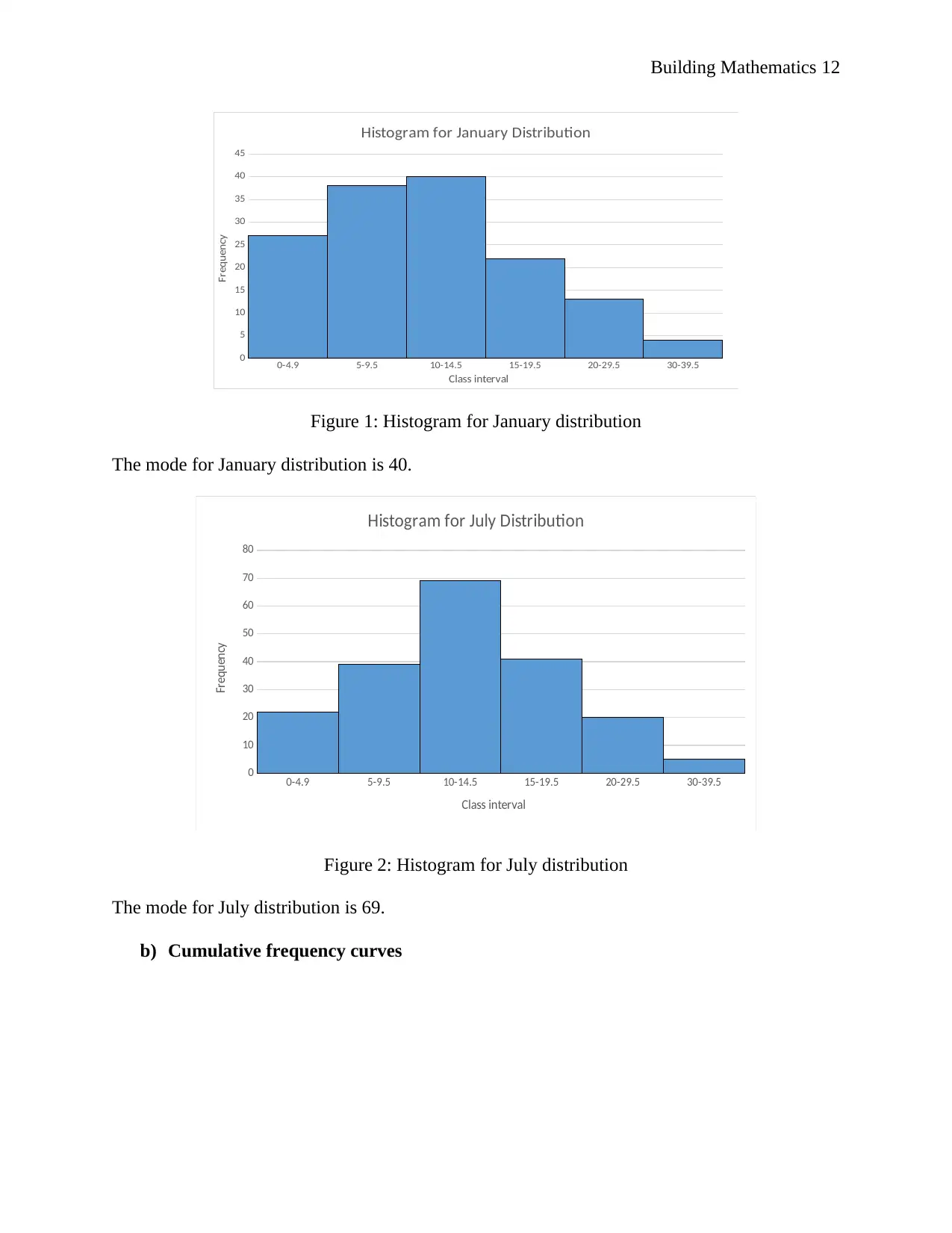
a) Histograms
A histogram is a bar graph of frequency against lower limits. The histograms of the distributions
are provided in Figure 1 and 2 below
M = ln √3
M = ln (3)1/2
M = ½ ln (3)
Task 2
Scenario 1
Table 1: January distribution
Class
interval
x Frequency, f CF d = x-A fd f(x−x ¿ ²
0-5 2.5 27 27 -7.5 -202.5 2335.23
5-10 7.5 38 65 -2.5 -95 702.62
10-15 12.5 40 105 2.5 100 19.6
15-20 17.5 22 127 7.5 165 714.78
20-30 25 13 140 15 195 2265.12
30-40 35 4 144 25 100 2152.96
∑ f =144 ∑ fd =262.5 ∑ f ( x−x )2=¿ 8190.31 ¿
Table 2: July distribution
Class
interval
x Frequency, f CF d = x-A fd f( x−x ¿ ²
0-5 2.5 22 22 -7.5 -165 2566.08
5-10 7.5 39 61 -2.5 -97.5 1311.96
10-15 12.5 69 130 2.5 172.5 44.16
15-20 17.5 41 171 7.5 307.5 723.24
20-30 25 20 191 15 300 2737.8
30-40 35 5 196 25 125 2354.45
∑ fd=642.5 ∑ f ( x−x ) 2=¿ 9737.69 ¿
a) Histograms
A histogram is a bar graph of frequency against lower limits. The histograms of the distributions
are provided in Figure 1 and 2 below
Building Mathematics 12
0-4.9 5-9.5 10-14.5 15-19.5 20-29.5 30-39.5
0
5
10
15
20
25
30
35
40
45
Histogram for January Distribution
Class interval
Frequency
Figure 1: Histogram for January distribution
The mode for January distribution is 40.
0-4.9 5-9.5 10-14.5 15-19.5 20-29.5 30-39.5
0
10
20
30
40
50
60
70
80
Histogram for July Distribution
Class interval
Frequency
Figure 2: Histogram for July distribution
The mode for July distribution is 69.
b) Cumulative frequency curves
0-4.9 5-9.5 10-14.5 15-19.5 20-29.5 30-39.5
0
5
10
15
20
25
30
35
40
45
Histogram for January Distribution
Class interval
Frequency
Figure 1: Histogram for January distribution
The mode for January distribution is 40.
0-4.9 5-9.5 10-14.5 15-19.5 20-29.5 30-39.5
0
10
20
30
40
50
60
70
80
Histogram for July Distribution
Class interval
Frequency
Figure 2: Histogram for July distribution
The mode for July distribution is 69.
b) Cumulative frequency curves
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 34
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



