Maths Assignment: Trigonometry, Algebra, Statistics, Calculus

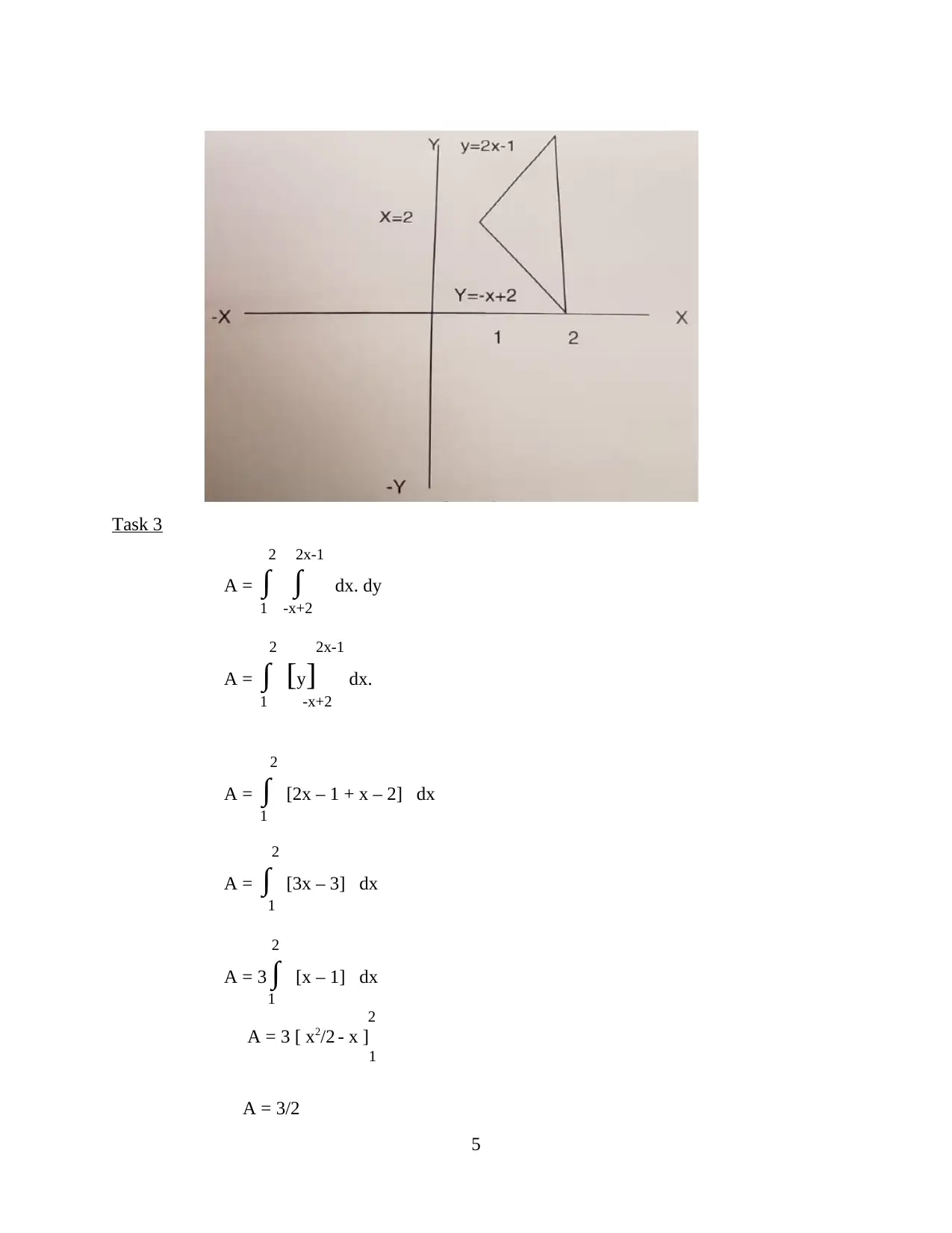
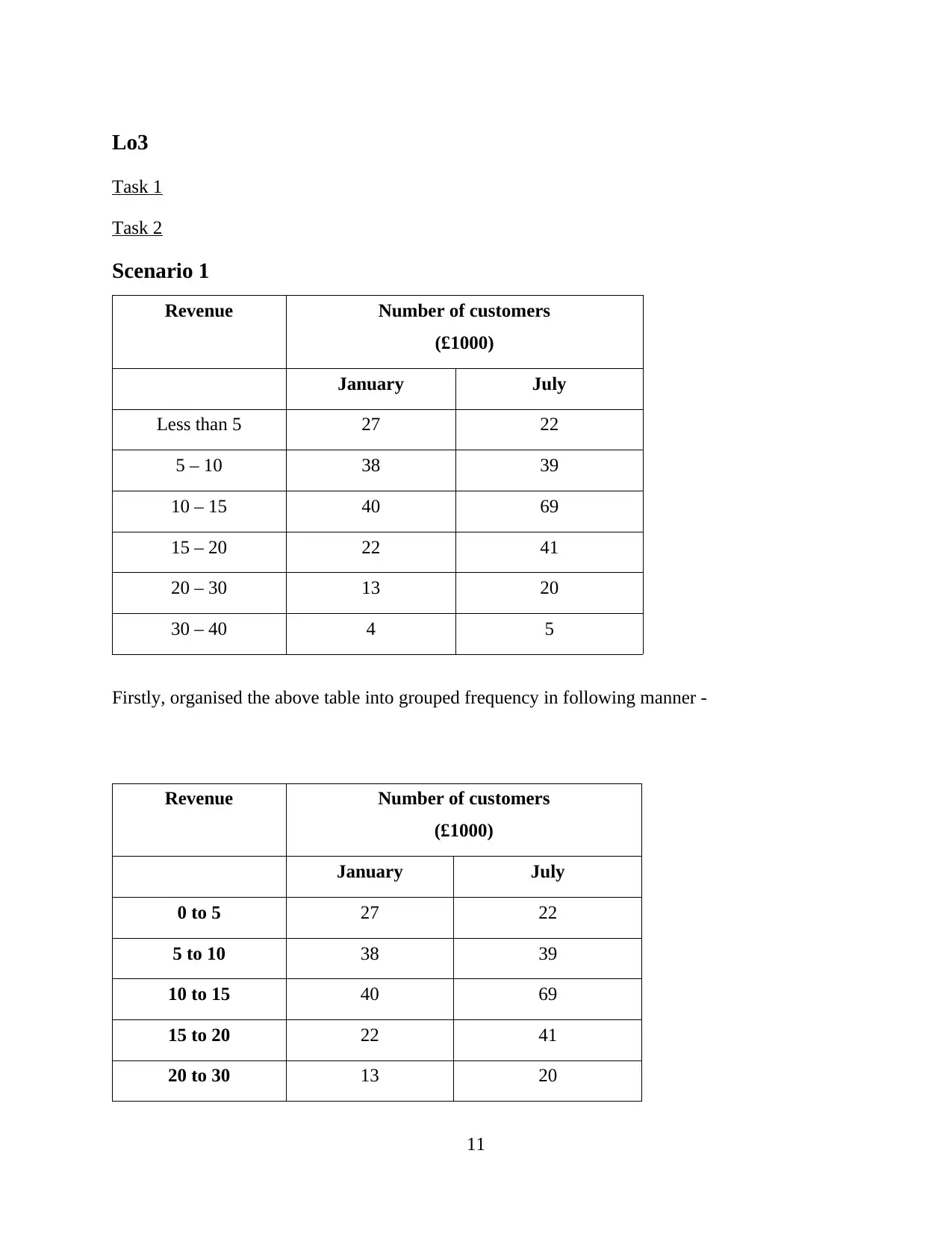
This mathematics assignment solution encompasses a range of topics including trigonometry, algebra, calculus, and statistics, with applications in engineering concepts. Task 1 delves into trigonometric calculations, applying the Law of Sines to solve for sides and angles in a triangle. Task 2 explores trigonometric functions, including amplitude, period, and proving trigonometric identities, along with solving exponential equations. Task 3 covers integration, calculating areas and moments. Furthermore, the assignment includes problems on chainage and offsets using trapezoidal and Simpson's rules, along with logarithmic equations and matrix determinants. The final tasks involve statistical analysis, including frequency distributions, histograms, mode calculations, and linear regression to model relationships between variables. The solutions provide step-by-step calculations and explanations for each problem.

Maths

TASK 1
1.1 In ∆ABC, A = 530 , B = 610 and length of a = 12.6cm
So, b and c can be calculated by following way -
using law of sine -
a = b = c
Sin A Sin B Sin C
from, given ∆ -
A + B + C = 180
530 + 610 + C = 180
C = 660
therefore,
12.6 = b = c
Sin 530 Sin 610 Sin 660
12.6 = b = c
0.79 0.87 0.91
so, b = 13.87 cm
while, c = 14.51 cm
B
Here, perpendicular = 15 unit
hypotenuse = 17 unit
then, base can be determined by -

b2 = h2 – p2
= 172 – 152
= 289 – 225
= 64
or, b = √64 = 8 unit
Sin Ø = perpendicular / hypotenuse
Sin Ø = 15/17 unit
TASK 2
a) Amplitude and period of waveform
y = 4 cos(2θ + 450)
Amplitude of given equation is 4
and, period of above equation = 2 π / 2θ = π / θ
a) Amplitude and period of waveform
y = 6 sin (t - 300)
Amplitude of given equation is 6
and, period of above equation = 2 π / t
c) To Prove -
sin 2 x (sec x + cosec x) = 1 + tan x
cosx tanx
taking LHS side of given equation-
sin 2 x (sec x + cosec x)
cosx tanx
» sin 2 x (1/cosx + 1/sinx )
cox . sinx/cosx
» sin 2 x (sin x + cos x)/ sinx cosx
cox . sinx/cosx
» sinx + cos x
cox
» tanx + 1 = RHS Hence Proved
2

Task 2
Given Indical equation -
x2 (2x-3)
(32) + (3) = 27
2x2 (2x-3) 3
(3) + (3) = 3
Using exponent rules,
2x2 + 2x – 3 3
3 = 3
3

When base of equation is same, then power is also equal -
therefore,
2x2 + 2x – 3 = 3
or, 2x2 + 2x – 6 = 0
or, x2 + x – 3 = 0
Solving this quadratic equation -
x = -b ± √ (b2 – 4ac)
2a
x = -1 ± √ (12 – 4 x 1 x -3)
2 x 1
= -1 ±√13
3
therefore, x = (-1 + √13)/ 2 or, (-1 - √13)/ 2
4

Task 3
2 2x-1
A = ∫ ∫ dx. dy
1 -x+2
2 2x-1
A = ∫ [y] dx.
1 -x+2
2
A = ∫ [2x – 1 + x – 2] dx
1
2
A = ∫ [3x – 3] dx
1
2
A = 3 ∫ [x – 1] dx
1
2
A = 3 [ x2/2 - x ]1
A = 3/2
5

2 2x-1
My = ∫ ∫ x. dy. dx
1 -x+2
2 2x-1
My = ∫ [x. y]. dx
1 -x+2
2
My = ∫ [x. (2x -1 + x – 2]. dx
1
2
My = 3. ∫ [x2 - x]. dx
1
or, 2
My = 3 [x3/3 – x2/2]1
= 5/6
6

2 2x-1
Mx = ∫ ∫ y. dy. dx
1 -x+2
2 2x-1
Mx = ∫ [ y2/2]. dx
1 -x+2
2
Mx = ½ ∫ [ (2x-1)2 - (-x+2)2 ]. dx
1
2
Mx = 3/2 ∫ [x2 - 1]. dx
1
or, 2
Mx = 3/2 [x3/3 – x]1
= 2
7

Task 1
1.
Chainage Offset 'm'
0 3.6
25 5
50 6.5
75 7.5
100 7.3
125 6
150 4
Common distance d = 25m
Area
(i) Using Trapezoidal Rule-
b
∫ f(x). dx = (b -a) [f(a) + f(b)]
a 2
From the above mentioned table, x varies from 0 to 150 -
150
q = ∫ f(x). dx
0
d = 25m
therefore,
150
A = ∫ f(x). dx ≈ 25/2 ( 3.6+ 5.0 + 6.5 + 7.5 + 7.3 + 6.0 + 4.0)
0
≈ 25/2 (39.9)
≈ 498.75
(ii) Using Simpson's Rule
b
8

∫f(x). dx = (b -a) [(first observation + last observation) + 4 (sum of even observation) + 2 (sum of others)]
a 3
therefore,
150
A = ∫ f(x). dx
0
A ≈ (25/3) [ (3.6+4.0) + 2 (5.0+7.5+6.0) + 4 (6.5 + 7.3) ]
≈ (25/3) [ (7.6) + 2 (18.5) + 4 (13.8) ]
≈ (25/3) [ (3.6+4.0) + 2 (5.0+7.5+6.0) + 4 (6.5 + 7.3) ]
≈ 831.66
2.
(a) 2 log9 (√x) - log9 (6x – 1) = 0
using logarithmic rules i.e. log (a/b) = log a – log b
so,
2 log9 (√x / (6x- 1) = 0
√x / (6x- 1) = 0
√x = (6x- 1)
x = (6x – 1)2
or, x = 36 x2 – 12x + 1
or, 36 x2 – 13x + 1 = 0
or, (9x – 1) (4x + 1) = 0
or, x = 1/9 ; -1/4
3 Determinant of matrix
1 2 3
0 -4 1
0 3 -1
Solution Using determinant formula of 3 x 3 matrix as
A = a11 a12 a13
9

a21 a22 a23
a31 a31 a33
then, determinant of any 3x3 matrix can be calculated by using the given formula
A = a11 ( a22 x a33 – a23 x a31) – a12 ( a21 x a33 – a23 x a31) +a13 (a21 x a31 - a22 x a31)
Using this formula, to find determinant of given matrix is given by can be calculated as
1 2 3
A = 0 -4 1
0 3 -1
then, determinant of A = [ 1 ( -4 x -1 – 1 x3) - 2 ( 0 x -1 – 1 x 0 ) + 3 (0 x 3 – 1 x 0) ]
= [ 1 (4 – 3) – 2 ( 0 – 0) + 3 ( 0 – 0 )]
= 1
10

Lo3
Task 1
Task 2
Scenario 1
Revenue Number of customers
(£1000)
January July
Less than 5 27 22
5 – 10 38 39
10 – 15 40 69
15 – 20 22 41
20 – 30 13 20
30 – 40 4 5
Firstly, organised the above table into grouped frequency in following manner -
Revenue Number of customers
(£1000)
January July
0 to 5 27 22
5 to 10 38 39
10 to 15 40 69
15 to 20 22 41
20 to 30 13 20
11