Open University MU123 EMA Assignment: Comprehensive Solutions

This document contains a comprehensive solution to the MU123 EMA assignment, focusing on Discovering Mathematics. The assignment covers a range of mathematical concepts, including study plans, data analysis (discrete data, measures of location and spread, boxplots), graphical representations (histograms), linear equations, parabolas, quadratic equations, geometric problems (Pythagorean theorem, cosine rule), and linear and exponential models. Solutions are provided with step-by-step calculations, explanations, and graphical representations where appropriate. The assignment delves into topics such as calculating gradients, intercepts, determining the intersection of lines, analyzing data variability, and interpreting the results of mathematical models.

DISCOVERING
MATHEMATICS
MU123 EMA
Student Name
[Pick the date]

Question 1
One change that I intend to make in my study plan in the future would be to practice the concepts
learnt in class on the very same day. This is because in the class, there were a number of topics
which seemed qutie straight forward but I faced significant problems when I did the same some
days later. Hence, in order to avoid this problem and to enhance learning, I would like to rectify
this error the next time around.
Question 2
Katie’s and Rebecca’s number of steps over a period of two week is highlighted below:
(a) (i) The respective numerical summary is shown below:
(ii) The given data is discrete data since the data cannot be in decimals.
1

(iii) The two measures of location to decide who has higher number of steps on average are
“Median and Mean.” Based on the above table, it can be seen that mean and median are higher
for Rebecca and therefore, Rebecca has greater number of steps on average.
(iv) The measures of spread to decide who has higher variability in terms of number of steps are
“Standard deviation, Inter-quartile range, Range.” All the three measures are higher for Rebecca.
Therefore, Rebecca’s number of steps is higher than Katie’s number of steps.
(b) (i) Boxplots
 Boxplot for variable Katie’s number of steps over two week period
 Boxplot for variable Rebecca’s number of steps over two week period
2

(ii) The box plot for Rebecca is clearly asymmetric as highlighted from the unequal distance
between Q1 and median & median and Q3. This implies that the spread of the data would be
more and also there would be potential presence of outliers in the data.
(iii) (1) This claim is false since from the box-plot of Katie, it is apparent that Q3 or 75th
percentile for the given data fall is 10.753 steps.
(2) This statement is false since the 8946 is marginally greater than the median of 8945.5 steps
which clearly implies that days when Katie did more than 8946 would be less than 50% while
days when she did less than 8946 steps would be slightly in excess of 50%.
(c) Running data over three weeks are highlighted below:
3

Based on the maximum running distance covered by Daniel and Andrew, it can be seen that
maximum running distance covered by Daniel is 8678 meter. In figure A, the maximum distance
cover of 8678 is possible and hence, figure A is the histogram represents the running distance
covered by Daniel. In figure B, the maximum distance is in excess of 10,000 steps.
Question 3
(a) Straight line passes through (1, -1) and (-2, 8)
(i) Gradient of the line
m= 8− (−1 )
−2− ( 1 ) = 9
−3 =−3
(ii) Equation of line
¿
y +1=−3 x +3
y=−3 x +2
4

(iii) The value of x-intercept
Value of x intercept would be at y = 0.
0=−3 x+ 2
x= 2
3 =0.667
(b) Point (3, -11) lie on the straight line =?
If the point satisfies the equation then the point lies on the line.
y=−3 x +2
LHS
y=−11
RHS
¿− ( 3∗3 ) +2=−7
The point (3, -11) does not lie on the line.
(c) Coordinates of point where the lines intersect.
9 x− y =2
−6 x +4 y=7
Here,
9 x− y =2
x= 2+ y
9
5

Put in equation 2
−6 x +4 y=7
−6 ( 2+ y
9 )+ 4 y =7
y= 5
2
Hence,
x=
2+( 5
2 )
9 = 1
2
Therefore, the point at which the lines would intersect is ( 1
2 , 5
2 ).
(d) Equation of parabola
y=−0.15 x2 + x +0.5
(i) The value of y-intercept
y=0.5
The value of y –intercept is 0.5.
(ii) (1) Coordinates of point where line x = 4 meets the parabola
y=−0.15 x2 + x +0.5
y=−0.15(4)2+ 4+0.5
6

y=2.1
Coordinates of point where line x = 4 meets the parabola is (4, 2.1).
(2) From the above, it is apparent that the y coordinate is 2.1m and hence the water would flow
above the sculpture with a height of 1.8m which is placed at the horizontal distance of 4 m from
the fountain.
(iii) (1) The value of x-intercept
y=−0.15 x2 + x +0.5
The value of x –intercept at which y=0.
0=−0.15 x2+ x +0.5
−0.15 x2+ x +0.5=0
−15 x2+100 x +50=0
x=−100 ± √(100)2−4 ( −15 )∗50
2∗(−15)
x=− √130+10
3 , 10+ √130
3
The value of x –intercept is (− √13010
3 , 10+ √130
3 ).
(2) Requisite distance = 10+ √130
3
Question 4
(a) (i) x−5=4 x +10
7

x−4 x=10+5
−3 x=15
x= 15
−3 =−5
(ii) 12−2 ( x+ 3
4 )=3
2 x
12−2 x− 3
2 = 3
2 x
−2 x−3
2 x=−21
2
−7
2 x=−21
2
x=3
(iii) 3 x
x−5 + 1
x +1 =3
3 x ( x+ 1 )+1 ( x−5 )
( x−5 ) ( x +1 ) =3
3 x2 +3 x+ x−5
x2 +x−5 x−5 =3
3 x2 +4 x−5
x2−4 x−5 =3
3 x2+4 x−5=3 ( x2−4 x −5 )
3 x2+4 x−5=3 x2 −12 x−15
8

16 x=−10
x=−5
8
(b) Factors and solution of equation
2 x2 +4 x−70=0
Factors
¿ 2 ( x2+2 x−35 )
¿ 2 { x2+ ( 7 x−5 x ) −35 }
¿ 2 ( x2+7 x−5 x−35 )
¿ 2 { x ( x +7 ) −5 ( x +7 ) }
¿ 2(x +7)( x−5)
Hence, the factors of the equation is 2 ( x+7 ) ( x−5 ) .
Solution of equation
2 x2 +4 x−70=0
2 ( x+7 ) ( x−5 )=0
x +7=0 , x=−7
x−5=0 , x=5
Solution of the equation is 5, -7.
(c) (i) Rearrange in terms of b subject
2 a=b−c (b
3 −4 )
9

2 a=b−c (b−12
3 )
2 a=b− ( bc−12 c
3 )
2 a=3 b−bc +12 c
3
6 a=3 b−bc+ 12c
6 a−12 c=b ( 3−c )
b= 6 a−12 c
( 3−c )
(ii) The two mistakes are highlighted below:
Question 5
The figure is shown below:
10

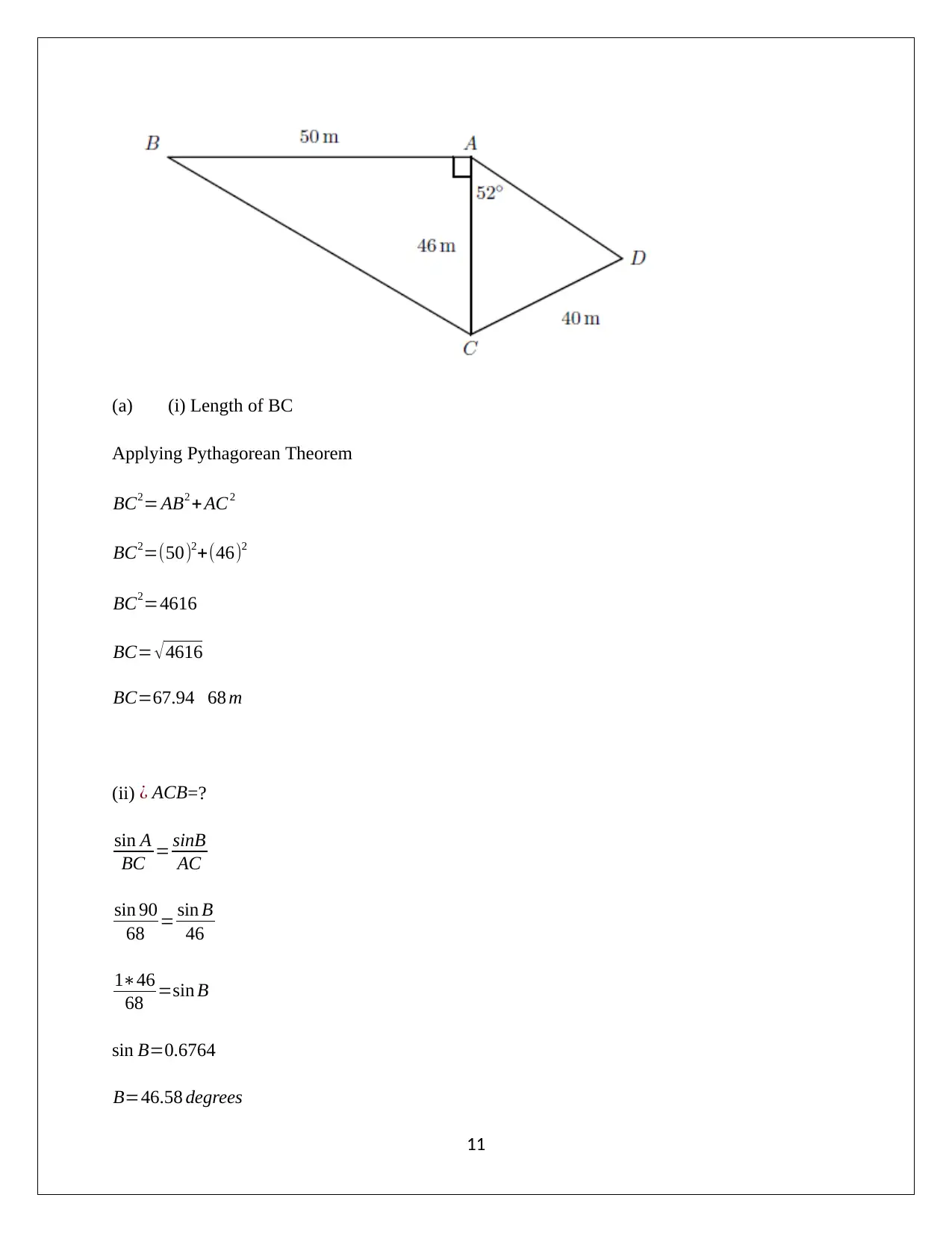
(a) (i) Length of BC
Applying Pythagorean Theorem
BC2= AB2 +AC 2
BC2=(50)2+(46)2
BC2=4616
BC= √4616
BC=67.94 68 m
(ii) ¿ ACB=?
sin A
BC = sinB
AC
sin 90
68 = sin B
46
1∗46
68 =sin B
sin B=0.6764
B=46.58 degrees
11