Mathematics for Computing: Assignment Solution - Discrete Structures

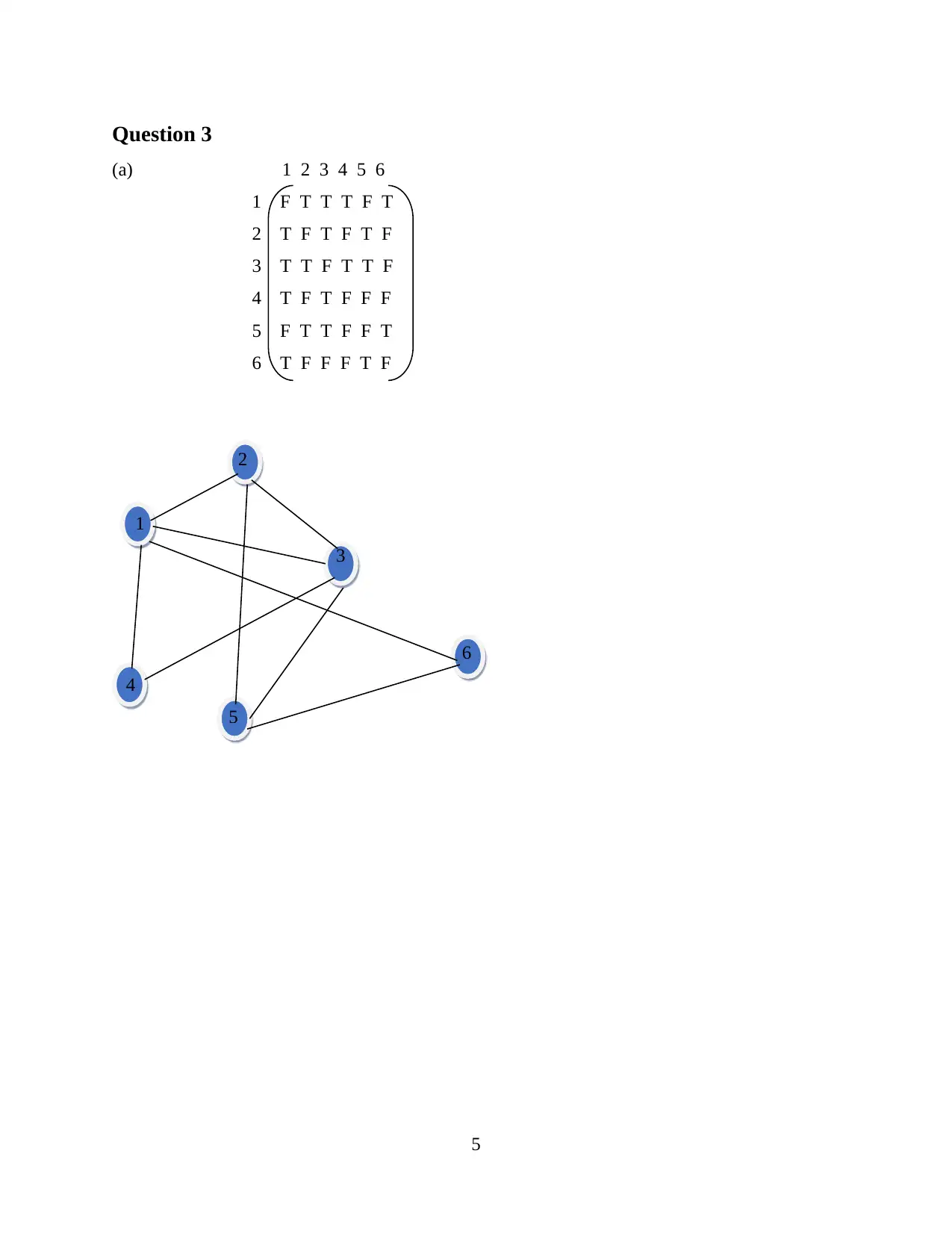
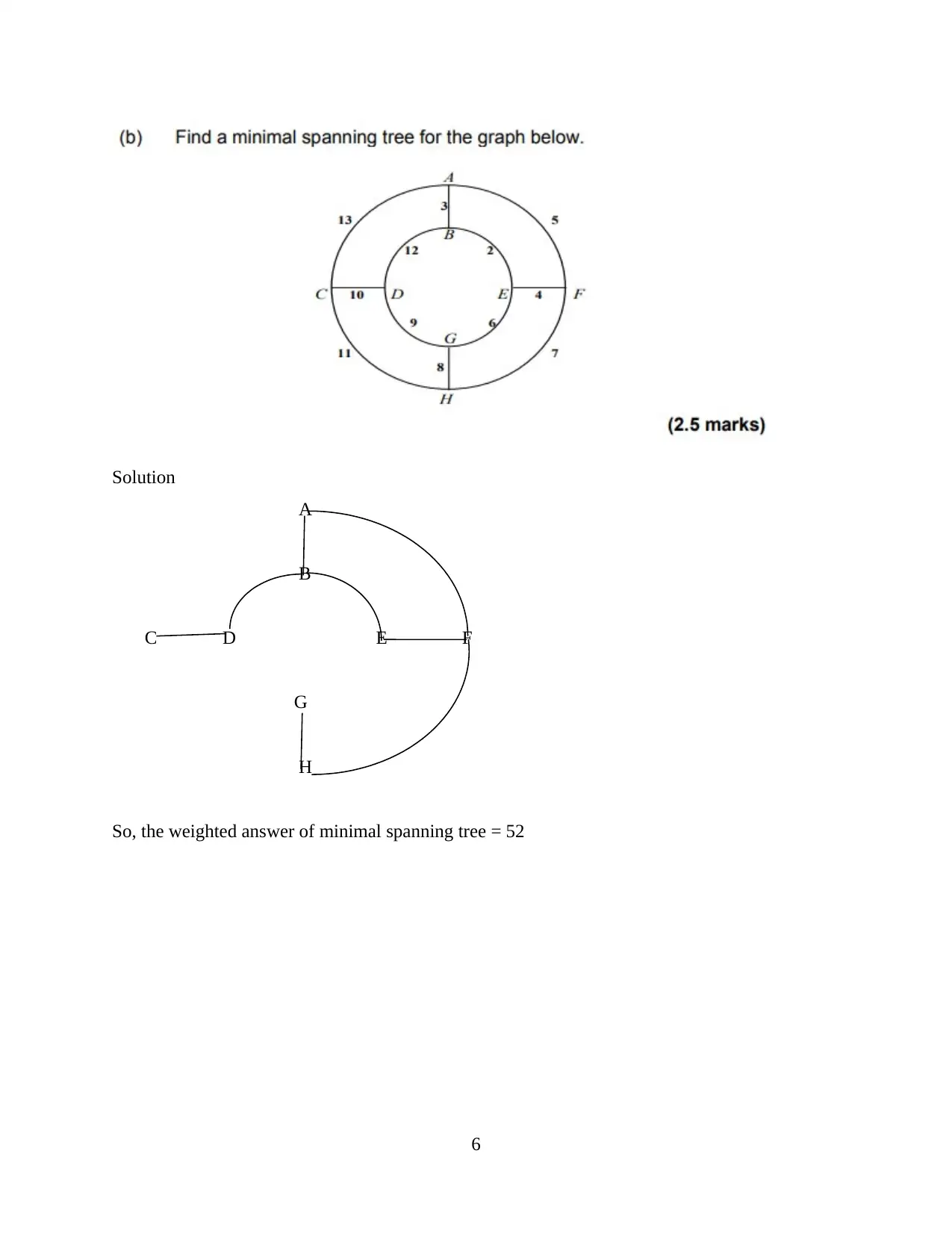
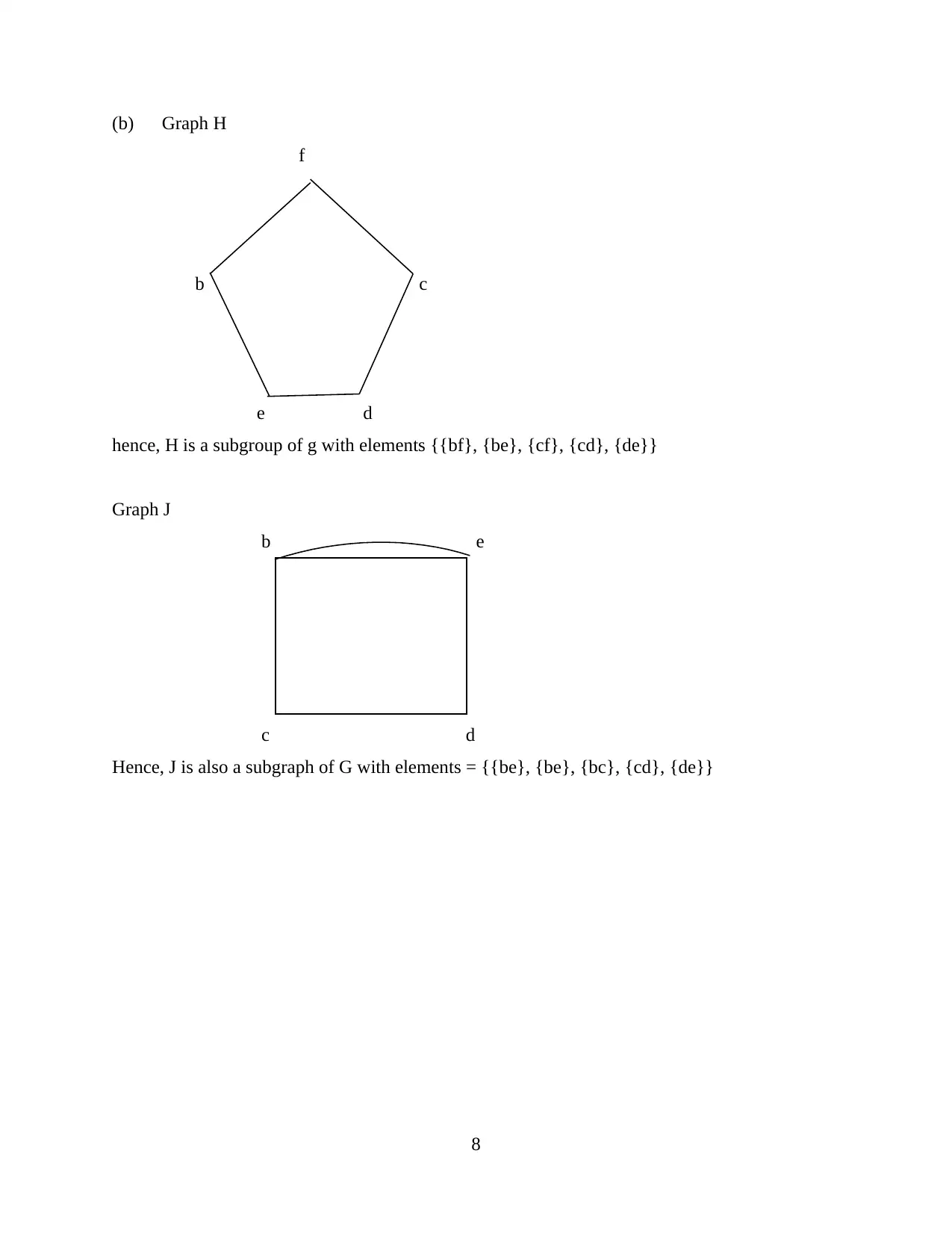
This document presents a comprehensive solution to a Mathematics for Computing assignment, covering several key areas within discrete mathematics. The solution begins with set theory, exploring the properties of sets and their relationships, including the image of a function and the concept of surjectivity. It then delves into combinatorics, calculating the number of possible program selections and arrangements, considering both ordered and unordered selections with and without repetition. Furthermore, the solution addresses graph theory, including adjacency matrices, graph representations, and the identification of subgraphs. The assignment also tackles the calculation of a minimal spanning tree and the determination of the shortest path in a weighted graph using algorithms like Dijkstra's algorithm, providing a detailed step-by-step approach to solving the problems.

Mathematics for Computing
1

Question 1
Solution
Given A = {1, 2, 3, 4} and B = {1, 2, 3}
(c)
A B
1
1
2
2
3
3
2

4
(a) Image of 3 is 1
(b) Co-domain of f = {1, 2, 3, 4}
(d) As each element of co-domain is mapped by one or two element of domain, therefore, the
given function is surjective.
3

Question 2
Solution:
Given – Number of programs = 10
(a) as only one program can be run at a time, where order doesn’t matter and with repetition of
elements, so, using k-selection
nCk = !n / k! (n-k)!
Taking k = 1
10C1 = !10 / 1! (10-1)!
= !10 / !9
= 10 ways
(b) Four programs are considered as higher in priority then –
nCk = !10 / !4 !6
= 210 ways
(c) Separating programs into three top priorities as –
3C1 + 5C1 + 2C1 ways
4

Question 3
(a) 1 2 3 4 5 6
1 F T T T F T
2 T F T F T F
3 T T F T T F
4 T F T F F F
5 F T T F F T
6 T F F F T F
2
1
3
6
4
5
5

Solution
A
B
C D E F
G
H
So, the weighted answer of minimal spanning tree = 52
6

Question 4
Solution
The present graph consists two finite sets as
vertex V = {a, b, c, d, e, f, g, h} and
edge E = {{ab}, {ac}, {ad}, {bc}, {be}, {be}, {bf}, {cd}, {ce}, {cf}, {de}, {gh}}
(a) Graph G =
b e
f
c d g h
a
7

(b) Graph H
f
b c
e d
hence, H is a subgroup of g with elements {{bf}, {be}, {cf}, {cd}, {de}}
Graph J
b e
c d
Hence, J is also a subgraph of G with elements = {{be}, {be}, {bc}, {cd}, {de}}
8

Question 5
Solution
Solution:
v A B C D E F G Z
A 0A 2A ∞ ∞ ∞ 1A ∞ ∞
F 2A 4F 1A 6F ∞
B 2A 4B 4B 6B ∞ ∞ ∞
C 4B 7C 5C
2 2 1
Shortest path – A B C Z = 5
S
9

10