Math for Computing: Differentiation and Integration Problems

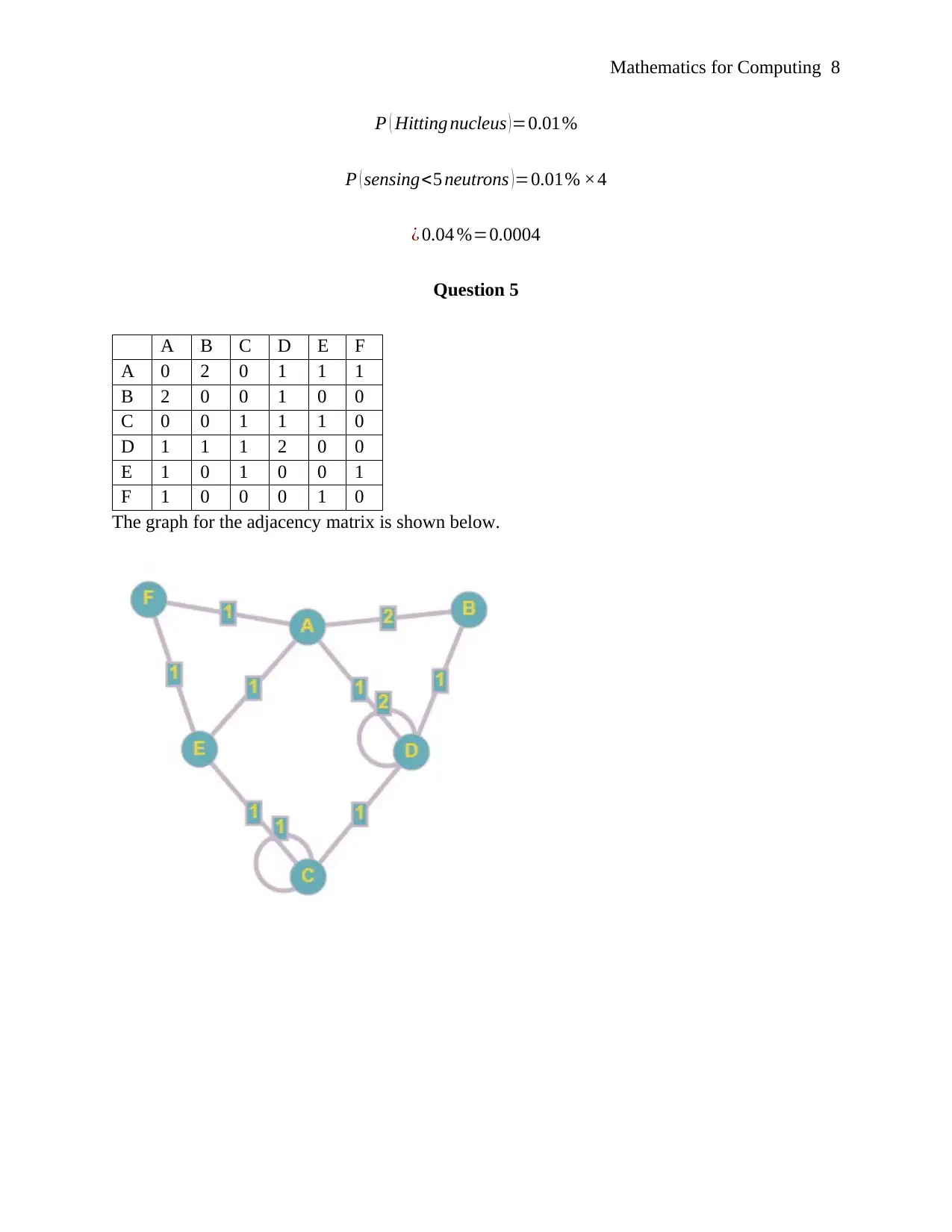
This document presents a comprehensive solution to a Mathematics for Computing assignment. It meticulously addresses several key mathematical concepts essential for computing. The solution begins with detailed calculations involving differentiation, including the application of the product and quotient rules to various functions. It then proceeds to integration, providing step-by-step solutions for both definite and indefinite integrals, including techniques such as substitution. Furthermore, the assignment explores graph theory, demonstrating the construction and interpretation of an adjacency matrix to represent a graph. Finally, the document includes a probability problem, calculating the likelihood of an event. The solutions are presented clearly, making this a valuable resource for students studying mathematics for computing.

Mathematics for Computing 1
Mathematics for Computing
Student’s Name
Course
Professor’s Name
University
City (State)
Date

Mathematics for Computing 2
Mathematics for Computing
Question 1
y= 2 x2 −1
x +2
dy
dx =lim
h → 0
y ( x +h ) − y ( x )
h =lim
h →0
2( x +h)2−1
x +h+2 − 2 x2−1
x +2
h
¿ lim
h→ 0
2 ( x2 +2 xh+h2 ) −1
x +h+2 − 2 x2−1
x +2
h =lim
h →0
2 x2 + 4 xh+2 h2−1
x+h+ 2 − 2 x2−1
x +2
h
¿ lim
h→ 0
( x+2 ) ( 2 x2+4 xh+2 h2−1 ) −(2 x2−1)(x+ h+2)
(x +h+2)( x +2)
h
¿ lim
h→ 0
4 x2 +8 xh+ 4 h2 +2 x3 + 4 x2 h+2 xh2−x−2−(2 x3 +2 x2 h+4 x2 −x−h−2)
( x+h+ 2)( x +2)
h
¿
lim
h → 0
4 x2 +8 xh+ 4 h2 +2 x3 + 4 x2 h+2 xh2−x−2−2 x3 −2 x2 h−4 x2+ x +h+ 2¿
( x +h+2)(x +2)
h ¿
¿
lim
h → 0
8 xh+4 h2+ 2 x2 h+h ¿
( x+h+2)(x +2)
h ¿=lim
h → 0
h (8 x+4 h+ 2 x2+ 1)
(x+ h+2)( x+2)
h =lim
h → 0
( 8 x + 4 h+2 x2+1)
( x+h+ 2)(x +2)
¿ (8 x +0+2 x2+1)
(x+ 0+2)(x+2) = 8 x +2 x2+1
( x +2 )2
dy
dx = 8 x +2 x2+1
( x +2 )2

Mathematics for Computing 3
Question 2(i)
y=3 x ( 4 x2 +5 x3 )5
dy
dx =3 d
dx (x) ( 4 x2+5 x3 ) 5
We apply the product rule ( f . g ) ' =f ' . g+ f . g'
f =x , f '= d
dx ( x )=1 , g= ( 4 x2+5 x3 )5
, g'= d
dx ( ( 4 x2+5 x3 ) ¿¿ 5)¿
In evaluating g' , let 4 x2 +5 x3=u∧f =u5
df (u)
dx = df
du . du
dx
df
du =5 u4
du
dx =4 ( 2 ) x1 +5 ( 3 ) x2=8 x +15 x2
df (u)
dx =g '=5 u4 ( 8 x+15 x2 )=5 ( 4 x2+5 x3 )4
( 8 x +15 x2 )
f ' . g+f . g' =1 ( 4 x2 +5 x3 )
5
+ 5 x ( 4 x2 +5 x3 ) 4
( 8 x+ 15 x2 )
¿ ( 4 x2+5 x3 )5
+5 x ( 4 x2+5 x3 )4
( 8 x +15 x2 )
dy
dx =3 ( ( 4 x2+5 x3 )5
+5 x ( 4 x2+ 5 x3 )4
( 8 x +15 x2 ) )
Question 2(ii)
y=sin (2 x ) cos(3 x2)

Mathematics for Computing 4
We apply the product rule ( f . g ) ' =f ' . g+ f . g'
f =sin ( 2 x ) , f '= d
dx ( sin ( 2 x ) ) =2cos ( 2 x )
g=cos ( 3 x2 ) , g'= d
dx cos ( 3 x2 )=−6 xsin ( 3 x2 )
( f . g ) ' =f ' . g+ f . g' =2 cos ( 2 x ) cos ( 3 x2 ) +(sin ( 2 x ) ¿) ( −6 xsin ( 3 x2 ) ) ¿
¿ 2 cos ( 2 x ) cos (3 x2 )−6 xsin ( 3 x2 ) ¿ ¿
Question 2(iii)
y=4 x2 log5 (3 x)
but log5 (3 x)= ln 3 x
ln5
y=4 x2 log5 (3 x)=4 x2 ln 3 x
ln 5 = 4
ln 5 x
2
ln(3 x)
dy
dx = 4
ln 5
d
dx x2 ln (3 x )
In evaluating d
dx x2 ln(3 x ),we apply the product rule ( f . g )' =f ' . g+ f . g'
f =x2 , f '=2 x
g=ln ( 3 x ) , g' = 1
x
f ' . g+f . g' =2 x ln ( 3 x ) + x2 . 1
x =2 xln ( 3 x )+ x

Mathematics for Computing 5
dy
dx = 4
ln5
d
dx x2 ln(3 x )= 4
ln 5 ( 2 xln ( 3 x ) + x )
dy
dx = 4
ln 5 ( 2 xln ( 3 x )+ x )
Question 2(iv)
y= 2 x3
tan(2 x )
dy
dx =2 d
dx
x3
tan (2 x )
Using the quotient rule , d
dx
x3
tan(2 x)=tan(2 x ) d
dx
( x ¿¿ 3)−x3 d
dx tan ( 2 x )
tan2 (2 x) ¿
¿ 3 x2 tan(2 x) x2−2 x3 sec2 ( 2 x )
tan2 (2 x)
Question 3(i)
∫2 ( x2 +4 x−1 +2 x−2 ) dx=2∫ ( x2 + 4 x−1+ 2 x−2 ) dx
¿ 2∫ x2 dx +2(4 )∫ 1
x dx +2(2)∫ x−2 dx
¿ 2 x2+1
2+1 +8 ln ( x )+ 4 x−2+1
−2+1 +C
¿ 2
3 x3+ 8 ln ( x )−4 x−1+C
Question 3(ii)
∫ x2 cos ( 2 x ) dx

Mathematics for Computing 6
∫udv=uv−∫ vdu
Let x2=u , du=2 xdx∧dv=cos (2 x) so that:
v=∫ dv=¿ 1
2 sin (2 x )¿
uv−∫ vdu=x2 . 1
2 sin ( 2 x )−∫ 1
2 sin ( 2 x ) 2 xdx= 1
2 x2 sin ( 2 x )−∫ x sin ( 2 x ) dx
In evaluating ∫ x sin ( 2 x ) dx:
Let x=u , du=dx∧dv =sin (2 x) so that:
v=∫ dv=−¿ 1
2 cos (2 x)¿
uv−∫ vdu=x (−1
2 cos ( 2 x ) )−∫ −1
2 cos ( 2 x ) dx =−1
2 xcos ( 2 x ) + 1
2 ( 1
2 )sin ( 2 x )
∫ x sin ( 2 x ) dx=−1
2 xcos ( 2 x )+ 1
4 sin ( 2 x )
∫ x2 cos ( 2 x ) dx= 1
2 x2 sin ( 2 x )−(−1
2 xcos ( 2 x ) + 1
4 sin ( 2 x ) )
¿ 1
2 x2 sin ( 2 x ) + 1
2 xcos (2 x )− 1
4 sin ( 2 x )
Question 3(iii)
∫cos ( 2 x ) dx
let 2 x=u ,du=2 dx ,dx =1
2 du

Mathematics for Computing 7
∫cos ( 2 x ) dx=∫cos ( u ) . 1
2 du
¿ 1
2∫ cos ( u ) du=1
2 sin (u ) +C=1
2 sin ( 2 x ) +C
Question 3(iv)
∫
x=2
x=5
6 x3+ 7 x2 +6 x +2
x +2 dx
6 x3 +7 x2 +6 x+ 2
x +2 =3 x2 + 4 x2 +6 x+21
2 x +1
¿ 3 x2+2 x + 4 x +2
2 x +1
¿ 3 x2+2 x +2
∫
x=2
x=5
6 x3+ 7 x2 +6 x +2
x +2 dx= ∫
x=2
x=5
(3 x2 +2 x +2¿) dx ¿
∫(3 x2 +2 x+ 2)dx= 3 x2 +1
2+1 + 2 x1+1
1+1 +2 x =x3 + x2 +2 x
∫
x=2
x=5
(3 x2+2 x +2¿)dx=x3 + x2 +2 x ¿x=2
x=5 ¿
¿ ( (5)3+(5)2+ 2(5))−(2¿¿ 3+22 +2(2))¿
¿ ( 125+25+10 )− ( 8+ 4+4 ) =160−16
¿ 144
Question 4

Mathematics for Computing 8
P ( Hitting nucleus ) =0.01%
P ( sensing<5 neutrons )=0.01% ×4
¿ 0.04 %=0.0004
Question 5
A B C D E F
A 0 2 0 1 1 1
B 2 0 0 1 0 0
C 0 0 1 1 1 0
D 1 1 1 2 0 0
E 1 0 1 0 0 1
F 1 0 0 0 1 0
The graph for the adjacency matrix is shown below.

Mathematics for Computing 9