HNCB 8 Mathematics for Construction: Problem Solutions and Analysis
VerifiedAdded on 2023/05/30
|31
|6163
|245
Homework Assignment
AI Summary
This document presents a comprehensive set of solutions for a HNCB 8 Mathematics for Construction assignment. It covers a wide range of mathematical concepts relevant to construction, including calculations for tank dimensions, speed and fuel consumption, and lift proportionalities. The solutions delve into sequences, geometric progressions, and logarithmic and hyperbolic functions, providing step-by-step approaches. Additionally, the document includes statistical analysis of revenue data, involving frequency distributions and quartile calculations. It addresses problems in calculus, such as solving equations and applying concepts to construction-related scenarios. The assignment covers various tasks with multiple scenarios, ensuring a thorough understanding of mathematical methods applicable to construction projects.

Problem Solution
1 | P a g e
HNCB 8 MATHEMATIC FOR
CONSTRUCTION
1 | P a g e
HNCB 8 MATHEMATIC FOR
CONSTRUCTION
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Problem Solution
Contents
TASK 1 SCENARIO 1....................................................................................................................4
Solution 1.....................................................................................................................................4
Solution 2.....................................................................................................................................4
TASK 1 SCENARIO 2....................................................................................................................5
Solution a)....................................................................................................................................5
Solution b)...................................................................................................................................5
TASK 1 SCENARIO 3....................................................................................................................6
Solution 1.....................................................................................................................................6
Solution 2.....................................................................................................................................7
Solution 3a...................................................................................................................................7
Solution 3b...................................................................................................................................8
Solution 3c...................................................................................................................................8
TASK 2 SCENARIO 1..................................................................................................................11
TASK 2 SCENARIO 2..................................................................................................................17
Solution A..................................................................................................................................17
Solution B..................................................................................................................................19
TASK 3 SCENARIO 1..................................................................................................................19
TASK 3 SCENARIO 2..................................................................................................................24
TASK 4 SCENARIO 1..................................................................................................................26
Solution a.i)................................................................................................................................26
Solution a.ii)..............................................................................................................................26
Solution b).................................................................................................................................26
Solution c)..................................................................................................................................27
TASK 4 SCENARIO 2..................................................................................................................27
Solution a)..................................................................................................................................27
Solution b).................................................................................................................................28
Solution c)..................................................................................................................................28
Solution d).................................................................................................................................28
TASK 4 SCENARIO 3..................................................................................................................29
2 | P a g e
Contents
TASK 1 SCENARIO 1....................................................................................................................4
Solution 1.....................................................................................................................................4
Solution 2.....................................................................................................................................4
TASK 1 SCENARIO 2....................................................................................................................5
Solution a)....................................................................................................................................5
Solution b)...................................................................................................................................5
TASK 1 SCENARIO 3....................................................................................................................6
Solution 1.....................................................................................................................................6
Solution 2.....................................................................................................................................7
Solution 3a...................................................................................................................................7
Solution 3b...................................................................................................................................8
Solution 3c...................................................................................................................................8
TASK 2 SCENARIO 1..................................................................................................................11
TASK 2 SCENARIO 2..................................................................................................................17
Solution A..................................................................................................................................17
Solution B..................................................................................................................................19
TASK 3 SCENARIO 1..................................................................................................................19
TASK 3 SCENARIO 2..................................................................................................................24
TASK 4 SCENARIO 1..................................................................................................................26
Solution a.i)................................................................................................................................26
Solution a.ii)..............................................................................................................................26
Solution b).................................................................................................................................26
Solution c)..................................................................................................................................27
TASK 4 SCENARIO 2..................................................................................................................27
Solution a)..................................................................................................................................27
Solution b).................................................................................................................................28
Solution c)..................................................................................................................................28
Solution d).................................................................................................................................28
TASK 4 SCENARIO 3..................................................................................................................29
2 | P a g e

Problem Solution
TASK 1 SCENARIO 1
Solution 1
As given in problem,
Since there is no description of height of the tank, in this condition, Area given must be area of
the bottom of the tank.
Suppose the width is b, The length l will = b + 3.2 m
Area of the bottom od the surface = b(b+3.2) = 26.5 m2
b2+3.2 b−26.5=0
The root of the equation will be given rectangular tank,
The roots of the equation will be
x1,2=−b ± √b2−4 ac
2 a =3.2 ± √3.22 −4 x 26.5
2 =3.2 ± √10.24 +106
2
x1,2=−3.2 ± √10.24+106
2 =−3.2 ± 10.78
2
x1,2=−1.6−5.39 ,∧−1.6+ 5.39
x1,2=−6.990733 ,∧3.7907
Since negative length is not accepted, the width is = b = 3.7907
Then length will be l = 3.7907+3.2 = 6.990733 m Ans
Solution 2
Suppose daily forfeited amount = £ x,
And Contract amount =£ y
For 5 days late, the contractor receives, y – 5x = £ 4250…………. (i)
For 12 days late the contractor receives, y-12x =£ 2120………. (ii)
Subtracting the equation (ii) from equation (i)
3 | P a g e
TASK 1 SCENARIO 1
Solution 1
As given in problem,
Since there is no description of height of the tank, in this condition, Area given must be area of
the bottom of the tank.
Suppose the width is b, The length l will = b + 3.2 m
Area of the bottom od the surface = b(b+3.2) = 26.5 m2
b2+3.2 b−26.5=0
The root of the equation will be given rectangular tank,
The roots of the equation will be
x1,2=−b ± √b2−4 ac
2 a =3.2 ± √3.22 −4 x 26.5
2 =3.2 ± √10.24 +106
2
x1,2=−3.2 ± √10.24+106
2 =−3.2 ± 10.78
2
x1,2=−1.6−5.39 ,∧−1.6+ 5.39
x1,2=−6.990733 ,∧3.7907
Since negative length is not accepted, the width is = b = 3.7907
Then length will be l = 3.7907+3.2 = 6.990733 m Ans
Solution 2
Suppose daily forfeited amount = £ x,
And Contract amount =£ y
For 5 days late, the contractor receives, y – 5x = £ 4250…………. (i)
For 12 days late the contractor receives, y-12x =£ 2120………. (ii)
Subtracting the equation (ii) from equation (i)
3 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Problem Solution
y- 5x -y+12x = 4250-2120, 7x = 2130, or x = £ 304.29,
The late penalty amount = £ 304.29
The original contract amount = y = 2120 + 7x304.29 =£ 2130.3 +£ 2120 = £ 4250.03
TASK 1 SCENARIO 2
Solution a)
The speed of the car is 65 miles /hr
Speed in meter / second
65 miles/hr = 65*1760/3600 = 31.77 yards /sec,
The speed in meter /sec = 31.77 * 0.91 = 28.917 m/sec
The time taken to drive 100 mile = 100/65 = 1.54 hrs Ans
Fuel consumption, 30 mile /gallon
= 30*1760 yards / gallon = 30*1760*0.91 / 3.78 litres
= 48048 / 3.78 = 12711 / litres = 12.711 km /litres
The amount in litres per kilometre = 0.0786 litres / km Ans
The completed journey of 100 mile = 100*1760*0.91/1000 = 160.16 km
Since, the consumption of fuel = 0.0786 litres / km
Then, fuel required for complete journey = 0.0786 x 160.16 = 12.59 litres
Solution b)
As given in question, lift is directly proportional to air density, air speed, and surface area,
All in MKS unit
Units of area = m2
Unit of density = kg/m3
Unit of velocity = m/s
Then, Lift =k x ρx V 2 x A
4 | P a g e
y- 5x -y+12x = 4250-2120, 7x = 2130, or x = £ 304.29,
The late penalty amount = £ 304.29
The original contract amount = y = 2120 + 7x304.29 =£ 2130.3 +£ 2120 = £ 4250.03
TASK 1 SCENARIO 2
Solution a)
The speed of the car is 65 miles /hr
Speed in meter / second
65 miles/hr = 65*1760/3600 = 31.77 yards /sec,
The speed in meter /sec = 31.77 * 0.91 = 28.917 m/sec
The time taken to drive 100 mile = 100/65 = 1.54 hrs Ans
Fuel consumption, 30 mile /gallon
= 30*1760 yards / gallon = 30*1760*0.91 / 3.78 litres
= 48048 / 3.78 = 12711 / litres = 12.711 km /litres
The amount in litres per kilometre = 0.0786 litres / km Ans
The completed journey of 100 mile = 100*1760*0.91/1000 = 160.16 km
Since, the consumption of fuel = 0.0786 litres / km
Then, fuel required for complete journey = 0.0786 x 160.16 = 12.59 litres
Solution b)
As given in question, lift is directly proportional to air density, air speed, and surface area,
All in MKS unit
Units of area = m2
Unit of density = kg/m3
Unit of velocity = m/s
Then, Lift =k x ρx V 2 x A
4 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Problem Solution
Lift =k x kg
m3 x m
s x m2=kg/sec
The unit for lift = kg/sec Ans
TASK 1 SCENARIO 3
Solution 1
1 the Athematic sequence as given b, 2b/3, b/3, 0
The difference in the term = 2b
3 −b=2 b−3 b
3 =−b
3
The common difference = −b
3
The first term = b,
The 6th term will be = a1 + (6-1) d Putting the values,
= b− 6 b
3 − b
3 = 3 b−6 b−b
3 =−4 b
3 Ans
The kth term will be = a1 + (k-1) d Putting the values,
= b− kb
3 − b
3 = 3 b−kb−b
3 = 2 b−kb
3 Ans
The 20th term will be = 2b−kb
3 =2 b−20∗b
3 =−18 b
3
As given in question, −18 b
3 =15 ,
-18b = 45, b = -45/18 = -5/2
The value of b = -5/2 Ans
The sum of first 20th term,
5 | P a g e
Lift =k x kg
m3 x m
s x m2=kg/sec
The unit for lift = kg/sec Ans
TASK 1 SCENARIO 3
Solution 1
1 the Athematic sequence as given b, 2b/3, b/3, 0
The difference in the term = 2b
3 −b=2 b−3 b
3 =−b
3
The common difference = −b
3
The first term = b,
The 6th term will be = a1 + (6-1) d Putting the values,
= b− 6 b
3 − b
3 = 3 b−6 b−b
3 =−4 b
3 Ans
The kth term will be = a1 + (k-1) d Putting the values,
= b− kb
3 − b
3 = 3 b−kb−b
3 = 2 b−kb
3 Ans
The 20th term will be = 2b−kb
3 =2 b−20∗b
3 =−18 b
3
As given in question, −18 b
3 =15 ,
-18b = 45, b = -45/18 = -5/2
The value of b = -5/2 Ans
The sum of first 20th term,
5 | P a g e

Problem Solution
S20th=2 a1+ ( n−1 ) d
2 . n
S20th=2 b− ( 20−1 ) b /3
2 .20= 6 b−19 b
6 x 20=−13 b
3 x 10
Putting the value of b,
= −13
3 x− 5
2 x 10= 20∗13
3 =260/3 Ans
Solution 2
First, we must fine common ration of the given =
1
2
1 =1
2
The nth term is given as = arn-1
The 20th term = 1. ( 1
2 )20−1
= 1
219 =1.90735 x 10-06 Ans
The sum of the geometric progression = Sn= a (1−r n)
1−r
If the series goes to infinity,
S∝= a(1−r∝)
1−r ……(i)
As we can see that, the common ratio of the given GP is ½, in this condition, value rn will
become smaller and smaller and if n = infinite, then rn will be equal to zero.
In this condition, the equation (i) will become
S∝= a(1−r∝)
1−r = a
1−r Ans
Solution 3a
2log(3x) + log(18x) = 27
2log(3x) + log (32 Xx 2) = 27
2log(3x) +2log(3x) +log (2) = 27
4log(3x) = 27-0.301 = 26.699, or log(3x) = 26.699/4 = 6.67475
6 | P a g e
S20th=2 a1+ ( n−1 ) d
2 . n
S20th=2 b− ( 20−1 ) b /3
2 .20= 6 b−19 b
6 x 20=−13 b
3 x 10
Putting the value of b,
= −13
3 x− 5
2 x 10= 20∗13
3 =260/3 Ans
Solution 2
First, we must fine common ration of the given =
1
2
1 =1
2
The nth term is given as = arn-1
The 20th term = 1. ( 1
2 )20−1
= 1
219 =1.90735 x 10-06 Ans
The sum of the geometric progression = Sn= a (1−r n)
1−r
If the series goes to infinity,
S∝= a(1−r∝)
1−r ……(i)
As we can see that, the common ratio of the given GP is ½, in this condition, value rn will
become smaller and smaller and if n = infinite, then rn will be equal to zero.
In this condition, the equation (i) will become
S∝= a(1−r∝)
1−r = a
1−r Ans
Solution 3a
2log(3x) + log(18x) = 27
2log(3x) + log (32 Xx 2) = 27
2log(3x) +2log(3x) +log (2) = 27
4log(3x) = 27-0.301 = 26.699, or log(3x) = 26.699/4 = 6.67475
6 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Problem Solution
Log(3x) = 6.67475
Removing log from above
3x = 106.67475 = 550321470
X = 183440490 Ans
Solution 3b
2Log.e(3x) + Loge(18x) = 9
This is the function of natural logarithm, first we will resolve the equation as above, then
wo will solve it.
2loge (3x) + loge (18x) = 9
2loge (3x) + loge (32X x 2)
2loge (3x) + 2loge (3x) +loge (2)
4loge (3x) + loge (2) = 9
4loge (3x) = 9-0.693
4loge (3x) = 8.306853
loge (3x) = 2.077
3x = e2.077 = 11.056
X = 3.685316 Ans
Solution 3c
i) Cosh(X) + Sinh(X) = 5
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
Putting the value in question
1
2 ( ex +e− x ) + 1
2 ( ex−e− x ) =5
7 | P a g e
Log(3x) = 6.67475
Removing log from above
3x = 106.67475 = 550321470
X = 183440490 Ans
Solution 3b
2Log.e(3x) + Loge(18x) = 9
This is the function of natural logarithm, first we will resolve the equation as above, then
wo will solve it.
2loge (3x) + loge (18x) = 9
2loge (3x) + loge (32X x 2)
2loge (3x) + 2loge (3x) +loge (2)
4loge (3x) + loge (2) = 9
4loge (3x) = 9-0.693
4loge (3x) = 8.306853
loge (3x) = 2.077
3x = e2.077 = 11.056
X = 3.685316 Ans
Solution 3c
i) Cosh(X) + Sinh(X) = 5
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
Putting the value in question
1
2 ( ex +e− x ) + 1
2 ( ex−e− x ) =5
7 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Problem Solution
⟹ ( ex +e− x ) + ( ex−e− x )=10
⟹ ( ex ) + ( ex ) =10
⟹ 2 ex=10
⟹ ex=5 Taking natural log on both side
X = loge (5) = 1.609 Ans
(ii) Cosh(2Y) – Sin.h(2Y) = 3
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( 2Y ) =1
2 (e2 Y +e−2Y )
Similarly, sinh ( 2 Y ) = 1
2 (e2 Y −e−2 Y )
cosh ( 2Y ) – sinh ( 2 Y ) =3
⇒ 1
2 ( e2 Y + e−2Y ) −1
2 ( e2 Y −e−2 Y )=3
⇒ ( e2 Y + e−2 Y ) − ( e2 Y −e−2Y ) =6
⇒ e−2 Y +e−2 Y =6
⇒ e−2 Y =3 Putting natural log on both side
⇒ Lo ge e−2Y =loge 3 Same base is cancelled
-2Y = 1.098612
Y = -1.098612/2 = -0.55 Ans
(iii) Cosh(K) * Sinh(K) = 2
8 | P a g e
⟹ ( ex +e− x ) + ( ex−e− x )=10
⟹ ( ex ) + ( ex ) =10
⟹ 2 ex=10
⟹ ex=5 Taking natural log on both side
X = loge (5) = 1.609 Ans
(ii) Cosh(2Y) – Sin.h(2Y) = 3
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( 2Y ) =1
2 (e2 Y +e−2Y )
Similarly, sinh ( 2 Y ) = 1
2 (e2 Y −e−2 Y )
cosh ( 2Y ) – sinh ( 2 Y ) =3
⇒ 1
2 ( e2 Y + e−2Y ) −1
2 ( e2 Y −e−2 Y )=3
⇒ ( e2 Y + e−2 Y ) − ( e2 Y −e−2Y ) =6
⇒ e−2 Y +e−2 Y =6
⇒ e−2 Y =3 Putting natural log on both side
⇒ Lo ge e−2Y =loge 3 Same base is cancelled
-2Y = 1.098612
Y = -1.098612/2 = -0.55 Ans
(iii) Cosh(K) * Sinh(K) = 2
8 | P a g e

Problem Solution
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( K )= 1
2 (eK + e−K )
Similarly, sinh ( K )= 1
2 (eK −e− K )
⇒ 1
2 ( e K +e− K ) x 1
2 ( eK −e− K ) =2
⇒ ( eK +e− K ) x ( eK−e−K ) =8
⇒ ( e2 K−e−2 K ) =8
e2 K = √ 4 + √17 and e2 K =− √ 4 + √ 17 Taking log on both side
For e2 K =− √4 + √ 17 No solution for K ∈ R
Then, e2 K = √ 4 + √ 17
And K= 1
2 ln ( 4+ √17 )=1.04736 Ans
(iv) Cosh(M) / Sinh(M) = 2
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( M )=1
2 ( eM+ e−M )
Similarly, sinh ( M )= 1
2 ( eM−e−M )
9 | P a g e
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( K )= 1
2 (eK + e−K )
Similarly, sinh ( K )= 1
2 (eK −e− K )
⇒ 1
2 ( e K +e− K ) x 1
2 ( eK −e− K ) =2
⇒ ( eK +e− K ) x ( eK−e−K ) =8
⇒ ( e2 K−e−2 K ) =8
e2 K = √ 4 + √17 and e2 K =− √ 4 + √ 17 Taking log on both side
For e2 K =− √4 + √ 17 No solution for K ∈ R
Then, e2 K = √ 4 + √ 17
And K= 1
2 ln ( 4+ √17 )=1.04736 Ans
(iv) Cosh(M) / Sinh(M) = 2
Since the value of cosh ( x )= 1
2 ( ex+ e−x)
And sinh(x )= 1
2 (ex−e− x)
The value of cosh ( M )=1
2 ( eM+ e−M )
Similarly, sinh ( M )= 1
2 ( eM−e−M )
9 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Problem Solution
1
2 ( eM +e− M )
1
2 ( eM−e−M )
=2
⇒ ( e M + e−M )
( eM −e−M ) =2 Multiplying both side by ( e M−e− M )
⇒ ( eM +e−M ) ( eM−e−M )
( eM−e− M ) =2 ( e M−e−M )
Solving the above equation
eM = √ 3 ,e M =− √ 3 ,
Solving, eM = √ 3 M = 1
2 ln ( 3 ) =0.54931
eM =− √ 3 No solution K ∈ R
Then M = 0.54931 Ans
TASK 2 SCENARIO 1
a)
10 | P a g e
1
2 ( eM +e− M )
1
2 ( eM−e−M )
=2
⇒ ( e M + e−M )
( eM −e−M ) =2 Multiplying both side by ( e M−e− M )
⇒ ( eM +e−M ) ( eM−e−M )
( eM−e− M ) =2 ( e M−e−M )
Solving the above equation
eM = √ 3 ,e M =− √ 3 ,
Solving, eM = √ 3 M = 1
2 ln ( 3 ) =0.54931
eM =− √ 3 No solution K ∈ R
Then M = 0.54931 Ans
TASK 2 SCENARIO 1
a)
10 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Problem Solution
0-5 5 - 10 10-15 15-20 20-30 30-40
0
1
2
3
4
5
6
7
8
9
Histogram for January data
Revenue
Frequency Density
0-5 5 - 10 10-15 15-20 20-30 30-40
0
2
4
6
8
10
12
14
16
Histogram for July data
Revenue
Frequency Density
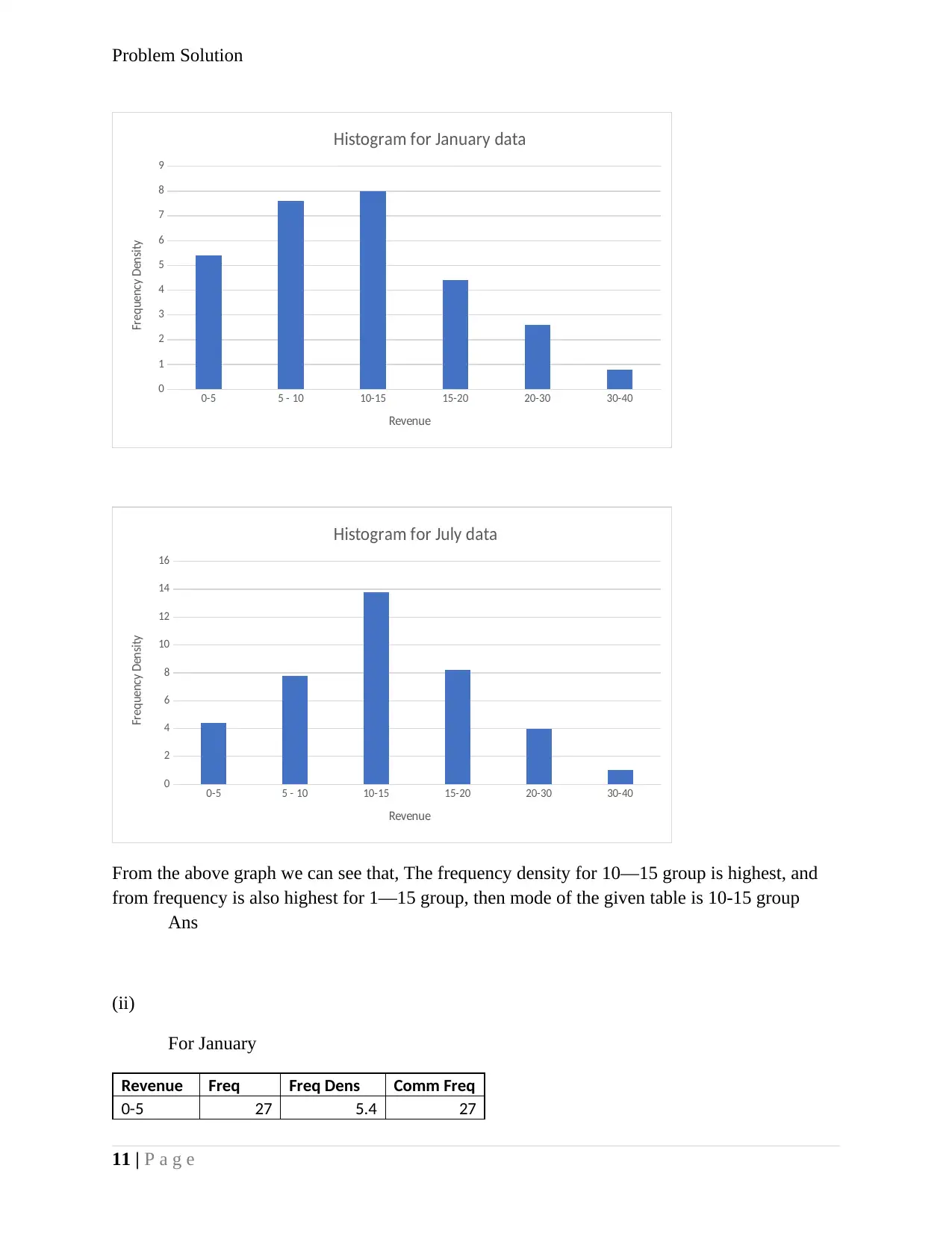
From the above graph we can see that, The frequency density for 10—15 group is highest, and
from frequency is also highest for 1—15 group, then mode of the given table is 10-15 group
Ans
(ii)
For January
Revenue Freq Freq Dens Comm Freq
0-5 27 5.4 27
11 | P a g e
0-5 5 - 10 10-15 15-20 20-30 30-40
0
1
2
3
4
5
6
7
8
9
Histogram for January data
Revenue
Frequency Density
0-5 5 - 10 10-15 15-20 20-30 30-40
0
2
4
6
8
10
12
14
16
Histogram for July data
Revenue
Frequency Density
From the above graph we can see that, The frequency density for 10—15 group is highest, and
from frequency is also highest for 1—15 group, then mode of the given table is 10-15 group
Ans
(ii)
For January
Revenue Freq Freq Dens Comm Freq
0-5 27 5.4 27
11 | P a g e

Problem Solution
5 - 10 38 7.6 65
10-15 40 8 105
15-20 22 4.4 127
20-30 13 2.6 140
30-40 4 0.8 144
For July
Revenue July
Freq
Dens
Comm
Freq
0-5 22 4.4 22
5 - 10 39 7.8 61
10-15 69 13.8 130
15-20 41 8.2 171
20-30 20 4 191
30-40 5 1 196
For January table,
Since N = 144 Observation,
The position of first quartile
Q1=|144+ 1
4 |=|145
4 |=|36th+ 1
4 (36th¿35th)|
As per above calculation,
From cumulative frequency 36th value is 14th value in class 5-10,
J = 14, f = 39, L = 5, U = 10
The observation of 12th estimation
L+( j− 1
2 ) x (U −L)
f =5+ (14−0.5 ) ( 10−5 )
39 =6.731
Since 37th value and 15th value are in same class.
¿ 5+ ( 15− 1
2 ) x (10−5)
39 =5+ ( 17−0.5 ) ( 10−5 )
39 =6.85
12 | P a g e
5 - 10 38 7.6 65
10-15 40 8 105
15-20 22 4.4 127
20-30 13 2.6 140
30-40 4 0.8 144
For July
Revenue July
Freq
Dens
Comm
Freq
0-5 22 4.4 22
5 - 10 39 7.8 61
10-15 69 13.8 130
15-20 41 8.2 171
20-30 20 4 191
30-40 5 1 196
For January table,
Since N = 144 Observation,
The position of first quartile
Q1=|144+ 1
4 |=|145
4 |=|36th+ 1
4 (36th¿35th)|
As per above calculation,
From cumulative frequency 36th value is 14th value in class 5-10,
J = 14, f = 39, L = 5, U = 10
The observation of 12th estimation
L+( j− 1
2 ) x (U −L)
f =5+ (14−0.5 ) ( 10−5 )
39 =6.731
Since 37th value and 15th value are in same class.
¿ 5+ ( 15− 1
2 ) x (10−5)
39 =5+ ( 17−0.5 ) ( 10−5 )
39 =6.85
12 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 31
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




