Mathematics Assignment: Analyzing Equations, Integrals, and Matrices

This mathematics assignment solution covers a range of topics, including linear algebra, calculus, and problem-solving. The first question involves analyzing population dynamics using matrix equations, calculating eigenvalues and eigenvectors, and applying these concepts to predict population sizes over time. The second question focuses on curve analysis, finding equations for highways and railways, and calculating areas using integration. The third question explores quadratic equations, reservoir volume calculations, and the application of differentiation. The final question involves setting up and solving systems of linear equations using Gaussian elimination to determine Tim Tam consumption patterns. The assignment demonstrates a comprehensive understanding of mathematical concepts and their applications.

Running head: MATHEMATICS
MATHEMATICS
Name of the Student
Name of the University
Author Note

1MATHEMATICS
Question 1:
The population of rabbits and foxes are related by the following equations.
rn +1= 4 r n−2 f n
3
f n+1= rn + f n
3
a) The equations can be represented by a matrix form
[ rn +1
f n +1 ]=
[ 4
3
−2
3
1
3
1
3 ] [ rn
f n ]
Here, M =
[ 4
3
−2
3
1
3
1
3 ]
b) The inverse of the matrix M is calculated by the following formula.
M−1 = Adj(M)/Det(M)
Where, Adj(M) =
[ 1
3
−1
3
2
3
4
3 ]T
=
[ 1
3
2
3
−1
3
4
3 ]
Det(M) = (4/3)*(1/3) + (2/3)*(1/3) = 4/9 + 2/9 = 6/9 = 2/3.
Hence, M−1 = [ 1
3
2
3
−1
3
4
3 ](2/3)
=
[ 1
2 1
−1
2 2 ]
c) The eigenvalues of M are calculated from the following equation.

2MATHEMATICS
det(M – λI) = 0
Here, I is the identity matrix.
Hence, det(
[ 4
3
−2
3
1
3
1
3 ]− [ λ 0
0 λ ]) = 0
Now, the eigenvalues found from the above equation are λ 1 = 1 and λ 2 = 2/3.
d) Now, the eigenvectors for each of the eigenvalues are calculated by constructing the
augmented matrix for each Eigen value and then converting it to row echelon form and then
obtaining the eigenvectors from system of linear equation.
The augmented matrix is given by,
(M – λ 1∗I : 0) =
[ 4
3 −1 −2
3 0
1
3
1
3 −1 0 ] =
[ 1
3
−2
3 0
1
3
−2
3 0 ]
Now, converting to row echelon form
[ 1
3
−2
3 0
1
3
−2
3 0 ] = [ 1
3
−2
3 0
0 0 0 ] (R2 = R2 – R1)
Hence, x1*(1/3) – x2*(2/3) = 0 => x1 = 2*x2
Hence, the eigenvector x = [ 2 x 2
x 2 ] = [ 2
1 ] x 2
For any real x2 ≠ 0, [2
1 ] x 2 are the eigenvectors associated with the eigenvalue λ 1 = 1.
Now, similarly for λ 2 = 2/3

3MATHEMATICS
(M – λ 1∗I : 0) =
[ 4
3 − 2
3
−2
3 0
1
3
1
3 − 2
3 0 ] =
[ 2
3
−2
3 0
1
3
−1
3 0 ] = [ 2
3
−2
3 0
0 0 0 ](R2 [= R2 – (½)R1)
Hence, in this case eigenvector y = [ y 2
y 2 ] = [ 1
1 ]y2
For any real y2 ≠ 0, [1
1 ] y 2 are the eigenvectors associated with the eigenvalue λ 2 = 2/3.
e) Now, for diagonalization of matrix M the linearly independent eigenvectors are found.
From the above it can be seen that x = [ 2
1 ] and [ 1
1 ] are linearly independent.
Hence, the invertible matrix P = [x ; y] = [2 1
1 1 ]
Now, the diagonal matrix has the eigenvalues in the diagonal position.
Hence, D = [ 1 0
0 2
3 ]
Hence, the matrix M can be diagonalized by,
P∗D∗P−1 = M
It can be seen that by matrix multiplication and calculating P−1 gives
[ 4
3
−2
3
1
3
1
3 ]which is the
matrix M.
f) Now, the determinant of M = product of eigenvalues = (2/3)*1 = 2/3.
Also, the eigenvalues of diagonal matrix D is the diagonal elements.

4MATHEMATICS
Hence, determinant of D = 2/3.
Hence, as n goes large the values of Dn and M n will approach 0 as 2/3 is less than unity.
g) Now, the current year is 2019. Hence, the difference from 1819 is 200 years.
Now, [ r200
f 200 ]=
[ 4
3
−2
3
1
3
1
3 ] [ r199
f 199 ]
Or, [r200
f 200 ]=
[ 4
3
−2
3
1
3
1
3 ]200
[r0
f 0 ]
Now,
[ 4
3
−2
3
1
3
1
3 ]200
= P*(D^200)*P^(-1)
P^(-1) = [ 1 −1
−1 2 ], P = [2 1
1 1 ]
Now, D^200 = [1 0
0 ( 2
3 )200
] = [ 1 0
0 0 ] (as 200 is a large number (2/3)^200 ~ 0)
Hence, P*(D^200)*P^(-1) = [ 2 1
1 1 ]∗[ 1 0
0 0 ]∗[ 1 −1
−1 2 ] = [2 −2
1 −1 ]
Hence, [r200
f 200 ]= [2 −2
1 −1 ] [r0
f 0 ]
=> [r200
f 200 ]=¿ [ 2 −2
1 −1 ][ 1800
40 ]
Hence, r200 = 2*1800 – 2*40 = 3600 – 80 = 3520 rabbits.

5MATHEMATICS
f 200 = 1800 – 40 = 1760 foxes.
Question 2:
The course model of the river is given by
r(x) = -x^4 + 12x^3 -54x^2 + 110x – 85
a) The highway intersects r(x) at x = 3/2 and x = 9/2.
Hence, r(3/2) = -6.0625 and r(9/2) = -0.0625
Hence, as the highway is straight the equation of highway will be
(h – (-6.0625))/(x - 3/2) = (-6.0625 – (-0.0625))/(3/2 – 9/2)
(h + 6.0625)/(x-1.5) = 2
 (h + 6.0625) = 2x – 3 => h = 2x – 9.0625
b) The straight railway meets the river in two points x = 3 and x = (½)(3^(4/3) + 6) = 5.1634
Hence, r(3) = 2 and r(5.1634) = -15.5784.
Hence, equation of railway
(R – 2)/(x - 3) = (2 + 15.5784)/(3 – 5.1634)
 R-2 = (x-3)* -8.1254 => R = -8.1254x +24.3762 + 2
 R(x) = -8.1254x +26.3762
c) Now, the points in L1 are modelled by equation
f(x) = -x^4 + 12*x^3 -54*x^2 + 110x – 85 when 3<=x <= 5.1634
The points in L2 are bounded by (3,2), (5.1634, -15.5784),(3,0),(5.1634,0).
d) The area L1 can be found by following integration formula

6MATHEMATICS
area L1 = ∫
3
5.1634
(−x4 +12∗x3−54∗x2 +110 x – 85)− ( −8.1254 x+24.3762+ 2 ) dx = 14.217
unit^2.
The area L2 = ∫
3
5.1634
( −8.1254 x +26.3762 ) dx= 14.68 unit^2.
Hence, the area L2 is larger than area L1.
Question 3:
a) Given curve equation is
f(x) = ax^2 + bx + c
The points on the curve are (0,0), (50,-25) and (100,0)
So, f(0) = c => c = 0
f(50) = 50^2*a + 50b => 2500a + 50b => 2500a + 50b = -25 (i)
f(100) = 10000a + 100b => 10000a + 100b = 0 (ii)
5000a + 100b = -50
10000a + 100b = 0
Or, 5000a = 50 => a = 50/5000 = 0.01.
50b = -25 – 2500*0.01 = -25 – 25 => b = -1
Hence, equation of curve is f(x) = 0.01x^2 –x
b) The amount of water that hold by Bunyip reservoir is volume of the reservoir = area *

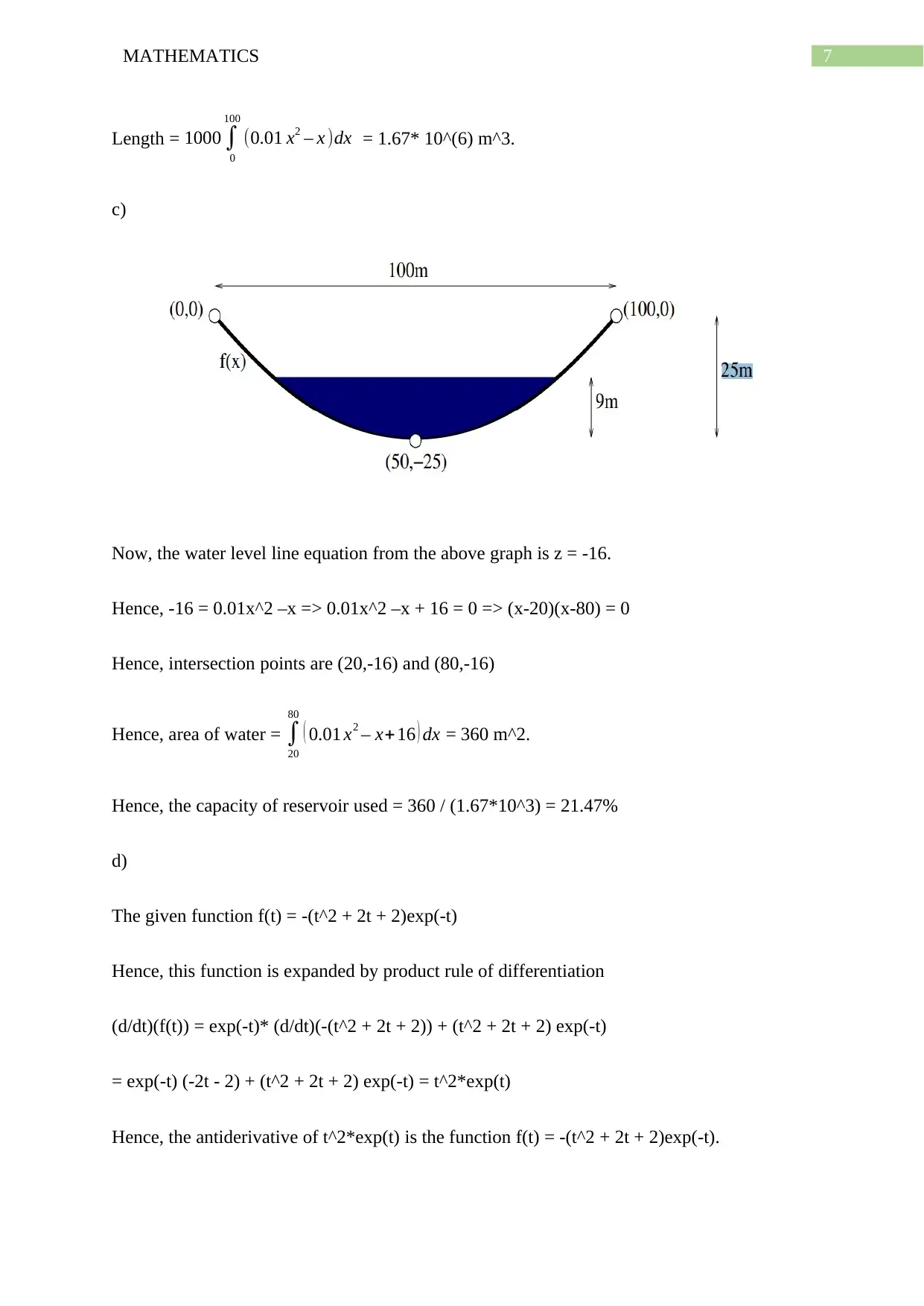
7MATHEMATICS
Length = 1000 ∫
0
100
(0.01 x2 – x )dx = 1.67* 10^(6) m^3.
c)
Now, the water level line equation from the above graph is z = -16.
Hence, -16 = 0.01x^2 –x => 0.01x^2 –x + 16 = 0 => (x-20)(x-80) = 0
Hence, intersection points are (20,-16) and (80,-16)
Hence, area of water = ∫
20
80
( 0.01 x2 – x+16 ) dx = 360 m^2.
Hence, the capacity of reservoir used = 360 / (1.67*10^3) = 21.47%
d)
The given function f(t) = -(t^2 + 2t + 2)exp(-t)
Hence, this function is expanded by product rule of differentiation
(d/dt)(f(t)) = exp(-t)* (d/dt)(-(t^2 + 2t + 2)) + (t^2 + 2t + 2) exp(-t)
= exp(-t) (-2t - 2) + (t^2 + 2t + 2) exp(-t) = t^2*exp(t)
Hence, the antiderivative of t^2*exp(t) is the function f(t) = -(t^2 + 2t + 2)exp(-t).

8MATHEMATICS
e) Now, 1 m^3 = 1000 litres
Now, the empty volume of reservoir = 1.67* 10^(6) – 360*10^3 = 1310000 m^3 = 131*10^7
litres = 1.31 giga-litres
Now, water enters at e^(-t)*t^2 litres per day, where t is the number of days from Sunday.
Hence, dx/dt = e^(-t)*t^2 => x = -(t^2 + 2t + 2)exp(-t) + c, where x is amount of water
Hence, Now, at t= 0 x = 0.36 giga-litres
Hence, 0.36 = c – 2 => c = 2.36
Hence, x = -(t^2 + 2t + 2)exp(-t) + 2.36
Now, a value of t in between 2 and 3 gives amount of water x = 1.31 giga-litres.
Hence, it can be said that the overflow from reservoir will start from some point in the
morning of Thursday.
f) All points under water is expressed by the following relation equation
y = 0.01 x2 – x +16
Where, y is height and x is the breadth of reservoir.
g) All point above water is expressed by the following piecewise defined function.
y = 0.01 x2 – x for all x in [0,20)
= -16 for all x in [20,80]
= 0.01 x2 – x for all x in (80,100]
4.

9MATHEMATICS
Let, the total number of members in Tim Tam Appreciation Society is n and the number of
Tim Tams in each novelty, regular and family packet are x, y and z respectively.
The Tim-Tam consumption table is shown below.
a)
Now, the equations will be
x + 17y + 7z = 9n + 3 (Monday)
2x + 16y +3 = 5(n-1) + 17 (Tuesday)
3x + 4y + 8z +17 = 7(n-2) + 3 (Wednesday)
2y + 18z + 3 = 6*2*(n-5) + 1 (Thursday)
9x + z +1 = 4*(n-12) + 2 (Friday)
b) Now, the equations are converted in AX = B form as given below.
x + 17y + 7z – 9n = 3
2x + 16y -5n = 9
3x + 4y + 8z – 7n = -28
2y + 18z -12n = -62

10MATHEMATICS
9x + z – 4n = -47
Now, as there are 4 unknowns and 5 equations hence, last two equations are added to form
one equation. Now, system of linear equations are
x + 17y + 7z – 9n = 3
2x + 16y -5n = 9
3x + 4y + 8z – 7n = -28
9x + 2y + 19z – 16n = -109
Hence,
[ 1 17 7 −9
2 16 0 −5
3 4 8 −7
9 2 19 −16 ] [ x
y
z
n ] =
[ 3
9
−28
−109 ]
c) Now, Gaussian elimination is applied to reduce the matrix into row-echelon form.
Augmented matrix A =
[ 1 17 7 −9 3
2 16 0 −5 9
3 4 8 −7 −28
9 2 19 −16 −109 ]
=
[ 1 17 7 −9 3
0 −18 −14 13 3
0 −4 7 −13 20 −37
0 −151 −44 65 −136 ]
(By operation R2 = R2 – 2R1, R3 = R3 – 3R1, R4 = R4-9R1)
Now, sequenced operations R2 = R2/-18, R1 = R1 – 17R2, R3 = R3 + 47R2, R4 = R4 +
151R2, R3 = R3 * (9/212), R1 = R1 + (56/9)R3, R2 = R2 – (7/9)R3, R4 = R4 – (661/9)R3

11MATHEMATICS
R4 = R4*(-424/245), R2 = R2 + (111/424)*R4 and finally R3 = R3 + (251/424)*R4 is
performed to obtain the reduced row echelon form given below.
Row-reduced(A) =
[1 0 0 0 9
0 1 0 0 11
0 0 1 0 20
0 0 0 1 37 ]
Hence, comparing x,y,z and n coefficients
x = 9
y = 11
z = 20
n = 37
e) Now, the Tim Tams consumed in each of the weekdays are calculated as given below.
Monday = 9*n = 9*37 = 333 Tim tams
Tuesday = 5*(n-1) = 5*36 = 180 Tim tams
Wednesday = 7*(n-2) = 7*35 = 245 Tim Tams
Thursday = 6*2*(n-5) = 12*32 = 384 Tim Tams
Friday = 4*(n-12) = 4*25 = 100 Tim Tams